一种基于通行优先度规则的城市交通信号自组织控制方法
2018-01-27王安麟孙晓龙钟馥声
王安麟,孙晓龙,钟馥声
(同济大学 机械与能源工程学院,上海 201804)
0 引 言
长久以来,由于人们的交通习惯,城市交通信号的控制都是建立在固定的相位和相序基础之上的,国内对基于实时交通信号控制的相位组合和可变相序的研究较少。国内很多学者把研究的重心放在人工智能上,比如神经网络、模糊控制、强化学习等[1-3]。基于这些算法的交通控制虽然大大提高了通行效率,但是仍然是针对单一相位进行绿时优化,其相位组合和相位顺序是不变的,灵活性差。
国外大量交通信号自组织控制的研究,避免了上述缺陷,其交通信号没有固定的周期和相序。C. GERSHENSON根据各个相位是否超过“阈值”来作为相位获得通行权的依据[4];B. PLACZEK利用时间间隔的微观交通模型来预测各个可能的控制行为的效果,进而选择最佳相位获得通行权[5]。但是上述方法控制参数太多,实施起来比较困难。且不管是人工智能还是自组织控制,他们都孤立的看待每个路口,忽略了周围路口对本地路口控制行为的影响。
较早前作者就对交通信号自组织控制进行了研究,而当时并没有针对相位和相序可变提出规则[6]。笔者正是在此前工作的基础上,针对前人研究的不足,提出了包含通行优先度、交叉口关联度和相位组合的通行优先度规则。最后建立了基于元胞自动机(CA)的城市交通微观模型,并在NetLogo平台上进行了交通仿真。仿真结果表明:此方法降低了路网内车辆的延误时间和停车次数,提高了车辆的平均速度。
1 通行优先度规则
文中的通行优先度规则是在交通信号自组织的体系下,每个交叉口在既定的规则下、依据实时交通量做出自己的决策,没有固定的周期和绿信比。通行优先度规则包含PC规则(相位组合)、QT规则(通行优先度)和IR规则(交叉口关联度)。
1.1 PC规则
相位是连接交叉口时间和空间设计的纽带,合理的相位,不但能够最大限度地适应交叉口空间的配置,而且能够保证交通流在交叉口安全、有效地通过,提高交叉口的通行能力[7]。传统的相位设计是在调查交叉口路面特征以后,根据历史车流数据而定。单一的相位组合只能满足具有特定特征的车流,而无法随着车流特征的改变而改变。因此,笔者提出了PC(phase combination)规则。下面以图1为例进行说明。
图1是一个简单的十字交叉路口,为了方便对相位进行描述,用数字1~8来表示不同方向的车流。
我们假设右转车流不受控,那么每个方向都有直行和左转两股车流。我们可以有下面3种相位组合方案。
第1种方案:(同方向直行+左转)
1—2、3—4、5—6、7—8
第2种方案:(不同方向合流)
1—4、2—7、3—6、5—8
第3种方案:(不同方向相对运行)
1—5、2—6、3—7、4—8
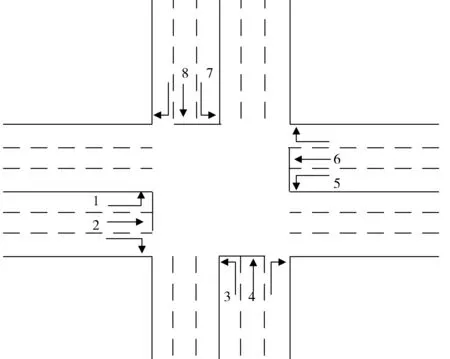
注:数字1— 3— 5— 7表示左转车流;数字2— 4— 6— 8表示直行车流。图1 交叉口车流示意Fig. 1 Traffic flow of intersection
(1)
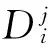
1.2 QT规则
在PC规则中,我们给了相位组合方案的切换规则。在QT规则中,我们将定义相序的切换规则。C. GERSHENSON等人提出了“阈值”的相位切换规则[4],阈值ki为
ki=c×t
(2)
式中:c为时间t内到达红灯的车辆数(不管车辆是运动的还是静止的)。当阈值ki大于某一给定值θ时,那么此相位由红灯转为绿灯。此切换规则的问题在于:当车流量较小时,相位切换不及时;当车流量较大时,相位切换过快。
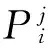
(3)
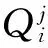
1.3 IR规则
中国路网密度比较大,交叉口之间距离比较近,所以交叉口之间的车流耦合作用也比较强。传统的交通信号控制只考虑交叉口的自身效益,而忽略了对相邻路口的影响。王浩等[8]提出了基本协调单元的概念,即把本地路口、上游路口及它们所包含的路段构成一个子区,进行协调优化。传统理论也认为,上游路口车流量的大小影响本地路口的信号控制,而没有考虑下游路口对本地路口的影响。假如下游路口车辆很多,如果再放行车辆,势必会造成本地交叉路口的堵塞,直接影响其他方向车流的放行。基于此,笔者提出了一个简单有效的交叉口关联度IR(intersections relation)规则,把本地路口与所有相邻的路口关联起来进行决策。
如图2,路口n的车流4是由上游路口n-1的车流1、2、3合流而成,下游路口n+1的车流是由路口n的车流4、5、6合流而成。如果车流7很大,则减缓或暂停上游车流4、5、6的流入。通过这样的机制,本地路口所有相位的通行与否就与所有相邻路口的车流形成了一个关联共同体,能够有效预防拥堵的产生,而不是在拥堵产生时才去缓解拥堵。
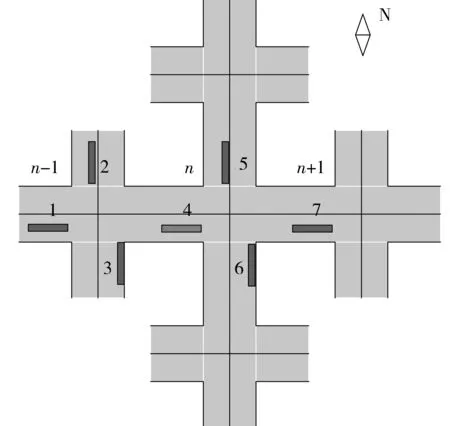
图2 交叉口之间的车流关联Fig. 2 Traffic flow association between intersections
笔者定义交叉口关联度系数k,k的大小影响相位通行优先度的大小,则有
(4)
式中:k的大小取决于相位j所对应的下游路口车流量的大小(比如在图1中,如果车流1、2组合成一个相位,那么此相位对应的下游路口为2个,分别为左转对应的上方路口和直行对应的下方路口),0≤k≤1 。文中给出3个特定值。当相位对应的任何一个下游路口道路占有率达到90%以上时,k=0,那么此相位的通行优先度为0,禁止此相位的车辆流入下游。当相位对应的任何一个下游路口道路占有率小于90%大于60%时,k=0.5,减缓此相位车辆流入下游。当相位对应的下游路口道路占有率都≤60%时,k=1,此相位车辆正常驶入下游。k的取值会在以后的工作中详细加以研究。
2 城市交通模型
城市交通模型是研究交通信号控制的基础,大致分为两类:宏观模型和微观模型。从宏观角度出发,M. J. LIGHTHILL等[9]将交通流近似为连续流体,提出了LWR模型;而I. PRIGOGINE等[10]提出了交通流气动理论模型;从微观角度出发,L. A. PIPES等[11]提出了能够描述车辆驾驶行为的跟驰模型。随着元胞自动机模型(cellular automata,CA)的出现,近些年来,基于CA的城市交通微观模型的研究迎来了一个高峰。
仿真实验采用的正是基于元胞自动机的城市交通微观模型。此前很多学者在研究交通信号自组织控制时,建立的CA路网模型都是单向单车道的,车辆方向分别为由西向东、由北向南(如C. GERSHENSON[4]和J. SEKLARSKI[12]),模型过于简单,相位数太少。为了更加贴近实际,笔者采用双向四车道,每个方向都有直行和左转两个车道,每个车道都是由一维的元胞自动机组成,每个cell有两种状态:被车辆占据或者是空的,如图3为单交叉口城市交通模型图。在每个离散的时间步内,车辆的运动满足以下规则。
2.1 加速
当车辆运动前方的cell是空的,车辆将加速。
vn(t+1)→min[vn(t)+a,vmax]
(5)
式中:a表示加速度的大小,vmax表示车辆最大速度。
2.2 减速
当车辆运动前方的cell被同向车辆占据时,车辆减速,其速度最大可以保持与前方车辆速度相等。
vn(t+1)→min[vn(t)-a,vn+1(t+1)]
(6)
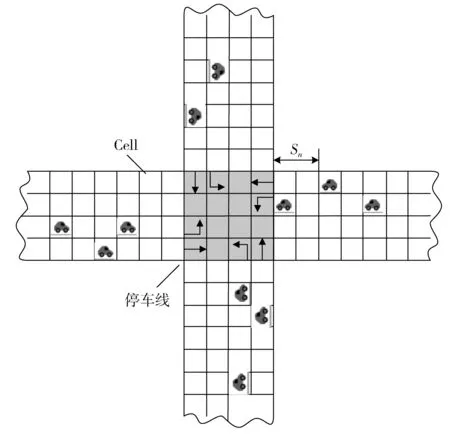
图3 单交叉口城市交通模型Fig. 3 Urban traffic model of single intersection
2.3 刹车
当车辆距离交叉口停车线3个cells,且前方无车辆时,如果信号灯为红色或变为红色,则刹车。
vn(n+1)→min[vn(t)-a,0.5(sn-1)]
(7)
式中:sn表示车辆距离交叉口停车线的cell个数,1≤sn≤3。
2.4 车辆运动
车辆运动方程如下:
xn(t+1)=xn(t)+vn(t+1)
(8)
2.5 随机车道选择
不管是直行车辆还是左转车辆,在其经过交叉口后,随机选择进入下游路段的左转车道的概率为p,进入直行车道的概率则为1-p。
随机车道选择决定了车辆的行驶方向,加速、减速、刹车以及运动方程决定了车辆的行驶状态(速度和加速度)。车辆不管是直行、合流还是分流,都能够平稳有序进行,不会发生碰撞。CA模型的仿真参数会在后面的仿真模型里给出。
3 仿真实验和结果分析
3.1 仿真模型
NetLogo 是一个用来对自然和社会现象进行仿真的可编程建模环境,特别适合对随时间演化的复杂系统进行建模。为验证该自组织方法的有效性,在此平台上进行了建模仿真。
笔者基于CA模型构建了4×4共16个交叉口的交通路网模型。在仿真实验开始时,系统初始化车辆数为16,此后每隔150个时间步车辆增加16,以观测在不同饱和度情况下算法的控制效果。车辆在边界驶出时,会在相反方向的边界处重新驶入,所以整个路网的车辆数不会减少。车辆长度为7.5 m(包括前后安全距离),相邻两个交叉口之间的距离为240 m,车辆加速度a=0.01,最大速度vmax为1(即一个tick车辆最大行驶距离为一个cell),概率p=0.3,仿真步数为8 000。仿真程序里2个时间步相当于真实环境的1 s。笔者以路网内车辆的平均延误时间、平均速度和停车率作为系统性能的评价指标,仿真界面如图4。
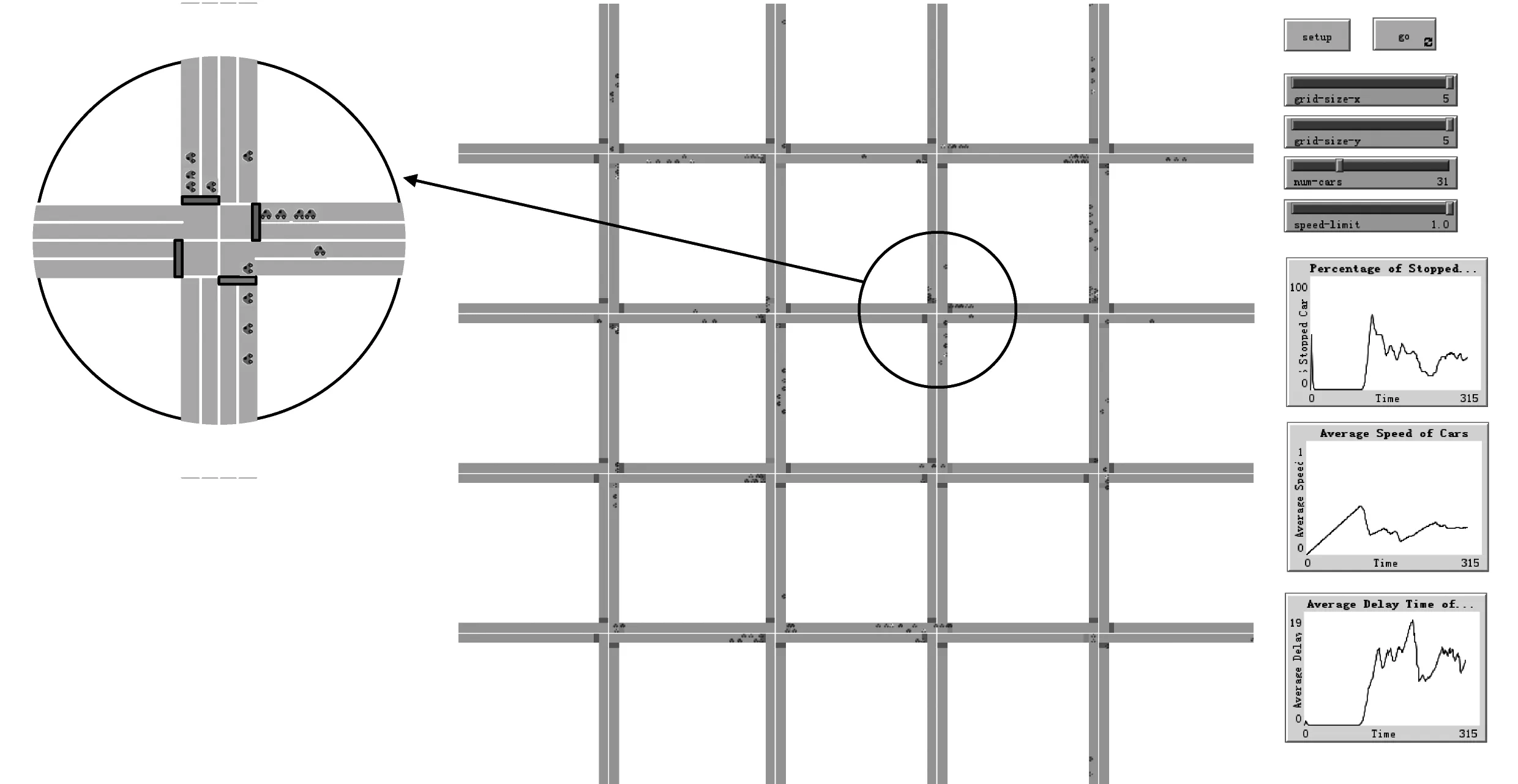
图4 仿真界面Fig. 4 Simulation interface
3.2 通行优先度规则在仿真平台里的实现
3.2.1 PC规则的实现
每隔5 min(120个时间步),比较公式(1)中各个方案车流差度和的计算结果,选择最小值为新的相位组合方案。
3.2.2 QT规则,IR规则的实现
因为IR规则实际上包含了QT规则,所以只考虑IR规则的实现。笔者取最小绿灯时间为10 s,最大绿灯时间100 s,在PC规则的前提下,按照式(4)计算各个相位的通行优先度,通行优先度最大的相位将获得通行权。同时,为了不打断正在通行的车流队列,在未达到最大绿灯时,如果停车线所在cell被车辆占据,那么此相位将获得绿灯延时时间5 s(每隔5 s滚动判断一次)。整个相位切换流程如图5。
3.3 实验对比
在模型参数都相同的情况下,将文中自组织的方法与定时控制和感应控制进行了性能对比。各个控制策略描述见表1。 定时控制和感应控制的相位组合方案为章节1中PC规则的第1种方案。定时控制各个相位时长为35 s,周期时长140 s。感应控制的最小绿灯时间为10 s,最大绿灯时间100 s,绿灯延时时间5 s,其相位切换流程大致和图5一样,只是在切换相位上,自组织的方法是根据QT、IR规则,相序是可变的,感应控制是按照PC规则方案一中的相位顺序直接切换,相序是不变的。
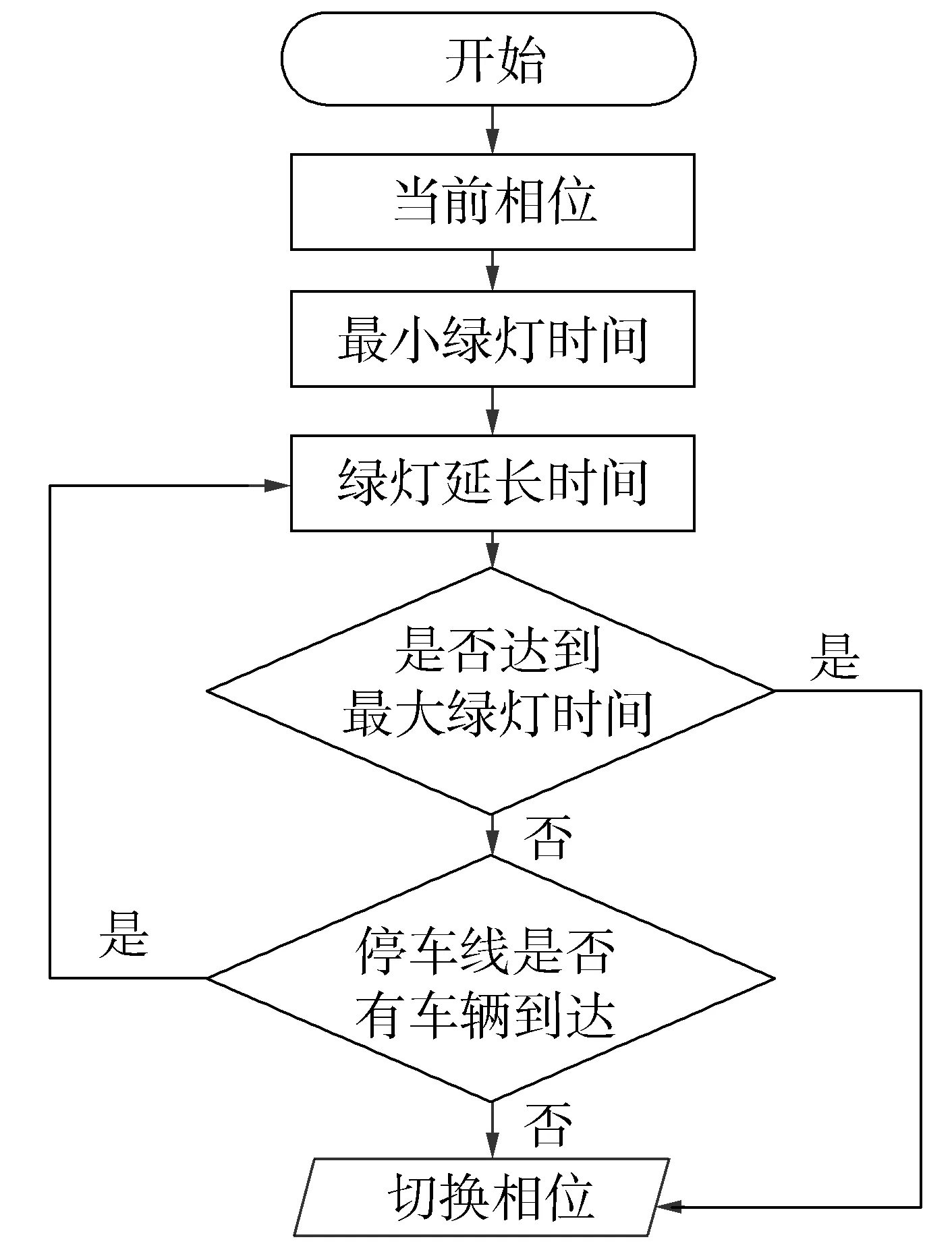
图5 相位切换流程Fig. 5 Phase switching process

控制策略1定时控制绿信比,相位转换时间和周期时长都保持一定数值固定不变2感应控制在最小绿时、最大绿时限制下,根据车辆到达情况决定绿灯延时或关闭,相位和相序不变3自组织方法本文提出的相序可变的交通信号自组织控制方法
3.4 结果分析
表2是整个仿真过程速度、停车率和平均延误时间的对比。基于通行优先度规则的自组织控制算法在3个评价指标上都明显优于其他两种控制方法。
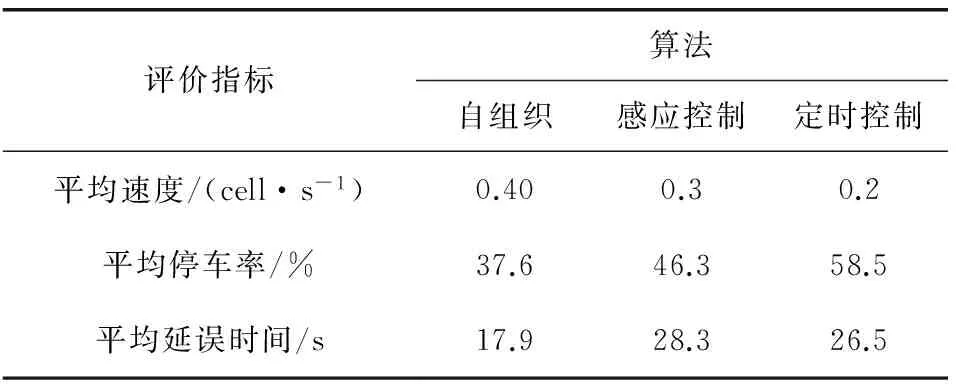
表2 三种控制算法效果比较Table 2 Comparison of the effect of three control algorithms
图6分别是车辆平均速度、停车率和平均延误时间随着时间(饱和度由低到高)的演化图。在低饱和度时,感应控制在车辆平均速度和停车率上表现和自组织方法相当,明显优于定时控制。但是随着车辆数的增加,感应控制的平均延误时间增加幅度明显大于定时控制和自组织控制。这是由于感应控制对单个相位而言达到了最优控制,但是相序是固定不变的,车辆较多、等待时间较长的相位车辆得不到及时疏通,造成平均延误时间大幅增加。
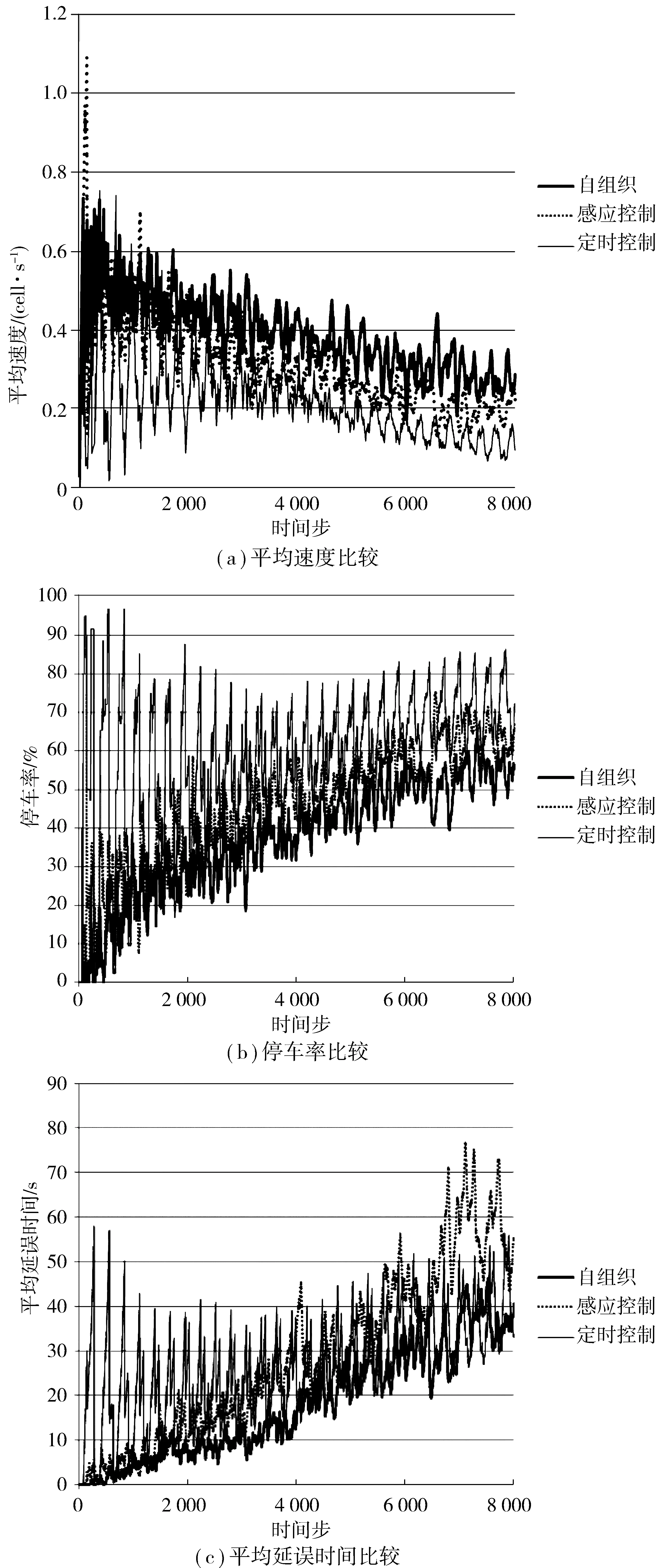
图6 实验数据分析Fig. 6 Experimental data analysis
从演化图中也可以发现,定时控制方法在各个评价指标中波动比较大,这是由于交叉口之间没有对相位差进行优化所致。定时控制虽然在低饱和度和中等饱和度控制效果较差,但是在高饱和度时,其控制效果和感应控制相当,在平均延误时间方面,甚至比感应控制还要好。这是由于高饱和度时,定时控制的周期循环相对较快,不同方向的车流都得到了通行。而感应控制大都在最大绿时切换相位,当各个相位车流量不均衡的情况下,更容易导致路口堵塞。自组织方法由于考虑了车流均衡(PC规则)和相序可变(QT规则),所以能让交叉口在相同时间内通过更多的车辆,均衡了交叉口车流。同时,因为考虑了路口之间的耦合作用(IR规则),所以在整个仿真过程当中,交叉口没有出现堵塞的情况。
总之,采用笔者提出的自组织控制方法,不管在低饱和度、中等饱和度和高饱和度下,都达到了良好的控制效果,具有良好的鲁棒性。
4 结 语
提出的基于通行优先度规则的城市交通信号自组织控制方法,避免了传统固定相位、单一相序对底层的“束缚”和由于计算量大而难以实时控制的缺陷,充分考虑了车流均衡、相序可变以及交叉口之间耦合作用的影响,保证了较高的通行效率,有效提高了路段内车辆的平均速度,减少了停车等待次数,降低了延误时间。文章是对交通信号自组织控制方法的一种理论性探索,对新一代智能交通控制装备与系统的工程化具有一定的指导性意义。
[1] 曾松林.城市单交叉路口交通信号的控制方法研究[D].成都:西南交通大学,2013.
ZENG Songlin.StudyonTrafficSignalControlMethodforUrbanSingleIntersection[D].Chengdu:Southwest Jiaotong University,2013.
[2] 曹洁,李振宸,任冰.基于神经网络模糊控制的单交叉口信号控制[J].兰州理工大学学报,2010,36(1):86-90.
CAO Jie,LI Zhenchen,REN Bing.Single intersection signal control based on fuzzy neural network control[J].JournalofLanzhouUniversityofTechnology,2010,36(1):86-90.
[3] 伦立宝.基于强化学习的城市交通信号控制方法研究[D].西安:西安电子科技大学,2013.
LUN Libao.ResearchonReinforcementLearning-basedUrbanTrafficLightControl[D].Xi’an:Xidian University,2013.
[4] GERSHENSON C.Self-organizing traffic lights[J].ComplexSystems,2005,16:29-53.
[5] PLACZEK B.A self-organizing system for urban traffic control based on predictive interval microscopic model[J].EngineeringApplicationsofArtificialIntelligence,2014,34(3):75-84.
[6] JUNHUA Wei,ANLIN Wang,NIANCI Du.Study of self-organizing control of traffic signals in an urban network based on cellular automata[J].IEEETransactionsonVehicularTechnology,2005,54(2):744-748.
[7] 冯胜利.基于多相位变相序的单交叉口信号配时优化研究[D].兰州:兰州交通大学,2014.
FENG Shengli.TheResearchonSignalTimingOptimizationofIsolatedIntersectionBasedonMultiphaseandVariablePhaseSequence[D].Lanzhou:Lanzhou Jiaotong University,2014.
[8] 王浩,时柏营,杨晓光.自组织式交通信号协调控制模型[J].计算机测量与控制,2012,20(11):2979-2982.
WANG Hao,SHI Baiying,YANG Xiaoguang.Self-organizing model of traffic signal coordinated control[J].ComputerMeasurement&Control,2012,20(11):2979-2982.
[9] LIGHTHILL M J,WHITHAM G B.A theory of traffic flow on long crowded roads[J].MathematicalandPhysicalSciences,1955,229(1178):317-345.
[10] PRIGOGINE I,HERMAN R.KineticTheoryofVehicularTraffic[R].New York:Ecsevier,1971.
[11] PIPES L A.An operational analysis of traffic dynamics[J].JournalofAppliedPhysics,1953,24(3):274-281.
[12] SEKLARSKI J.Cellular automata model of self-organizing traffic control in urban networks[J].BulletinofthePolishAcademyofSciences:TechnicalSciences,2010,58(3):435- 441.
