基于结构方程的通勤廊道停车换乘行为建模分析
2018-01-27向红艳何素贞
向红艳,何素贞,徐 韬
(重庆交通大学 交通运输学院,重庆 400074)
0 引 言
停车换乘(P & R)出行行为是交通需求管理在静态交通领域的一种重要应用。能否准确把握P & R 选择行为关系到交通建设、交通政策制定及交通管理的准确性和科学性,并直接影响城市交通系统的结构及系统整体效率发挥。
随着城市规模扩大,居住区与工作区愈渐分离,通勤出行距离不断增加,形成了较为固定的通勤廊道。通常,通勤廊道的出行方式可分为:公共交通、小汽车、P & R。P & R是提高廊道通行速度,缓解城市中心区交通拥堵、停车困难等问题的有效措施。因此,通勤廊道的P & R行为,将成为研究的重点。当出行者做出出行方式决策时,除可直接观测因素,不可直接观测因素也对出行决策结果产生效应。研究各种影响因素的关系及潜在因素,对选择结果影响机理和全面分析P & R选择行为具有重要意义。
学界运用Logit模型、随机网络模型、决策树模型等研究了P & R行为特征及其影响因素[1-9]。D.HESS[1]建立了工作出行方式选择多项Logit模型,分析了停车费用对通勤交通方式的影响;云美萍等[2]针对道路交通通畅、堵塞这2种状态分别建立了是否停车换乘的二项Logit模型,指出通勤者在道路通畅时更关注出行费用,堵塞时更关注出行时耗和舒适性;A.R.HOLE[3]研究了通勤者收入、目的地停车位供给对P & R出行行为的影响;范文博等[4]建立了随机多方式交通网络均衡模型,提出交通信息对P & R行为的影响,并指出信息特性中的信息质量对P & R行为有较大影响。上述学者从不同角度研究了P & R出行行为,并提出多种影响因素。
在P & R选择行为中,为解释一组潜变量之间、显变量与潜变量之间的因果关系,可能涉及到很多测量变量,通常会形成复杂的层次关系结构,无法使用传统的回归分析方法求解,需要更精确地路径分析工具,并能对模型进行参数估计和相关检验,而结构方程模型(structural equation model,SEM)正适合处理这类问题。SEM模型能很好地分析一个或多个自变量与一个或多个因变量之间的一组相互关系,而自变量和因变量既可以是连续的,也可以是离散的,并可对不同的理论模型进行评价分析,是多元数据统计的重要工具之一,已被广泛运用于心理学、社会科学等学科。但一直以来,SEM在交通出行行为领域的应用较少[10-15]。
鉴于以上分析,笔者以重庆市城市居民P & R问卷调查数据为基础,通过引入SEM模型,选取个人属性、信息需求偏好及停车换乘设施服务水平作为外源潜变量,出行目的、出发时刻、出行方式及出行强度作为内生潜变量,对潜变量间关系及潜变量与相对应观察变量间的关系进行了进一步研究。由于P & R出行模式中大多为小汽车+轨道交通的停车换乘模式,因此笔者的研究对象为小汽车拥有者基于轨道交通的通勤廊道P & R出行行为。
1 结构方程模型
结构方程模型(SEM)是一种基于变量的协方差矩阵来分析变量之间关系的统计方法。该模型整合了因素分析与路径分析两种统计方法。包含直接观测潜在变量、可直接观测显性变量及干扰或误差变量。通过检验此3种变量之间的关系,进而获得自变量对因变量影响的直接效果、间接效果或总效果[16]。
完整的SEM模型包括测量模型(measurement model)和结构模型(structure model)两个基本模型。
测量方程:
y=Λyη+ε
(1)
x=Λxξ+δ
(2)
式中:y为内生显变量组成的向量;x为外源显变量组成的向量;Λy为y在η上的因子负荷矩阵;Λx为x在ξ上的因子负荷矩阵;ε为内生显变量的误差项;δ为外源显变量的误差项。
结构方程:
η=Bη+Γξ+ζ
(3)
式中:η为内生潜变量;ξ为外源潜变量;B为系数矩阵,代表内生潜变量η之间的关系;Γ为系数矩阵,代表外源潜变量ξ对内生潜变量η的影响;ζ为结构方程的残差项,反映了η在方程中未能被解释的部分。
测量模型与结构模型关系如图1。图1中:结构方程模型含有3个测量模型和1个结构模型;单向箭头表示两个变量间的因果关系,由“因”指向“果”,由外因潜变量指向内因潜变量;双向箭头表示两个变量间的相关关系,两者间不存在因果关系。
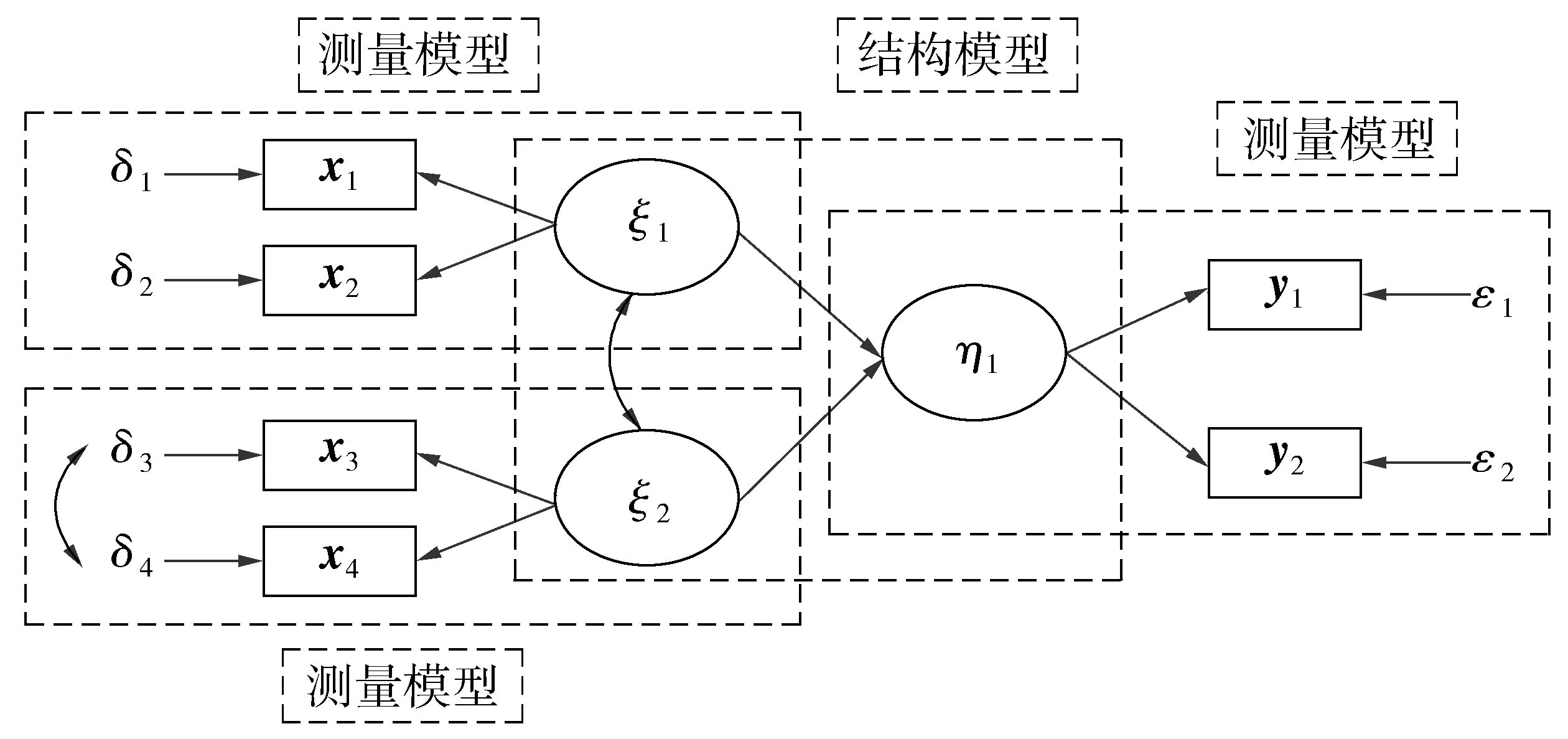
图1 结构模型示意Fig. 1 Schematic diagram of SEM
2 居民停车换乘行为结构方程模型
2.1 交通调查
2.1.1 数据调查与检验
结构方程模型采用协方差建模时,为保证模型有更精确地拟合效果,所需样本数至少是测量变量的10倍以上[17]。为全面地对通勤廊道的P & R出行行为进行研究,借鉴以往研究,问卷中共设置25个观察变量。
笔者选取重庆市通勤廊道的P & R停车场,采用现场发放问卷、现场回收的方法进行了调查。除去不认真作答、问项未完全作答及连续选择极端值大于5个的样本,最终得到456份有效问卷,作为模型原始数据。
分析调查数据前,使用式(4)计算问卷调查中的克朗巴哈系数:
(4)
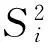
经计算,问卷调查中的克朗巴哈系数α=0.86,表明问卷设计具有良好信度[18]。
2.1.2 探索性因素分析
笔者采用主成分分析法进行因子分析。将456份调查数据输入SPSS软件中进行因子分析,以特征根大于1、因子载荷大于0.5为标准,经过旋转后,提取了7个因子:个人属性、信息需求偏好、P & R设施服务水平、出行目的、出发时刻、出行方式、出行强度。结果显示:各变量的因子载荷都大于0.6,即因子对变异量解释程度较高,说明结果表明变量选取较科学、合理。旋转后的荷载矩阵具体如表1。

表1 观察变量探索性因子分析结果Table 1 Exploratory factor analysis results of observation variables
注:X1为性别、X2为年龄、X3为月收入、X4为学历、X5为驾龄、X6为路况状态信息、X7为路径导航信息、X8为交通管制信息、X9为停车信息、X10为事故信息、X11为换乘优惠、X12为停车位供给、X13为停车信息服务、Y1为通勤出行、Y2为非通勤出行、Y3为出发时刻为07:00—09:00、Y4为出发时刻为09:00—14:00、Y5为出发时刻为14:00—17:00、Y6为出发时刻为17:00—19:00、Y7为出发时刻为19:00—22:00、Y8为小汽车、Y9为公共交通、Y10为小汽车换乘轨道交通、Y11为出行距离、Y12为出行时间。
2.2 变量选取
笔者对模型作如下假设:① 个人属性与信息需求偏好有相关关系;② 个人属性、信息需求偏好、P & R 设施服务水平对出行目的、出发时刻、出行方式、出行强度产生直接影响。为简化模型,调高模型适配度,最终确定个人属性、信息需求偏好和换乘设施服务水平为外源潜在变量,出行目的、出发时刻、出行方式和出行强度为内生潜在变量。各潜变量及对应观察变量特征具体如表2、3。

表2 结构方程外源变量解释Table 2 Exogenous variable explanation for SEM
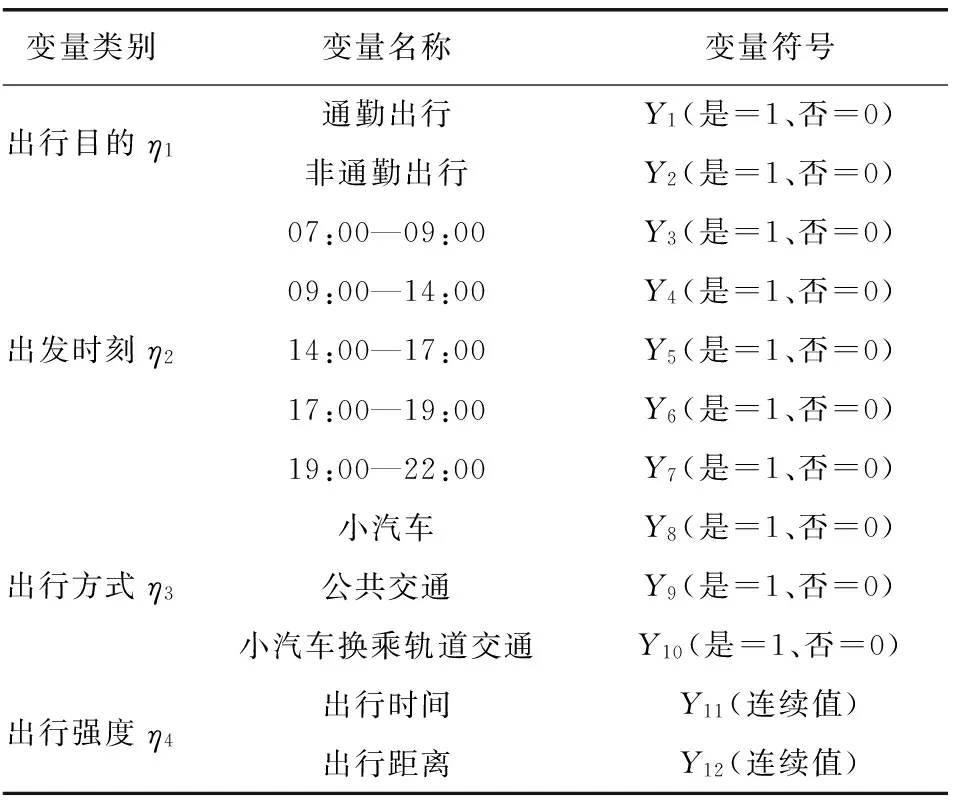
表3 结构方程内生变量解释Table 3 Endogenous variable explanation for SEM
2.3 概念模型
基于轨道交通的P & R出行行为研究可由出行者个人属性、信息需求偏好及换乘设施服务水平组成的外源潜变量,出行目的、出发时刻、出行方式及出行强度组成的内生潜变量之间的关系与各观察变量间的关系表示。根据现有研究成果,构建结构方程概念模型,具体如图2。
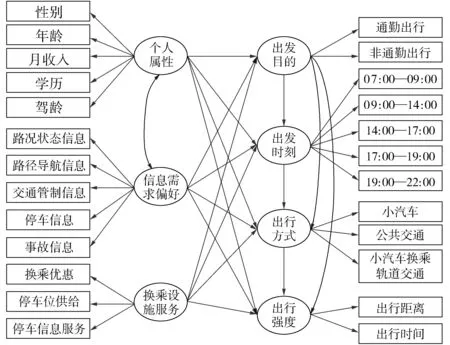
图2 模型示意Fig. 2 Schematic diagram of model
3 模型标定及评价
3.1 模型标定
运用SPSS软件建立数据库,并以此为基础导入LISREL8.72中进行分析,构建结构方程模型,采取最大似然法(maximum likelihood,ML)进行估算。模型的标定结果如图3。

图3 采用LISREL分析得到的P & R出行行为分析路径Fig. 3 Path diagram of rail park-and-ride behaviors obtained by LISREL analysis
结合表2、3和图3对各变量进行分析,具体如下:
1) 个人属性路径表明:收入和驾龄是主要影响因素,效应值分别为0.51、0.42,即低收入和驾龄较低的出行者更倾向于停车换乘。
2) 信息需求偏好路径表明:路况状态信息、事故信息及停车信息对P & R出行行为影响较显著,效应值分别为0.80、0.72、0.60。当中心区道路拥挤、停车供给不足时,居民选择P & R出行方式概率较大。
3) 换乘设施路径表明:提高P & R处停车位供给及提升停车信息服务水平是吸引居民选择P & R的强有力措施,效应值分别为0.62、0.51。
4) 出行目的路径表明:通勤廊道上选择P & R的出行者大多是通勤者。
5) 出发时刻路径表明:当在07:00—9:00与17:00—19:00这两个时段时,居民选择P & R比率较高,即早高峰和晚高峰时段居民选择P & R出行方式的比例较大,平峰时段P & R出行方式使用率较低。
6) 结构模型中外源潜变量ξ1、ξ2、ξ3和内生潜变量η1、η2、η3、η4之间的路径表明:个人属性ξ1对出行方式影响较显著,效应值为0.56;信息需求偏好ξ2对出行方式和出发时刻具有重要影响,效应值分别为0.57、0.35;换乘设施服务ξ3对出行方式具有显著影响,效应值为0.61。
7) 观测变量对内生潜变量的间接影响可通过外生潜变量各观测变量的负荷系数乘以路径系数得到。其中:在个人属性ξ1中,性别x1对居民P & R出行行为影响较弱;在信息需求偏好ξ2中,路径导航信息x7对居民P & R出行行为影响不显著;在换乘设施服务ξ3中,换乘优惠x11对居民方式决策影响较低。
3.2 模型评价
模型适配度是指观测资料与假设模型之间一致性程度。结构方程模型适配度检验可根据用于验证的样本规模、数据特征及假设条件选择相应的指标[19]。笔者选取6个关键特征指标,衡量模型的拟合精度,如表4。结果表明:调查数据与模型能够较好适配。
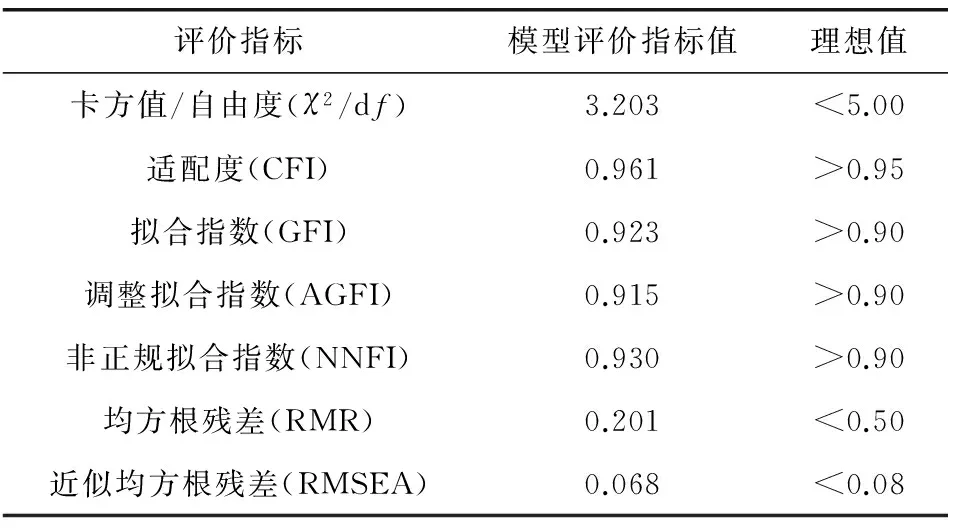
表4 模型拟合优度评价Table 4 Grade evaluation of model fitting
4 结 论
通勤出行在时间和空间上具有较强的规律性,通勤廊道上的出行特征与通勤者属性、偏好有关。P & R 出行可有效降低小汽车出行,提升高容量、低能耗的公共交通出行,从而提升通勤廊道服务水平,缓解交通拥堵。结构方程模型具有反应信息全面、模型解释能力强、可移植性高等优点,为P & R出行行为研究提供了全新的思路。
笔者基于结构方程模型(SEM),选取个人属性、信息需求偏好及停车换乘设施服务水平作为外源潜变量,出行目的、出发时刻、出行方式及出行强度作为内生潜变量,对通勤廊道上的P & R出行行为进行了进一步的研究。结果表明:路况状态信息、事故信息及停车信息对P & R出行行为影响效应较显著;出发目的具有最高的优先级别,对出发时刻、出行方式及出行强度产生影响;早高峰和晚高峰时段居民选择P & R出行方式的比例较大;P & R处停车位供给水平、停车信息服务对P & R出行行为影响效应较显著。研究成果可为通勤廊道的交通需求管理提供参考,对于提高P & R系统的利用率,优化出行结构具有重要的意义。此外,结构方程模型在形式上具有很大灵活性,可通过增加变量或采用不同路径关系进行优化,力求更加准确地反应P & R出行特性。
[1] HESS D.Effect of free parking on commuter mode choice:evidence from travel diary data[J].JournaloftheTransportationResearchRecord,2001,1753(1):35- 42.
[2] 云美萍,刘贤玮,陈震寰,等.通勤出行中停车换乘选择行为分析与建模[J].同济大学学报(自然科学版),2012,40(12):1825-1830.
YUN Meiping,LIU Xianwei,CHEN Zhenhuan,et al.Analysis and modeling of park and ride choice behavior in commuting travel[J].JournalofTongjiUniversity(NaturalScienceEdition),2012,40(12):1825-1830.
[3] HOLE A R.Forecasting the demand for an employee park and ride service using commuters’ stated choices[J].TransportPolicy,2004,11(4):355-362.
[4] 范文博,蒋葛夫.信息作用下随机多方式网络停车换乘行为[J].西南交通大学学报,2008,43(4):524-530.
FAN Wenbo,JIANG Gefu.Park and ride behavior in stochastic multimodal network under ATIS[J].JournalofSouthwestJiaotongUniversity,2008,43(4):524-530.
[5] MOLIN E,BOS I.Exploringheterogeneityinparkandridepreferences:Alatentclassmode[C].Transportation Research Board,Washington DC:National Academy of Sciences,2009.
[6] 王晓磊.面向停车换乘的城市通勤廊道交通方式选择模型研究[D].北京:北京交通大学,2012.
WANG Xiaolei.AnalysisofTransportationModalChoiceModelforMetropolitanCommutingCorridorsOrientatedP&RCombinations[D].Beijing:Beijing Jiaotong University,2012.
[7] 秦焕美,关宏志,龙雪琴.基于决策过程的停车换乘行为研究[J].武汉理工大学学报(交通科学与工程版),2014,38(5):1002-1005.
QIN Huanmei,GUAN Hongzhi,LONG Xueqin.Study on the park and ride behavior based on decision process[J].JournalofWuhanUniversityofTechnology(TransportationScience&Engineering),2014,38(5):1002-1005.
[8] 罗琼.山地组团城市停车换乘方案评价方法[J].重庆交通大学学报(自然科学版),2012,31(增刊1):583-585.
LUO Qiong.Evaluation on park and ride scheme in mountain group city[J].JournalofChongqingJiaotongUniversity(NaturalScience),2012,31(Sup1):583-585.
[9] 惠英,杨飞.英国停车换乘交通对策的实践与借鉴[J].重庆交通大学学报(自然科学版),2008,27(6):1120-1123.
HUI Ying,YANG Fei.Traffic policy of P & R in England and its significance as reference[J].JournalofChongqingJiaotongUniversity(NaturalScience),2008,27(6):1120-1123.
[10] 侯杰泰,温忠麟,成子娟.结构方程模型及其应用[M].北京:教育科学出版社,2004.
HOU Jietai,WEN Zhonglin,CHENG Zijuan.StructuralEquationModelandItsApplications[M].Beijing:Educational Science Press,2004.
[11] 莫一魁,苏永云,沈旅欧.基于结构方程的小汽车驾驶员信息偏好分析[J].系统工程,2009,27(8):85-89.
MO Yikui,SU Yongyun,SHEN Lv’ou.Analysis of car drivers’ preference for traffic information based on structural equation modeling[J].SystemsEngineering,2009,27(8):85-89.
[12] 赵昕,关宏志,巩丽媛.基于结构方程的家庭假日外出活动关联性分析[J].交通运输系统工程与信息,2011,11(4):85-90.
ZHAO Xin,GUAN Hongzhi,GONG Liyuan.Modeling correlation of family holiday activities based on structural equation model[J].JournalofTransportationSystemsEngineeringandInformationTechnology,2011,11(4):85-90.
[13] 魏雪梅,戢晓峰,陈方.基于SEM的驾驶员出行信息搜寻行为分析[J].交通运输系统工程与信息,2012,12(3):174-179.
WEI Xuemei,JI Xiaofeng,CHEN Fang.Drivers’ travel information searching behavior study with structural equation modeling[J].JournalofTransportationSystemsEngineeringandInformationTechnology,2012,12(3):174-179.
[14] 陈坚,晏启鹏,杨飞,等.出行方式选择行为的SEM-Logit整合模型[J].华南理工大学学报(自然科学版),2013,41(2):51-57.
CHEN Jian,YAN Qipeng,YANG Fei,et al.SEM-Logit integration model of travel mode choice behaviors[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition),2013,41(2):51-57.
[15] 朱顺应,吴俣,王红,等.轨道交通乘客满意度不确定性预测与分析[J].重庆交通大学学报(自然科学版),2015,34(6):150-155.
ZHU Shunying,WU Yu,WANG Hong,et al.Uncertainty prediction and analysis on rail passenger satisfaction[J].JournalofChongqingJiaotongUniversity(NaturalScience),2015,34(6):150-155.
[16] 黄芳铭.结构方程模式:理论与应用[M].北京:中国税务出版社,2005.
HUANG Fangming.StructuralEquationModeling:TheoryandApplications[M].Beijing:China Taxation Publishing House,2005.
[17] 戢晓峰,魏雪梅,陈方.基于结构方程模型的公共交通系统公平性评估——以昆明市为例[J].公路交通科技,2013,30(1):126-132.
JI Xiaofeng,WEI Xuemei,CHEN Fang.Evaluation of public transport system equity based on structure equation model:taking Kunming as an example[J].JournalofHighwayandTransportationResearchandDevelopment,2013,30(1):126-132.
[18] NUNNALLY J C.PsychometricTheory[M].New York:McGraw-Hill,1978.
[19] 李琳.城市老年人出行行为及其影响机理研究[D].昆明:昆明理工大学,2014.
LI Lin.StudyonTravelBehaviorandInfluenceMechanismofUrbanElderly[D].Kunming:Kunming University of Science and Technology,2014.
