基于FPGA架构的可变点FFT处理器设计与实现

才 华, 陈广秋, 刘广文, 耿振野, 杜兆圣

(长春理工大学 电子信息工程学院, 长春 130022)

快速Fourier变换(FFT)作为一种有效计算离散Fourier变换(DFT)的方法, 在通信、 滤波及数字谱分析等领域应用广泛. 利用现场可编程门阵列(FPGA)可设计FFT处理器的硬件架构[1].

随着FFT算法的不断完善, 在基-2FFT算法[2]的基础上, 文献[3-6]又提出了基-4、 基-8和基-16固定基以及分裂基等算法. 随着基数r的增加, 算法分解级数逐渐减少, 所需运算量(乘法和加法)也逐渐减少, 但其算法控制的复杂度增大. 由于可实现的点数受到限制, 因此需引进混合基算法兼顾FFT的运算量和复杂度[7].

常用的FFT处理器硬件结构有4种[8]： 顺序结构、 流水线结构、 并行结构和阵列结构. 其中顺序结构运算速度慢, 实时性差； 流水线结构比顺序结构的运算速度提高了logrN倍(其中：N为序列点数；r为基数), 所需的硬件资源有所增加； 阵列结构的运算速度最快, 但所需硬件资源和功耗也最大. 由于流水线结构包含多个独立的蝶形运算单元, 每个单元负责一级蝶形运算, 各级蝶形运算单元间采用流水线方式进行工作, 通过增减结构中蝶形运算单元可实现不同点数序列的FFT, 此外流水线结构还具有芯片面积小、 功耗低以及高数据吞吐量等优点, 因此可采用流水线结构处理硬件资源与处理速度间的关系.

正交频分多址技术(OFDMA)是基于正交频分复用技术(OFDM)的新一代无线接入技术, 在IEEE802.16e物理层标准中, 不同带宽的OFDMA系统采用的FFT点数不同, 如3 M带宽采用256点, 10 M带宽采用1 024点, 20 M带宽采用2 048点等[9-10]. 本文利用FPGA硬件架构, 采用优化的基-4/2混合基分解算法及流水线硬件结构实现可变点FFT处理器的设计, 并将其应用于OFMDA系统中.

1 按频率抽取基-2/4混合基算法原理

1.1 按频率抽取基-2FFT算法原理

设序列点数N=2L(L为整数), 按频率抽取(DIF)基-2FFT算法将输入x(n)按n的顺序分为前后两部分, 将结果X(k)按k的奇偶进行分组[11-12]. 其中

(1)

按k的奇偶性, 将X(k)划分为

(2)

图1 DIF基-2蝶形运算单元Fig.1 Radix-2 DIF butterfly operation unit

由式(2)可得DIF基-2蝶形运算单元, 如图1所示.

1.2 按频率抽取基-4FFT算法原理

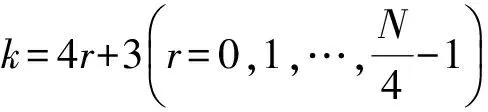
(3)

对X(k)进行分组

(4)

由式(4)可得DIF基-4蝶形运算单元, 如图2所示. 由图2可见, 基-4比基-2蝶形运算复杂, 结构差别较大, 规律性较差, 不适合硬件实现混合基运算, 因此需对上述算法进行优化. 将式(4)中的序列重新分组, 可得优化的DIF基-4FFT算法为

(5)

由式(5)可得优化后的DIF基-4蝶形计算单元, 如图3所示.

图2 传统DIF基-4蝶形运算单元Fig.2 Traditional radix-4 DIF butterfly operation unit

图3 优化后的DIF基-4蝶形运算单元Fig.3 Optimized radix-4 DIF butterfly operation unit

通过计算可知, 优化后的DIF基-4蝶形运算比传统的DIF基-4蝶形运算可减少4个复数加法运算, 其结构与DIF基-2蝶形结构相同, 信号流图具有较强的规律性, 适合硬件实现混合基运算. 图4为优化后N=16的DIF基-4FFT流图.

图4 优化后的DIF基-4FFT流图(N=16)Fig.4 Flow graph of optimized radix-4 DIF FFT (N=16)

由图4可见, 优化后DIF基-4FFT与DIF基-2FFT的各级流图在结构形式上一致, 仅旋转因子不同.

2 混合基FFT算法原理

N点DFT的计算表达式为

(6)

其中N=r1r2…rL为复合数, 按整数的多基多进制表示形式, 式(6)中的n和k可分别表示为

(7)

其中:ni=0,1,…,rL-i-1;ki=0,1,…,ri+1-1,i=0,1,…,L-1. 将式(7)中n和k的值代入式(6)可得

(8)

由式(8)可知, 当满足r1=r2=…=rL-1=rc时, 可将N点DFT分解为(L-1)个基-rcFFT及一个基-rLFFT级联的形式, 从而缩短完成DFT运算所需时间, 并解决基-rcFFT算法无法实现rc非整数次幂DFT算法的问题, 因此本文提出的可变点FFT算法可将DIF基-4和基-2进行级联计算, 且优化后的DIF基-4与基-2算法具有相同蝶形单元结构, 更适合硬件实现混合基运算[13-14].

3 可变点FFT处理器的硬件架构设计及仿真和验证

3.1 FFT处理器流水线结构

基-2或基-4FFT处理器主要有4种流水线结构[15-16], 分别为基-2多路延时转换(R2MDC)结构、 基-2单路延时反馈(R2SDF)结构、 基-4单路延时反馈(R4SDF)结构与基4多路延时转换(R4MDC)结构. R2SDF和R4SDF比R2MDC和R4MDC能更有效利用存储器, R4SDF比R2SDF能更有效利用乘法器, 但R2SDF比R4SDF具有更简单的蝶形结构及更低的控制复杂度. 在混合基算法中, 基-2FFT流水线结构采用R2SDF结构, 优化后的基-4FFT流水线结构采用改进的R2SDF结构, 称为基-22单路延时反馈(R22SDF)结构. 以16点FFT为例, R2SDF结构如图5所示.

图5 R2SDF结构(N=16)Fig.5 Structure of R2SDF (N=16)

首先将输入数据分成上下两部分, 上半部分数据串行输入第一级延时缓存器中, 下半部分第一个数据与缓存单元中的第一个数据送入第一级基-2蝶形单元(数据点间距为N/2)进行运算, 将二者之和送到下一级运算单元, 二者之差送到本级的延时缓存器中, 覆盖第一个数据, 对所有数据依次进行上述处理, 可得第一级蝶形运算的全部结果, 结果的上半部分依次送入下一级继续计算, 下半部分依次存入本级的延时缓存单元； 对进入第二级基-2蝶形运算单元的数据也分为上下两部分, 上半部分数据串行输入第二级延时缓存器中, 下半部分第一个数据与缓存单元中的第一个数据送入第二级基-2蝶形单元进行运算(数据点间距为N/4), 各级基-2蝶形运算单元均采用相同的处理机制, 从而保证各级数据流的连续性, 最后得到计算结果.

由图1和图2可知, 优化后的基-4蝶形单元与基-2蝶形单元具有相同结构, 仅在BF2Ⅰ阶段需乘以一个-j, 对R2SDF结构进行改进得到优化后的基-4FFT流水线单路延时反馈结构, 其数据流的计算过程与R2SDF结构相同, 如图6所示.

图6 R22SDF结构(N=256)Fig.6 Structure of R22SDF (N=256)

在图6的BF2Ⅰ单元中,t为控制输出与-j相乘的时钟, 可实现实部与虚部位置互换. 不同流水线结构所需硬件资源及控制复杂性的比较列于表1. 由表1可见, R22SDF流水线结构在乘法器和存储器所需数量均最少, 因此本文采用R22SDF结构.

表1 不同流水线结构所需硬件资源及控制复杂性的比较

3.2 可变点FFT处理器的硬件架构设计

采用基-4/2混合基算法和流水线R22SDF结构设计可变点FFT处理器的硬件架构, 如图7所示. 由图7可见, 可通过增减蝶形单元实现不同点数的FFT, 从而实现OFDMA系统的核心功能. 各级运算模块结构类似, 均包括控制单元、 蝶形运算数据存储单元、 旋转因子存储单元、 复数乘法运算单元和蝶形运算单元五部分. 其中蝶形运算单元为核心部分, 该单元完成BF2,BF2Ⅰ和BF2Ⅱ的复数加法运算, 其运算单元结构如图8所示.

3.3 功能仿真验证

采用Matlab软件产生一个64=43点的序列, 作为仿真软件Modelsim和FFT处理器的输入, Modelsim仿真结果如图9(A)所示, 通过Quartus中的Signaltap逻辑分析仪采样得到FFT处理器运行结果, 如图9(B)所示. 由图9可见, (A)和(B)的结果一致, 表明设计的FFT处理器各功能模块及整个系统满足设计要求, 功能与时序正确.

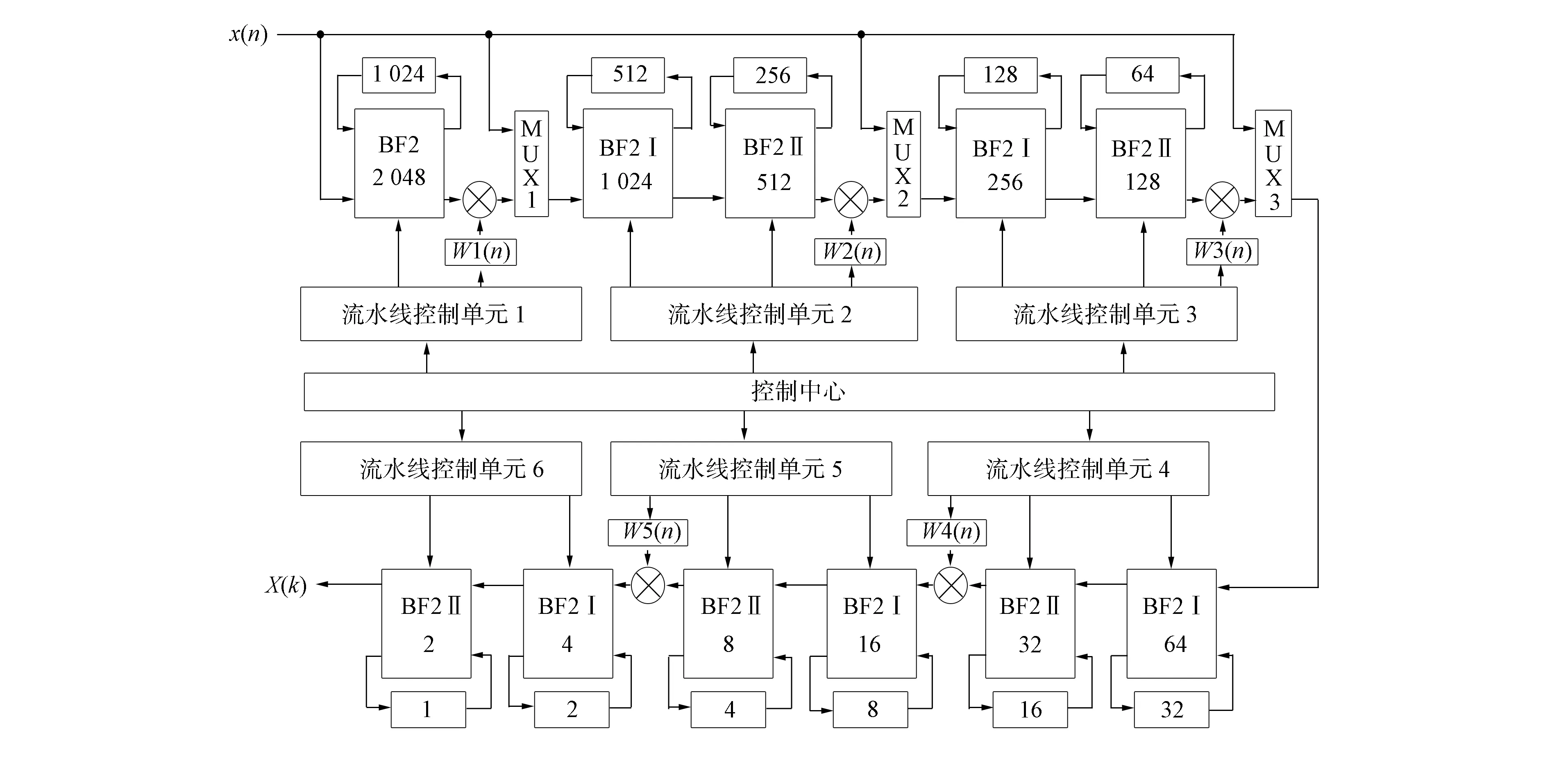
图7 可变点FFT处理器的硬件架构Fig.7 Hardware architecture of variable points FFT processor

图8 BF2Ⅰ(A)和BF2/BF2Ⅱ(B)的运算单元结构Fig.8 Operation unit structure of BF2Ⅰ (A) and BF2/BF2Ⅱ (B)

图9 Modelsim仿真结果(A)与FFT处理器运行结果(B)Fig.9 Simulation results of modelsim (A) and operation results of FFT processor (B)

3.4 信号仿真验证

利用Matlab软件对正弦波和锯齿波进行采样, 得到输入序列, 将FFT处理器运算结果通过Matlab做ifft和生成频谱, 并与Matlab中fft( )函数产生的频谱进行比较.

3.4.1 正弦波信号仿真 利用Matlab函数产生一组1 024=45点正弦波序列点, 信号的采样频率为500 Hz, 为显示方便, 幅值放大104倍.

x(t)=sin(2π×10×t).

(10)

通过Matlab中fft( )函数产生的频谱和FFT处理器运行结果如图10所示. 由图10可见, FFT处理器输出的结果通过函数ifft( )得到的时域信号与输入正弦波信号相同, 输出的频谱与Matlab所得频谱一致, 时域误差与频域误差极小.

(A) 正弦信号时域信号(N=1 024); (B) 利用IFFT得到的时域信号; (C) 时域信号误差;(D) Matlab FFT运算结果; (E) 本文FFT运算结果; (F) 频域信号误差.图10 1 024点正弦波运算结果Fig.10 Operation results for 1 024 points sine wave

3.4.2 锯齿波信号仿真与验证 利用Matlab软件产生一组2 048=2×45点锯齿波序列点, 作为输入信号, 信号的采样频率为50 Hz, 为显示方便, 幅值放大104倍, 通过Matlab中fft( )函数产生的频谱和FFT处理器运行结果如图11所示. 由图11可见, FFT处理器输出的结果通过函数ifft( )得到的时域信号与输入三角波信号相同, 输出的频谱数据与Matlab所得频谱一致, 时域误差与频域误差较小.

(A) 锯齿波信号时域信号(N=2 048); (B) 通过IFFT得到的时域信号; (C) 时域信号误差;(D) Matlab FFT运算结果; (E) 本文FFT运算结果; (F) 频域信号误差.图11 2 048点锯齿波信号运算结果Fig.11 Operation results for 2 048 points sawtooth wave

综上, 本文设计了一种基于FPGA的可变点FFT处理器, 采用DIF基-4/2混合基算法, 通过优化使得基-4算法流图中具有基-2蝶形结构, 有效减少了蝶形迭代的次数, 降低了运算的复杂度, 采用流水线R22SDF结构, 可减少所需存储器和乘法器的数量, 提高各级间的运算速度, 每级蝶形运算可在部分数据完成计算和存储后即开始新一级运算, 实现多级运算交叉进行, 进一步提高了FFT运算速度, 降低控制难度. 最后通过实验对FFT处理器进行功能和信号的仿真验证, 实验结果表明, FFT处理器的有效性和执行效率均满足OFDMA系统应用的需求.

[1] CHEN Jiyang, LEI Yuanwu, PENG Yuanxi, et al. Configurable Floating-Point FFT Accelerator on FPGA Based Multiple-Rotation CORDIC [J]. Chinese Journal of Electronics, 2016, 25(6): 1063-1070.

[2] 刘宝军, 王中训, 钟强, 等. 基于FPGA的FFT算法设计与实现 [J]. 光电技术应用, 2016, 31(3): 46-49. (LIU Baojun, WANG Zhongxun, ZHONG Qiang, et al. Design and Implementation of FFT Algorithm Based on FPGA [J]. Electro-Optic Technology Application, 2016, 31(3): 46-49.)

[3] Prabhu E, Mangalam H, Karthick S. Design of Area and Power Efficient Radix-4 DIT FFT Butterfly Unit Using Floating Point Fused Arithmetic [J]. Journal of Central South University, 2016, 23(7): 1669-1681.

[4] 樊恩辰, 姚馨, 何书专, 等. 基于SystemC的可配置FFT周期精确模型 [J]. 微电子学与计算机, 2014, 31(11): 83-87. (FAN Enchen, YAO Xin, HE Shuzhuan, et al. Cycle-Accurate Configurable FFT Modeling with System C [J]. Microelectronics & Computer, 2014, 31(11): 83-87.)

[5] Huang S J, Chen S G. A High-Throughput Radix-16 FFT Processor with Parallel and Normal Input/Output Ordering for IEEE 802.15.3c Systems [J]. IEEE Transactions on Circuits & Systems Ⅰ: Regular Papers, 2012, 59(8): 1752-1765.

[6] Joshi S P, Paily R. Distributed Arithmetic Based Split-Radix FFT [J]. Journal of Signal Processing Systems, 2014, 75(1): 85-92.

[7] Kim E J, Lee J H, Sunwoo M H. Novel Shared Multiplier Scheduling Scheme for Area-Efficient FFT/IFFT Processors [J]. IEEE Transactions on Very Large Scale Integration Systems, 2015, 23(9): 1689-1699.

[8] 王英喆, 杜蓉. 基于FPGA流水线结构并行FFT的设计与实现 [J]. 电子设计工程, 2015, 23(4): 47-50. (WANG Yingzhe, DU Rong. A Pipelining Architecture Design of Parallel FFT Based on FPGA [J]. Electronic Design Engineering, 2015, 23(4): 47-50.)

[9] Harikrishna K, Rama R T, Labay V A. FPGA Implementation of FFT Algorithm for IEEE 802.16e (Mobile WiMAX) [J]. International Journal of Computer Theory and Engineering, 2011, 3(2): 197-203.

[10] Yang K J, Tsai S H, Chuang G C H. MDC FFT/IFFT Processor with Variable Length for MIMO-OFDM Systems [J]. IEEE Transactions on Very Large Scale Integration Systems, 2013, 21(4): 720-731.

[11] 许朋, 周立青, 刘宇航, 等. 基于FPGA的高性能浮点型FFT处理器设计 [J]. 武汉大学学报(工学版), 2015, 48(1): 120-124. (XU Peng, ZHOU Liqing, LIU Yuhang, et al. Design of a High-Performance Floating-Point Fast Fourier Transform Processor Based on FPGA [J]. Engineering Journal of Wuhan University, 2015, 48(1): 120-124.)

[12] 苏斌, 刘畅, 潘志刚. 基于FPGA的高速浮点FFT/IFFT处理器设计与实现 [J]. 中国科学院大学学报, 2015, 32(2): 259-263. (SU Bin, LIU Chang, PAN Zhigang. Design and Implementation of High-Speed Floating Points FFT Processor Based on FPGA [J]. Journal of University of Chinese Academy of Sciences, 2015, 32(2): 259-263.)

[13] 周景龙. 基于高速FFT结构的频域抗干扰算法的FPGA实现 [J]. 微电子学与计算机, 2014, 31(5): 32-35. (ZHOU Jinglong. An FPGA Implementation of Frequency-Domain Anti-jamming Algorithm Based on a Structure of High-Speed FFT [J]. Microelectronics & Computer, 2014, 31(5): 32-35.)

[14] Lakshmi D V V, Satya N C, Anil K R. Butterfly Design for RADIX-4K DIF FFT [J]. International Journal of Research in Computer and Communication Technology, 2014, 3(10): 1348-1353.

[15] WANG Zeke, LIU Xue, HE Bingsheng, et al. A Combined SDC-SDF Architecture for Normal I/O Pipelined Radix-2 FFT [J]. IEEE Transactions on Very Large Scale Integration Systems, 2015, 23(5): 973-977.

[16] 王天. 基于混合基算法的快速傅立叶变换和反变换在VDSL2中的应用与实现 [D]. 西安： 西安电子科技大学, 2009. (WANG Tian. Application and Implementation of FFT/IFFT Based on Mixed Radix in VDSL2 System [D]. Xi’an: Xidian University, 2009.)