超TD族的自相容源及其守恒律

方 芳, 胡贝贝

(滁州学院 数学与金融学院, 安徽 滁州 239000)

0 引 言

孤立子理论在流体力学、 经典场论、 量子场论、 超导物理和离子物理等领域应用广泛.目前, 孤立子理论的研究已从Hamilton结构、 自相容源、 可积耦合、 守恒律等不同角度得到许多结果. 在可积系统的研究中, 屠规彰[1]给出了一个可有效建立Hamilton结构的方法; 胡星标[2]在无证明的情形下首次提出了超迹恒等式, 是构造超可积方程的超Hamilton系统的有效工具; 马文秀[3]给出了文献[2]的证明, 并应用超迹恒等式构造了超可积方程的超Hamilton结构. 之后, 许多经典的可积系统被推广为超完全可积系统[4-8].

含自相容源的孤立子方程是在寻找新的可积系统过程中发展起来的. 一般地, 源导致孤立波以变速行进, 使得孤子的运动特征发生较大变化. 带自相容源的孤立子方程反映了不同孤波的相互作用. 例如, 含自相容源的KP方程描述了在X-Y平面上传播的长短波之间的相互作用, 含自相容源的KdV方程可描述等离子体重高频波包与一个低频波包的相互作用. 因此, 含自相容源可积方程的研究得到广泛关注[9-11]. 文献[12-19]通过对一些经典的可积系统进行超化, 构造了带自相容源的超可积系统及其超Hamilton结构, 并研究了其守恒律.

目前, 关于TD孤子方程族的研究已有许多结果. 斯仁道尔吉等[20]给出了TD族的换位表示, 并讨论了换位表示与定态TD方程之间的关系; 李雪梅等[21]借助Darboux交换和分解, 得到了广义TD族和一些(2+1)维或(1+1)维非线性演化方程的显式解(包括孤立子解), 特别地, 得到了KP方程的新解; 王四川等[22]用拓展谱问题方法构造了TD族的可积耦合, 并应用二次型恒等式寻求拓展的TD族Hamilton结构. 本文在Loop李超代数的基础上, 构造超TD族及其超Hamilton结构, 以及带自相容源的超TD方程族和无穷守恒律.

1 TD方程族和超TD方程族

[23], 考虑如下TD等谱问题：

(1)

其中:λ为谱参数;u1为位势;φ称为特征函数. 由屠格式[24], 取

(2)

首先解稳定的零曲率方程

V1,x=(U1,V1),

(3)

将U1,V1代入方程(3), 并比较λ-m(m≥0)的系数, 可得(bj+1+cj+1,aj+1)T的递推关系式

(4)

递推算子L有如下形式:

(5)

考虑

(6)

其中Δn为修正项. 将方程(6)代入零曲率方程

(7)

可得TD系统的Hamilton结构

(8)

Hamilton算子J有如下形式:

(9)

令

可得变换后的Lax对：

(10)

可证问题(1)与问题(10)等价, 于是可得谱问题(10)的方程族为式(4), 其中递推算子L如式(5). 谱问题(10)的Hamilton结构为式(8)， 其中Hamilton算子J如式(9).

基于上述等价谱问题, 本文考虑如下超等谱问题：

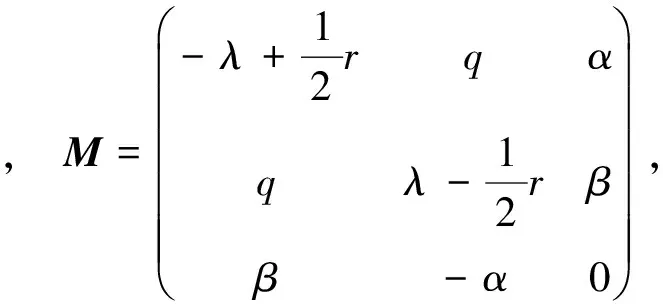
(11)

其中:λ为谱参数;q,r为偶变量;α,β为奇变量. Lie超代数为G=span{e1,…,e5},

(e1,e2)=-2e2, (e1,e3)=2e3, (e2,e3)=-e1, (e5,e1)=(e2,e4)=e5, (e3,e4)=(e2,e5)=0,

(e3,e5)=(e1,e4)=e4, (e4,e4)+=-2e3, (e5,e5)+=2e2, (e4,e5)+=(e5,e4)+=e1,

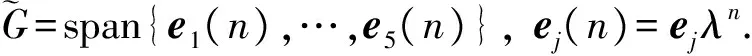
(12)

其中:A,B,C为偶变量;ρ,δ为奇元素. 要得到超TD系统, 首先需解稳定的零曲率方程

Nx=(M,N).

(13)

将M,N代入方程(13), 并比较λ-m(m≥0)的系数, 可得(aj+1,cj+1+bj+1,2δj+1,-2ρj+1)T的递推关系式

(14)

其中递推算子L有如下形式:

这里∂∂-1=∂-1∂=1.

给定一个初始值, 并取所有的积分常数为零, 则所有的aj,bj,cj,ρj,δj(j≥1)可由递推关系式(14)计算得到. 特别地, 取a0=-1, 则前几项结果为

下面考虑谱问题(11)的辅助谱问题, 即时间部分

φtn=Mφ,

(15)

其中

(16)

Δn为修正项,τn=2-1q-1(cn+1+bn+1). 将方程(16)代入零曲率方程

(17)

可得超TD系统

(18)

这里

令n=2, 方程(11)可约化为

(19)

其Lax对为M和N(2),

(20)

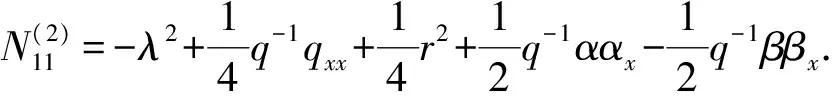
应用超迹恒等式

(21)

并比较λ-n-2的系数可得

(22)

令n=0, 可得γ=0, 故超TD系统(11)有超Hamilton结构

(23)

2 带自相容源的超TD方程族

下面构造带自相容源的超TD系统的可积方程族. 在超TD谱问题

φx=Mφ,φt=Nφ

(24)

中, 令λ=λj, 相应的谱向量φ记为φj, 则可得N个相应线性问题

(25)

其中:Mj=M|λ=λj;Nj=N|λ=λj;j=1,2,…,N. 由于

(26)

其中Φj=(φj1,…,φjN)T,j=1,2,3. 故带自相容源的超TD可积方程族为

(27)

这里:

当n=2时, 可得带自相容源的超TD方程

3 超TD方程族的守恒律

下面构造超TD方程族的守恒律. 首先引入变量

(28)

由谱问题(11), 有

Fx=q+(2λ-r)F+βG-qF2-αFG,

(29)

(30)

设F,G存在, 且将F,G按谱参数λ的负幂展开, 可得

(31)

将式(31)代入方程(29),(30), 并比较λ同次幂的系数, 可得

从而fn和gn的递推公式为

由线性谱问题(24)知,

φ1)t=A+BF+ρG.

所以

(32)

若令

则方程(32)可化为σt=θx. 对于超TD方程(19), 计算易得

(33)

将F,G的展开式(31)与超TD族的方程(19)对应的A,B,ρ代入式(33)可得

令λ的同次幂相等, 可知超TD方程(19)具有无穷多守恒律, 其中σj,θj分别称为守恒密度和连带流. 第一对守恒密度和流为

一般的守恒密度和流为

参考文献

[1] TU Guizhang. The Trace Identity, a Powerful Tool for Constructing the Hamiltonian Structure of Integrable Systems [J]. Journal of Mathematical Physics, 1989, 30(2): 330-338.

[2] HU Xingbiao. An Approach to Generate Superextensions of Integerable Systems [J]. Journal of Physics A: Mathematical and General, 1997, 30(2): 619-632.

[3] MA Wenxiu. Variational Identities and Applications to Hamiltonian Structures of Soliton Equations [J]. Nonlinear Analysis: Theory, Methods & Applications, 2009, 71(12): e1716-e1726.

[4] DONG Huanhe, WANG Xinzeng. Lie Algebras and Lie Super Algebra for the Integrable Couplings of NLS-MKdV Hierarchy [J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(12): 4071-4077.

[5] YU Jing, MA Wenxiu, HAN Jingwei, et al. An Integrable Generalization of the Super AKNS Hierarchy and Its Bi-Hamiltonian Formulation [J]. Commun Nonlinear Sci Numer Simulat, 2017, 43: 151-157.

[6] HAN Jinwei, YU Jing. A Generalized Super AKNS Hierarchy Associated with Lie Superalgebrasl(2|1) and Its Super Bi-Hamiltonian Structure [J]. Commun Nonlinear Sci Numer Simulat, 2017, 44: 258-265.

[7] HU Beibei, XIA Tiecheng, ZHANG Ling. An Integrable Generalization of the Super Kaup-Newell Soliton Hierarchy and Its Bi-Hamiltonian Structure [J/OL]. 2017-06-13. https://arxiv.org/pdf/1706.03929.pdf.

[8] HU Beibei, MA Wenxiu, XIA Tiecheng, et al. Nonlinear Integrable Couplings of a Generalized Super Ablowitz-Kaup-Newell-Segur Hierarchy and Its Super Bi-Hamiltonian Structures [J/OL]. 2017-06-16. https://arxiv.org/pdf/1706.05234.pdf.

[9] HU Xingbiao, WANG Hongyan. Construction of dKP and BKP Equations with Self-consistent Sources [J]. Inverse Problems, 2006, 22(5): 1903-1920.

[10] LI Yishen, ZHANG Lining. Super AKNS Scheme and Its Infinite Conserved Currents [J]. Il Nuovo Cimento A, 1986, 93(2): 175-183.

[11] ZHANG Dajun. TheN-Soliton Solutions of Some Soliton Equations with Self-consistent Sources [J]. Chaos, Solitons and Fractals, 2003, 18(1): 31-43.

[12] LI Li. Conservation Laws and Self-consistent Sources for a Super-CKdV Equation Hierarchy [J]. Physics Letters A, 2011, 375(11): 1402-1406.

[13] WANG Yunhu, CHEN Yong. Conservation Laws and Self-consistent Sources for a Super Integrable Equation Hierarchy [J]. Commun Nonlinear Sci Numer Simulat, 2012, 17(6): 2292-2298.

[14] WANG Hui, XIA Tiecheng. Conservation Laws for a Super G-J Hierarchy with Self-consistent Sources [J]. Commun Nonlinear Sci Numer Simulat, 2012, 17(2): 566-572.

[15] TAO Sixing. Self-consistent Sources and Conservation Laws for Super Coupled Burgers Equation Hierarchy [J]. International Journal of Applied Physics and Mathematics, 2013, 3(4): 252-256.

[16] WANG Hui, XIA Tiecheng. Conservation Laws and Self-consistent Sources for a Super KN Hierarchy [J]. Appl Math Comput, 2013, 219(10): 5458-5464.

[17] 胡贝贝, 张玲, 方芳. Li谱问题的超化及其自相容源 [J]. 吉林大学学报(理学版), 2015, 53(2): 229-234. (HU Beibei, ZHANG Ling, FANG Fang. Super-Li Spectrum Problems and Its Self-consistent Source [J]. Journal of Jilin University (Science Edition), 2015, 53(2): 229-234.)

[18] 胡贝贝, 张玲. 超经典Boussinesq系统的守恒律和自相容源 [J]. 数学杂志, 2016, 36(3): 584-590. (HU Beibei, ZHANG Ling. Conservation Laws and Self-consistent Sources for the Super Classical Boussinesq System [J]. Journal of Mathematics, 2016, 36(3): 584-590.)

[19] HU Beibei, XIA Tiecheng. The Binary Nonlinearization of the Super Integrable System and Its Self-consistent Sources [J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2017, 18(3/4): 285-292.

[20] 斯仁道尔吉, 阿其拉图.TD-族的换位表示 [J]. 内蒙古大学学报(自然科学版), 1994, 25(4): 363-367. (Sirendaoreji, Achilatu. Commutator Representations forTD-Hierarchy [J]. Acta Scientiarum Naturalium Universitatis Neimenggu, 1994, 25(4): 363-367.)

[21] LI Xuemei, NIU Kuihuan. Explicit Solutions for the Generalized TD Hierarchies and Some Nonlinear Evolution Equations [J]. Journal of Zhengzhou University (Natural Science Edition), 2007, 39(3): 1-6.

[22] 王四川, 夏铁成. TD孤子方程族的可积耦合及其哈密顿结构 [J]. 应用数学与计算数学学报, 2013, 27(4): 450-458. (WANG Sichuan, XIA Tiecheng. Integrable Couplings of TD Soliton Equation Hierarchy and Its Hamiltonian Structure [J]. Communication on Applied Mathematics and Computation, 2013, 27(4): 450-458.)

[23] 张玉峰, 张鸿庆. Lax对变换与约束流的Lax表示 [J]. 吉林大学学报(理学版), 2002, 40(2): 114-118. (ZHANG Yufeng, ZHANG Hongqing. Transformation of Lax Pair and Lax Representation of Constrained Flows [J]. Journal of Jilin University (Science Edition), 2002, 40(2): 114-118.)

[24] TU Guizhang, MENG Dazhi. The Trace Identity, a Powerful Tool for Construction the Hamiltonian Structure of Integrable Sysytem (Ⅱ) [J]. Acta Mathematicae Applicatae Sinica, 1989, 5(1): 89-96.