广义耦合非线性薛定谔方程中的达布变换和多孤子解*1

林 机, 郭帮兴

(浙江师范大学 非线性物理研究所,浙江 金华 321004)

广义耦合非线性薛定谔方程中的达布变换和多孤子解*1

林 机, 郭帮兴

(浙江师范大学 非线性物理研究所,浙江 金华 321004)

给出了广义耦合非线性薛定谔方程(GCNLS)的2种达布变换和多孤子解.对于自聚焦型GCNLS，给出了N个亮-亮孤子解，对于散焦型的GCNLS，由第2种达布变换给出了N-暗-暗孤子解.作为例子，文中给出了二孤子相互作用.

广义耦合非线性薛定谔方程;达布变换;多孤子解;孤子相互作用；高孤子

0 引 言

广义耦合非线性薛定谔方程(简称GCNLS)为

式(1)中：a和c是常数;b是一个复常数;符号“*”表示复共轭.在非线性光学中，a和c表示自相位调制效应和交叉相位调制效应，b和b*两项表示四波混频效应.GCNLS(1)具有Lax对、双线性形式和根据黎曼-希尔伯特方法得到的N个孤子解[1-2].近来，利用τ函数方法给出了广义耦合非线性方程(1)的N-暗-暗孤子解[3].众所周知，一个非线性偏微分方程若具有可解的逆散射变换、N-孤子解、双线性形式、Lax对和达布变换(DT)等特性，就称该方程是完全可积.对于标准的耦合非线性薛定谔方程(简称CNLS)，亦称为Manakov方程，且自聚焦型的CNLS，利用逆散射方法和达布变换及双线性方法得到了N-亮-亮孤子和N-亮-暗孤子解[4-7].近来，利用达布变换和双线性方法，研究了非线性自散焦式和聚焦散焦混合型的CNLS的孤子解[8-10]，对于自散焦的CNLS，利用双线性方法可以得到N-亮-暗孤子和2-暗-暗孤子解[11-12].通过逆散射变换，一些简单的暗-暗孤子和亮-暗孤子可以被构造出来[13].文献[9-10]给出了自聚焦-散焦混合型的CNLS的2-和3-亮-亮孤子和亮-暗孤子解.尽管求解自散焦型的CNLS的方法有很多，但是多暗孤子还未能给出.因此，如何获得自散焦型CNLS的多暗孤子是非常重要的研究课题.最近，Ohta和Yang通过τ函数方法构造了自散焦型的CNLS与GCNLS的一般N-暗-暗孤子解.求具有Lax对的非线性偏微分系统的多孤子解，达布变换方法是非常有效的[14-19]，所以我们相信可以通过达布变换得到GCNLS的多孤子解.

本文中，笔者主要研究了GCNLS(1)的达布变换和多孤子解.第2节将构造自聚焦和自散焦型的GCNLS方程(1)的达布变换，推导给出GCNLS方程在自聚焦型情况下的多-亮-亮孤子和自散焦情况下的多-暗-暗孤子.最后是结果和讨论.

1 达布变换

GCNLS(1)具有如下的Lax对:

式(2)中：Φ(x,t)是矩阵函数;λ为谱参量;以及

其中:r1=-ap*-bq*,r2=-b*p*-cq*.通过直接计算表明，满足式(2)相容条件可以得到GCNLS(1).显然，GCNLS(1)的达布变换应该有以下形式：

这里的G是一个非奇异矩阵，并且满足

GCNLS(1)的Lax对在达布变换(2)变换下其形式保持不变，即

要求满足以下关系式

如果能给出一个3×3的矩阵M(G)，那么就可以得到GCNLS(1)的达布变换(3)，最后由达布变换(3)得到GCNLS(1)的新解.根据一般计算达布变换原则，式(3)的矩阵元素是Lax对(2)中的解.事实上，引入以下幺正变换:

这里φ满足以下的Lax对:

这里

变量u和v满足CNLS方程.通过以上的变换关系可以得到自聚焦型的GCLNS(1)的达布变换.

以下笔者将研究相应的达布变换和自聚焦型和自散焦型的GCNLS(1)的多孤子解.

1.1自聚焦型GCNLS中的达布变换和多孤子解

对于自聚焦型的GCNLS(1)，其参量a>0,c>0,设Lax对(2)中的谱参量分别为λ1=μ，λ2=λ3=μ*及解为Φ(j)(j=1,2,3)，即

Φ(j)=(iμ*J+U)Φ(j),j=2,3.

(10)

若能够得到方程(9)的解Φ(1)，通过寻找Φ(2,3)和Φ(1)的关系，进而给出方程(10)的解.笔者发现

从式(11)得到φ(1)和φ(j)满足如下关系:

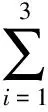
式(12)中：φ(1)和φ(j)是式(8)的谱参量(λ1,λj)=(μ1,μ*1)的解.最后，笔者给出式(3)中的矩阵G

及矩阵M

M=GΛG-1=ΩHΛH-1Ω-1. (14)

因此，由式(14)可以做一次达布变换，从方程(1)的一种子解(p0,q0)出发就能得到方程(1)的一个新解

若做N次达布变换，就能得到GCNLS方程(1)的一般迭代新解

这里

(18)

式(18)中，φ(j)是式(8)关于λ=μj和Φ(1)i=φ(1)i(i=1,2,3)的解.

1.2自散焦GCNLS的达布变换和一般迭代解

通过上述传统的达布变换方法,很难获得自散焦型的GCNLS(1)的一般迭代解.受文献[16]中的方法启发，尝试使用简单的达布变换方法寻找GCNLS的多暗孤子解.对于自散焦型的GCNLS(1)中的参量，要求a<0,c<0.式(8)中的第1个式子中伴随的谱问题可以写成下面形式

利用规范变换构建式(8)的达布变换.假设在λ=μ1时有式(8)谱问题的一个解Φ1，以及在λ=v1时有式(19)伴随谱问题的一个解Ψ1.然后式(8)的达布变换

和伴随谱问题式(19)的达布变换

因此，就可以给出Q的迭代关系式

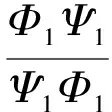
同时我们假设Q矩阵函数具有如下对称性:

Q的对称性意味着：如果Φ1是λ=λ1(λ∈R)谱问题(8)的特殊矢量解，那么Φ+1M就是λ=λ1的伴随谱问题(19 )的特殊解.

为了满足对称性(23)，笔者选择

和

其中φ1和ψ1是复函数.可以很容易证明式(24)和式(25)特殊的选择可以使式(22)满足对称性

Q[1]†=-MQ[1]M-1.

因此，单-暗-暗孤子解为

式(26)中,

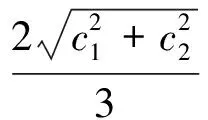
以及对于所有的(x,t)∈R2，Im(φ1,ψ1)≠0.假设我们选择不同的2N个μ1,μ2,…,μN;v1,v2,…,vN实数，并能找到相应的矢量函数Φ和Φ+M,则通过反复迭代达布变换(20)和(21)，就能给出N次的达布变换.若

Φi=Φ(λ=μi)，Ψi=Φ†(λ=μi)M，

则得到了方程(1)的N次迭代解

(28)

其中，

2 GCNLS的多孤子解

一般来说，通过选取不同种子解，可以得到GCNLS方程(1)的不同类型的孤子解.这里，笔者给出2种类型的孤子解.

2.1自聚焦型GCNLS的多亮-亮孤子

取GCNLS(1)的种子解p=q=1,N=1，把它们代入式(8)，从中可解得φ(1)k(k=1,2,3):

并且从迭代公式(16)得到GCNLS(1)的1-亮-亮孤子解

式(30)中：ε1=2μ12(-x+4μ11t);μ1=μ11+iμ12.若取N=2，就能得到GCLNS 的2-亮-亮孤子解

式(31)中：

式(32)中：Ak(k=1,2,3,4,5,6)为任意常数.令μ1=-0.2+i，μ2=0.2+i，a=3,b=1+i，A1=A2=A3=A4=-A5=A6=c=1，将这些参数代入式(32)和式(31)，就能导出p和q的2个孤子解.图1分别显示了GCNLS(1)中二场振幅为2个亮孤子传播特征，表明2个孤子碰撞前后，它们传播的方向、速度及形状都未发生变化.

图1 |p|2和|q|2的2-亮-亮孤子传播

2.2自散焦型GCNLS的多-暗-暗孤子解

选择Lax对(8)的u=c1exp[-2i(c21+c22)t]，v=c2exp[-2i(c21+c22)t],c1,c2∈R为GCNLS(1)的种子解，容易验证下式满足式(24)和式(25)的Lax对(8)和(19)的一个解

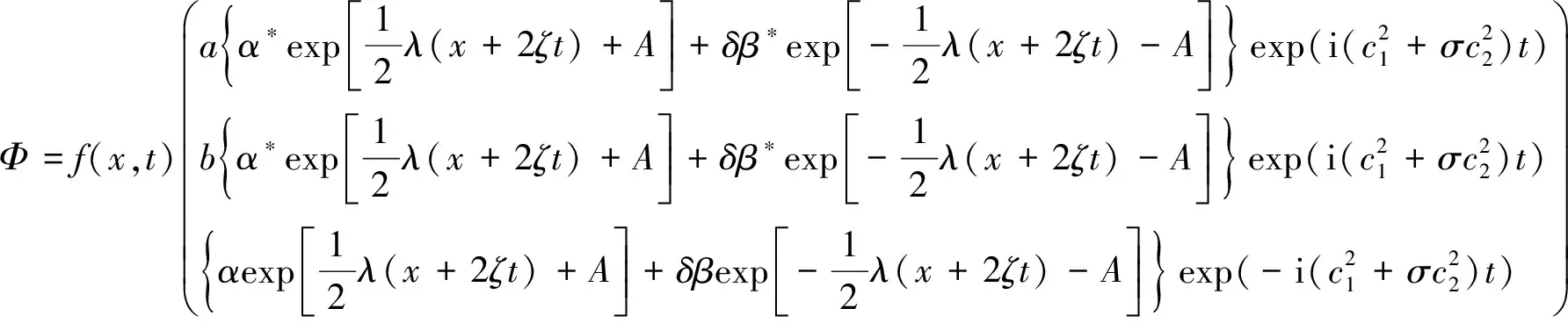
Ψ=Φ†1M|μ=v.

图2 |p|2和|q|2的单暗-暗孤子传播

取式(27)中N=2，可以得到2-暗-暗孤子

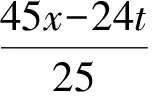
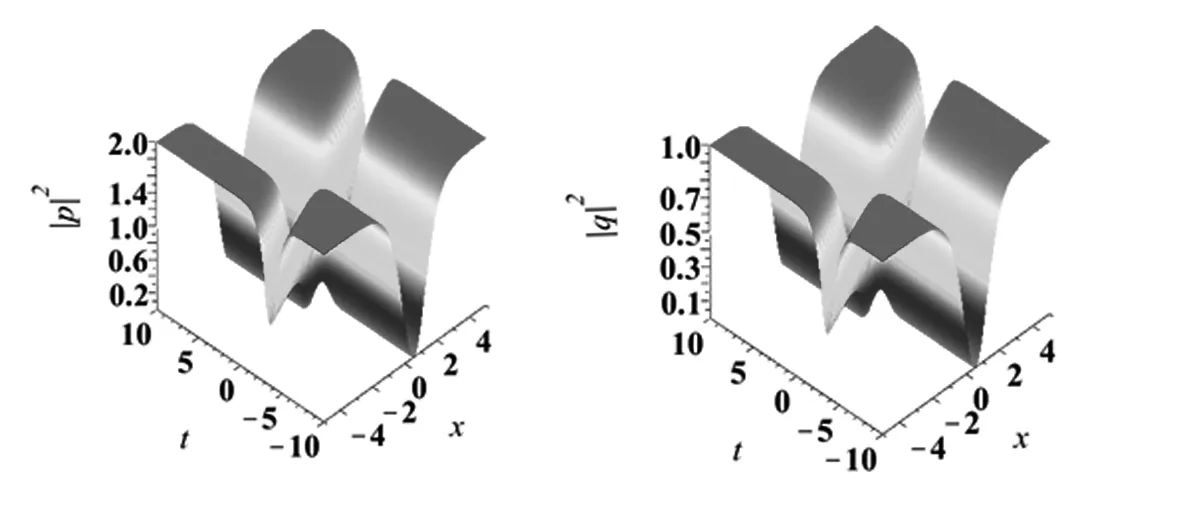
图3 |p|2和|q|2的2-暗-暗孤子传播

3 结果与讨论

笔者分别得到了自聚焦型和自散焦型的GCNLS(1)达布变换和多孤子解.通过构造GCNLS的达布变换，分别得到自聚焦型GCNLS的N-亮-亮孤子和自散焦型GCNLS的N-暗-暗孤子.以2个孤子(包括聚焦非线性GCNLS的2个亮-亮孤子和散焦非线性GCNLS的2个暗-暗孤子)的传播为例，讨论2个孤子相互作用性质，发现在传播过程中它们的振幅和传播速度都没有发生变化.事实上，对于自聚焦和自散焦混合型(a>0,c<0)的GCNLS,通过简单的达布变换，可以很容易地获得方程的N-亮-暗孤子解.

致谢:感谢楼森岳教授和凌黎明博士的有益讨论.

[1]Wang Dengshan.Symmetries and prolongation structure theory of some nonlinear wave equation[D].Beijiang:Chinese Academy of Sciences,2008.

[2]Wang Dengshan,Zhang Dajun,Yang Jianke.Integrable properties of the general coupled nonlinear Schrödinger equations[J].J Math Phys,2010,51(2):023510.

[3]Ohta Y,Wang Dengshan,Yang Jianke.GeneralN-Dark-Dark solitons in the coupled nonlinear Schrödinger equations[J].Stud Appl Math,2011,127(5):345.

[4]Matveev V B,Salle M A.Differential-difference evolution equation II:Darboux transformation for the Toda lattice[J].Lett Math Phys,1979,3(3):425-429.

[5]Manakov S V.Nonlinear Fraunhofer diffraction[J].Zh Eksp Teor Fiz Sov Phys JETP,1974,38(4):693-696.

[6]Park Q H,Shin H J.Systematic construction of vector solitons[J].IEEE J SEL TOP QUANT,2002,8(8):432-439.

[7]Radhakrishnan R,lakshmanan M,Hietarinta J.Inelastic collision and switching of coupled bright solitons in optical fibers[J].Phys Rev E,1997,56(4):2213.

[8]Park Q P,Shin H J.Systematic construction of vector solitons[J].IEEE J of Selected Topics in Quantun Electronics,2002,8(3):432.

[9]Kanna T,Lakshmanan M,Tchofo P,et al.Soliton collisions with shape change by intensity redistribution in mixed coupled nonlinear Schrödinger equations[J].Phys Rev E,2006,73(2):026604.

[10]Vijayajayanthi M,Kanna T,Lakshmanan M.Bright-dark solitons and their collisions in mixed N-coupled nonlinear Schrödinger equations[J].Phys Rev A,2008,77(1):013820.

[11]Sheppard A P,Kivshar Y S.Polarized dark solitons in isotropic Kerr media[J].Phys Rev E,1997,55(10):4773.

[12]Radhakrishnan R,Lakshmanan M.Bright and dark soliton solutions to coupled nonlinear Schrödinger equations[J].J Phys A:Math Gen,1995,28(10):2683.

[13]Prinari B,Ablowitz M J,Biondini G.Inverse scattering transform for the vector nonlinear Schrödinger equation with nonvanishing boundary conditions[J].J Math Phys,2006,47(6):063508.

[14]Li Yishen.The reductions of the Darboux transformation and some solutions of the soliton equations[J].J Phys A:Math Gen,1996,29(9):4187.

[15]Lin Ji,Ren Bo,Li Huamei,et al.Soliton solutions for two nonlinear partial differential equations using a Darboux transformation of the Lax pairs[J].Phys Rev E,2008,77(3):036605.

[16]Mänas M.Darboux transformations for the nonlinear Schrödinger equations[J].J Phys A:Math Gen,1996,29(17):7721.

[17]Lmai K.Generalization of the Kaup-Newell Inverse scattering formulation and darboux transformation[J].J Phys Soc Jap,1999,68(2):355.

[18]Steudel H.The hierarchy of multi-soliton solutions of the derivative nonlinear Schrödinger equation[J].J Phys A:Math Gen,2003,36(7):1931.

[19]Ling Liming,Liu Qingping.Darboux transformation for a two-component derivative nonlinear Schrödinger equation[J].J Phys A:Math Theor,2010,43(11):434023.

(责任编辑 杜利民)

DarbouxtransformationsandMulti-solitonssolutionsforthegeneralcouplednonlinearSchrodingerequation

LIN Ji, GUO Bangxing

(InstituteofNonlinearPhysics,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

Multi-solitons solutions of general coupled nonlinear Schrödinger equation(GCNLS) were obtained by two Darboux transformations(DT).N-bright-bright solitons for the focusing type of GCNLS were derived by the traditional DT method andN-dark-dark solitons for the defocusing type were presented by the simpler-looking DT. The interactions of multi-solitons were also discussed.

general coupled nonlinear Schrödinger equation; Darboux transformations; Multi-solitons solutions； interaction solitons; bright soliton

10.16218/j.issn.1001-5051.2015.02.001

2015-01-06

国家自然科学基金资助项目(11175158)

林 机(1965-)，女，浙江永康人，教授，博士.研究方向：非线性物理.

O411

A

1001-5051(2015)02-0121-08