Clifford分析中广义超正则函数向量的非线性边值问题

杨静梅, 李尊凤,2, 杨贺菊

(1. 河北科技大学 理学院, 石家庄 050018; 2. 河北师范大学 数学与信息科学学院, 石家庄 050024)

Clifford分析[1]主要研究定义在欧氏空间取值于不可交换的Clifford代数的函数的性质. 与单元复分析中的解析函数相同, Clifford分析中的正则函数为Dirac方程的基本解, 而Dirac算子是欧氏度量下Laplace算子的分解因子. 相对于复分析中的解析函数, Clifford分析中的正则函数也有较好的性质, 如Cauchy型积分公式、 Cauchy型定理、 Taylor展开式等. 但自变量x的幂在Clifford分析中不是正则函数.

Clifford分析中的超正则函数[2]是修正Dirac算子M解空间中的元素, 而M为双曲度量下广义Laplace算子的分解因子, 所以超正则函数是另一种流形结构上的全纯函数. 该类函数也有较好的性质, 如Cauchy型积分公式、 Cauchy型定理及高阶导数估值定理等[3-5]. 文献[6-7]研究了超正则函数的分解定理、 表示定理和Plemelj公式, 完善了超正则函数理论； 文献[8]研究了双曲空间中Laplace-Beltrami方程的一个带位移的非边值问题; 文献[9]研究了Clifford分析中一个广义超正则函数的非线性边值问题. 本文在上述结果的基础上考虑一类广义超正则函数向量的积分表达式, 并利用Schauder不动点定理研究一类广义超正则函数向量的非线性边值问题.

1 预备知识

设e1,e2,…,en是n的标准正交基, An()是以e0=1,e1,e2,…,en,e1e2,e1e3,…,e1en,e2e3,e2e4,…,e2en,…,e1e2,…,en为基的实Clifford代数. Clifford代数中可结合不可交换的乘法运算满足下列规则:

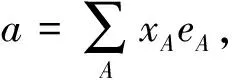
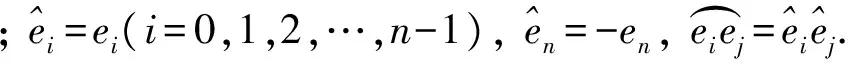
设Ω⊂n+1是一个连通开集, 定义在Ω上取值于Clifford代数An()的函数f(x)可表示为其中fA(x) 为实值函数. 若对任意的A, 有fA(x)∈Cr(Ω), 则称f(x)∈Cr(Ω), 若fA(x)∈H(Ω,β), 则称f(x)∈H(Ω,β).

定义1[1]设Ω⊂n+1是一个连通开集, 若对任意的x=(x0,x1,…,xn)∈Ω, 函数f:Ω→An()满足Df(x)则称f(x)为Ω上的正则函数.

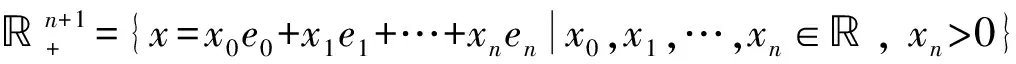
设F(x)=(f1(x),f2(x),…,fk(x)),H(x)=(h1(x),h2(x),…,hk(x))是Ω上的函数向量, 定义加法运算和乘法运算如下:

F(x)±H(x)=(f1(x)±h1(x),…,fk(x)±hk(x)),

F(x)⊗H(x)=(f1(x)h1(x),…,fk(x)hk(x)).

|F+H|>≤|F|>+|H|>, |F⊗H|>≤J1|F|>|H|>.

若对任意的x,x′∈Ω, 有

‖F+H‖β≤‖F‖β+‖H‖β, ‖F⊗H‖β≤J3‖F‖β‖H‖β.

定义4[7]若fi(x)(i=1,2,…,k)为其定义域上的正则(超正则)函数, 则称F(x)=(f1(x),f2(x),…,fk(x))为其定义域上的正则(超正则)函数向量.

定义5设Ω如定义2所述, 若对任意的x∈Ω,fi(x)(i=1,2,…,k)均为广义超正则函数, 则称F(x)=(f1(x),f2(x),…,fk(x))为Ω上的广义超正则函数向量, 即

2 广义超正则函数向量的积分表达式

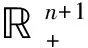
有以下性质:

1) |TΩg(y)|>≤J4|g|>p,n+1;

3)DTΩg(y)=g(y).

引理2[2]设Ω如引理1所述, 若φ∈H(Ω,β), 则

有如下性质:

2) 当y∈∂Ω时, 该奇异积分在Cauchy主值意义下收敛, 记为Φ(y)=S∂Ωφ(y).

其中:

ωn+1为n+1中单位球的表面积.

证明： 设Ψ(y)=f(y)-TΩω(y), 则

又因为

所以

于是f(y)=TΩ(ω(y))+Ψ(y), 其中Ψ(y)为任一超正则函数.

定理2在定理1的条件下, 对任意的y0∈∂Ω, 有

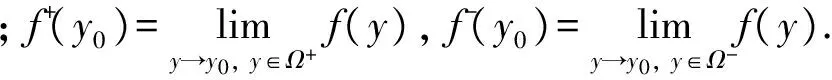
证明: 在定理1的结论中取Ψ(y)为引理2中的Φ(y), 则有

f+(y0)=Φ+(y0)+TΩω(y0),f-(y0)=Φ-(y0)+TΩω(y0).

由超正则函数的Plemelj公式[3]可得

其中:ωi2(x)=Qωi(x);ωi(x)∈Lp,n+1(Ω). 则F(y)有如下积分表达式:

F(y)=(TΩω1(y)+Ψ1(y),TΩω2(y)+Ψ2(y),…,TΩωk(y)+Ψk(y)),

证明: 由定理1可知,fi(y)=TΩωi(y)+Ψi(y)(i=1,2,…,k), 将其代入F(y)可得结论.

定理4在定理3的条件下, 对任意的y0∈∂Ω, 有:

(1)

其中:ωi(y)(i=1,2,…,k)为定理3中的函数;S∂Ωφi(y0)(i=1,2,…,k)为引理2中的奇异积分算子, 即

式中φi(x)∈H(∂Ω,β).

证明: 在定理3的结论中, 取Ψi(y)=Φi(y)(i=1,2,…,k), 则由定理2可得

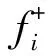
所以有式(1).

3 广义超正则函数向量的非线性边值问题

A(t)⊗F+(t)+B(t)⊗F-(t)=N(t)M(t,F+(t),F-(t)),

A(t)=(a1(t),a2(t),…,ak(t)),B(t)=(b1(t),b2(t),…,bk(t)),

N(t)=(n1(t),n2(t),…,nk(t)),

M(t,F+(t),F-(t))=(m1(t,F+(t),F-(t)),m2(t,F+(t),F-(t)),…,mk(t,F+(t),F-(t))),

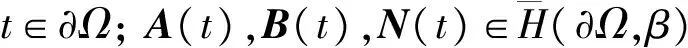
引理3[3]设Ω如上所述,φ∈H(∂Ω,β), 且θφ=S∂Ωφ-φ/2. 则有

‖θφ‖β≤J5‖φ‖β, ‖S∂Ωφ‖β≤J5‖φ‖β, ‖S∂Ωφ+φ/2‖β≤J5‖φ‖β,

其中J5为与φ无关的正常数.

‖θφ‖β≤J6‖φ‖β, ‖S∂Ωφ‖β≤J6‖φ‖β, ‖S∂Ωφ+φ/2‖β≤J6‖φ‖β,

其中J6为与φ无关的正常数.

证明: 由函数向量的定义及引理3可得结论.

F(y)=TΩω(y)+Φ(y);S∂Ωφ=(S∂Ωφ1,S∂Ωφ2,…,S∂Ωφk);TΩω=(TΩω1,TΩω2,…,TΩωk).

证明: 将定理4代入问题1, 再由定理3可得结论.

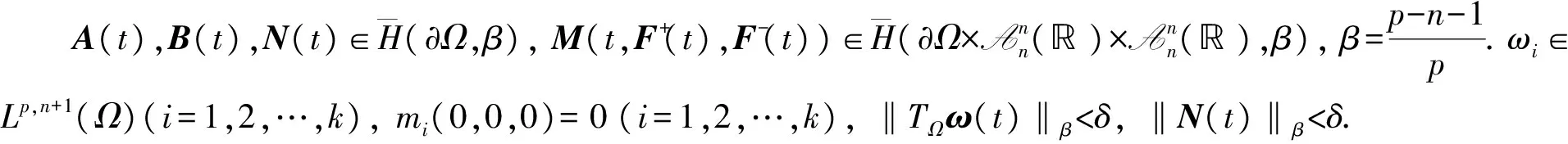
则当

μ=J3J6‖A(t)+B(t)‖β+J3‖1-B(t)‖β<1

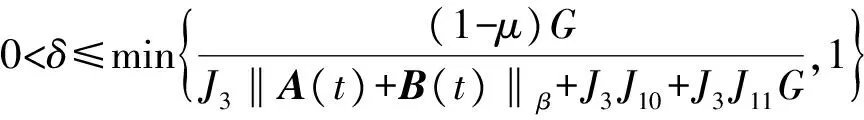
1) 证明R是映射T到自身的映射. 由定理条件及定理5可知,

又因为

所以

‖M(t,F+(t),F-(t))‖β≤J9+J8‖φ‖β+3J7+2J6‖φ‖β=J10+J11‖φ‖β.

于是

2) 证明R为T上的连续映射. 任取φn(t)∈T, 并设φn(t)在∂Ω上一致收敛于φ(t), 则对任意的ε>0, 当n充分大时, 有‖φn(t)-φ(t)‖<ε. 由定理5可知

|S∂Ωφn(t)-S∂Ωφ(t)|>≤J6‖φn-φ‖β,

所以

由μ<1, 有

又因为‖N‖β<δ<1, 所以

因此R为T上的连续映射, 所以R为T到自身的连续映射.

[1] Brackx F, Delanghe R, Sommen F. Clifford Analysis [M]. Boston: Pitman Books Limits, 1982.

[2] Eriksson S L. Integral Formulas for Hypermonogenic Functions [J]. Bull Belg Math Soc, 2004, 11(5): 705-717.

[3] QIAO Yuying. A Boundary Value Problem for Hypermonogenic Functions in Clifford Analysis [J]. Science in China (Ser A), 2005, 48: 324-333.

[4] ZHANG Zhongxiang. Some Properties of Operators in Clifford Analysis [J]. Complex Variables and Elliptic Equations, 2007, 52(6): 455-473.

[5] 张忠祥, 杜金元. 关于Clifford分析中的某些Riemann边值问题与奇异积分方程 [J]. 数学年刊, 2001, 22A(4): 421-426. (ZHANG Zhongxiang, DU Jinyuan. On Certain Riemann Boundary Value Problems and Singular Integral Equations in Clifford Analysis [J]. Chinese Annals of Mathematics, 2001, 22A(4): 421-426.)

[6] QIAO Yuying, Bernstein S, Eriksson S L, et al. Function Theory for Laplace and Dirac-Hodge Operators on Hyperbolic Space [J]. Journal d’Analyse Mathématique, 2006, 98(1): 43-64.

[7] YANG Heju, XIE Yonghong, QIAO Yuying. A Kind of Boundary Value Problem for Hypermonogenic Function Vectors [J]. Journal of Mathematical Research and Exposition, 2011, 31(3): 490-496.

[8] 杨贺菊, 李海萍. 双曲空间中Laplace-Beltrami方程的一个带位移的边值问题 [J]. 数学的实践与认识, 2012, 42(16): 253-257. (YANG Heju, LI Haiping. A Boundary Value Problem with a Shift for the Laplace-Beltrami Equation in Hyperbolic Space [J]. Mathematics in Practice and Theory, 2012, 42(16): 253-257.)

[9] 杨贺菊, 李海萍. Clifford分析中广义超正则函数的一个非线性边值问题 [J]. 数学的实践与认识, 2014, 44(8): 241-246. (YANG Heju, LI Haiping. A Nonlinear Boundary Value Problem for the Generalized Hypermonogenic Functions in Clifford Analysis [J]. Mathematics in Practice and Theory, 2014, 44(8): 241-246.)