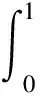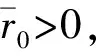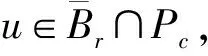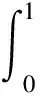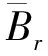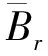一类具有无穷点积分边界条件非线性分数阶微分方程解的存在性与多解性
2018-01-26耿鑫彪
耿鑫彪, 刘 雯
(吉林大学 数学学院, 长春 130012)
0 引 言
分数阶微积分及微分方程在分形、 黏弹性力学、 空气动力学等领域应用广泛[1-2]. 目前, 非线性泛函分析中的方法和技巧是研究分数阶微分方程的有效工具[3-8]. 文献[9]研究了一类带有无穷点积分边界条件的非线性分数阶微分方程(FBVP):
(1)
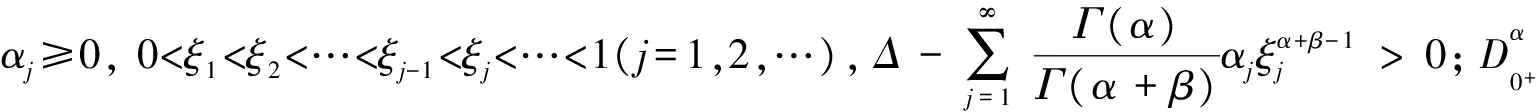
1 引 理
引理1[9]假设y(t)∈C([0,1]), 则边值问题
(2)
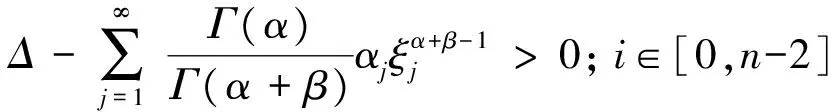

式中
(3)
且
G(t,s)称为边值问题(2)的Green函数. 显然,G(t,s)是一个连续函数.
引理2[9]假设p(0)>0, 则p(s)>0,s∈[0,1]且p(s)是单调不减函数.
引理3[9]函数G(t,s)满足如下条件:


3)G(t,s)>0, ∀t,s∈(0,1).
2 主要结果

Pc⊂E,Pc={u∈E|u(t)≥0,t∈[0,1]}.
∀0 Br={u∈Pc: ‖u‖ 本文假设如下条件成立: (H2)f: [0,1]×[0,∞)→[0,∞)连续,f(t,0)不恒为0. 定义算子A:C[0,1]→C[0,1], (4) 显然, 算子A的不动点即为边值问题(1)的解. 当假设条件(H1),(H2)成立时,A(Pc)⊆Pc. 应用Arzel-Ascoli定理[10-11]可知,A是一个全连续算子. 定义算子T:C[0,1]→C[0,1], (5) 显然,T:Pc→Pc是一个全连续线性算子. 由Krein-Rutmann定理[12], 谱半径r(T)≠0, 且T有一个正特征函数φ1, 对应于第一特征值λ1(λ1=(r(T))-1). 假设: (H7) 存在r0>0, 使得 ∀0 其中τ∈(0,1), 有p(t)不恒为0,t∈[τ,1-τ]. 定理1假设条件(H3),(H4)成立, 则FBVP(1)至少有一个正解. 证明: 由(H3), 存在r>0,ε>0, 使得 f(t,u)≥(λ1+ε)u,t∈[0,1],u∈[0,r]. 不失一般性, 假设A在 ∂Br∩Pc内没有不动点. 令 u-Au≠μφ1, ∀u∈∂Br∩Pc,μ≥0. (6) 否则, 存在u1∈∂Br∩Pc且μ1≥0, 使得u1-Au1=μ1φ1, 因此u1≥μ1φ1. 令τ*=sup{τ|u1≥τφ1}.T是正线性算子, 从而 (λ1+ε)T(u1)≥λ1T(u1)≥τ*λ1T(φ1)=τ*φ1. 因此 u1=Au1+μ1φ1≥(λ1+ε)Tu1+μ1φ1≥(τ*+μ1)φ1, 与τ*的定义矛盾. 故式(6)成立, 且 i(A,Br∩Pc,Pc)=0. (7) 另一方面, 由(H4), 存在ε∈(0,λ1),m>0, 使得 f(t,u)≤(λ1-ε)u+m, ∀u≥R1,t∈[0,1]. 令 W∶={u∈Pc|u=μAu,μ∈[0,1]}, (8) 则 (9) i(A,BR∩Pc,Pc)=1. (10) 由式(7)和式(10), 有 定理2假设(H5),(H6)成立, 则FBVP(1)至少有一个正解. 证明: 证明方法与文献[8]中的定理3.2类似, 故忽略细节. 由假设条件(H5), 有 i(A,Br∩Pc,Pc)=1. (11) 由假设条件(H6), 有 i(A,BR∩Pc,Pc)=0. (12) 定理3假设条件(H3),(H7)成立, 则FBVP(1)至少有一个正解. 证明: 用证明定理1的方法, 由(H1), 有 i(A,Br∩Pc,Pc)=0. (13) 由(H7), 选择r0>r, 有 ∀0 令 u≠μAu, ∀u∈∂Br0∩Pc,μ∈[0,1]. (14) 否则, 存在u1∈∂Br0∩Pc,μ1∈[0,1], 使得u1=μ1Au1. 注意到 因此, ‖u1‖>‖Au1‖≥μ1‖Au1‖, 与u1=μ1Au1矛盾. 从而式(14)成立, 且 i(A,Br0∩Pc,Pc)=1. (15) 因此, 定理4假设条件(H4),(H8)成立, 则FBVP(1)至少有一个正解. 证明: 由(H4), 有 i(T,BR∩Pc,Pc)=1. (16) 其中τ∈(0,1), 使得p(t)不恒为0,t∈[τ,1-τ]. 令 (17) (18) 推论1假设条件(H6),(H7)成立, 则FBVP(1)至少有一个正解. 证明: 若(H6),(H7)成立, 可知 i(A,BR∩Pc,Pc)=0,i(A,Br0∩Pc,Pc)=1. 易得 因此FBVP(1)至少有一个正解. 由推论1可知如下结论成立: 推论2假设条件(H5),(H8)成立, 则FBVP(1)至少有一个正解. 推论3假设条件(H3),(H6),(H7)成立, 则FBVP(1)至少有两个正解. 推论4假设条件(H4),(H5),(H8)成立, 则FBVP(1)至少有两个正解. [1] Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations: North-Holland Mathematics Studies, Vol.204 [M]. Amsterdam: Elsevier, 2006. [2] Sabatier J, Agrawal O P, Tenreiro Machado J A. Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering [M]. Dordrecht: Springer, 2007. [3] LIU Suli, LI Huilai, DAI Qun. Nonlinear Fractional Differential Equations with Nonlocal Integral Boundary Conditions [J/OL]. Advances in Difference Equations, 2015-06-18. doi: 10.1186/s13662-015-0534-3. [4] WANG Wenli, TIAN Jingfeng. Generalized Monotone Iterative Method for Integral Boundary Value Problems with Causal Operators [J]. Journal of Nonlinear Science and Applications, 2015, 8(5): 600-609. [5] LIU Suli, LI Huilai, DAI Qun, et al. Existence and Uniqueness Results for Nonlocal Integral Boundary Value Problems for Fractional Differential Equations [J/OL]. Advances in Difference Equations, 2016-05-03. https://doi.org/10.1186/s13662-016-0847-x. [6] ZHANG Xingqiu. Positive Solutions for a Class of Singular Fractional Differential Equation with Infinite-Point Boundary Value Conditions [J]. Applied Mathematics Letters, 2015, 39: 22-27. [7] CUI Yujun. Uniqueness of Solution for Boundary Value Problems for Fractional Differential Equations [J]. Applied Mathematics Letters, 2016, 51: 48-54. [8] ZHANG Xingqiu, WANG Lin, SUN Qian. Existence of Positive Solutions for a Class of Nonlinear Fractional Differential Equations with Integral Boundary Conditions and a Parameter [J]. Applied Mathematics and Computation, 2014, 226: 708-718. [9] LIU Suli, LIU Junpeng, DAI Qun, et al. Uniqueness Results for Nonlinear Fractional Differential Equations with Infinite-Point Integral Boundary Conditions [J]. J Nonlinear Sci Appl, 2017, 10(3): 1281-1288. [11] Ascoli G. Le Curve Limiti di una VarietData di Curve [J]. Rend Accad Lincei, 1884, 18: 521-586. [12] Krasnosel’skiǐ M A. Positive Solutions of Operator Equations [M]. [S.l.]: Noordhoff Ltd, 1964.