A Novel Distributed Optimal Adaptive Control Algorithm for Nonlinear Multi-Agent Differential Graphical Games

Majid Mazouchi,Mohammad Bagher Naghibi-Sistani,and Seyed Kamal Hosseini Sani

I.INTRODUCTION

RESEARCH on distributed control of multiagent systems linked by communication networks has been well studied in[1]−[7].This grow ing field,is mainly applicable to a variety of engineering systems such as formation of a group of mobile robots[8],distributed containment control[9],vehicles formation control[10],sensor networks[11],[12],networked autonomous team[13],distributed electric power system control[14],[15]and synchronization of dynamical processes.There are many advantages for distributed control such as less computational complexity and no need for a centralized decision-making center.

Distributed control problems can be classified into two main groups,namely leaderless consensus(distributed regulation)and leader-follower concensus(distributed tracking)problems.In the leaderless consensus all agents converge to an uncontrollable common value(consensus value)which depends ontheir initial states in the communication network[16]−[19].On the other hand,the problem of leader-follower consensus[20]−[23],which is the problem of interest in this paper,requires that all agents synchronize to a leader or control agent who generates the desired reference trajectory[20],[24].

Game theory[25],[26]provides a proper solution framework for formulating strategic behaviors,where the strategy of each player depends on the actions of itself and other players.Therefore,it has become the theoretical framework in the field of multi-player games[27]−[30].Differential game is a branch of game theory which addresses dynamical interacting multi agent decision control problems.A new class of differential games is called differential graphical game[31],where the error dynamics and performance index of each player depends on itself and its neighbors in the game communication graph topology.In differential graphical game,the players’goal is to find a set of policies that are admissible,i.e.,control policies that ensure the stability of the overall system,in order to guarantee global synchronization,local optimization and Nash equilibrium achievement.In order to find the Nash equilibrium,one has to solve a set of coupled Hamilton-Jacobi(HJ)equations.These coupled HJ equations are difficult or impossible to solve analytically and they depend on the graph topology interactions.Therefore,in order to approximately solve the coupled HJ equations in an online fashion,numerical methods such as reinforcement learning(RL)methods[32]are required.Approximate dynamic programming(ADP)[33]is an efficient and forwarded in time RL method which can be used to generate approximate online optimal control policies.

ADP has been fruitfully used to develop adaptive optimal controllers for single-agent systems[35]−[39]and multi-agent systems[31],[40]−[48]online in real time.While noticeable progress has been made on ADP in field of distributed control in multi-agent systems,fewer results consider the differential graphical game.In[31],[43]−[47],concepts of ADP and differential graphical game are brought together to find an online optimal solution for distributed tracking control of continuous-time linear systems.

In[31],an online cooperative policy iteration(PI)algorithm is developed for graphical games of continuous-time linear systems by using the actor-critic architecture[49],composed of two neural networks referred to as actor NN and critic NN.A PI algorithm based on integral reinforcement learning technique[35]is proposed in[43]to learn the Nash solution of linear graphical games in real time.In[44],an online PI algorithm is proposed to solve linear differential graphical games in real time.A cooperative PI algorithm is proposed in[45]to solve linear differential graphical games where all players are heterogeneous in their dynamics.The authors in[46]formulate linear output regulation problem in the linear differential graphical game framework.Moreover,an online PI algorithm is proposed in[46]to obtain the solution of coupled HJ equations by using actor-critic structure in real time.An online PI algorithm is provided in[47]to find the solution of coupled Ham ilton-Jacobi-Isaacs(HJI)equations in zero-sum continuous-time linear differential graphical game where the players were influenced by disturbances.In[40],an ADP algorithm was developed to solve differential graphical games of continuous-time nonlinear systems.The authors in[40]solved the problem by using actor-critic architecture.In[31],[40],[43]−[47],the initial admissible control policies are required to guarantee the stability of the differential graphical game.However,finding the set of initial stabilizing control policies for the players is not a direct and simple task.

In[50],the authors proposed an online optimal single network ADP method to solve zero-sum differential game without the requirement of initial stabilizing control policies and[42]extends the results of[50]to obtain the Nash equilibrium of two-player nonzero sum differential game.To our know ledge,there has not been any result on solving theN-player differential graphical games of continuous-time nonlinear systems using single-network ADP without the requirement of initial stabilizing control policies.

In this paper,an online optimal distributed learning algorithm is proposed to approximately solve the coupled HJ equations ofN-player differential graphical game in an online fashion.Each player approximates its optimal control policy using a single-network ADP.The proposed distributed weight tuning laws of critic NNs guarantee the closed-loop stability in the sense of uniform ultimate boundedness(UUB)and convergence of control policies to the Nash equilibrium.By introducing novel distributed local operators in distributed weight tuning laws,the requirement for initial stabilizing control policies is eliminated.

The contributions of the paper are as follows:

1)This paper extends the results of[42],[50]to theN-player differential graphical games of continuous-time nonlinear systems which have more complexity due to the distributed graphical based formulation of the game and the number of players in comparison with the two-player nonzero-sum[42]and zero-sum[50]differential games.Moreover,the stability of the overall closed-loop system is guaranteed.

2)The distributed learning algorithm proposed in this paper employs only one critic network for each player.As results,this algorithm is less computationally demanding and simpler to implement in comparison with[31],[40],[44]−[47],which used actor-critic structure composed of two NNs for each player.

3)By introducing novel distributed local operators in distributed weight tuning laws,in contrast with[31],[40],[43]−[47],there is no more requirement for initial stabilizing control policies.

The paper is organized as follows.The problem formulation ofN-player graphical differential games of nonlinear systems is described in Section II.Section III develops the online optimal distributed learning algorithm to solve theN-player graphical differential games of continuous-time nonlinear systems using single-network ADP.Section IV,presents simulation examples that show the effectiveness of the proposed approach.Finally,the conclusions are drawn in Section V.

II.PRELIMINARIES AND PROBLEM FORMULATION

A.Graphs

Let the topology of the interactions among leader and followers be represented by digraphG(V,Σ),whereV={ν0,ν1,...,νN}is a nonempty finite set ofN+1 nodes andis a set of edges belonging to the product space ofV(i.e.,Denote the edge from nodejto nodeiasγij=(νj,νi).The leader node is denoted byν0and the leader node does not have any incoming edge.There is at least one outgoing edge from the leader node to one of the followersνiin the graphG(i.e.,γi0＞0).We assume that the graph is simple i.e.There are no self-loops or multiple edges.Consider graphG′(V′,Σ′),as the sub-graph ofG,obtained by removing nodeν0and its relating edges.The weighted adjacency matrix of graphG′is denoted by Γ =[γij]∈RN×Nwith;otherwiseγij=0.The set of neighbors of nodeνiand the set of nodes which containsνiin its neighborhood is denoted byand,respectively.The in-degree matrix of graphG′is defined asD=diag(di)∈RN×N,whereis the weighted in-degree of nodeνi.A direct path is an ordered sequence of nodes in the graph.A digraph is said to contain a spanning tree rooted atνi,if there is a directed path from theνito any other nodes in the graph.A digraph is called detail balanced if there exist scalarsτi＞0,τj＞0 such thatτiγij=τjγjifor alli,j∈N[7].

In this paper,a detail balanced digraph containing a spanning tree rooted at the leader node is considered as the players interactions graph in the game.

B.Problem Formulation

Consider a group ofN-players distributed on a directed interaction graph,whose dynamics are described as follows

fori=1,...,N,wherexi(t)∈Rnis the state vector of playeriandui(t)∈Rmis its control input vector.Also consider the leader agent dynamicsx0(t)∈Rngiven by

Assumption 1:f0(x0),fi(xi)andgi(xi)fori=1,...,Nare locally Lipschitz.

Remark 1:Assumption 1 requiresfi(xi(t))+gi(xi(t))uifori=1,...,Nbe locally Lipschitz which is a standard assumption(For instance see[36],[40],[42],[51])to guarantee the uniqueness of the solution of system(1)for any finite initial condition.

The local tracking errorδifor playeri,i=1,...,N,is defined by

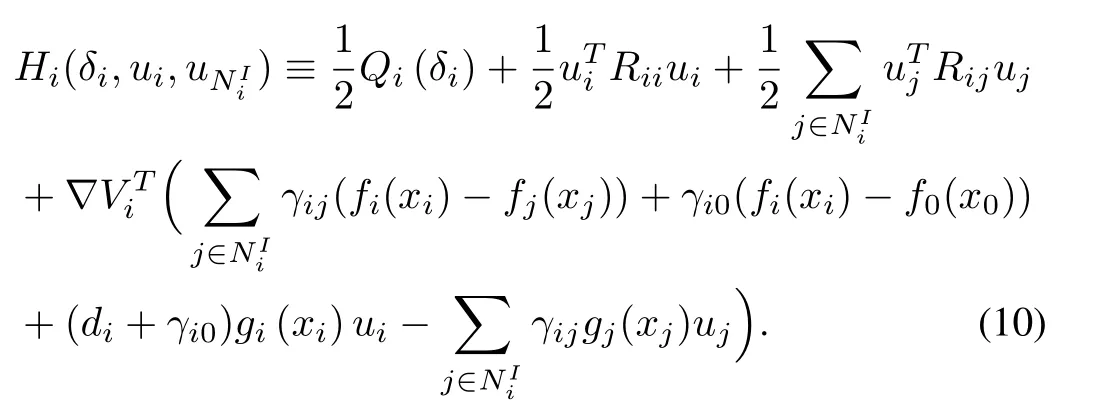
The dynamics of the local tracking error[40]for playeri,i=1,...,N,is given by

Note that,local tracking error dynamics(4)is an interacting dynamical system driven by the control actions of agentiand all of its neighbors.

In differential graphical game,players wish to achieve synchronization while simultaneously optimizing their local cost functions.The distributed local cost function for each playeri,i=1,...,N,is defined by

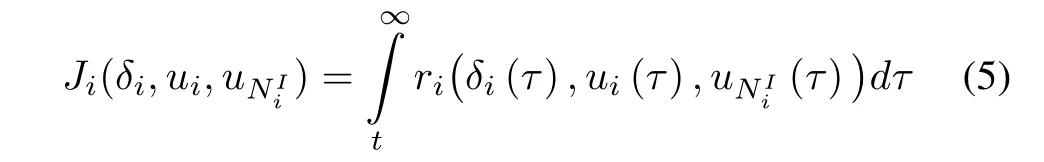
Definition 1[26],[31]:The set of policiesis a global Nash equilibrium solution forN-player differential graphical game if the following inequalities hold for alli,i=1,...,N,and∀ui,uGr−i

whereTheN-tuple of the distributed local cost functionsis known as the Nash equilibrium of the differential graphical game.

Given policies of playeriand its neighbors,the value function for each playeri,i=1,...,N,is given by

In differential graphical game,the goal of playeri,fori=1,...,N,is to determine

The differential equivalent formulation of(7)is given by[40]

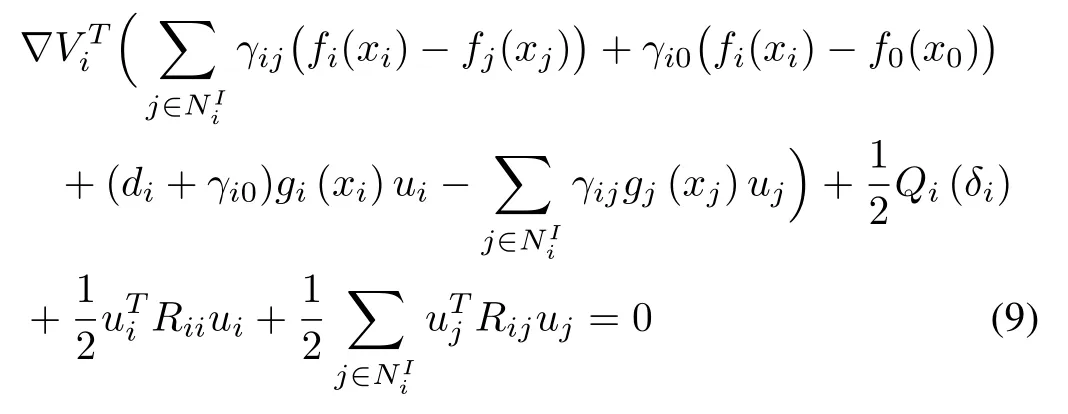
whereVi(0)=0 and

Hamiltonian function for the distributed local cost function of playeri,i=1,...,N,is defined as below

Based on Hamiltonian(10),the optimal feedback control policies can be derived by the stationary condition[52],0,as follows

fori=1,...,N,where the∇Viis the solution of coupled Ham ilton-Jacobi(HJ)equations(12).

Substituting optimal feedback control policy(11)into(10),we have the coupled Ham ilton-Jacobi(HJ)equations fori=1,...,Nas follows

Generally,finding analytical solutions for these coupled HJ equations is difficult or impossible.Therefore,an online optimal distributed learning algorithm is proposed using only single network ADP for each player to solve the coupled HJ equations of(12)in order to obtain the optimal feedback control policies(11)and reach the Nash equilibrium.

Remark 2:The approaches proposed in[50]and[42]cannot be extended directly to solveN-player differential graphical game(11)and(12),due to the distributed graphical based formulation of the game and the number of players.

Before we present the online optimal distributed learning algorithm,the following assumptions and lemma are needed.

Assumption 2:The coupled HJ equations(12)have nonnegative smooth solutionsVi＞0.

Remark 3:The coupled HJ(12)may have non-smooth or non-continuous value functions.However,under Assumption 2,which is a standard assumption in neural adaptive control literature[31],[40]−[42],[51],[53],solutions to the coupled HJ equations(12)are guaranteed to be smooth.This allows us to use the Weierstrass high-order approximation theorem[39],[51,Remark 1].

Assumption 3:For each playeri,there exists a continuously differentiable radially unbounded Lyapunov candidateLi(δi)such that

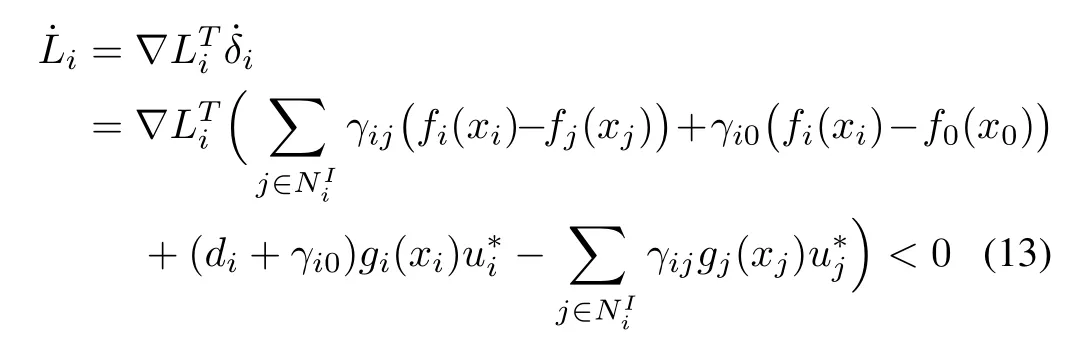
fori=1,...,N,where

Remark 4:The requirement ofLi(δi)being radially unbounded can be fulfilled by its proper choice as quadratic polynomials[42],[50].Although,the existence of continuously differentiable and radially unbounded Lyapunov candidates is not usually required in Lyapunov theory,however their existence have been shown by converse Lyapunov theorems[54].

Lemma 1:Consider the system given by(4)with the distributed local cost functions(7)and optimal feedback control policies(11).Let Assumption 3 holds.Now assume that¯Ciis a positive constant and satisfies the following inequality

then,we have

Proof:By applying optimal feedback control policies(11)to nonlinear systems(4),the distributed local cost function(7)becomes a Lyapunov function.Then,by using Hamiltonian function(10)and differentiating the distributed local cost functionwith respect tot,we obtain

Using(14),we can rewrite(16)as

Finally,by multiplyingto the both sides of(17),we obtain(15),which completes the proof.

III.ONLINE SOLUTION OF N-PLAYER NONLINEAR DIFFERENTIAL GRAPHICAL GAMES USING SINGLE-NETWORK ADP

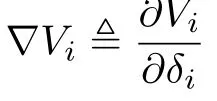
fori=1,...,N,whereK iis the number of hidden-layer neurons of playeri,εi(δi)are the NN approximation errors,are critic NN activation function vectors and

The critic NN activation function vectorsσi(δi)are selected so thatσi(δi)provides complete independent basis sets,fori=1,...,N,such thatσi(0)=0,∇σi(0)=0.The approximation errorsεi(δi)and its gradient∇εi(δi)converge to zero uniformly asK i→∞[55].

Using(19),we can rewrite the optimal feedback control policies(11)and the coupled HJ equations(12),respectively,as follows

fori=1,...,N,where

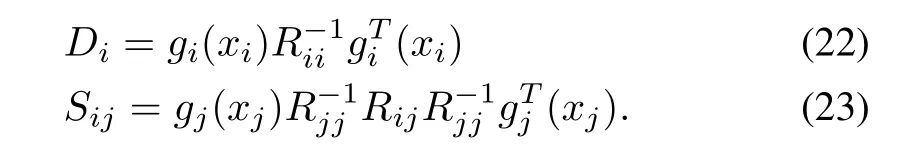
The residual error of playeri,i=1,...,N,in the coupled HJ equations(21),denoted byεHJi,is given by

The weights of the critic NNs,W i,i=1,...,Nare unknown and must be estimated.LetˆWibe the current estimated value ofW ifor each playeri,i=1,...,N.Therefore,the output of every critic NN fori=1,...,Nis

Substituting(25)into(11),we can rewrite the estimates of optimal control policies,fori=1,...,N,as

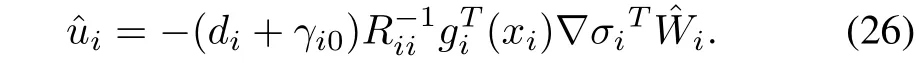
Applying(26)to system(4),yields the closed-loop system dynamics as follows

By replacing(25)and(26)into(10),we obtain the approximate Hamiltonian functions as follows

In order to derive the critic NN weights toward their ideal values i.e.,we utilize normalized gradient descent algorithm to minimize the squared residual error ofeHi,fori=1,...,N.

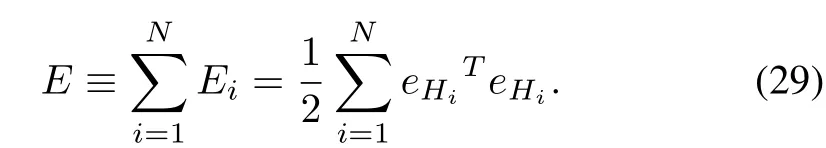
Here,we propose the distributed weight tuning laws of critic NNs(30)forNplayers,which minimize the squared residual error(29)and guarantee the system stability.

fori=1,...,N,where

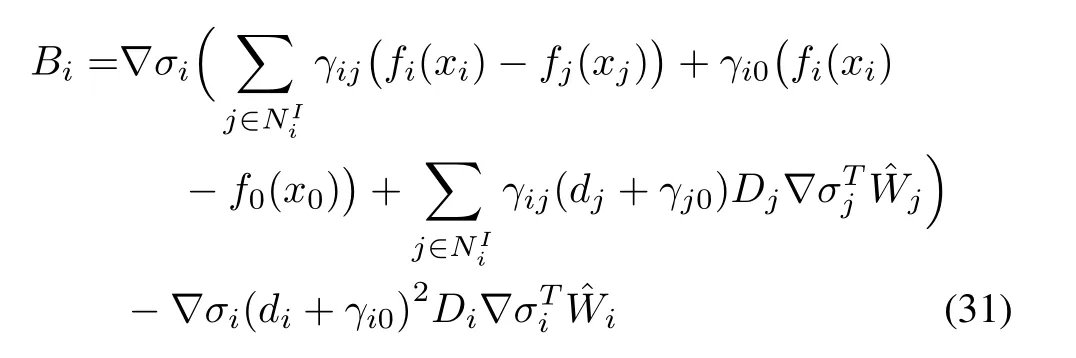
is the learning rate,∇Liis explained in Assumption 3.λi,F1i∈RKi×KiandF2i∈RKi×NKi,fori=1,...,Nare tuning parameters.

The distributed local operators¯χi≡¯χi(S,¯S)andχi≡χi(S,¯S)are defined as follows

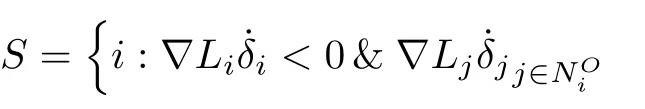
Remark 5:In this paper,each player has its own distributed local operatorsandwhich adopts with distributed nature of differential graphical games problem.Moreover,for each player the introduced distributed local operators only depend on the states of the associated player,its neighbors and the players which the associated player is in their neighborhood.Note that,andimply that the local error dynamics of playeri,its neighbors and the players which the playeriis in their neighborhood are stable.On the other hand,andimply that at least one of the local error dynamics of playeri,its neighbors and the players which the playeriis in their neighborhood is unstable.

Assumption 4:The systems’state given by(4)is persistently excited(PE).

Remark 6:The requirement of PE condition is a standard assumption in adaptive control literature[56].In the adaptive control and learning literature,Assumption 4 is fulfilled by injecting a probing noise into the control input.

The following assumption will be used in the remaining part of the paper.

Assumption 5:

1)gi(xi)are bounded by positive constants,i.e.,‖gi(.)‖≤giM,fori=1,...,N.

2)The critic NN approximation errors and their gradients are bounded by positive constants,i.e.,and,fori=1,...,N.

3)The critic NN activation functions and their gradients are bounded by positive constants,i.e.andσidM,fori=1,...,N.

4)The critic NN weights are bounded by positive constants,i.e.,‖W i‖≤WiM,fori=1,...,N.

5)The residual errorsεHJiare bounded by positive constants,i.e.,‖εHJi‖≤εHJiM,fori=1,...,N.

Remark 7:Assumption 5 is a standard assumption in neural adaptive control literature[39],[41],[42],[53].Although Assumption 5.1 restricts the considered class of nonlinear systems,many practical systems(e.g.,robotic systems[57]and aircraft systems[58])satisfy such a property([31],[40]−[42],[51]for a similar assumption).According to Assumption 2 and the Weierstrass high-order approximation theorem,it is known that the NNs approximation error and their gradient are bounded,i.e.,Assumption 5.2 holds.Note further that,the NNs used in this paper are so-called Functional Link NNs(See[53]for more details),for which activation functionsσifori=1,...,Ncan be some squashing functions,such as the standard sigmoid,Gaussian,and hyperbolic tangent functions.In fact,Assumption 5.5 can be satisfied under Assumptions 2,3 and 5.1−5.4,if Lemma 1 holds.Furthermore,the bounds mentioned above are only used for the stability analysis and they are actually not used in the controller design.

Theorem 1:Let the dynamics be given by(4)and the control policies be given by(26).Let the Assumptions 1−5 hold and the critic NN weight tuning law of each agent be provided by(30).Let the tuning parameters be selected properly.Then,the local tracking error statesδiand the critic NNs weight estimation errors,fori=1,...,Nare UUB,for a sufficiently large number of NN neurons.

Proof:See Appendix A.

Corollary 1:Let the Theorem 1 and Assumptions1−5 hold.Then,the control policiesˆui,fori=1,...,Nform a Nash equilibrium solution.

Proof:See Appendix B.

Remark 8:It can be seen from(54)that by increasingζmin(M)orBZand consequently∈uiare reduced.Therefore,by choosing proper tuning parametersλi,F1iandF2i,we can increaseζmin(M)and reduce the convergence errors∈ui,fori=1,...,N.Also,by choosing properLiin Lemma 1,we can increaseand consequently reduce the convergence errors∈ui,fori=1,...,N.

IV.SIMULATION

Consider a graph of five followers with a leader as shown in Fig.1.In communication graph the pinning gains and the edge weights are chosen to be one.The dynamics of all the followers are expressed by,fori=1,...,5,where

withε=0.5 and the leader dynamics is given as follows

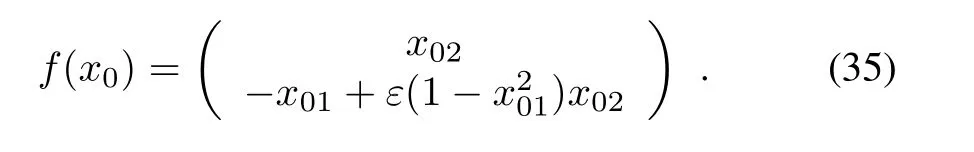
Fig.1.The multi-agent systems communication graph.

Define the distributed local cost functions of followers,fori=1,...,5,as in(5),whereThe learning rates are selected asαi=1,fori=1,...,5.The tuning parameters are selected asF1i=0.1I,F2i=[F11,F12,F13,F14,F15],fori=1,...,5,andλ1=0.6,λ2=10,λ3=10,λ4=0.7,λ5=12.

The critic NN activation functions fori=1,...,5 are chosen as follows

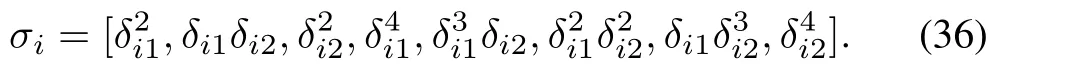
To show that no initial stabilizing control policies are needed for implementing the proposed learning algorithm,all critic NNs weights are initialized to zero.To ensure PE condition,a small exponentially decreasing probing noise is added to control inputs.Figs.2 and 3 show the local tracking errors of followers.

Note that in Figs.2 and 3 the local tracking errors of all followers vanish and all of them synchronize to the leader.Fig.4 shows the phase plane plots of the followers’states.It is shown that in Fig.4 the followers are being synchronized to the leader.

Figs.5 and 6 show the followers critic NN weights convergence.Simulation results show that the proposed learning algorithm can learn the policies which guarantee the synchronization and the closed-loop stability without the requirement for initial stabilizing control policies.

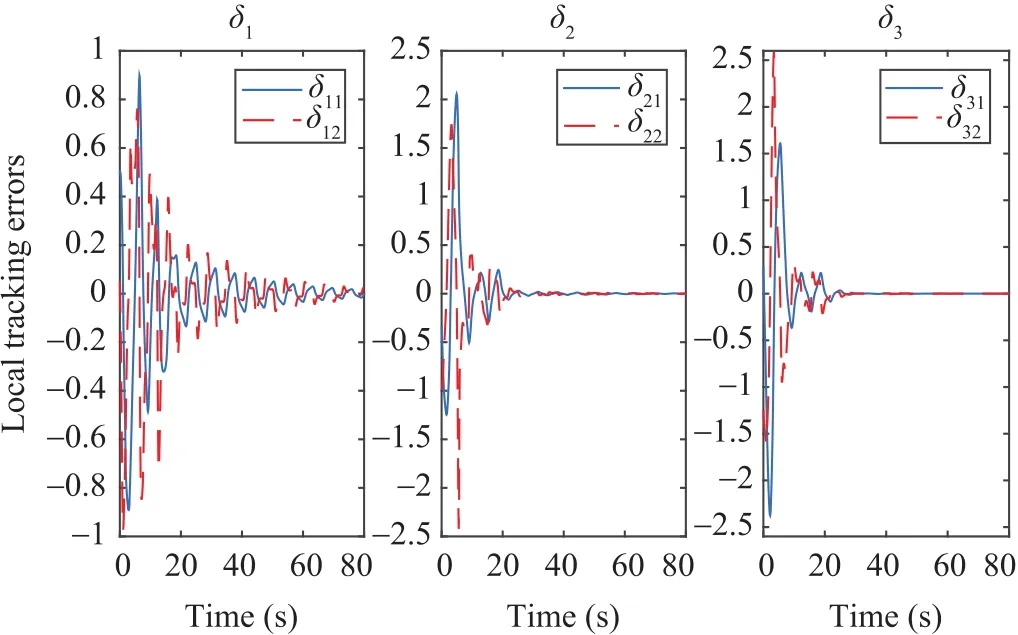
Fig.2.Local tracking errors of the first,second and third followers.

Fig.3.Local tracking errors of the fourth,fifth followers.

Fig.4.The evolution of the followers states.

As we claimed earlier,the proposed scheme has less computational demanding in comparison with the method in[40].To justify our claim,the method in[40]and our method are applied to the systems(34)and(35)with the communication graph as shown in Fig.1.Moreover,initial condition for states and critic NN weights of followers are chosen similarly.The critic NN activation functions fori=1,...,5 are chosen as(36).For the method in[40],the actor NN activation functions arefori=1,...,5.For both methods,One selectfori=1,...,5.For the method in[40],the tuning gains picked all as one.For our method,αi=1 and the tuning parameters are selected asF1i=0.1I,F2i=[F11,F12,F13,F14,F15],fori=1,...,5,andλ1=0.6,λ2=10,λ3=10,λ4=0.7,λ5=12.For comparison of performances,the evaluation functions are defined as follow

fori=1,...,5,whereNSis the number of samples.

Fig.5.Crititc NN weights convergence of the first,second and third followers.

Fig.6.Crititc NN weights convergence of the fourth and fifth followers.

Table I compares the proposed method and the method in[40]regarding the evaluation functions(37)and the amount of time taken by these two methods.As can be seen in Table I,the method proposed in this paper in comparison with the method in[40]has less computational demand and hence it obtains better performance.

TABLE I COMPARISON BETWEEN THE PROPOSED METHOD AND THE ONE PROPOSED IN[40]

V.CONCLUSION

In this paper,an online optimal distributed learning algorithm is developed to solve leader-synchronization problem of nonlinear multi-agent differential graphical games using single network ADP for every agent.The proposed algorithm guarantees the overall closed-loop system stability and convergence of the policies to the Nash equilibrium without the requirement of initial stabilizing control policies.Lyapunov stability theory is employed to show the uniform ultimate boundedness of closed-loop signals of the system.Finally,simulation results show the effectiveness of the proposed algorithm.

For future work,we intend to extend the approach of this paper to obtain the online optimal distributed synchronization control for nonlinear networked systems subject to dynamics uncertainties in the differential graphical games framework.

APPENDIX A PROOF OF THEOREM 1

Take the Lyapunov function

whereLi(δi),fori=1,...,Nare given in Lemma 1.

The derivative of Lyapunov function is given by

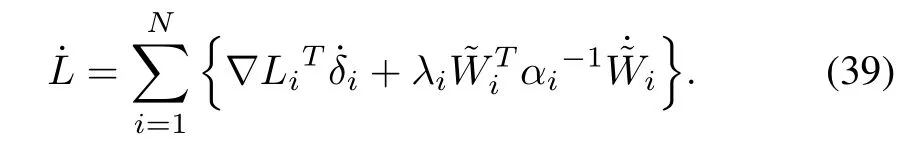
By using(21),(30)and(31),we have

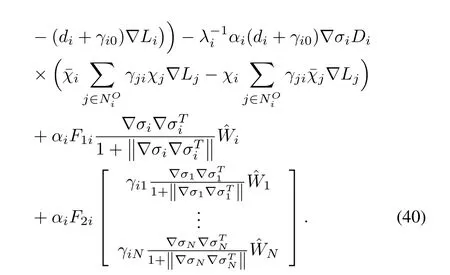
Substituting(40)in(39),yields

whereeij=1,ifγij＞0;otherwiseeij=0.

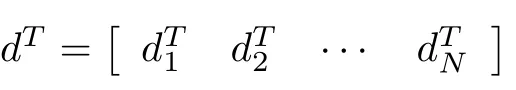
whereIKidenotes the identity matrix of dimensionK i×K iand⊗represents the Kronecker product.Let the tuning parametersλi,F1iandF2i,fori=1,...,Nbe chosen such thatM＞0.

According to Assumption 5 and the fact thatfori=1,...,N,it can be shown that‖d‖≤dMwheredMis a positive constant.Now,(42)becomes

whereζmin(M)is the minimum singular value of matrixM.

Using(11)and(20)as well as adding and subtracting the following terms to the right side of(48),we obtain

By employing Lemma 1,(50)is rewritten as follows

Now,if one of the following inequalities hold

APPENDIX B PROOF OF COROLLARY 1

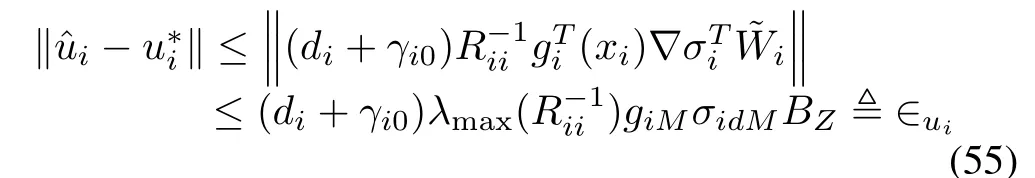
whereis the maximum eigenvalue of matrixThis completes the proof.

[1]R.Olfati-Saber and R.M.Murray,“Consensus problems in networks of agents with switching topology and time-delays,”IEEE Trans.Automat.Control,vol.49,no.9,pp.1520−1533,Sep.2004.

[2]W.Ren and R.W.Beard,“Consensus seeking in multiagent systems under dynamically changing interaction topologies,”IEEE Trans.Automat.Control,vol.50,no.5,pp.655−661,May 2005.

[3]W.Ren and R.W.Beard,Distributed Consensus in Multi-Vehicle Cooperative Control:Theory and Applications.Berlin,Germany:Springer-Verlag,2008.

[4]J.A.Fax and R.M.Murray,“Information flow and cooperative control of vehicle formations,”IEEE Trans.Automat.Control,vol.49,no.9,pp.1465−1476,Sep.2004.

[5]A.Jadbabaie,J.Lin,and A.S.Morse,“Coordination of groups of mobile autonomous agents using nearest neighbor rules,”IEEE Trans.Automat.Control,vol.48,no.6,pp.988−1001,Jun.2003.

[6]Z.H.Qu,Cooperative Control of Dynamical Systems:Applications to Autonomous Vehicles.New York,USA:Springer-Verlag,2009.

[7]F.L.Lew is,H.W.Zhang,K.Hengster-Movric,and A.Das,Cooperative Control of Multi-Agent Systems:Optimal and Adaptive Design Approaches.Berlin,Germany:Spring-Verlag,2014.

[8]M.Defoort,T.Floquet,A.Kokosy,and W.Perruquetti,“Sliding-mode formation control for cooperative autonomous mobile robots,”IEEE Trans.Ind.Electron.,vol.55,no.11,pp.3944−3953,Nov.2008.

[9]J.Mei,W.Ren,and G.F.Ma,“Distributed containment control for Lagrangian networks with parametric uncertainties under a directed graph,”Automatica,vol.48,no.4,pp.653−659,Apr.2012.

[10]W.Lin,“Distributed UAV formation control using differential game approach,”Aerosp.Sci.Technol.,vol.35,pp.54−62,May 2014.

[11]R.Abdolee,B.Champagne,and A.H.Sayed,“Diffusion adaptation over multi-agent networks with wireless link impairments,”IEEE Trans.Mobile Comput.,vol.15,no.6,pp.1362−1376,Jun.2016.

[12]W.Q.Wang,“Carrier frequency synchronization in distributed wireless sensor networks,”IEEE Syst.J.,vol.9,no.3,pp.703−713,Sep.2015.

[13]S.M.Mu,T.G.Chu,and L.Wang,“Coordinated collective motion in a motile particle group with a leader,”Phys.A,vol.351,no.2−4,pp.211−226,Jun.2005.

[14]V.Nasirian,S.Moayedi,A.Davoudi,and F.L.Lew is,“Distributed cooperative control of DC microgrids,”IEEE Trans.Power Electron.,vol.30,no.4,pp.2288−2303,Apr.2015.

[15]L.L.Fan,V.Nasirian,H.Modares,F.L.Lew is,Y.D.Song,and A.Davoudi, “Game-theoretic control of active loads in DC microgrids,”IEEE Trans.Energy Convers.,vol.31,no.3,pp.882−895,Sep.2016.[16]D.M.Xie and J.H.Chen,“Consensus problem of data-sampled networked multi-agent systems with time-varying communication delays,”Trans.Inst.Meas.Control,vol.35,no.6,pp.753−763,Mar.2013.

[17]S.Y.Tu and A.H.Sayed,“Diffusion strategies outperform consensus strategies for distributed estimation over adaptive networks,”IEEE Trans.Signal Process.,vol.60,no.12,pp.6217−6234,Dec.2012.

[18]H.W.Zhang,F.L.Lew is,and Z.H.Qu,“Lyapunov,adaptive,and optimal design techniques for cooperative systems on directed communication graphs,”IEEE Trans.Ind.Electron.,vol.59,no.7,pp.3026−3041,Jul.2012.

[19]W.Ren,R.W.Beard,and E.M.Atkins,“Information consensus in multivehicle cooperative control,”IEEE Control Syst.,vol.27,no.2,pp.71−82,Apr.2007.

[20]Z.J.Tang,“Leader-following consensus with directed switching topologies,”Trans.Inst.Meas.Control,vol.37,no.3,pp.406−413,Jul.2015.

[21]A.R.Wei,X.M.Hu,and Y.Z.Wang,“Tracking control of leader follower multi-agent systems subject to actuator saturation,”IEEE/CAA J.Automat.Sin.,vol.1,no.1,pp.84−91,Jan.2014.

[22]C.H.Zhang,L.Chang,and X.F.Zhang,“Leader-follower consensus of upper-triangular nonlinear multi-agent systems,”IEEE/CAA J.Automat.Sin.,vol.1,no.2,pp.210−217,Apr.2014.

[23]C.R.Wang,X.H.Wang,and H.B.Ji,“A continuous leader-following consensus control strategy for a class of uncertain multi-agent systems,”IEEE/CAA J.Automat.Sin.,vol.1,no.2,pp.187−192,Apr.2014.

[24]Y.G.Hong,J.P.Hu,and L.X.Gao,“Tracking control for multi-agent consensus with an active leader and variable topology,”Automatica,vol.42,no.7,pp.1177−1182,Jul.2006.

[25]G.Owen,Game Theory.New York,USA:Academic Press,1982.

[26]T.Basar and G.J.Olsder,Dynamic Noncooperative Game Theory(Classics in Applied Mathematics).Philadelphia,PA,USA:SIAM,1999.

[27]E.Semsar-Kazerooni and K.Khorasani,“Multi-agent team cooperation:A game theory approach,”Automatica,vol.45,no.10,pp.2205−2213,Oct.2009.

[28]C.X.Jiang,Y.Chen,and K.J.R.Liu,“Distributed adaptive networks:A graphical evolutionary game-theoretic view,”IEEE Trans.Signal Process.,vol.61,no.22,pp.5675−5688,Nov.2013.

[29]C.X.Jiang,Y.Chen,Y.Gao,and K.J.R.Liu,“Indian buffet game with negative network externality and non-Bayesian social learning,”IEEE Trans.Syst.Man Cybern.Syst.,vol.45,no.4,pp.609−623,Apr.2015.

[30]R.Kamalapurkar,J.R.Klotz,and W.E.Dixon,“Concurrent learning based approximate feedback-Nash equilibrium solution of N-player nonzero-sum differential games,”IEEE/CAA J.Automat.Sin.,vol.1,no.3,pp.239−247,Jul.2014.

[31]K.G.Vamvoudakis,F.L.Lew is,and G.R.Hudas,“Multi-agent differential graphical games:Online adaptive learning solution for synchronization with optimality,”Automatica,vol.48,no.8,pp.1598−1611,Aug.2012.

[32]R.S.Sutton and A.G.Barto,Reinforcement Learning:An Introduction.Cambridge,MA,USA:M IT Press,1998.

[33]P.J.Werbos,“Approximate dynamic programming for real-time control and neural modeling,”Handbook of Intelligent Control,D.A.White and D.A.Sofge,Eds.New York,USA:Van Nostrand Reinhold,1992.

[34]J.J.Murray,C.J.Cox,G.G.Lendaris,and R.Saeks,“Adaptive dynamic programming,”IEEE Trans.Syst.Man Cybern.C,vol.32,no.2,pp.140−153,May 2002.

[35]H.Modares,F.L.Lew is,and M.B.Naghibi-Sistani,“Integral reinforcement learning and experience replay for adaptive optimal control of partially-unknown constrained-input continuous-time systems,”Automatica,vol.50,no.1,pp.193−202,Jan.2014.

[36]H.Modares and F.L.Lew is,“Optimal tracking control of nonlinear partially-unknown constrained-input systems using integral reinforcement learning,”Automatica,vol.50,no.7,pp.1780−1792,Jul.2014.

[37]Z.P.Jiang and Y.Jiang,“Robust adaptive dynamic programming for linear and nonlinear systems:An overview,”Eur.J.Control,vol.19,no.5,pp.417−425,Sep.2013.

[38]S.Bhasin,R.Kamalapurkar,M.Johnson,K.G.Vamvoudakis,F.L.Lew is,and W.E.Dixon,“A novel actorCcriticCidentifier architecture for approximate optimal control of uncertain nonlinear systems,”Automatica,vol.49,no.1,pp.82−92,Jan.2013.

[39]K.G.Vamvoudakis and F.L.Lew is,“Online actor-critic algorithm to solve the continuous-time infinite horizon optimal control problem,”Automatica,vol.46,no.5,pp.878−888,May 2010.

[40]F.Tatari,M.B.Naghibi-Sistani,and K.G.Vamvoudakis,“Distributed learning algorithm for non-linear differential graphical games,”Trans.Inst.Meas.Control,Vol 39,no.2,pp.173−182,Feb.2017.

[41]K.G.Vamvoudakis and F.L.Lew is,“Multi-player non-zero-sum games:Online adaptive learning solution of coupled Hamilton-Jacobi equations,”Automatica,vol.47,no.8,pp.1556−1569,Aug.2011.

[42]H.G.Zhang,L.L.Cui,and Y.H.Luo,“Near-optimal control for nonzero-sum differential games of continuous-time nonlinear systems using single-network ADP,”IEEE Trans.Cybern.,vol.43,no.1,pp.206−216,Feb.2013.

[43]M.I.Abouheaf and F.L.Lew is,“Multi-agent differential graphical games:Nash online adaptive learning solutions,”inProc.52nd Annu.Conf.Decision and Control.Firenze,Italy,2013,pp.5803−5809.

[44]M.I.Abouheaf,F.L.Lew is,and M.S.Mahmoud,“Differential graphical games:Policy iteration solutions and coupled Riccati formulation,”inProc.2014 European Control Conf..Strasbourg,France,2014,pp.1594−1599.

[45]Q.L.Wei,D.R.Liu,and F.L.Lew is,“Optimal distributed synchronization control for continuous-time heterogeneous multi-agent differential graphical games,”Inform.Sci.,vol.317,pp.96−113,Oct.2015.

[46]F.A.Yaghmaie,F.L.Lew is,and R.Su,“Output regulation of heterogeneous linear multi-agent systems with differential graphical game,”Int.J.Robust Nonlinear Control,vol.26,pp.2256−2278,Jul.2016.

[47]Q.Jiao,H.Modares,S.Y.Xu,F.L.Lew is,and K.G.Vamvoudakis,“Multi-agent zero-sum differential graphical games for disturbance rejection in distributed control,”Automatica,vol.69,pp.24−34,Jul.2016.

[48]M.I.Abouheaf,F.L.Lew is,K.G.Vamvoudakis,S.Haesaert,and R.Babuska,“Multi-agent discrete-time graphical games and reinforcement learning solutions,”Automatica,vol.50,no.12,pp.3038−3053,Dec.2014.

[49]A.G.Barto,R.S.Sutton,and C.W.Anderson,“Neuronlike adaptive elements that can solve difficult learning control problems,”IEEE Trans.Syst.Man Cybern.,vol.SMC-13,no.5,pp.834−846,Sep.−Oct.1983.

[50]T.Dierks and S.Jagannathan,“Optimal control of affine nonlinear continuous-time systems using an online Hamilton-Jacobi-Isaacs formulation,”inProc.49th Conf.Decision and Control.Atlanta,GA,USA,2010,pp.3048−3053.

[51]M.Abu-Khalaf and F.L.Lew is,“Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach,”Automatica,vol.41,no.5,pp.779−791,May 2005.

[52]F.L.Lew is,D.Vrabie,and V.L.Syrmos,Optimal Control.Hoboken,NJ,USA:John Wiley,2012.

[53]F.L.Lew is,S.Jagannathan,and A.Yes¸ildirek,Neural Network Control of Robot Manipulators and Nonlinear Systems.London,UK:Taylor and Francis,1999.

[54]H.K.Khalil,Nonlinear Systems.Englewood Cliffs,New Jersey,USA:Prentice-Hall,1996.

[55]B.A.Finlayson,The Method of Weighted Residuals and Variational Principles.New York,USA:Academic Press,1990.

[56]P.Ioannou and B.Fidan.Adaptive Control Tutorial(Advances in Design and Control).Philadelphia,PA:SIAM,2006.

[57]J.J.E.Slotine and W.P.Li,Applied Nonlinear Control.Englewood Cliffs,NJ,USA:Prentice Hall,1991.

[58]S.Sastry and M.Bodson,Adaptive Control:Stability,Convergence,and Robustness.Englewood Cliffs,NJ:Prentice Hall,1989.