Encoding-Decoding-Based Control and Filtering of Networked Systems:Insights,Developments and Opportunities

Zidong Wang,Fellow,IEEE,Licheng Wang,Shuai Liu,and Guoliang Wei

I.INTRODUCTION

A.Engineering Insights

I T has been well recognized that the publication titled“A Mathematical Theory of Communication”[112],[113]by C.E.Shannon in 1948 marked the establishment of the

Z.Wang is with the Department of Computer Science,Brunel University London,Uxbridge,Middlesex,UB8 3PH,United Kingdom.(e-mail:Zidong.Wang@brunel.ac.uk).

L.Wang and G.Wei are with the Department of Control Science and Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China.(e-mail:wanglicheng1217@163.com;guoliang.wei1973@gmail.com).

S.Liu is with the Business School,University of Shanghai for Science and Technology,Shanghai 200093,China.(e-mail:liushuai871030@163.com).

Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.

Digital Object Identifier 10.1109/JAS.2017.7510727 information theory.From then on,constant research effort from the researchers of different fields has been put on its developments and considerable progress has been made in the aspects of theory and application.Coincidentally,in the same year,another celebrated mathematician N.Wiener published his famous treatise“Cybernetics:Or Control and Communication in the Animal and the Machine”[133],which laid down the theoretical foundation for the servomechanisms(whether electrical,mechanical or hydraulic),automatic navigation,analog computing,artificial intelligence,neuroscience and reliable communications,and made the birth of control theory.Nevertheless,during the past few decades,the information theory and control theory have almost been regarded as two independent disciplines with few common features and connections due to their different concerns.

Broadly speaking,the information theory mainly focuses on how to obtain,store,process and transmit the data but seldom pays attention to the specific usage of the data itself.On the contrary,the control theory concerns how to make use of the obtained data to achieve the prescribed tasks through certain strategies.For general systems,the most basic but important idea to realize desirable system performances is the “feedback”,which means the obtained signals(usually the system outputs)should be fed back to the systems’inputs in certain manners by designing proper feedback mechanisms.However,in most cases,such an idea is usually implemented upon the assumption that the signal transmission between the components is with in finite precision,namely,the signals can be perfectly transmitted and utilized to contribute to the feedback schemes.

In recent years,owing to the rapid development of the networked communication technology,the networked systems(NSs)have emerged as a new yet popular system architecture with an extensive utilization in the industry for its low power cost,simple installation,easy maintenance and high reliability.Different from the non-networked systems where the data flows through the components in a point-to-point way,the NSs mean that all the data communications between the components are executed via a commonly shared communication network(channel).Although the NSs possess various merits mentioned above,the introduction of the communication network also brings about some new and noteworthy problems including 1)how the network-based data exchange affects the system performance,and 2)how to maximize the utilization of limited network bandwidth while ensuring the required system performance.

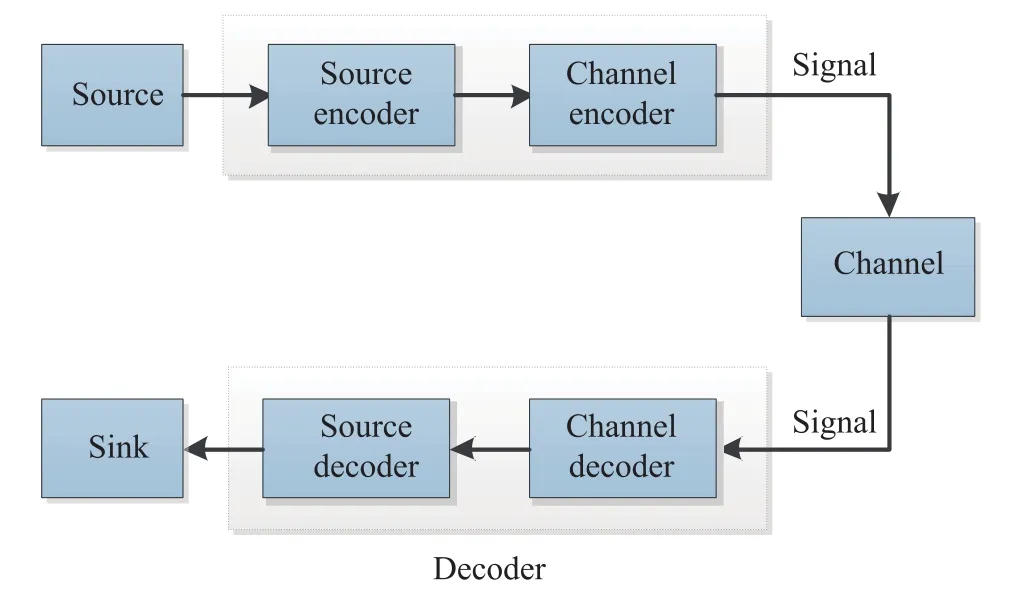
Fig.1.Structure of the general communication system.

If the network environment is ideal,that is,the bandwidth of the network is sufficiently large,the assumption of the perfect data transmission would make sense and it is reasonable to ignore the influence from the network communication on the system performance.However,in the situations that the network resources are subject to certain constraints(e.g.,limited bandwidth of the channel),it is no longer proper to entirely neglect the distortion of the transmitted data caused by the limited communication capacity of the network.Especially,when it comes to the large-scale NSs such as wireless sensor networks(WSNs),multi-agent systems(MASs)and smart grids,the limited network resources impose severe restrictions on the data communication quality and even deteriorate the overall system performances.On the other hand,from the standpoint of the network security,the NSs are usually fragile and vulnerable to be attacked,e.g.,the data flowing through the system components are easily stolen by the adversaries for some hostile purposes,see[15],[39],[76],[143].Therefore,in order to make the data transmission of the NSs more efficient and secure via a resource-constrained communication network,the encoding-decoding technique stands out as an ideal candidate for its advantage in data compression and encryption.

B.Theoretical Outlines

Normally,as shown in Fig.1,a classic communication system always contains three basic parts:the information source,the information channel and the information sink,based on which,the encoding-decoding technique can be accordingly divided into two main categories:the source encoding-decoding and the channel encoding-decoding.In this paper,our attention will be specifically focused on the source encoding-decoding technique,which aims to transform the original data into certain codewords.Generally speaking,the source information encoding technique possesses the following three prominent features:1)realizing the data compression,2)facilitating the digital data transmission,and 3)enhancing the data security.From the aspect of mathematics,the process of encoding can be regarded as a mapping that maps the original data to certain codewords.Correspondingly,the decoding process can be viewed as the “inverse”operation which intends to recover the original data as exactly as possible by excavating the information contained in the codewords.To be more specific,in the networked communication systems,letx(k),F(·),andxd(k)be the original signal before being encoded,the encoding mapping,the encoding alphabet,the decoding mapping,and the decoded signal,respectively,wherekis the discrete time step and theis a set whose elementssi(i=1,2,...,m)are certain deterministic codewords.In most existing literature,the authors’attempts have always been made to design a pair of encoder-decoder appropriately such that at each time instantk,the decoding erroris possibly small at the minimum cost of the network bandwidth.

In view of the aforementioned discussion,it is obvious that there are two important performance indices to evaluate the designed encoding-decoding procedure,namely,the decoding error and the bandwidth condition.Intuitively,the large network bandwidth would result in a small decoding error.For the NSs,if the network resource is not the concern(e.g.,the bandwidth can be sufficiently large),the decoding error would probably be very small and hence has little impact on the system performance.In this case,the coding-decoding-based NSs reduce to the traditional NSs for the analysis and synthesis issues.However,in most practical situations,due to the limited network resources,the network bandwidth serving as a major concern should be incorporated into the system design.In this sense,for the bandwidth-constrained systems,the concept of“minimum bit rate”is proposed to characterize the smallest needed channel capacity for the codeword transmission,above which the performance of the controlled(or filtering error)systems is explored including asymptotical/exponential stability,ultimately bounded stability,input-to-state stability(ISS),etc.

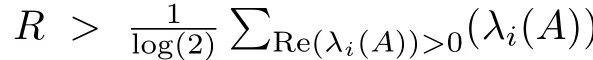
Compared with the traditional NSs,the introduction of the encoding-decoding communication mechanism would make the dynamics of the NSs more complicated and diverse,which accordingly imposes certain challenges on the analysis and synthesis issues.Moreover,because of the inevitable data distortion resulted from the encoding-decoding process,the traditional approaches cannot be directly generalized to cope with the performance analysis issues of encoding-decodingbased NSs.In this case,the influence of the encoding-decoding mechanism on the system performance should be well taken into consideration.In other words,how to choose suitable theoretical tools to quantitatively evaluate the relationship between the system dynamics and the encoding-decoding communication protocol appears to be particularly important.To date,there are generally three theoretical methodologies to deal with the encoding-decoding-based analysis and synthesis problems for the NSs,namely,the information-theory-based methodology,the ISS-based methodology and the hybridsystem-based methodology.

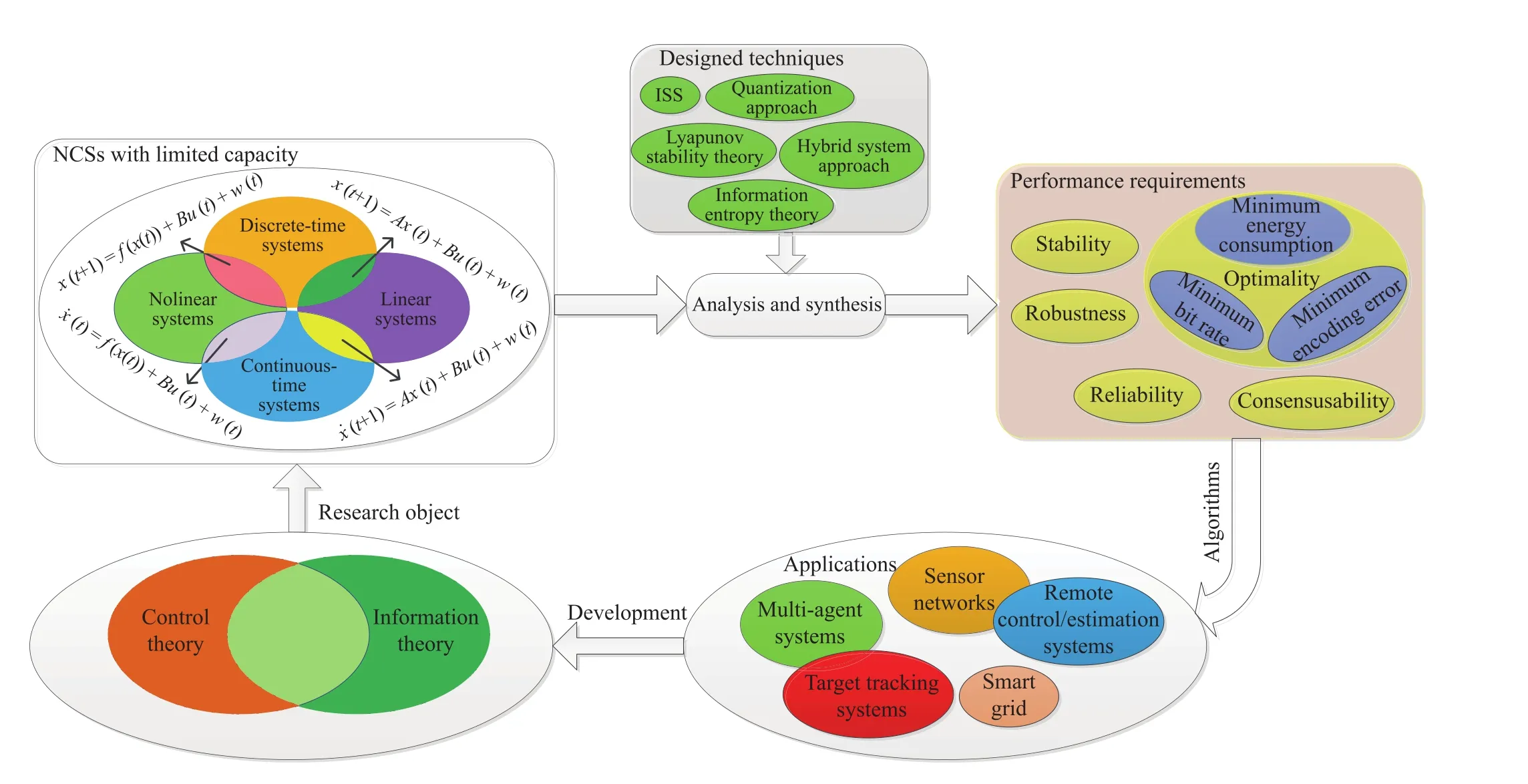
Fig.2.Framework of surveyed contents.

The theoretical basis of the information theory methodology is the celebrated Shannon information theory,based on which,all information including the original data,codewords and decoded data are described as random variables[23],[24],[92].Within such a framework,the main objective is to find general necessary conditions for the channel capacity measured by the concept of “entropy”,under which the original data can be reconstructed from the decoded data with the acceptable distortion.Then,by resorting to the decoded data,the desired control or filtering performance can be guaranteed.On the other hand,for most of the effective encoding schemes,a basic requirement is that the decoding errored(k)should be bounded or even convergent.Thus,it is natural to view the decoded error as the bounded disturbance of the dynamical system,and the ISS-based approach[69],[98]has been proposed as a theoretical tool to handle the analysis and synthesis issues for these systems.For the continuous-time systems with a digital transmission manner,the received codewords by the decoder at a certain discrete instant can be seen as an impulse sequence that affects the decoder dynamics.Consequently,the hybrid-system-based approach[68],[70]is valid for analyzing such a kind of systems’dynamical behaviors.

In this paper,our purpose is to offer an up-to-date review of existing research results on encoding-decoding-based control and filtering problems for the NSs.Various usually adopted design schemes of the encoding-decoding procedure in the NSs and their individual characteristics are reviewed.Subsequently,recent advances on the encoding-decoding-based control and filtering problems for the NSs are,respectively,surveyed.Then,the control and filtering issues for distributed systems with encoding-decoding communication scheme are discussed.Finally,conclusions and future research directions are presented.The main contents that are reviewed in this paper and the framework are shown in Fig.2.

II.MA IN ENCODING-DECODING SCHEMES IN NSS

In the framework of the coding-decoding-based data communications for NSs,it is of crucial importance to construct a suitable pair of encoder and decoder which could greatly restrain the impacts from the resulted data distortion on the system performance.To this end,we are going to give a clear look on some commonly utilized encoding-decoding schemes with the following system model

or

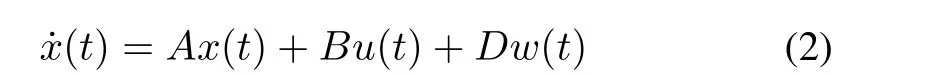
with the measurement output

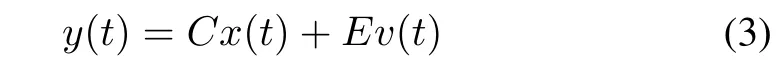
wherex(t)∈Rnx,u(t)∈Rnu,andy(t)∈Rnyare,respectively,the system state,the system input,and the measurement output.w(t)∈Rnwandv(t)∈Rnvare the process and the measurement noises.A,B,C,D,andEare the known matrices with compatible dimensions.For analysis convenience,in this paper,it is assumed that the system statex(t)is accessible for the stabilization problem,while for the filtering issue,it is supposed that only the measurement outputy(t)is observable.Till now,in the existing literature,two representative design solutions of the encoding-decoding procedure have been proposed to deal with the control and filtering problems in the NSs,namely,the quantization-based encoding-decoding technique and the symbolic-based encoding-decoding technique.Several typical encoding-decoding schemes in the NCSs are exhibited in Fig.3.In the following,we are in a position to successively illustrate these encoding-decoding design approaches mentioned above.

Fig.3.The summarization of several typical encoding-decoding schemes in NCSs.

A.Quantization-Based Encoding-Decoding Mechanism

The quantization-based encoding-decoding method is one of the most common methods for the NSs with the limited communication capacity,based on which,a number of coderdecoder structures have been presented in the existing literature,see[47],[56],[65],[111],[148].In addition,according to the case whether the quantizer parameters can be dynamically adjusted,the quantizer can be classified into the static quantizer and the dynamic one.In the following,in terms of the type of the used quantizer,three typical coder-decoder structures are listed and their corresponding characteristics are summarized.

1)Dynamic-quantization-based encoding-decoding scheme I:Such a method was proposed in[111]and the similar idea appeared in the earlier literature[67].For the sake of making this approach more understandable, first,let us briefly recall some basic concepts of the uniform quantization,and then we will show how the uniform quantization approach is applied to the encoder-decoder procedure.

Let the scaling parameter(the length of the quantization interval)a＞0 and integerqbe given,and theBadenotes the hyperrectangle in Rncentered at 0 with the edge lengtha,i.e.,,where|·|∞is the in finite vector norm.Then,we uniformly partition the hyperrectanglesBaintoqnsub-hyperrectangleswheres1,s2,...,sn∈{1,2,...,q}and

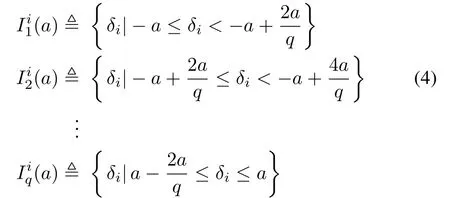
whereδiis theith element of the vectorδ.Here,each subhyperrectangleis labeled with a sequence{s1,s2,...,sn},which represents the specific region of the sub-hyperrectangle and will be sent to the decoder for the reconstruction of the original data.Moreover,the center of the sub-hyperrectanglecan be defined as

where

In what follows,we employ the proposed encodingdecoding protocol to the continuous-time system(2)for the stabilization problem.To be more specific,our goal is to design a pair of encoder-decoder and certain decoded-signalbased control strategy such that the closed-loop system is asymptotically stable.For simplicity of the illustration,we assume that the disturbancew(t)in(2)satisfiesw(t)≡0 and the main idea for the design of the encoding-decodingbased control strategy can be outlined with the following steps.To start with,at each encoding timejT(j=1,2,...and“T”is the encoding period),by calculating the errore(jT)between the system statex(jT)and the decoded statewhich will be defined later,wherewe are able to determine the uniform quantization parameter “a”and thus partition the hyperrectangleBaintoqnequal sub-hyperrectangles.Here,denotes the limit ofat the point ofjTfrom the left,i.e.,Subsequently,generate the corresponding codeword sequence{s1,s2,...,sn}according to the region where the error“e(jT)”belongs to and then transmit the codeword sequence{s1,s2,...,sn}to the decoder to obtain the decoded state.Finally,design the controller“u(jT)”in terms of the decoded stateto stabilize the original system.

Based on the above analysis,the detailed form of the encoder and decoder is given as follows:

Coder:Forwe have

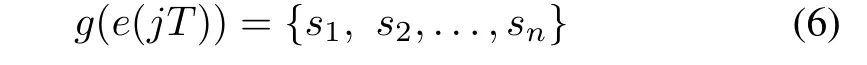
wherea((j+1)T)=ϕ(T,q,x(0))a(jT)forj=1,2,...withϕ(T,q,x(0))being the function of certain form with respect to the encoding periodT,the quantization levelqand the initial conditionx(0).

Decoder:

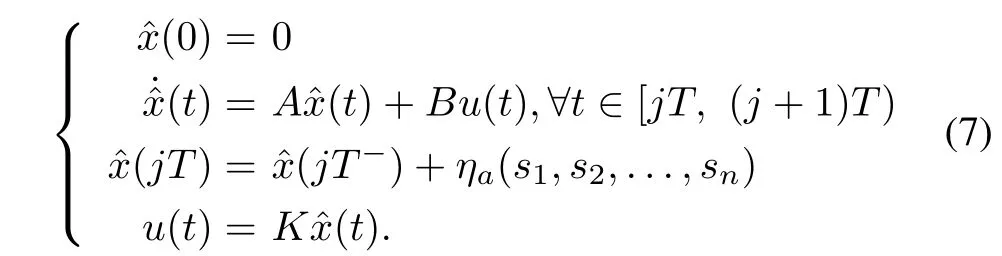
From structures of the coder(6)and the decoder(7),we have the following observations.1)The proposed encoding approach is a kind of differential encoding technique.It is obvious that,in(6),only the decode errore(jT)is encoded at the encoding timejT.In fact,by using the differential quantization encoding technique to encode the signal difference,the amount of the information to be sent is greatly reduced,see[22].2)It can be seen from the iteration relationship betweena((j+1)T)anda(jT)that the quantization region dynamically varies at each encoding instant,and such a quantizer is referred to as the dynamic quantizer.3)In order to enforce the decoding error be convergent,it is required thatϕ(T,q,x(0))＜1,from which,we can see that the convergence of the encoding-decoding algorithm is closely associated with the encoding period,the quantization level and the initial condition of the system.

Apart from the continuous-time case,for the discrete-time counterpart,the encoding-decoding communication strategy for the NSs has been considered in[148],and the corresponding extended control/ filtering problems subject to the networkinduced phenomena have been investigated in[126],[136].

2)Dynamic-quantization-based encoding-decoding scheme II:This kind of encoding-decoding scheme is based on the so-called “zooming in/zooming out”quantization technique which was proposed in[134].For the discrete-time system(1)withw(t)≡0,the following encoder is given by

whereξ(t)is the encoder’s internal state,s(t)is the generated codeword which needs to be sent to the decoder,Q(·)is a finite-level uniform quantizer,andg(t)is a scaling function which is used to adjust the amplitude of the signal to be quantized.In most of the literature,the quantizerQ(·)is chosen as the symmetric one with the following form

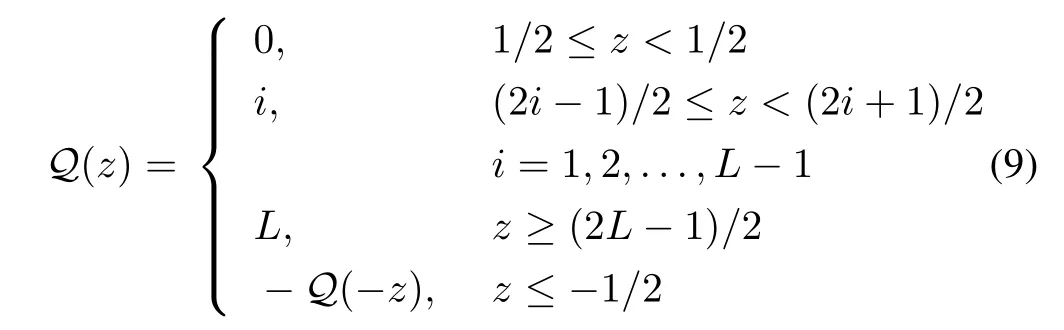
whereLis the quantizer’s saturation value and the associated quantization level is 2L+1.

By using the generated codewords(t),the decoder Ψ is designed as

whereis the output of the decoder,namely,the decoded value.

It can be concluded from the structure of the above encoderdecoder that 1)although the saturation valueLis fixeda priori,due to the introduction of the scaling functiong(t),the signal to be quantized is enforced to be pre-processed first by the “zooming out”or “zooming in”technique,and hence this type of encoding approach is still of the dynamic quantization-based encoding,2)as discussed above,encoding the difference betweenx(t)andξ(t−1)with scaling rather than the system statex(t)itself possibly reduces the bits which are utilized to represent the codeword,3)the saturation valueLis closely related to the network bandwidth,that is,a smallLresults in the requirement of a small network bandwidth.Especially,whenL=1,it means that only one bit is necessary to send the codeword,and 4)the encoding period is consistent with the system sampling period,which is different from the former encoding approach that the encoding period can be the multiple of the system sampling period,see[111],[136],[148].

Such a “zooming in/zooming out” quantization-based encoding-decoding scheme was first proposed in[5],under which,a consensus algorithm has been designed for a class of discrete-time MASs that the information exchange among the agents was implemented through a digital communication network.Recently,some extensions have emerged,see[54],[57],[64],[65],[140],however,most of which are concerned with the discrete-time systems and the results for the continuoustime counterpart are relatively few.

3)Static-quantization-based encoding-decoding scheme:Having presented the above two different kinds of encodingdecoding schemes,now we would like to give a simple discussion about another encoding-decoding scheme,namely,the multiple description(MD)encoding-decoding scheme.The original idea of the MD encoding-decoding scheme comes from the investigation of the audio encoding issue in the telephone network by Bell Laboratories in the 1970s.As the rapid development of the network-based(e.g.internet)communication techniques,in recent decades,the MD encoding-decoding technology has gained considerable research attention from many researchers in different disciplines.

The idea of the MD encoding-decoding scheme is based on the diversity principle which could effectively enhance the transmission capacity and reliability of the channels,see[18],[30],[47],[121],[122].From the point of the information theory view,the diversity principle can be understood as follows:encode the information source into multiple descriptions with the identical importance and then sent to the decoder via the parallel individual channel.The framework of the MD encoding-decoding scheme is built on the following two assumptions:1)there are multi-channels between the encoder and the decoder and all the channels failing to work simultaneously is a small probability event,and 2)the original signal can be reconstructed with an acceptable quality as long as at least one of the descriptions is successfully delivered to the decoder,and when more descriptions are received by the decoder,the signal is reconstructed with a higher quality.Therefore,such an approach is able to improve the transmission reliability by rejecting the channel fluctuations resulted from the fading[37],shadowing,crosstalk,etc.

So far,according to the adopted method in the encodingdecoding process,the multiple description encoding-decoding can be classified into various classes including multiple description quantization coding(MDQC),the multiple description transformation coding(MDTC),the forward-errorcorrection-based multiple description coding(FECMDC),etc.In this paper,our attention is focused on the MDQC where the static uniform quantization method is applied to the addressed encoding-decoding issue.

Loosely speaking,the static uniform quantizer-based multiple description coding procedure can be divided into two steps.The first step is the index generation process which mainly employs the scalar quantizer to transform the information source into certain indices.Then,represent the indices by multiple descriptions in term of a proper index assignment strategy.For convenience,a brief view on the encoding scheme with two descriptions is provided where the measurement output(3)is treated as the information source to be encoded.The diagram of the MDC for the NSs with two descriptions is shown in Fig.4.

Fig.4.Multiple description encoding-based data communication in NSs.

Encoder:

Decoder:

wheref1l(·)andf2l(·)are two coding functions whose outputsθl(t)andϑl(t)can be regarded as the individual descriptions of the sourceyl(t)withyl(t)being thelth component ofy(t).g1l(·)andg2l(·)are two side decoding functions andgcl(·,·)is the central decoding function.λi(t)(i=1,2)are two independent random variables characterizing the packet dropout phenomena during the transmissions of the individual description,which satisfy the Bernoulli binary distribution taking values on either 1 or 0 with mathematical expectationsand variances,respectively.

The early research effort on the MDC was mainly devoted to its theoretical research.Since the scalar quantization-based MDC method was first proposed in[121],the research direction has been moved from the pure theoretical investigation to its practical applications.From then on,the MDC has experienced a huge development in the theory and applications,and myriad coding schemes have appeared.It should be pointed out that most results of the MDC have been centered on the applications in distributed storage systems[48],diversity communication system(antenna diversity)[106],image/audio/video encoding[2],[4],[9],[137].However,to the best of the authors’know ledge,the relevant results of the MDC with respect to the control and filtering problems of NSs are very few.

B.Symbolic-Based Encoding-Decoding Mechanism

This kind of encoding schemes,also called as the“binary encoding”,mainly takes the sign of the source into account,and thus only one bit is utilized to encode the signal.For convenience,in the sequel,we call it as the binary encoding instead of the symbolic-based encoding.Usually,the binary encoding technique including two versions,that is,the absolute(static)encoding technique[27],[28]and the differential(dynamic)encoding technique[51],[70].Since the dynamic binary encoding technique is more complicated than the static one,in the following,we will concentrate our attention on the dynamic binary encoding-decoding technique.

As we know,such a kind of dynamic encoding scheme was first proposed in[51],which is highly dependent on the change of certain system parameters.The core of the encoding rule can be expressed as follows with the system model(1)and(3).

where sign(·)is the sign function,g(·)is the decoding function,s(tk)is the codeword generated attk,andis the decoded value of the measurement outputy(tk).It follows from(13)that at each encoding instanttk,only the sign of the change between the two successive measurement outputs is transmitted to the decoder,which implies that only one bit is needed for the codeword delivery during each encoding period.For the decoder design,the expected decoding functiong(·)is generally consisted of two parts,namely,The first term is the decoded value at the last encoding instant and the second one is a compensation function which aims to predict the difference betweeny(tk)andy(tk−1).It is obvious that such an encoding scheme greatly reduces the communication burden and hence becomes a good candidate for the network-based control/ filtering systems subject to communication constraints.On the other hand,since only one-bit information could be obtained at each decoding instant,how to design an effective prediction functiong0(s(tk))so as to ensure the convergence of the decoding error appears to be the main challenge in the design of the encoder-decoder procedure.

III.ENCODING-DECODING-BASED CONTROL AND FILTERING PROBLEMS

In this section,we will go over the recent theoretical developments of both the encoding-decoding-based control and filtering problems from various aspects including controller/ filter design and the system performance evaluation.

A.Encoding-Decoding-Based Stabilization Problems

1)Linear systems:Among the various system performance indices for the networked control systems(NCSs),stability is the most basic yet crucial one,and thus it needs to be first considered in the system design.However,it should be noted that the introduction of the encoding-decoding-based communication scheme inevitably leads to the occurrence of the signal distortion,which would pose considerable additional complexities on the stability analysis and controller synthesis issues.A schematic structure of the NCSs with encodingdecoding-based data transmission protocol can be described in Fig.5.

In[11],the pioneering work has been reported on the NCSs with quantization-based state feedback control strategy,which plays an important role in the subsequent fruitful results on the encoding-decoding schemes.In[134],the stabilization issue for a class of linear time-invariant system subject to the bandwidth constraint has been considered,where the encoding-decoding-based communication protocol has been introduced.For the quantization-based encoding scheme,a sufficient condition for the existence of the bit rate which enables to stabilize the system has been derived.Moreover,when the system reduces to a scalar one,a tight sufficient and necessary condition has been obtained.Nevertheless,the concrete forms of both the encoder and decoder are not explicitly given in their paper.The quadratic stabilization problem for sampled-data systems has been discussed in[42]under a bandwidth-constrained situation,where the memoryless uniform and logarithmic quantizers have been designed to overcome the circumstances of the limited bit rate of the communication channel and an upper bound on the bit rate has been acquired to achieve the stabilization purpose.Furthermore,both the state encoding and output encoding schemes have been developed in[67]for the continuous-time linear systems,and the encoding procedure has been well described in terms of the uniform quantization method.Meanwhile,the quantitative relationship between the number of the values taken from the encoder and the open-loop system parameters has been derived,under which the globally asymptotic stability of the closed-loop system has been guaranteed.Both the detectability and stabilizability problems have been investigated in[111]for the continuous-time systems with Lipschitz nonlinearities and bounded noises.

With the help of “zooming”technique,an observer-based encoding-decoding procedure has been put forward to globally stabilize the closed-loop system without the know ledge of the bound of the initial condition.Motivated by the approach proposed in[111],the subsequent work has been done in a large body of literature.For example,[148]has applied the approach to the discrete-time descriptor systems,and the nonlinearities existing in both the system state and the measurement equations have been considered in[7].Recently,the encoding-scheme-based stabilization issue for the nonlinear uncertain systems has been studied in[66],and the traditional ISS condition has been relaxed to the differentiable ISS one.Moreover,by proposing a new uncertain nonlinear system model,the results obtained in[69]have been further generalized.

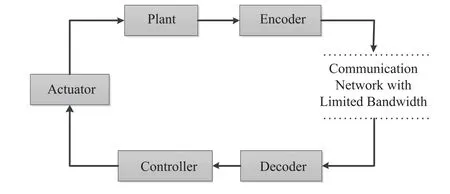
Fig.5.NCSs with the encoding-decoding-based communication protocol.

2)Nonlinear systems:Afterwards,a number of research results have been extended to the encoding-decoding issues for the nonlinear NCSs,see[44],[66],[67],[69],[93],[97]−[99],[111],[148].In[69],by utilizing the decoded system state,a feedback control strategy has been proposed to stabilize a class of continuous-time Lipschitz-type nonlinear systems.The ISS theory has been employed to characterize the impact of the decoding error on the closed-loop system state,based on which,it has been demonstrated that the closed-loop system can achieve globally asymptotical stability as long as the encoding frequency,the amount of the information provided by the encoder and the system parameters satisfy certain inequality conditions.In[98],the integral ISS condition,which is a weaker assumption than the ISS,has been obtained to ensure the stability of the closed-loop system under the same requirement on the channel capacity with[69].Then,[96]extended the result to any smooth nonlinear systems,in which,it has been revealed that if the original nonlinear systems can be stabilized by certain control strategy without encoding process,it can also be stabilized by the state feedback scheme with the designed encoding communication protocol provided the channel capacity is larger than a given lower bound.

B.Encoding-Decoding-Based State Estimation Problems

In order to eliminate the confusion,it should be stated that the state estimation problem considered here is different from the channel state estimation issue[81],[146]which belongs to the scope of information theory and aims to recover the state of the channel to facilitate the information transmission.In the category of control and signal processing,the state estimation(also called filtering)problem is to provide a possible accurate reconstruction of the state of the target plant,and has long been a focus of research due to its engineering insights in many branches,see[36],[38],[41],[55],[62],[63],[79],[80],[82],[83],[115],[116],[124],[131],[144],[145],[149].For the data-rate-constrained NCSs,a typical filter structure with the encoder-decoder pair is shown in Fig.6.In this subsection,an overview will be given on the progress made in the encodingdecoding-based filtering/state estimation problems in the past few years.

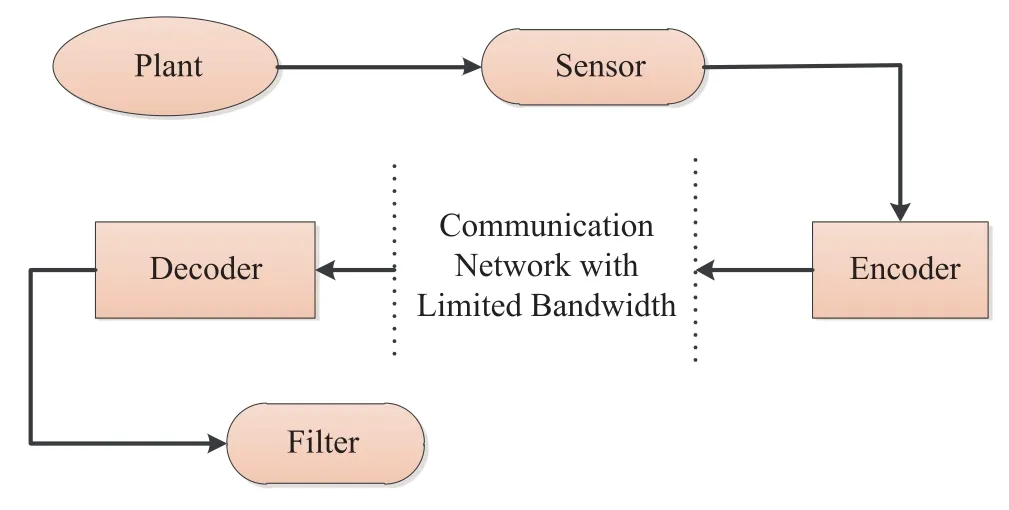
Fig.6.Filtering system model with encoding-decoding-based data transmission scheme.

Some initial attempts devoted to the state estimation problems with the compressed measurement data can be found in[3],[10],and then a rich body of related results have appeared due to the wide utilization of the prevalent network communication techniques in a large range of the practical applications,see[8],[26],[87],[88],[114].For instance,the state estimation problem has been studied in[87]for the linear discrete-time unstable system with a noisy memoryless channel of communication constraints.The estimator has been explicitly designed and an equivalent relationship between estimation performance and the communication capacity of the channel has been revealed.For the same system model,its almost sure observability/stabilizability has been discussed in[88],where the communication channel was noisy and subject to the limited transmission capacity.It has been proved that the capability of the channel to guarantee the almost sure stabilizability/observability of the plant corresponds to its capability to deliver information with zero probability of error.The communication-constrained remote state estimation problem has been addressed in[8],where both the source coding and channel coding have been concerned.Without the assumption of the channel feedback existing in the communication loop,two encoding approaches have been proposed,and then the analysis results on the performance trade-off between the convergence rate of the decoding error and computational complexity have been derived.

It is noted that the results on the encoding-decoding-based state estimation problems recalled above are generally based on the information theoretic aspects,while,in recent years,there also has a surge of research attention on this issue from the point of non-information-theoretic view,see[34],[86],[92],[117],[138],[139].In[86],the robust set-valued state estimation problem has been addressed for the continuous-time uncertain systems via a digital communication with limited bit rate,where two encoding-decoding-based state estimation schemes have been presented from the aspects of the estimation precision and the algorithm implementation,respectively.The concept of “maxim in information functional”has been established in[92]under a nonstochastic information theory framework,by which,it has been verified that the largest maximin information rate through a memoryless and errorprone channel reflects the zero-error capacity of the channel and the result has been applied to the state estimation issue for a linear time-invariant system.By applying the linear temporal coding technique,the optimal state estimation problem has been investigated in[34]for a class of discrete-time system with an unreliable channel.Both the orthogonal projection principle and the innovation sequence method have been employed to derive the minimum mean square estimation algorithm.The extended work has been done in[117],where the state estimation problem for the linear discrete-time stochastic systems subject to the packet dropout has been considered.In order to compensate the negative effect of the packet loss on the estimation performance,a linear coding temporal scheme has been employed to the raw measurements,by which some necessary and sufficient conditions for the estimation error system have been established in the mean square sense.

C.Encoding-Decoding-Based Control/State Estimation Subject to Network-Enhanced Complexities

In the remote networked control/estimation systems,because of the power restriction,network congestion or error,it is unavoidable that the data transmission via the digital channel suffers from the communication imperfections,e.g.,transmission delay,message loss,channel noise,etc.In this sense,for the encoding-decoding-based control/ filtering problem in NCSs,the inherent complexities of the analysis and design issues have been typically enhanced and a number of relevant results have been reported in[19],[21],[31],[43],[45],[77],[100],[123],[129],[132].

1)Time-delays:In[100],the minimal data-rate stabilization problem has been solved for the nonlinear NSs with transmission delays,which can be arbitrarily large.By applying the tool of the hybrid system theory,the original system has been converted into a couple of impulsive delayed nonlinear systems,and the semi-global and local stability of the closedsystem has been guaranteed.The stabilization problem has been concerned in[21]for a class of distributed linear systems by a remote centralized control scheme,in which the random packet dropout and communication delay caused by an erasure network have been simultaneously considered.Three scenarios of the availability of the feedback channel have been,respectively,discussed and different encoding strategies have been correspondingly provided to ensure the closed-loop stability in the mean absolute sense.In[31],the channel coding technique has been adopted to reduce the occurrence of packet dropouts for the NCSs.However,the redundancy of the channel coding would lead to the time-delays.In order to balance such a tradeoff,the ON-OFF channel coding technique has been utilized where the coding operation was adaptively implemented according to the expectation value of the tracking error.The datarate-constrained stabilization problem has been investigated in[123]for a class of continuous-time linear system.Due to the limited communication capacity of the channel between the sensor and controller,the sampled data has been encoded to certain codewords by the spherical polar coordinates encoding scheme.Dependent on whether the control inputs were needed to be sent to the decoder,two coding methods have been developed to achieve the stability of the controlled system.

2)Packet-dropouts:For the random ly occurring message loss during the data transmission,a subband coding technique has been employed in[43]to deal with the controller and encoder-decoder pair design issues.To facilitate the analysis of the encoding-decoding procedure,the addressed control problem has been tackled in the frequency domain,and the stochastic stability and the H∞performance have been ensured in terms of the solution to certain linear matrix inequalities(LM Is).In[45],the attention has been focused on the stabilization problem for the discrete-time linear NCSs,where the data transmission has been implemented via a lossy channel with finite data rate.For the aim of the data compression,the control signal has been encoded to finite values by the uniform quantization method and a buffer has been designed in order to compensate the packet-dropout effect.

For the sake of improving the data transmission reliability via the erasure channel and obtaining a relatively satisfactory control/estimation performance,the multiple description encoding technique has been adopted in the NCSs in recent years.The MD encoding approach has been first introduced in the NCSs in[47],in which the Kalman filtering problem has been investigated for linear stochastic systems.Due to the packet dropout existing in the data packet transmission via the communication network,the MD encoding scheme has counteracted the effects of the data loss on the filtering performance.It has been demonstrated that compared with the single description encoding scheme,the MD one could significantly enhance the filtering performance.In[94],the state estimation problem has been addressed in the sensor networks together with the power control mechanism.The sensors were required to transmit the measurements to the gateway via a lossy channel subject to random packet dropouts,and then a novel MD quantizer has been applied to improve the estimation robustness.For more details with respect to the encodingdecoding-based filtering issues with lossy/noisy channels,we refer the readers to[72],[95],[103],[118]and the references therein.

3)Event-triggering mechanism:It is recognized that the signal delivery through the communication channel,especially for the wireless network,would account for a major ratio in the total power consumption of the NCSs.Therefore,for the purpose of keeping the use of the energy resource as small as possible and alleviating the network collision,the eventtriggering data transmission mechanism has been successfully applied in the NCSs of digital communications[40],[58],[61],[70],[75],[78],[119],[128].In[52],the early attempt has been made on the combination of the quantization-based control approach and the event-triggering approach to address the stabilization problem for linear continuous-time systems.Based on the quantization method utilized in[67],an encoderdecoder pair has been proposed to reduce the amount of the information to be sent via a bit-data-constrained channel,meanwhile,the event-triggered scheme has been employed to decrease the communication frequency.The boundedness of the closed-loop system state and a lower upper of the minimum time interval between two successive events have been explicitly studied.Very recently,for a linear scalar system with the communication delay,an event-triggered control problem combining with the quantization-based encodingdecoding scheme has been investigated in[49].The additional information of the event-triggering time has been further excavated,and it has been shown that for the sufficiently small time delay,the timing information carried by the triggered events is large enough to stabilize the closed-loop system with any small information transmission rate.Subsequently,the related work has been extended to the vector systems in[50]and the binary differential coding approach in[70].

D.Optimal Encoding-Decoding Schemes

In the context of bit-rate-constrained control/estimation problems,the optimal coding scheme can be described from two aspects:1)deriving the optimal control/ filtering performance with a fixed bit rate of the network,and 2)determining the minimum information needed to transmit in order to achieve a given control/ filtering task.

1)Optimal control/estimation performance:In the first sense,there has been attracting considerable attention in recent years,see e.g.[1],[12],[25],[27],[46],[110],[130],[147].In[110],the optimal control problem for discrete-time nonlinear uncertain systems via digital communication channels with limited capacity has been taken into account.Based on the introduced concept“topological entropy”,sufficient and necessary conditions,which are related to the bit rate of the channel and the topological entropy of the open-loop system,have been established for the solvability of the addressed optimal control problem.In[1],the control problem for a class of nonlinear systems subject to the communication constraints has been investigated.A performance index characterizing the difference between the quantized and unquantized systems has been defined.By optimizing such an index,the optimal dynamic quantizer in a closed form has been obtained.[147]has considered the distributed estimation issue through a sensor network with the limited transmission capacity,in which an optimal-quantization-based encoding-decoding algorithm has been put forward to minimize the estimation error.The tracking problem has been addressed in[25]via a signalnoise-ratio-constrained communication network.Two practical network architectures have been illustrated to model the transmission channel.Moreover,the optimal encoder-decoder pair has been found,by which the tracking error variance has been minimized with minimum information transmissions.

2)Minimum data-rate:During the past fifteen years,the minimum data-rate problem has gained a great deal of research attention in the network-based control and signal processing areas,see e.g.[35],[90],[91],[104],[109],[120].Some initial effort has been made in[90],in which the stabilization problem has been considered for the linear discretetime systems with the limited communication capacity.By resorting to the asymptotic quantization theory,a sufficient and necessary condition has been obtained for the existence of the minimum lower bound of the bit rate,above which the closedloop system can be stabilized in the m th moment sense.The exponential stabilization problem with limited feedback data rates has been studied in[91],and moreover,the minimum data rate has been given which can achieve the system stability.In[35],the minimum bit rate has been obtained to stabilize the linear time-invariant systems for both the continuoustime and the discrete-time cases.By applying the differential pulse code modulation techniques,the comparison results have been provided with respect to the derived minimum bit rate for the fix-step quantization and the variable-step quantization approaches.Very recently,a joint optimization problem has been discussed in[104].For a NCS with the ratelimited communication channel,a general performance index including both the control cost and the communication cost has been constructed,and the corresponding optimal control and encoding problem has been solved.

IV.DISTRIBUTED CONTROL AND STATE ESTIMATION PROBLEMSW ITH LIM ITED COMMUNICATION CAPACITY

Compared with the simple NCS which only consists of the single plant and controller/estimator,the distributed networked systems are more widespread in the real-world,such as the chemical process systems,the biological systems,the unmanned aerial vehicles,etc.For those large-scale distributed systems,each individual can be viewed as an agent which has the capacity of sensing,communication,computation,and implementation.In practical applications,the MASs and the WSNs are two typical examples of the distributed systems,and the corresponding distributed control and state estimation problems have attracted increasing research attention in recent years.Since the frequent information exchange among agents would certainly occupy considerable network resource and power energy,the effective data-compression and energysaving transmission mechanisms are vitally meaningful in real engineering systems.The typical framework of the distributed networked system with encoding-decoding communication is given by Fig.7.In this section,we aim to provide some recent developments with respect to the encoding-decodingbased distributed control problem for the MASs and the state estimation problem for the WSNs,respectively.

Fig.7.The architecture of distributed systems with encoding-decoding communication mechanism.

A.Multi-Agent Systems With Encoding-Decoding-Based Information Transmission

1)Without network-induced phenomena:Consensus is one of the most important collective behaviors for the MASs,and the related control problems have received remarkable research interests in the past decade,see e.g.[32],[74],[85],[135],[140],[142].It is known from[64]that the encodingdecoding-based consensus control protocol for MASs was first proposed in[5],in which,the average consensus performance has been investigated for a class of linear MASs by the bit-rate-constrained control protocol.According to different quantization strategies,two encoding-decoding schemes have been provided which would guarantee the desired average consensus if the communication network is strongly connected.Under a connected communication network with limited data transmission capacity,[56]has explored the average consensus control problem for the first-order linear discrete-time MASs.By designing a dynamic encoding-decoding-based distributed control law,the exponential average consensus has been ensured for the requirement that only one bit data exchanged between two adjacent agents.Furthermore,an energy index has been defined to characterize the communication energy consumption for the consensus task,by optimizing which,a trade-off between the consensus rate and the quantization levels has been presented.Then,[64]has extended to the time-varying topologies case which is of jointly connected and the quantized observer-based encoding-decoding consensus control problem has been considered in[65]for the secondorder discrete-time MASs.The related results with respect to high-order MASs can be found in[101].

2)Subject to network-induced complexities:In the above results,a common assumption is that the communication channel is noiseless,i.e.,no time-delays,dropouts,external disturbances,etc.during the data transmission process.However,this is not always true in the engineering practical owing to the limited network resources and the environmental complexity.In[73],the authors have discussed the average consensus problem of the MASs subject to bit-rate constraint,where the communication delays have been taken into consideration.By means of constructing a pair of dynamic encoder and decoder,a consensus control protocol has been designed to reach the average consensus performance with bounded time-delays.Because of the merits in the reduction of the energy and network resource,the event-triggering transmission mechanism has recently been adopted in the distributed control problem of the MASs with bandwidth restrictions,see e.g.[6],[29],[54],[141].In[54],in order to handle the consensus control problem for a class of discrete-time MASs via an imperfection communication network,both the eventtriggering transmission mechanism and the dynamic encodingdecoding scheme have been employed.The proposed encoding scheme could adaptively select the number of the channel quantization level at each time step,and the relationship among the convergence rate,the number of the agents,the quantization interval,the network structure,and control gain has been well illustrated.Based on[54],very recently,the distributed consensus optimization problem for the MASs has been put forward in[57].For each agent,a convex cost function has been defined and the objective optimization function was the sum of those individual cost functions.It also has been proved that as long as the system parameters satisfy certain conditions,the optimality of the consensus control scheme can be guaranteed with only one bit information exchange for each pair of adjacent agents.The similar problem with some extensions has been investigated in[59].

B.Wireless Sensor Networks With Encoding-Decoding-Based Communication Scheme

A wireless sensor network(WSN)is usually composed of numerous simple and low-cost sensor nodes geographically deployed in certain areas.With the collaboration such as the integrated sensing,computation and communication,those sensor nodes can jointly perform various tasks in wide application fields including environmental monitoring,battle field surveillance,civil infrastructure monitoring and control,intelligent solar farms,etc.,[13],[14],[16],[17],[33],[60],[84],[125],[127],[132].However,it should be stressed that due to the frequent communications among sensor nodes powered by irreplaceable batteries,the scarce network bandwidth and energy resources would give rise to a severe limitation on the practical applications of the WSNs.Therefore,developing certain useful communication techniques,which aims to improve the efficiency of the bandwidth utilization and reduce the energy consumption,appears to be an urgent task.

So far,an alternative way to facilitate the information exchange in a bit-rate-constrained WSN is to design appropriate data encoding-decoding schemes so as to reduce the number of transmitted bits at each data transmission process,see[22],[107],[108].In[108],the distributed filtering problem has been considered for a class of continuous-time stochastic systems with a low communication capacity.For each sensor,the observation value is required to be encoded into one bit information to be transmitted,based on which,a recursive algorithm of the Kalman filtering type has been designed.Also,it has been revealed that encoding-decodingbased filtering algorithm can achieve a close performance with the standard Kalman filtering algorithm.The distributed parameter estimation issue via the bandwidth-restricted WNSs has been studied in[20],in which the distributed adaptive quantization approach and a sequential transmission strategy have been employed.Based on the adaptive quantization approach,three quantization schemes have been proposed and the corresponding maximum likelihood estimators have been designed.

By using the observations from multiple sensors,[53]has researched the distributed state estimation problem for a discrete-time linear system.Because of the data-rate constraint,the individual sensors’innovations are required to be quantized before sending to the fusion center.The stability of the estimation scheme can be achieved if the data-rate for each sensor is sufficiently large.In addition,an optimal rate allocation issue for the individual sensors has been discussed.[89]has studied the distributed parameter estimation problem in an energy-constrained WSN,where only one bit for each sensor has been allowed to be sent to the fusion center.On the basis of the variance of the measurement noises of individual sensors,the mean square estimation error can be minimized by designing an optimal bit assignment scheme.In[105],based on the Kalman filter structure,a distributed state estimation problem has been dealt with for the microgrid,and the systematic convolution encoding approach has been developed to facilitate the smart grid communications.By applying the energy measurements from the bit-rate-constrained sensor networks,the target location estimation problem has been addressed in[71].A position-based adaptive quantization scheme has been provided to improve the estimation performance,and the maximum likelihood estimator and the corresponding Cramér–Rao lower bound have been obtained.In[102],the distributed state estimation issue has been handled via a lossy WSN.By using the encoded measurements,the Kalman filter has been constructed to estimate the system state at the gateway,which also has controlled the transmission power of the radio power amplifier and the bit rate needed for each sensor.

V.CONCLUSIONS AND FUTUREWORK

Throughout this paper,we have summarized the existing results on the encoding-decoding-based control and state estimation/ filtering issues for NSs.Several typical encoding-decoding schemes and the corresponding encoder-decoder structures have been systematically reviewed.Subsequently,for different kinds of NSs,a variety of encoding-decoding-based control and state estimation problems have been thoroughly surveyed.Finally,based on the literature review,possible relative directions for the further research work are listed as follows.

1)Channel encoding.So far,most of the existing results focus their attention on the aspect of source encoding and decoding.In fact,the channel encoding-decoding is also very important for the reliability of the data transmission in the communication network.Therefore,it is quite meaningful to study the co-design issue of the source and channel encodingdecoding in NSs.

2)Combining with other communication protocols.Recently,some effective data scheduling strategies such as the Round-Robin protocol,the Try-Once-Discard protocol,the stochastic protocol,etc.,have been successfully applied to the NSs in order to cope with the limited communication resources.For the purpose of making full use of the network resources,the development of several encoding-decodingbased data scheduling protocols would be a trend for future research.

3)Data encryption issues.Since NSs share the common network links for data exchange,they are prone to be attacked by adversaries,and the secure communication in NSs becomes more and more significant.Thereby,how to combine the encoding-decoding schemes with the data encryption techniques in a unified framework is another interesting topic.

4)Combining with self-triggering mechanism.Although there have been some results with respect to the combination of the event-triggering mechanism and the decoding-decoding communication schemes recently,the additional hardware is still needed to detect the specific “event”.In this sense,by replacing the detection task according to certain admissible “prediction”[150],the self-triggering mechanism is one preferable candidate to facilitate the encoding-decoding-based control/ filtering problems.

[1]S.Azuma and T.Sugie,“Dynamic quantization of nonlinear control systems,”IEEE Transactions on Automatic Control,vol.57,no.4,pp.875-888,Apr.2012.

[2]H.Bai,M.Zhang,A.Wang,M.Liu,and Y.Zhao,“Multiple description video coding using inter-and intra-description correlation at macro block level,”IEICE Transactions on Information and Systems,vol.E97D,no.2,pp.384-387,Feb.2014.

[3]Y.Barshalom,“Redundancy and data compression in recursive estimation,”IEEE Transactions on Automatic Control,vol.AC17,no.5,pp.684-689,1972.

[4]Y.Berrouche and R.E.Bekka,“Improved multiple description wavelet based image coding using Hadamard transform,”AEU-International Journal of Electronics and Communications,vol.68,no.10,pp.976-982,2014.

[5]R.Carli,F.Fagnani,and P.Frasca,“Efficient quantized techniques for consensus algorithms,”NeCST workshop,pp.1-8,Nancy,France,2007.

[6]X.Chen,X.Liao,L.Gao,S.Yang,H.Wang,and H.Li,“Eventtriggered consensus for multi-agent networks with switching topology under quantized communication,”Neurocomputing,vol.230,pp.294-301,Mar.2017.

[7]T.M.Cheng,“Robust output feedback stabilization of nonlinear networked systems via a finite data-rate communication channel,”Journal of Systems Science&Complexity,vol.24,no.1,pp.1-13,Feb.2011.

[8]G.Como,F.Fagnani,and S.Zampieri,“Anytime reliable transmission of real-valued information through digital noisy channels,”SIAM Journal on Control and Optimization,vol.48,no.6,pp.3903-3924,2010.

[9]P.Correia,P.A.Assuncao,and V.Silva,“Multiple description of coded video for path diversity streaming adaptation,”IEEE Transactions on Multimedia,vol.14,no.3,pp.923-935,Jun.2012.

[10]C.E.Curry,P.Mirchandani,and C.F.Price,“State estimation with coarsely quantized,high data-rate measurements,”IEEE Transactions on Aerospace and Electronic Systems,vol.11,no.4,pp.613-621,1975.

[11]D.F.Delchamps,“Stabilizing a linear-system with quantized state feedback,”IEEE Transactions on Automatic Control,vol.35,no.8,pp.916-924,Aug.1990.

[12]S.Dey,A.Chiuso,and L.Schenato,“Event-triggered stabilization of linear systems under bounded bit rates,”IEEE Transactions on Automatic Control,vol.62,no.6,pp.3054-3061,Jun.2017.

[13]D.Ding,Z.Wang,D.W.C.Ho,and G.Wei,“Distributed recursive filtering for stochastic systems under uniform quantizations and deception attacks through sensor networks,”Automatica,vol.78,pp.231-240,Feb.2017.

[14]D.Ding,Z.Wang,B.Shen,and H.Dong,“Event-triggered distributedH∞state estimation with packet dropouts through sensor networks,”IET Control Theory&Applications,vol.9,no.13,pp.1948-1955,Aug.2015.

[15]D.Ding,G.Wei,S.Zhang,Y.Liu,and F.E.Alsaadi,“On scheduling of deception attacks for discrete-time networked systems equipped with attack detectors,”Neurocomputing,vol.219,pp.99-106,Jan.2017.

[16]H.Dong,X.Bu,N.Hou,Y.Liu,F.E.A lsaadi,and T.Hayat,“Eventtriggered distributed state estimation for a class of time-varying systems over sensor networks with redundant channels,”Information Fusion,vol.36,pp.243-250,Jul.2017.

[17]H.Dong,Z.Wang,J.Lam,and H.Gao,“Distributed filtering in sensor networks with randomly occurring saturations and successive packet dropouts,”International Journal of Robust and Nonlinear Control,vol.24,pp.1743-1759,Aug.2014.

[18]A.A.Elgamal,T.M.Cover,“Achievable rates for multiple descriptions,”IEEE Transactions on Information Theory,vol.28,no.6,pp.851-857,Aug.1982.

[19]J.Fang and Q.-Q.Liu,“Quantized feedback control over packet dropout communication channels,”Information Technology and Control,vol.41,no.3,pp.229-238,2012.

[20]J.Fang and H.Li,“Distributed adaptive quantization for wireless sensor networks:From delta modulation to maximum likelihood,”IEEE Transactions on Signal Processing,vol.56,no.10,pp.5246-5257,Oct.2008.

[21]A.Farhadi,“Feedback channel in linear noiseless dynamic systems controlled over the packet erasure network,”International Journal of Control,vol.88,no.8,pp.1490-1503,Aug.2015.

[22]A.Farhadi and N.U.Ahmed,“Tracking nonlinear noisy dynamic systems over noisy communication channels,”IEEE Transactions on Communications,vol.59,no.4,pp.955-961,Apr.2011.

[23]A.Farhadi and C.D.Charalambous,“Robust coding for a class of sources:Applications in control and reliable communication over limited capacity channels,Systems&Control Letters,”vol.57,no.12,pp.1005-1012,Dec.2008.

[24]A.Farhadi and C.D.Charalambous,“Stability and reliable data reconstruction of uncertain dynamic systems over finite capacity channels,Automatica,”vol.46,no.5,pp.889-896,May 2010.

[25]Y.W.Feng and G.Ge,“Optimal coding-decoding for systems controlled via a communication channel,”International Journal of Systems Science,vol.44,no.12,pp.2190-2198,Dec.2013.

[26]A.L.Fradkov,B.Andrievsky,and M.Ananyevskiy,“State estimation and synchronization of pendula systems over digital communication channels,”European Physical Journal-Special Topics,vol.223,no.4,pp.773-793,Apr.2014.

[27]A.L.Fradkov,B.Andrievsky,and R.J.Evans,“Chaotic observerbased synchronization under information constraints,Physical Review E,”vol.73,no.6,Article Number:066209,Jun.2006.

[28]A.L.Fradkov,B.Andrievsky,and R.J.Evans,“Synchronization of passifiable Lurie systems via limited-capacity communication channel,”IEEE Transactions on Circuits And Systems I-Regular Papers,vol.56,no.2,pp.430-439,Feb.2009.

[29]L.Gao,X.Liao,H.Li,and G.Chen,“Event-triggered control for multi-agent network with limited digital communication,Nonlinear Dynamics,”vol.82,no.4,pp.1659-1669,Dec.2015.

[30]V.K.Goyal,“Multiple description coding:Compression meets the network,IEEE Transactions on Signal Processing Magazine,”vol.18,no.5,pp.74-93,Sept.2001.

[31]S.Hattori,K.Kobayashi,H.Okada,and M.Katayama,“On-off error control coding scheme for minimizing tracking error in wireless feedback,”IEEE Transactions on Industrial Informatics,vol.11,no.6,pp.1411-1421,Dec.2015.

[32]F.Han,G.Wei,D.Ding,and Y.Song,“Finite-horizonH∞-consensus control for multi-agent systems with random parameters:The local condition case,”Journal of The Franklin Institute-Engineering and Applied Mathematics,vol.354,no.14,pp.6078-6097,Sept.2017.

[33]F.Han,G.Wei,D.Ding,and Y.Song,“Local condition based consensus filtering with stochastic nonlinearities and multiple missing measurements,”IEEE Transactions on Automatic Control,vol.62,no.9,pp.4784-4790,Sept.2017.

[34]L.He,D.Han,X.Wang,and L.Shi,“State estimation over a lossy network using linear temporal coding,inProceedings of the 51st IEEE Conference on Decision and Control,”pp.2002-2007,Maui,Hawaii,USA,Dec.2012.

[35]J.Hespanha,A.Ortega,and L.Vasudevan,“Towards the control of linear systems with minimum bit-rate,inProceedings of the 15th International Symposium on Mathematical Theory of Networks and Systems,”pp.1-15,Notre Dame,Indiana,USA,Aug.2002.

[36]N.Hou,H.Dong,Z.Wang,W.Ren,and F.E.Alsaadi,“Non-fragile state estimation for discrete Markovian jumping neural networks,”Neurocomputing,vol.179,pp.238-245,Feb.2016.

[37]N.Hou,H.Dong,Z.Wang,W.Ren,and F.E.Alsaadi,“H∞state estimation for discrete-time neural networks with distributed delays and random ly occurring uncertainties through fading channels,”Neural Networks,vol.89,pp.61-73,May 2017.

[38]J.Hu,Z.Wang,and H.Gao,“Recursive filtering with random parameter matrices,multiple fading measurements and correlated noises,”Automatica,vol.49,no.11,pp.3440-3448,Nov.2013.

[39]L.Hu,Z.Wang,Q.-L.Han,and X.Liu,“State estimation under false data injection attacks:Security analysis and system protection,”Automatica,vol.219,pp.176-183,2018.

[40]L.Hu,Z.Wang,Q.-L.Han,and X.Liu,“Event-based input and state estimation for linear discrete time-varying systems,”International Journal of Control,in press.DOI:10.1080/00207179.2016.1269205.

[41]J.Hu,Z.Wang,S.Liu,and H.Gao,“A variance-constrained approach to recursive state estimation for time-varying complex networks with missing measurements,”Automatica,vol.64,pp.155-162,Feb.2016.

[42]H.Ishii,B.A.Francis,“Quadratic stabilization of sampled-data systems with quantization,”Automatica,vol.39,no.10,pp.1793-1800,Oct.2013.

[43]H.Ishii,S.Hara,“A subband coding approach to control under limited data rates and message losses,”Automatica,vol.44,no.4,pp.1141-1148,Apr.2008.

[44]A.Isidori,L.Marconi,C.de Persis,“Remote tracking via encoded information for nonlinear systems,”Systems&Control Letters,vol.55,no.10,pp.809-818,Oct.2006.

[45]Y.Isidori,K.Takaba,and D.E.Quevedo,“Stability analysis of networked control systems subject to packet-dropouts and finite-level quantization,”Systems&Control Letters,vol.60,no.5,pp.325-332,May 2011.

[46]X.-W.Jiang,B.Hu,Z.-H.Guan,X.-H.Zhang,and L.Yu,“Best achievable tracking performance for networked control systems with encoderdecoder,”Information Sciences,vol.305,pp.184-195,Jun.2015.

[47]Z.Jin,V.Gupta,and R.M.Murray,“State estimation over packet dropping networks using multiple description coding,”Automatica,vol.42,no.9,pp.1141-1152,Sept.2006.

[48]D.Kapetanovic,S.Chatzinotas,and B.Ottersten,“Index assignment for multiple description repair in distributed storage systems,”inProceedings of the 2014 IEEE International Conference on Communications,pp.3896-3901,Sydney,Australia,Jun.10-14,2014.

[49]M.J.Khojasteh,P.Tallapragada,J.Cortes,and M.Franceschetti,“The value of timing information in event-triggered control:The scalar case,”inProceedings of the 54th Annual Allerton Conference on Communication,Control,and Computing,pp.1165-1172,Monticello,USA,Sept.27-30,2016.

[50]M.J.Khojasteh,P.Tallapragada,J.Cortes,and M.Franceschetti,“Time-triggering versus event-triggering control over communication channels,”inarXiv:1703.10744[math.OC].

[51]E.Kofman and J.H.Braslavsky,“Level crossing sampling in feedback stabilization under data-rate constraints,”inProceedings of the 45th IEEE Conference on Decision and Control,pp.4423-4428,San Diego,California,USA,Dec.2006.

[52]D.Lehmann and J.Lunze,“Event-based control using quantized state information,”inProceedings of the 2nd IFAC Workshop on Distributed Estimation and Control in Networked Systems,pp.1989-1994,Annecy,France,2010.

[53]A.S.Leong,D.Subhrakanti,and G.N.Nair,“Quantized filtering schemes for multi-sensor linear state estimation:stability and performance under high rate quantization,”IEEE Transactions on Signal Processing,vol.61,no.15,pp.3852-3865,Aug.2013.

[54]H.Li,G.Chen,T.Huang,Z.Dong,and L.Gao,“Event-triggered distributed average consensus over directed digital networks with limited communication bandwidth,”IEEE Transactions on Cybernetics,vol.46,no.12,pp.3098-3110,Dec.2016.

[55]J.Li,H.Dong,F.Han,N.Hou,and X.Li,“Filter design,fault estimation and reliable control for networked time-varying systems:A survey,”Systems Science&Control Engineering:An Open Access Journal,vol.5,pp.331-341,2017.

[56]T.Li,M.Fu,L.Xie,and J.Zhang,“Distributed consensus with limited communication data rate,”IEEE Transactions on Automatic Control,vol.56,no.2,pp.279-292,Feb.2011.

[57]H.Li,C.Huang,G.Chen,X.Liao,and T.Huang,“Distributed consensus optimization in multiagent networks with time-varying directed topologies and quantized communication,”IEEE Transactions on Cybernetics,vol.47,no.8,pp.2044-2057,Aug.2017.

[58]L.Li,M.Lemmon,and X.Wang,“Stabilizing bit-rates in quantized event triggered control systems,”inProceedings of The 15th ACM International Conference on Hybrid Systems:Computation and Control,pp.245-254,Beijing,P.R.China,2012.

[59]H.Li,S.Liu,Y.C.Soh,and L.Xie,“Event-triggered communication and data rate constraint for distributed optimization of multiagent systems,”IEEE Transactions on Systems,Man,and Cybernetics:Systems,in press.DOI:10.1109/TSMC.2017.2694323.

[60]Q.Li,B.Shen,Z.Wang,and F.E.Alsaadi,“A sampled-data approach to distributedH∞resilient state estimation for a class of nonlinear time-delay systems over sensor networks,”Journal of the Franklin Institute,vol.354,pp.7139-7157,Oct.2017.

[61]L.Li,X.Wang,M.D.Lemmon,“Efficiently attentive event-triggered systems with limited bandwidth,”IEEE Transactions on Automatic Control,vol.62,no.3,pp.1491-1497,Mar.2017.

[62]W.Li,G.Wei,D.Ding,Y.Liu,and F.E.Alsaadi,“A new look at boundedness of error covariance of kalman filtering,”IEEE Transactions on Systems,Man,and Cybernetics:Systems,in press.DOI:10.1109/TSMC.2016.2598845.

[63]W.Li,G.Wei,F.Han,and Y.Liu,“Weighted average consensusbased unscented Kalman filtering,”IEEE Transactions on Cybernetics,vol.46,no.2,pp.558-567,Feb.2016.

[64]T.Li and L.Xie,“Distributed consensus over digital networks with limited bandwidth and time-varying topologies,”Automatica,vol.47,no.9,pp.2006-2015,Sept.2011.

[65]T.Li and L.Xie,“Distributed coordination of multi-agent systems with quantized-observer based encoding-decoding,”IEEE Transactions on Automatic Control,vol.57,no.12,pp.3023-3037,Dec.2012.

[66]X.Li,C.Li,and M.Z.Q.Chen,“Stabilisation of non-linear DISS systems with uncertainty via encoded feedback,”IET Control Theory&Applications,vol.11,no.5,pp.732-739,Mar.2017.

[67]D.Liberzon,“On stabilization of linear systems with limited information,”IEEE Transactions on Automatic Control,vol.48,no.2,pp.304-307,Feb.2003.

[68]D.Liberzon,“Hybrid feedback stabilization of systems with quantized signals,”Automatica,vol.39,no.3,pp.1543-1554,Sept.2003.

[69]D.Liberzon,J.P.Hespanha,“Stabilization of nonlinear systems with limited information feedback,”IEEE Transactions on Automatic Control,vol.50,no.6,pp.910-915,Jun.2005.

[70]Q.Ling,“Bit rate conditions to stabilize a continuous-time scalar linear system based on event triggering,”IEEE Transactions on Automatic Control,vol.62,no.8,pp.4093-4100,Aug.2017.

[71]G.Liu,H.Liu,H.Chen,C.Zhou,and L.Shu,“Position-based adaptive quantization for target location estimation in wireless sensor networks using one-bit data,”Wireless Communications&Mobile Computing,vol.16,no.8,pp.929-941,Jun.2016.

[72]Q.Liu and J.Fan,“State estimation for networked control systems using fixed data rates,”International Journal of Systems Science,vol.48,no.9,pp.1818-1828,2017.

[73]S.Liu,T.Li,and L.Xie,“Distributed consensus for multiagent systems with communication delays and limited data rate,”SIAM Journal on Control and Optimization,vol.49,no.6,pp.2239-2262,2011.

[74]S.Liu,T.Li,L.Xie,M.Fu,and J.Zhang,“Continuous-time and sampled-data-based average consensus with logarithmic quantizers,”Automatica,vol.49,no.11,pp.3329-3336,Nov.2013.

[75]S.Liu,Y.Song,D.Ding,and Y.Liu,“Event-triggered dynamic output feedback RMPC for polytopic systems with redundant channels:Inputto-state stability,”Journal of the Franklin Institute-Engineering and Applied Mathematics,vol.354,no.7,pp.2871-2892,May 2017.

[76]S.Liu,Y.Song,G.Wei,and X.Huang,“RMPC-based security problem for polytopic uncertain system subject to deception attacks and persistent disturbances,”IET Control Theory&Applications,vol.11,no.10,pp.1611-1618,Jun.2017.

[77]W.Liu,Z.Wang,and N.M ingkang,“Controlled synchronization for chaotic systems via limited information with data packet dropout,”Automatica,vol.49,no.11,pp.3329-3336,Nov.2013.

[78]H.Liu,Z.Wang,B.Shen,and X.Liu, “Event-triggeredH∞state estimation for delayed stochastic memristive neural networks with m issing measurements:The discrete time case,”IEEE Transactions on Neural Networks and Learning Systems,in press.DOI:10.1109/TNNLS.2017.2728639.

[79]H.Liu,Z.Wang,B.Shen,and F.E.Alsaadi,“H∞state estimation for discrete-time mem ristive recurrent neural networks with stochastic time-delays,”International Journal of General Systems,vol.45,no.5,pp.633-647,2016.

[80]S.Liu,G.Wei,Y.Song,and Y.Liu,“Extended Kalman filtering for stochastic nonlinear systems with random ly occurring cyber attacks,”Neurocomputing,vol.207,pp.708-716,Sept.2016.

[81]M.B.Loiola,R.R.Lopes,and J.M.T.Romano,“Modified Kalman filters for channel estimation in orthogonal space-time coded systems,”IEEE Transactions on Automatic Control,vol.60,no.1,pp.533-538,Jan.2012.

[82]Y.Luo,Z.Wang,G.Wei,and F.E.Alsaadi,“RobustH∞filtering for a class of two-dimensional uncertain fuzzy systems with randomly occurring mixed delays,”IEEE Transactions on Fuzzy Systems,vol.25,no.1,pp.70-83,Feb.2017.

[83]Y.Luo,Z.Wang,G.Wei,F.E.Alsaadi,and T.Hayat,“State estimation for a class of artificial neural networks with stochastically corrupted measurements under Round-Robin protocol,”Neural Networks,vol.77,pp.70-79,May 2016.

[84]L.Ma,Z.Wang,Q.-L.Han,and H.K.Lam,“Variance-constrained distributed filtering for time-varying systems with multiplicative noises and deception attacks over sensor networks,”IEEE Sensors Journal,vol.17,no.7,pp.2279-2288,Apr.2017.

[85]L.Ma,Z.Wang,and H.K.Lam,“Event-triggered mean-square consensus control for time-varying stochastic multi-agent system with sensor saturations,”IEEE Transactions on Automatic Control,vol.62,no.7,pp.3524-3531,Jun.2017.

[86]V.Malyavej and A.V.Savkin,“Set-valued robust Kalman state estimation via digital communication channels with bit-rate constraints,”inProceedings of the American Control Conference Denver,Colorado,USA,Jun.4-6,2003.

[87]A.S.Matveev,“State estimation via limited capacity noisy communication channels,”Mathematics of Control Signals and Systems,vol.20,no.1,pp.1-35,Mar.2008.

[88]A.S.Matveev and A.V.Savkin,“Shannon zero error capacity in the problems of state estimation and stabilization via noisy communication channels,”International Journal of Control,vol.80,no.2,pp.241-255,Feb.2007.

[89]S.Movaghati and M.Ardakani,“Optimum bit-sensor assignment for distributed estimation in inhomogeneous sensor networks,”IEEE Communications Letters,vol.18,no.4,pp.668-671,Apr.2014.

[90]G.N.Nair and R.J.Evans,“Stabilization with data-rate-limited feedback:tightest attainable bounds,”Systems&Control Letters,vol.41,no.1,pp.49-56,Sept.2000.

[91]G.N.Nair and R.J.Evans,“Exponential stabilisability of finitedimensional linear systems with limited data rates,”Automatica,vol.39,no.4,pp.585-593,Apr.2003.

[92]G.N.Nair,“A nonstochastic information theory for communication and state estimation,”IEEE Transactions on Automatic Control,vol.58,no.6,pp.1479-1510,Jun.2013.

[93]D.Nešić and D.S.Laila,“A note on input-to-state stabilization for nonlinear sampled-data systems,”IEEE Transactions on Automatic Control,vol.47,no.7,pp.1153-1158,Jul.2002.

[94]J.Ostergaard,D.E.Quevedo,and A.Ahlen,“Predictive power control and multiple-description coding for wireless sensor networks,”inProceedings of the IEEE International Conference on Acoustics,Speech,and Signal Processing,Taipei,Taiwan,China,Apr.19-24,2009.

[95]J.Ostergaard and D.E.Quevedo,“Multiple descriptions for packetized predictive control,”Eurasip Journal on Advances in Signal Processing,Article Number:45,Apr.2016.

[96]C.de Persis and A.Isidori,“Stabilizability by state feedback implies stabilizability by encoded state feedback,”Systems&Control letters,vol.53,no.3-4,pp.249-258,Nov.2004.

[97]C.de Persis,“n-Bit stabilization ofn-dimensional nonlinear systems in feedforward form,”IEEE Transactions on Automatic Control,vol.50,no.3,pp.299-311,Mar.2005.

[98]C.de Persis,“Nonlinear stabilizability via encoded feedback:The case of integral ISS systems,”Automatica,vol.42,no.10,pp.1813-1816,Oct.2006.

[99]C.de Persis and D.Nešić,“Practical encoders for controlling nonlinear systems under communication constraints,”Systems&Control Letters,vol.57,no.8,pp.654-662,Aug.2008.

[100]C.de Persis,“Minimal data rate stabilization of nonlinear systems over networks with large delays,”International Journal of Robust And Nonlinear Control,vol.20,no.10,pp.1097-1111,Jul.2010.

[101]Z.Qiu,L.Xie,and Y.Hong,“Quantized leaderless and leaderfollowing consensus of high-order multi-agent systems with limited data rate,”IEEE Transactions on Automatic Control,vol.61,no.9,pp.2432-2447,Sept.2016.

[102]D.E.Quevedo,A.Ahlen,and J.Ostergaard,“Energy efficient state estimation with wireless sensors through the use of predictive power control and coding,”IEEE Transactions on Signal Processing,vol.58,no.9,pp.4811-4823,Sept.2010.

[103]D.E.Quevedo,J.Ostergaard,and A.Ahlen,“Power control and coding formulation for state estimation with wireless sensors,”IEEE Transactions on Control Systems Technology,vol.22,no.2,pp.413-427,Feb.2014.

[104]M.Rabi,C.Ramesh,and K.H.Johansson,“Separated design of encoder and controller for networked linear quadratic optimal control,”SIAM Journal on Control and Optimization,vol.54,no.2,pp.662-689,2016.

[105]M.M.Rana,L.Li,and S.Su,“Distributed state estimation using RSC coded smart grid communications,”IEEE Access,vol.3,pp.1340-1349,2015.

[106]M.A.Rana,F.Ndiaye,S.A.Chowdhury,and N.Mansoor,“Multiple description image transmission for diversity systems over unreliable communication networks,”inProceedings of 10th International Conference on Computer and Information Technology,pp.240-244,Dhanmondi,Bangladesh,Dec.27-29,2007.

[107]A.Ribeiro and B.Giannakis,“Bandwidth-constrained distributed estimation for wireless sensor networks-Part I:Gaussian case,”IEEE Transactions on Signal Processing,vol.54,no.3,pp.1131-1143,Mar.2006.

[108]A.Ribeiro,B.Giannakis,and S.I.“Roumeliotis,SOI-KF:Distributed Kalman filtering with low-cost communications using the sign of innovations,”IEEE Transactions on Signal Processing,vol.54,no.12,pp.4782-4795,Dec.2006.

[109]A.J.Rojas,J.S.Freudenberg,J.H.Braslavsky,and R.H.Middleton,“Optimal signal to noise ratio in feedback over communication channels with memory,”inProceedings of the 45th IEEE Conference on Decision&Control,pp.240-244,San Diego,CA,USA,Dec.13-15,2006

[110]A.V.Savkin,“Analysis and synthesis of networked control systems:Topological entropy,observability,robustness and optimal control,”Automatica,vol.42,no.1,pp.51-62,Jan.2006.

[111]A.V.Savkin and T.M.Cheng,“Detectability and output feedback

stabilizability of nonlinear networked control systems,”IEEE Transactions on Automatic Control,vol.52,no.4,pp.730-735,Apr.2007.

[112]C.E.Shannon,“A mathematical theory of communication,”Bell System Technical Journal,vol.27,no.3,pp.379-423,Jul.1948.

[113]C.E.Shannon,“A mathematical theory of communication,”Bell System Technical Journal,vol.27,no.4,pp.623-666,Oct.1948.

[114]A.Shirazinia,A.A.Zaidi,L.Bao,and M.Skoglund,“Dynamic sourcechannel coding for estimation and control over binary symmetric channels,”IET Control Theory&Applications,vol.9,no.9,pp.1444-1454,Jun.2015.

[115]B.Shen,Z.Wang,D.Ding,and H.Shu,“H∞state estimation for complex networks with uncertain inner coupling and incomplete measurements,”IEEE Transactions on Neural Networks and Learning Systems,vol.24,no.12,pp.2027-2037,Dec.2013.

[116]B.Shen,Z.Wang,and H.Qiao,“Event-triggered state estimation for discrete-time multidelayed neural networks with stochastic parameters and incomplete measurements,”IEEE Transactions on Neural Networks and Learning Systems,vol.28,no.5,pp.1152-1163,May 2017.

[117]T.Sui,K.You,and M.Fu,“Kalman filtering with intermittent observations using measurements coding,”in10th IEEE International Conference on Control and Automation,pp.1127-1132,2013.

[118]T.Sui,K.You,M.Fu,and D.Marelli,“Stability of MMSE state estimators over lossy networks using linear coding,”Automatica,vol.51,pp.167-174,Jan.2015.

[119]P.Tallapragada and J.Cortes,“Event-triggered stabilization of linear systems under bounded bit rates,”IEEE Transactions on Automatic Control,vol.61,no.6,pp.1575-1589,Jun.2016.

[120]S.Tatikonda and S.Mitter,“Control-under communication constraints,”IEEE Transactions on Automatic Control,vol.49,no.7,pp.1056-1068,Jul.2004.

[121]V.A.Vaishampayan,“Design of multiple description scalar quantizers,”IEEE Transactions on Information Theory,vol.39,no.3,pp.8214-834,May 1993.

[122]V.A.Vaishampayan and J.C.Batllo,“Asymptotic analysis of multiple description quantizers,”IEEE Transactions on Information Theory,vol.44,no.1,pp.278-284,Jan.1998.

[123]J.Wang and H.Li,“Stabilization of a continuous linear system over channel with network-induced delay and communication constraints,”European Journal of Control,vol.31,pp.72-78,Sept.2016.

[124]F.Wang,J.Liang,Z.Wang,and X.Liu,“A variance-constrained approach to recursive filtering for nonlinear two-dimensional systems with measurement degradations,”IEEE Transactions on Cybernetics,in press.DOI:10.1109/TCYB.2017.2716400.

[125]L.Wang,Z.Wang,Q.-L.Han,and G.Wei,“Event-based varianceconstrainedH∞filtering for stochastic parameter systems over sensor networks with successive m issing measurements,”IEEE Transactions on Cybernetics,in press.DOI:10.1109/TCYB.2017.2671032.

[126]L.Wang,Z.Wang,Q.-L.Han,and G.Wei,“Synchronization control for a class of discrete-time dynamical networks with packet dropouts:a coding-decoding-based approach,”IEEE Transactions on Cybernetics,in press.DOI:10.1109/TCYB.2017.2740309.

[127]L.Wang,Z.Wang,T.Huang,and G.Wei,“An event-triggered approach to state estimation for a class of complex networks with mixed time delays and nonlinearities,”IEEE Transactions on Cybernetics,vol.46,no.11,pp.2497-2508,Nov.2016.

[128]L.Wang,Z.Wang,G.Wei,and F.E.Alsaadi,“Finite-time state estimation for recurrent delayed neural networks with component-based event-triggering protocol,”IEEE Transactions on Neural Networks and Learning Systems,in press.DOI:10.1109/TNNLS.2016.2635080.

[129]J.Wang and Z.Yan,“Coding scheme based on spherical polar coordi

nate for control over packet erasure channel,International Journal of Robust and Nonlinear Control,vol.51,pp.1159-1176,May 2014.

[130]X.Wang,E.E.Yaz,and J.Long,“Robust and resilient state-dependent control of discrete-time nonlinear systems with general performance criteria,”Systems Science&Control Engineering:An Open Access Journal,vol.2,pp.48-54,2014.

[131]W.Wei,S.Liu,Y.Song,and Y.Liu,“Probability-guaranteed setmembership filtering for systems with incomplete measurements,”Automatica,vol.60,pp.12-16,Oct.2015.

[132]G.Wei,S.Liu,L.Wang,and Y.Wang,“Event-based distributed setmembership filtering for a class of time-varying non-linear systems over sensor networks with saturation effects,”International Journal of General Systems,vol.45,no.5,pp.532-547,2016.

[133]N.Wiener,“Cybernetics:Or Control and Communication in the Animal and the Machine.”Paris,(Hermann&Cie)&Camb.Mass.(M IT Press),1948.

[134]W.S.Wong and R.W.Brockett,“Systems with finite communication bandwidth constraints-II:Stabilization with limited information feedback,”IEEE Transactions on Automatic Control,vol.44,no.5,pp.1049-1053,May 1999.

[135]J.Wu,H.Li,and X.Chen,“Leader-following consensus of nonlinear discrete-time multi-agent systems with limited communication channel capacity,”Journal of The Franklin Institute-Engineering and Applied Mathematics,vol.354,no.10,pp.4179-4195,Jul.2017.

[136]X.Xiao,L.Zhou,and G.Lu,“Detection of singular systems via a limited communication channel with m issing measurements capacity,”Information Sciences,vol.228,pp.192-202,Apr.2013.

[137]Y.Xu,C.Zhu,and L.Yu,“Multipath routing of multiple description coded images in wireless networks,”Journal of Computer Science and Technology,vol.29,no.4,pp.576-588,Jul.2014.

[138]K.You,“Control over communication networks:A personal perspective,”inProceedings of the 11th World Congress on Intelligent Control and Automation(WCICA’2014),pp.2002-2007,Shenyang,P.R.China,Jun.-Jul.2012.

[139]K.You,“Recursive algorithms for parameter estimation with adaptive quantizer,”Automatica,vol.52,pp.192-201,Feb.2015.

[140]K.You and L.Xie,“Network topology and communication data rate for consensusability of discrete-time multi-agent systems,”IEEETransactions on Automatic Control,vol.56,no.10,pp.2262-2275,Oct.2011.

[141]M.Yu,C.Yan,and D.Xie,“Event-triggered control for couple-group multi-agent systems with logarithmic quantizers and communication delays,”Asian Journal of Control,vol.19,no.2,pp.681-691,Mar.2017.

[142]W.Yu,G.Chen,and M.Cao,“Some necessary and sufficient conditions for second-order consensus in multi-agent dynamical systems,”Automatica,vol.46,no.6,pp.1089-1095,Jun.2010.

[143]Y.Yuan,P.Zhang,L.Guo,and H.Yang,“Towards quantifying the impact of randomly occurred attacks on a class of networked control systems,”Journal of the Franklin Institute-Engineering and Applied Mathematics,vol.354,no.12,pp.4966-4988,Aug.2017.

[144]S.Zhang,D.Ding,G.Wei,J.Mao,Y.Liu,and F.E.Alsaadi,“Design and analysis ofH∞filter for a class of T-S fuzzy system with redundant channels and multiplicative noises,”Neurocomputing,vol.260,pp.257-264,Oct.2017.

[145]S.Zhang,D.Ding,G.Wei,Y.Liu,and F.E.Alsaadi,“H∞state estimation for artificial neural networks over redundant channels,”Neurocomputing,vol.226,pp.117-125,Feb.2017.

[146]W.Zhang,S.Vedantam,and U.Mitra,“Joint transmission and state estimation:A constrained channel coding approach,”IEEE Transactions on Information Theory,vol.57,no.10,pp.7084-7095,Oct 2011.

[147]G.Zherlitsyn and A.S.Matveev,“M in-max optimal data encoding and fusion in sensor networks,”Automatica,vol.46,no.9,pp.1546-1552,Sept.2010.

[148]L.Zhou and G.Lu,“Detection and stabilization for discrete-time descriptor systems via a limited capacity communication channel,”Automatica,vol.45,no.10,pp.2272-2277,Oct.2009.

[149]L.Zou,Z.Wang,and H.Gao,“Set-membership filtering for timevarying systems with mixed time-delays under Round-Robin and Weighted Try-Once-Discard protocols,”Automatica,vol.74,pp.341-348,Dec.2016.

[150]L.Zou,Z.Wang,and D.H.Zhou,“Event-based control and filtering of networked systems:A survey,”International Journal of Automation and Computing,vol.14,no.3,pp.239-253,Jun.2017.