Residential Energy Scheduling for Variable Weather Solar Energy Based on AdaptiveDynamic Programming

Derong Liu,Yancai Xu,Qinglai Wei,,and Xinliang Liu

I.INTRODUCTION

ENERGY crisis has plagued humanity over the last century.Explosive growth of population depletes the limited traditional fossil fuels on the planet.In addition,burningfossil fuels have caused increasingly serious environmental problems,such as the pollution haze.Electricity is one of the most important energy forms for us,without which the motor of civilization would sputter and slow down.With growing population and rapid development of industrialization,the total consumption of electricity power goes higher and higher every year.Meanwhile,pollution of power plants continues to deteriorate.A broad consensus is widely reached on energy conservation to save the planet nowadays.Smart grid is an effective way to reduce the abuse of electricity.Many organizations and researchers have proposed meaningful work to achieve intelligent electrical energy saving[1]−[6].Great efforts have been made to electrical energy generation and transmission[7],[8],such as thermal power plants.The research on smart grid on the demand side is a systematic project.It mainly covers the renewable energy generation,the electrical energy transmission,the electrical energy storage,the distribution of electrical energy,and the optimization of household appliances.All the elements above are combined together to make the optimization process more difficult especially from the perspective of space complexity and computational complexity.On the demand side,there are many energy transmission directions.Therefore,some household appliances can be rescheduled to balance the total energy consumption.

Renewable energy resources are increasingly used around the world.The solar energy is the main part of renewable resources[9],[10].This energy can be converted to electrical current by photoelectric effect directly and conveniently[11].However,the converted electrical energy depends on weather conditions.For unstable generators,the demand side needs storage systems to maintain the balance of electrical energy.Besides,the intelligent energy scheduling is beneficial to make the produced energy effectively consumed.

Researchers have proposed many intelligent algorithms to solve sophiscated dynamic programming problems.Adaptive dynamic programming(ADP),which was proposed by Werbos,is an important approach for performance optimization with the characteristics of self-learning and adaptivity[12].It can be realized by finding the optimal control policy via Hamilton-Jacobi-Bellman(HJB)equation[13]−[20].Heuristic dynamic programming(HDP),action dependent heuristic dynamic programming(ADHDP),dual heuristic dynamic programming(DHP),action-dependent DHP(ADDHP),globalized DHP(GDHP),and action-dependent GDHP(ADGDHP)are all schemes of ADP[20],[21].Many scientists have carried out related works on ADP[22]−[26].Q-learning,proposed by Watkins and Dayan[27],was denoted as ADHDP[28]−[30].In recent years,Q-learning has been used in smart grid related energy systems.Researchers developed Q-learningbased approximation approach to solve the optimal control problem for smart grid in[31].Xuet al.used deterministic learning technique to achieve reinforcement learning output feedback control in[32].While in[33],Mohagheghiet al.used adaptive critic designs/ADP to find the optimal controller.Moreover,some dynamic programming approaches,adaptive fuzzy control methods and genetic algorithms were used to realize smart grid energy resources scheduling in[34]−[36].Via output feedback,Liet al.achieved adaptive fuzzy control of nonstrict feedback systems,especially when there are unmodeled dynamics and fuzzy dead zone[37].Huang and Liu used ADP to achieve battery control[38].Thereafter,Boaroet al.also realized the residential energy management by ADP[39],[40].Weiet al.achieved optimal battery sequential control scheme for smart home energy systems in[41].In addition,ADP was applied to other systems,such as coal gasification,wind farm power system stability control,reactive power control,and air-breathing hypersonic vehicle tracking control[16],[26],[42]−[44].

The residential energy scheduling is a complicated dynamic programming problem.The scheduling object is a nonlinear,time-varying,indefinite and complex system.All elements must be addressed together such as the real-time price,the changing solar power,the household loads and the batteries’energy level in the adjacent housing units.This paper is an upgraded version of the previous one with home energy interexchange[45].Solar energy is also taken into account for the residential energy scheduling,which increases the complexity of the scheduling.Meanwhile,each electricity-consuming device(batteries and loads)can be supplied by one or more resources.The newly proposed residential energy scheduling algorithm is implemented by training three ADHDP networks based on weather types.Moreover,the algorithm has the capability to keep adapting and improving as new data comes in all the time.

The rest of this paper is organized as follows.Section II describes the residential energy scheduling problem.In Section III,the theory of ADHDP is briefly introduced to solve complicated dynamic problems.The detailed ADHDP-based residential energy scheduling algorithm is analyzed step by step.In Section IV,the experimental simulations show the related energy-saving results.Conclusions are drawn in Section V with a few remarks and future work.

II.RESIDENTIAL ENERGY MANAGEMENT

A.Notation

A summary of notation is as follows.

B.Components of Residential Energy Management

The residential energy scheduling system includes n housing units,a public utility grid and a power management unit(PMU).Within each housing unit,there are a solar power station,an energy storage system and a residential load.All the energy-related devices are connected and managed by the PMU,which is shown in Fig.1.The solar power stations produce electrical energy.Then the energy will be sent to residential loads,batteries and the utility grid according to a priority order.The arrows show the direction of electricity transmission(bidirectional/unidirectonal).Batteries are used to store and buffer electrical energy.Excessive energy will be transmitted to the utility grid with a lower price.

Fig.1.The residential energy scheduling system.

The PMU is the vital center to guide the energy transmission.With MOSFET and thyristor devices,the AC/DC conversion can be achieved.Then processors inside the PMU can find an appropriate solution depending on situations.Solar power stations generate electrical energy,while batteries store energy,and residential loads consume electrical energy.

C.Weather-type Classification

The solar power stations generate electricity from the sun.Therefore,different weather conditions may have different effects on generating solar power.The most important factors of solar power are the intensity of sunlight and operating temperature.In order to realize weather forecast,the weather conditions are divided into three categories:sunny,partly cloudy and cloudy.Fig.2(a)shows the one-month weathertype classification of Braedstrup,Denmark in July 2006.The classification is carried out based on the weather forecast and the 24-hour solar power prediction[46],[47].The main factors are the solar irradiance,total cloud amount and low cloud amount.Sunny days mean high solar irradiance,low total cloud amount and low low cloud amount.In contrast,low solar irradiance,high total cloud amount and high low cloud amount make cloudy days.Detailed classification can be found in[47].Different values mean different weather types.The predicted solar power output can help to determine the corresponding weather type.

D.Solar Power

Solar energy is regarded as one of the most important forms of renewable energies.Solar power stations absorb solar radiation and excite electrons so as to generate electricity[48].The solar power output was provided by a Photovoltaics(PV)system in Braedstrup city of Denmark(55.970°N,9.612°E)[49].In order to match the solar power stations,the data is processed with one-hour interval.The solar energy power of solar station 1 in one week is shown in Fig.2(b).

E.Residential Real-Time Pricing and Load Pro file

Residential real-time pricing is an efficient tool for optimized electricity allocation.In actual applications,it encourages electricity consumers to shift loads according to the residential real-time price(RRTP),usually from heavyload hours to light-load hours,which helps balance loads of the public utility grid.Residential real-time pricing usually corresponds to the real-time loads of the utility grid.The oneday residential real-time price is shown in Fig.2(c),which was acquired and processed from[50].The penalty price is to value the usage of batteries’energy with an opposite tendency of RRTP.The resell price for selling excessive energy to the utility grid is lower than the RRTP.The residential loads are mainly from the usage of daily household appliances.Each housing unit has its own appliances.The one-week residential load 1 is shown in Fig.2(d)obtained from[51].Spikes means peak energy periods which reflects the actual situation.The RRTP and the residential loads are discretized in hourly spans for the convenience of calculation and prediction.

F.Storage Batteries

Considering the energy transmission loss factors,the derived efficiency equation in storage systems can be expressed as[52]

Some constraints are given to meet reality as much as possible.

a)Upper and lower energy bounds

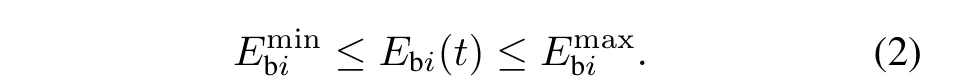
b)Maximum charge/discharge power limits

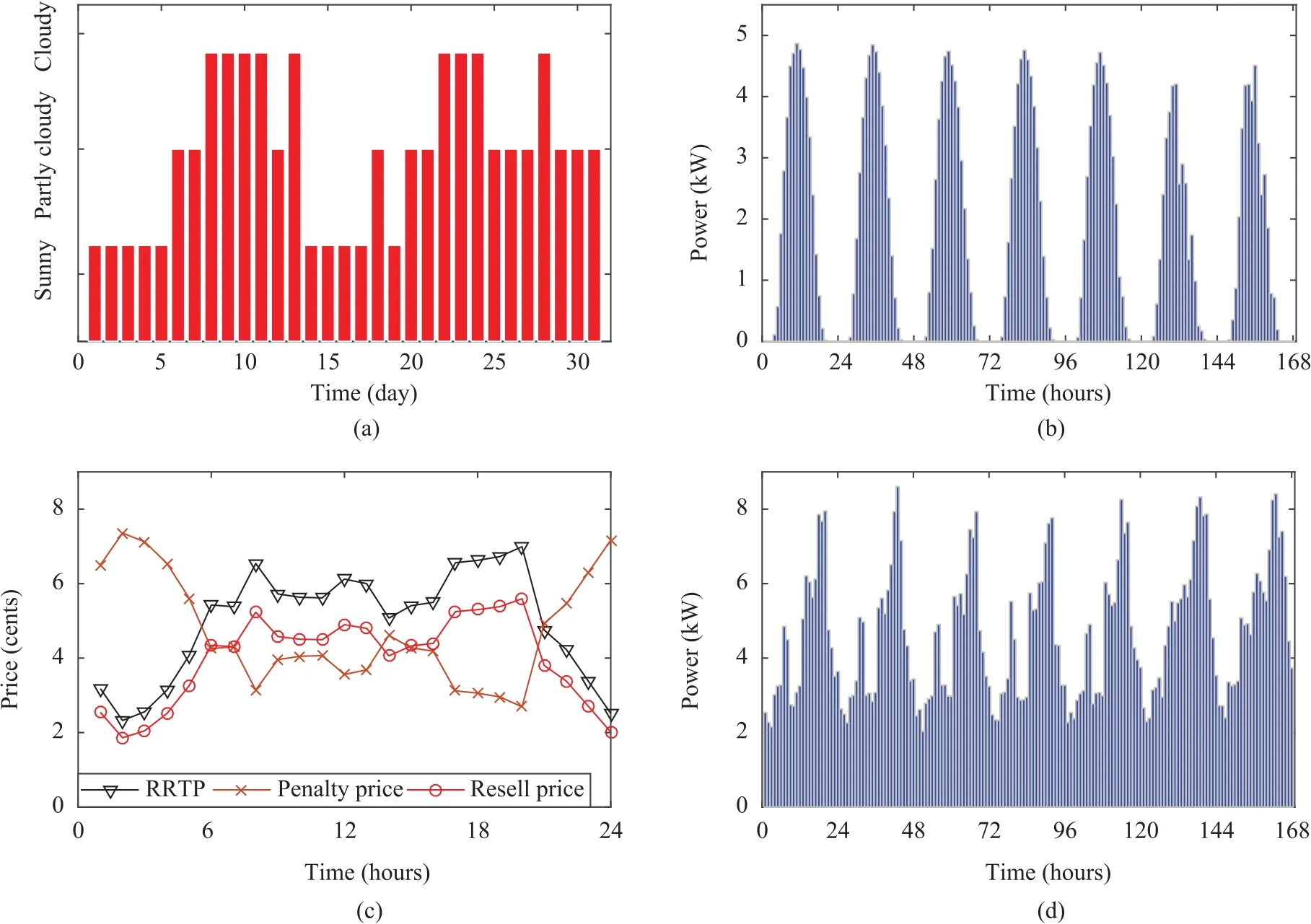
Fig.2.(a)Weather-type classification of Braedstrup in July 2006.(b)Solar energy power(solar station 1)in one week.(c)Residential real-time price,resell price and penalty price in one day.(d)Residential load(load 1)in one week.

c)Real time residential load balance

III.RESIDENTIAL ENERGY SCHEDULING

The residential energy scheduling is proposed to solve the energy management problem with solar energy based on ADHDP.This section introduces the ADHDP and energy management strategy.

A.Action Dependent Heuristic Dynamic Programming

ADHDP is a very useful tool for solving optimization and control problems by employing the principle of optimality[53].This subsection will present a brief introduction of ADHDP.

The Bellman principle of optimality is used to solve problems of dynamic programming,which solves optimization problems in a recursive manner and works backward in realtime for scheduling problems[53],[54].The value function in one period and the next period are then obtained and described by the Bellman equation.De fine the discrete-time nonlinear dynamic system as

With the help of transition functionF(x(k),u(k),k)and control actionu(k),the relationship between the next stateandx(k)is obvious.Suppose the associated performance index/cost function as

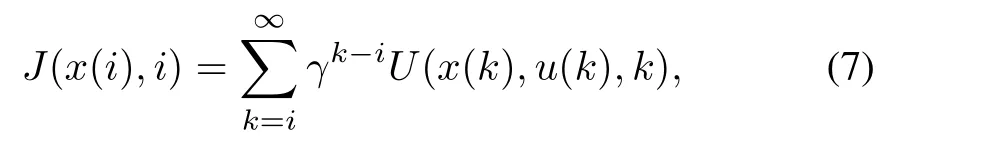
where the performance index/cost functionJ(x(i),i)is the sum of all the utility function multiplied by appropriate powers of the discount factor.Finding an appropriate control sequenceu(k),k=i,i+1,...is the key to minimize the performance index functionJ(x(i),i).According to the Bellman principle of optimality,the optimal cost at timekis

The optimal control sequence is

For discrete-time systems,the optimization process of ADHDP is done by working backward in time[53].ADHDP solves dynamic programming problems through policy improvement and policy evaluation.For the discrete energy scheduling problem,it can be handled by finding the optimal control sequence with the help of neural networks[38].Fig.3 reveals the ADHDP architecture for residential energy scheduling.

B.Solar Energy

Fig.3.ADHDP architecture of residential energy scheduling with solar energy.

The generated solar energy changes with the intensity of sunlight and the temperature.The solar power stations transmit electricity to other energy receivers.The solar energy receivers are housing loadi,batteryiand the outside public utility grid.In order to utilize the generated electrical energy as much as possible,the receivers of the solar energy have different priorities.The energy receivers’priorities are listed in Table I.Energy loss exists during the processes of AC→DC/DC→AC conversions and batteries’charge/discharge.Therefore,household loads have higher precedence than batteries.Batteries have higher priorities than the outside public utility grid.Besides,solar power stations meet the load or the battery on its own side first based on the principle of contiguity.Thus,household loaditakes precedence over household loadi+1.

TABLE I PRIORITIES OF ENERGY RECEIVERS(SOLARi)

C.Batteries’Control Strategy

There arenstorage devices(batteries)separately innhousing units.Each battery has 4 states(1,0,−1,−2).During the application,the batteries can provide electrical energy to any housing load.However,in this paper,batteries are primarily responsible for the housing loads on its own side.Letuibe the states of batteryi.Whenui=1,batteryiis charging by the utility grid or solari.Ifui=0,batteryiis idle without any action.Whileui=−1,batteryioutputs energy to the housing load on its own side.For example,ifui=−1,batteryionly serves the household loadi.Asui=−2,batteryioutputs energy to the utility grid.

In order to reduce the loss during transmissions,the residential solar powerPsolari(t)is primarily used to fulfill the residential loadPloadi(t).If there is surplus solar power left,the extra power will be used to charge batteryior output to the internal line correspondingly.While the residential solar powerPsolari(t)cannot satisfy the residential loadPloadi(t),batteryior/and the internal line will supply additional energy to meet the need of residential loadPloadi(t).The detailed batteries’control strategy is shown in Table II.As the computation interval is one hour,CAbi(t)andhave the same unit of measurement.

D.Goal of Optimization

Taking the RRTP into consideration,the ADHDP-based residential energy scheduling is carried out to find appropriate control actions of batteries so as to reduce the electrical energy cost.Therefore,the optimization function(10)is composed of three parts:the cost of buying from the utility grid,the cost of selling solar energy to the utility grid(negative)and the penalty cost.The penalty cost is to promote the usage of batteries where the penalty priceCschanges in an opposite trend compared with the residential real-time price.As a result,with the help of the penalty cost,the batteries always try to go through a complete cycle of charge and discharge,

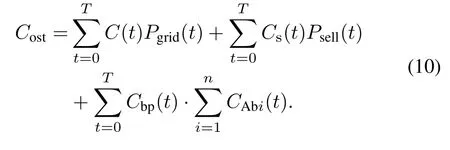
E.ADHDP-Based Residential Energy Scheduling Algorithm With Solar Energy

As can be seen from Fig.3,the initially prepared data contains the RRTP,sell-back price,penalty price,household loads and solar power.The critic networks are trained and improved with the equationwhereQ(t)is the output of critic networks.Afterwards,the critic networks will be upgraded with the training processDuring the ADHDP training process,the utility function are calculated as

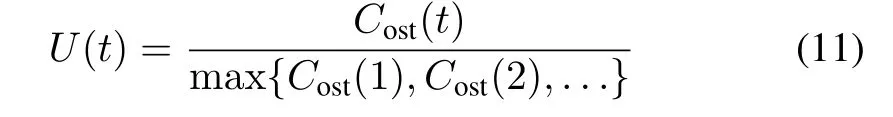
where

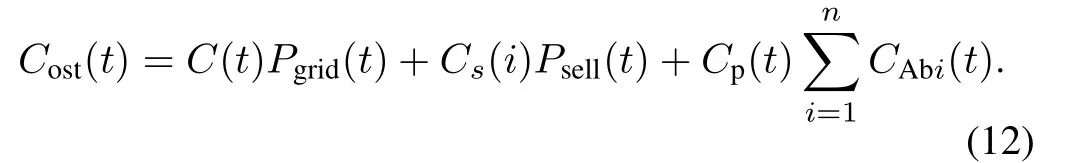
There are three kinds of weather types classified artificially depending on the relationship between the solar power and theintensity of sunlight.Based on the current accurate weather forecast,each day can be categorized into the three weather types:sunny,partly cloudy and cloudy.The intensity of sunlight is the main determinant of solar power production.Therefore,the windy,rainy or snowy weather are meaningless here.

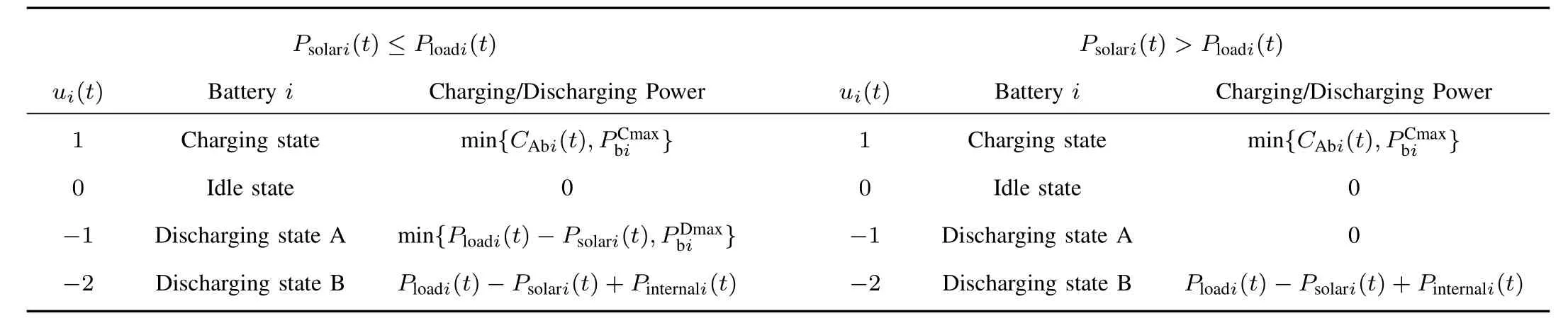
TABLE II BATTERIES’CONTROL STRATEGY

Three types of weather conditions imply three kinds of residential energy scheduling problem.Thus,the one-month residential energy scheduling needs three ADHDP-based neural networks(ADHDP networks).Every ADHDP network has to be trained during the 24 hour period.It has to be noticed that the energy status has to go across smoothly and perfectly between two adjacent days.Table III lists all the days of each category in July 2006.

TABLE III CATEGORIES OF THREE WEATHER TYPES

The structure of the detailed ADHDP-based residential energy scheduling algorithm is summarized in Fig.4.It is obvious that the prepared data is processed in the initialization of 3 ADHDP networks.ADHDP-1,ADHDP-2 and ADHDP-3 are three separate ADHDP networks which are trained in their corresponding weather types.The detailed training algorithm is shown as follows(Algorithm 1).

1)The ADHDP-based residential energy scheduling algorithm initializes 3 ADHDP networks.Then,the collected data needs to be preprocessed to meet the requirements of the ADHDP networks.The data includes the operation parameters and the systems states,such as the RRTP,the penalty price,weather types and solar powers.

2)Determine each day’s weather type.Accordingly,the data of the classified days goes to the corresponding ADHDP networks(ADHDP-1/2/3).After the training process,the optimal control sequences of batteries can be found to guide energy transmissions.Meanwhile,other parameters will be calculated such as the cost of buying electricity,the cost of selling electricity and the penalty cost.One important thing to note about this step is that the network weights should be saved for next time to use with the same weather type.Moreover,the batteries’remaining capacities should be continuous between days.

3)Improve the ADHDP-based residential energy scheduling networks continuously.With the incoming training data,the ADHDP networks can be trained and adapted to meet new requirements continuously.

Thereafter,the trained algorithm has the ability to guide the residential energy scheduling and evolve during applications.

Remark 1:This ADHDP-based residential energy scheduling algorithm is inspired by the original paper[45].The solar energy is incorporated into the residential energy scheduling problem.Besides,new energy usage priorities are applied.The weather type based algorithm has proposed a valid method to the solar-related energy scheduling.Therefore,this algorithm has many innovative ideas.

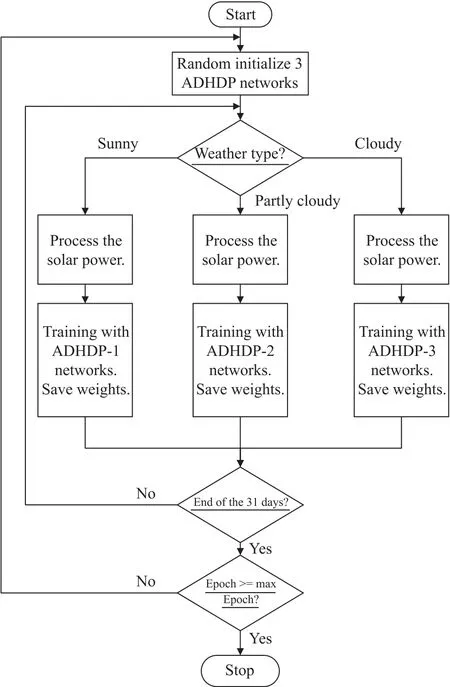
Fig.4.The ADHDP-based residential energy scheduling algorithm.

Algorithm 1:ADHDP-based residential energy scheduling algorithm

Part I:Initialization

Step 1:Collect data and pre-process them which include the RRTP,the penalty price,the weather types and the solar power.

Step 2:Give the computation precisionε＞0 and the maximum number of loops.

Step 3:Initialize three ADHDP networks,which are ADHDP-1,ADHDP-2,and ADHDP-3.

Step 4:Give the basic parameters for the ADHDP-based residential energy scheduling algorithm.

Part II:Iteration

Step 5:Begin the loop and determine which weather type it belongs to.

Step 6:Process the solar energy with their priorities.

Step 7:Select control strategies for batteries randomly.Train the corresponding ADHDP-1/2/3 networks within a specified day and try to find the best control strategy.Afterwards,save and pass the best weights to the next training.

Step 8:Determine whether it is the end of the month.If so,go to the next step.Otherwise,go to Step 5.

Step 9:Determine whether it is the maximum epoch.If so,go to the next step.Otherwise,go to Step 3 and repeat the process.

Step 10:Pick the best ADHDP networks and calculate the cost.

Step 11:Evolve in applications.

IV.SIMULATIONS

The ADHDP-based residential energy scheduling is designed to solve energy transmission problems between housing units and the utility grid.It is a complicated problem for the multiple energy transmission directions.Inside housing uniti,solar powerigives energy;household loadiabsorbs energy;batteryiis a local energy buffer device.Moreover,energy can be transferred between devices of housing units and the utility grid.All the energy transmissions are via the PMU.Here we taken=2 to do the simulations(i=1,2),which means the simulation scenario is designed with two housing units.

In the simulation scenario,batteries 1 and 2 are the same at the beginning with the capacities of 50 kW·h.Considering the actual transmission process and cost,their maximum charging and discharging rate are 5kW.The initial batteries’status is 80%of the capacities.While the batteries have a minimum capacity(10%of the capacities)to protect themselves.Two household loads have similar features.Everyday,there is a load spike during the day(seen in Fig.5(a))which reveals people’s physical-activity routines.Another bigger spike appears during the nighttime when people cook and do recreational activities before bedtime.The household loads are smoother on the weekends than on weekdays for people have more freedom to dispose time.The solar power stations generates electricity,which can be seen in Fig.5(a).The solar power data comes from the roofed solar station in Braedstrup,Denmark.Besides,the period of the data is in July 2006.Each solar power has the maximum output of no more than 6kW.Solar 2 outputs more solar energy than solar 1.From Fig.5(a),it is obvious that the power output changes with the solar radiation.During the midnight,its output is zero.However,when the intensity of sunlight becomes stronger,the output power gets higher.The outside public utility grid is assumed to have enough power to recover the absent electricity power.

In the ADHDP-based residential energy scheduling algorithm,structures of critic networks(ADHDP-1,ADHDP-2,ADHDP-3)are all 9-20-1.The 9 inputs include the RRTP,two batteries’energy status,two household loads,two solar energy status and two control actions(u1,u2).Their hidden layers have 20 neurons,and the aim of the output layer is to minimize the total cost.The one month period is separated into three parts in Table III.Therefore,three different ADHDP networks have to be trained accordingly to acquire their corresponding features.The simulation is processed in the environment of Matlab R2015b on a DELL computer running Windows 10 Pro 64-bit OS with Intel Core i5 CPU@3.2GHz and 8GB ram.

After one-month simulation of residential energy scheduling,results show that the batteries go through a cycle of charge and discharge everyday in Fig.5(b).It is quite obvious that batteries,as the buffering energy storage devices,prefer to buy and store electrical energy while the RRTP is low.The high price of the RRTP will depress the energy supply from the outside public utility grid so as to save money.However,when it comes to the renewable solar energies,their output characteristics change the results especially during the noon hours.With the peak intensity of sunlight during the noon hours,the solar generators output the most energy exceeding current loads’energy demand.Therefore,the solar generators output extra energy to batteries and the utility grid according to their priorities which explains the full charge capacities of batteries during the middle of the day.According to Fig.4,the solar energy will be handled first.Thereafter,battery energy will be scheduled to their targets.In addition,the parts of household loads,which are not satisfied by the solar generators and batteries,will be powered by the outside public utility grid.

The scale and scope of the one-month simulation are too large to interpret.Thus,three days(July 1,July 6 and July 8 in 2006)are selected from the whole month on behalf of the three ADHDP simulation networks.In Fig.6,the sunny type(July 1,2006)has a smooth training and learning process.The cycle of charge and discharge is clear at the beginning and end points.Besides,the solar generation keeps smooth without sharp changes in sunny days.During the noon hours,the solar energy will be enough to fully charge batteries.However,the partly cloudy type influences the solar energy generation a little bit and the batteries’energy has a wide range of fluctuation.Moreover,cloudy days cause some difficulties in training of the ADHDP network since there is not much solar energy for batteries.

Figs.7 and 8 give the detailed control actions for the two batteries(u1,u2).On sunny days,the generated solar energy can meet most of the household requirements and charge the batteries.However,when weather gets worse,the batteries have to take more responsibility to meet users’requirements.Besides,battery 1 has higher priority than battery 2 when conflicts happen,so battery 1 discharges more energy than battery 2 more often.

Fig.5.(a)Pretreated data(housing unit 1)in one week.(b)Remaining capacity of battery 1 and remaining power of load 1 powered by the utility grid in one week.

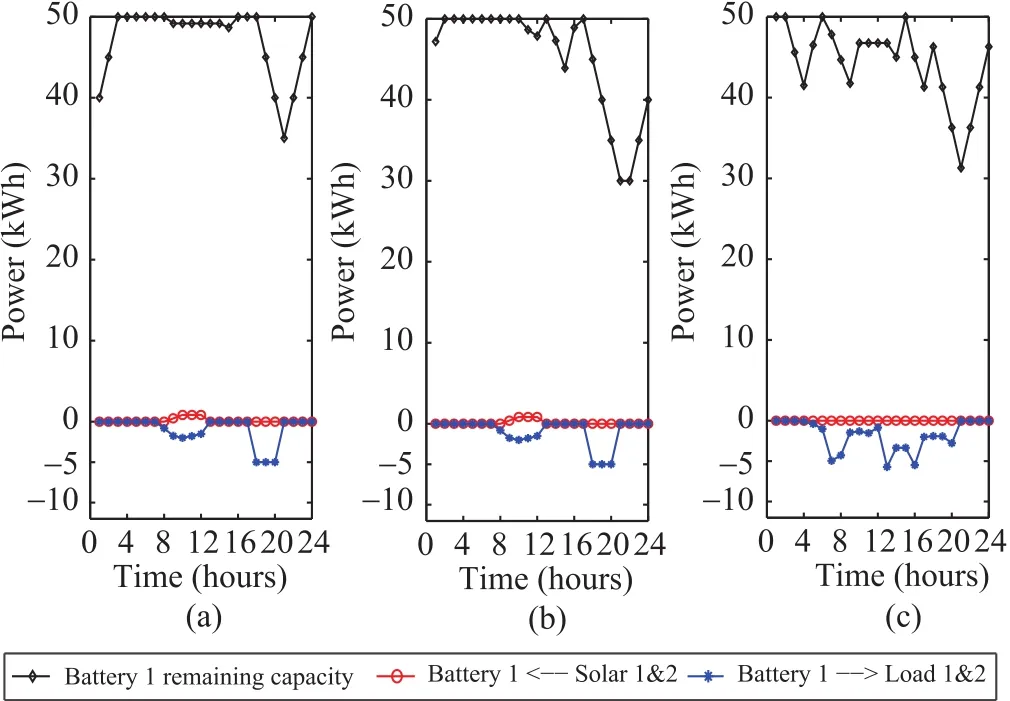
Fig.6.Comparison among three types of ADHDP networks.(a)Sunny on July 1,2006.(b)Partly cloudy on July 6,2006.(c)Cloudy on July 8,2006.

During each time step,the household loads may acquire energy from one or more energy resources according to their priorities.Figs.9 and 10 show the sources and compositions of energy needed to load 1 and load 2.Different colors are used to illustrate different compositions and their corresponding portions.To household loads 1 and 2,their primary energy source is the solar energy,followed by the battery energy and the grid energy.It also can be noticed that in sunny days,the solar energy occupies a large portion of the whole loads and the utility grid is used when the RRTP is low so as to save the electricity cost.While in partly cloudy or cloudy days,the solar portion becomes smaller.The batteries and the utility grid are used more often to compensate for the lack of solar energy.

Particle swarm optimization(PSO)is an intelligent optimization method,which has good optimization results in solving nonlinear problems[55].A PSO method is applied in this section to optimize the residential energy scheduling problem,as a comparison.The position of every particlezi(t)and the velocity vectorvi(t)at timetare calculated as follows.

The utility function to be minimized is defined as

The parameters used are listed below:

Swarm size 30.

Iteration 120.

Inertia factorw=7.

ρ1,ρ2=1.0.

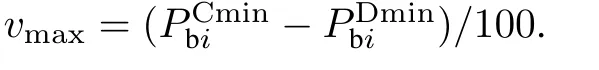
Fig.7.Control actions of battery 1 with three weather types.(a)Sunny on July 1,2006.(b)Partly cloudy on July 6,2006.(c)Cloudy on July 8,2006.

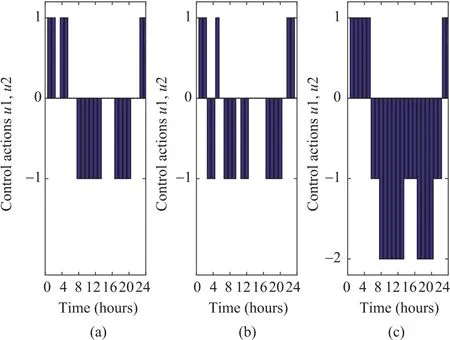
Fig.8.Control actions of battery 2 with three weather types.(a)Sunny on July 1,2006.(b)Partly cloudy on July 6,2006.(c)Cloudy on July 8,2006.

Fig.9.Energy sources to load 1.(a)Sunny on July 1,2006.(b)Partly cloudy on July 6,2006.(c)Cloudy on July 8,2006.

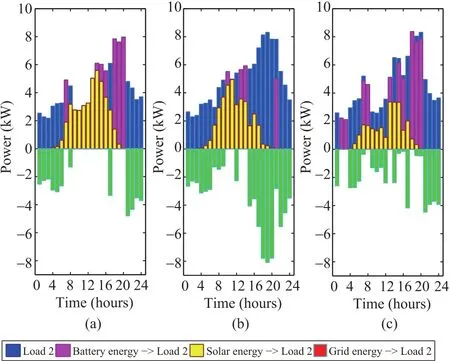
Fig.10. Energy sources to load 2.(a)Sunny on July 1,2006.(b)Partly cloudy on July 6,2006.(c)Cloudy on July 8,2006.

After 120 times of iterations,the PSO algorithm stops with the data shown in Table IV.The ADHDP-based residential energy scheduling method has achieved the aim of energyscheduling and money-saving,with the cost of buying electrical energy from the utility grid 75569 cents in a whole month(30.7%saved).In contrast,the PSO algorithm costs 80476 cents in a month(26.2%saved).Besides,this ADHDP scheduling method sells excessive solar energy to the outside public utility grid.After simulations,the income of reselling to the grid is 366.10 cents with the reselling real time price as 80%of the RRTP.The number of reselling actions totals 34 times.Hence,the optimization goal of residential energy scheduling has been achieved.The house owners can save the electricity cost and protect the environment in the long run.

TABLE IV COMPARISON OFPSOANDADHDP

V.CONCLUSION

This paper presents a residential energy scheduling method to solve the energy intelligent transmission problem.The smart micro grid has many housing units with sets of energyrelated equipments.Following the trend of saving energy and easing the burden of the grid,RRTP is imperative.Renewable resources can also be built by residents.All the factors increase the complexity of the energy transmission.The residential energy scheduling method can solve the problem with ADHDP.The main contributions of this paper are as follows:

1)Weather forecast is adopted in the scheduling as it is ripe for applications.Therefore,the method is designed based on three weather types(sunny,partly cloudy,cloudy).Each day can be categorized into three types which have different effects on solar power generators.

2)All the energy-consuming equipment can be supplied by one or more energy resources.

3)The ADHDP-based residential energy scheduling method has designed three corresponding ADHDP neural networks to manage all the electrical energy flows.Simulation results have proven its effectiveness with 30.7%cost-saving.

4)The proposed ADHDP scheduling algorithm works better than the PSO algorithm.

5)The designed method has the ability to evolve in applications.The three ADHDP neural networks can learn and change accordingly during application.In addition,the weather forecast can help to determine the weather type beforehand.

Overall,the ADHDP-based residential energy scheduling can help achieve the grid load balance and reduce the cost spent on electrical energy.Future work will cover the energy management between different smart micro grids and other intelligent algorithms.

[1]P.Palensky and D.Dietrich,“Demand side management:Demand response,intelligent energy systems,and smart loads,”IEEE Transactions on Industrial Informatics,vol.7,no.3,pp.381−388,Jun.2011.

[2]A.Chaouachi,R.M.Kamel,R.Andoulsi,and K.Nagasaka,“Multiobjective intelligent energy management for a microgrid,”IEEE Transactions on Industrial Electronics,vol.60,no.4,pp.1688−1699,Apr.2013.

[3]B.Huang,Y.Li,H.Zhang,and Q.Sun,“Distributed optimal co-multimicrogrids energy management for energy internet,”IEEE/CAA Journal of Automatica Sinica,vol.3,no.4,pp.357−364,Oct.2016.

[4]Q.Dong,L.Yu,W.Song,J.Yang,Y.Wu,and J.Qi,“Fast Distributed Demand Response Algorithm in Smart Grid,”IEEE/CAA Journal of Automatica Sinica,vol.4,no.2,pp.280−296,Apr.2017.

[5]M.R.Alam,M.St-Hilaire,and T.Kunz,“Computational Methods for Residential Energy Cost Optimization in Smart Grids:A Survey,”ACM Computing Surveys,vo,.49,no.1,pp.1−34,Jul.2016.

[6]Z.Hong,R.Wang,and X.Li,“A clustering-tree topology control based on the energy forecast for heterogeneous wireless sensor networks,”IEEE/CAA Journal of Automatica Sinica,vol.3,no.1,pp.68−77,Jan.2016.

[7]R.Hemmati,R.A.Hooshmand,and A.Khodabakhshian,“Coordinated generation and transmission expansion planning in deregulated electricity market considering wind farms,”Renewable Energy,vol.85,pp.620−630,Jan.2016.

[8]F.Zhao,C.Zhang,B.Sun,“Initiative optimization operation strategy and multi-objective energy management method for combined cooling heating and power,”IEEE/CAA Journal of Automatica Sinica,vol.3,no.4,pp.385−393,Oct.2016.

[9]M.S.Hossain,N.A.Madlool,N.A.Rahim,J.Selvaraj,A.K.Pandey,and A.F.Khan, “Role of smart grid in renewable energy:An overview,”Renewable and Sustainable Energy Reviews,vol.60,pp.1168−1184,Jul.2016.

[10]J.Chen and F.Yang,“Data-driven subspace-based adaptive fault detection for solar power generation systems,”IET Control Theory&Applications,vol.7,no.11,pp.1498−1508,Jul.2013.

[11]U.S. Department of Energy, http://www.energy.gov/scienceinnovation/energy-sources/renewable-energy/solar, avaibable online Dec.2015.

[12]P.J.Werbos,“Approximate dynamic programming for real-time control and neural modeling,”inHandbook of Intelligent Control:Neural,Fuzzy,and Adaptive Approaches,D.A.White and D.A.Sofge,Editors.New York:Van Nostrand Reinhold,Chapter 13,1992.

[13]A.Heydari and S.N.Balakrishnan,“Finite-horizon control-constrained nonlinear optimal control using single network adaptive critics,”IEEE Transactions on Neural Networks and Learning Systems,vol.24,no.1,pp.145−157,Jan.2013.

[14]Q.Wei,R.Song,and P.Yan,“Data-driven zero-sum neuro-optimal control for a class of continuous-time unknown nonlinear systems with disturbance using ADP,”IEEE transactions on Neural Networks and Learning Systems,vol.27,no.2,pp.444−458,Feb.2016.

[15]Q.Wei and D.Liu,“A novel iterativeθ-Adaptive dynamic programming for discrete-time nonlinear systems,”IEEE Transactions on Automation Science and Engineering,vol.11,no.4,pp.1176−1190,Oct.2014.

[16]Q.Wei and D.Liu,“Adaptive dynamic programming for optimal tracking control of unknown nonlinear systems with application to coal gasification,”IEEE Transactions on Automation Science and Engineering,vol.11,no.4,pp.1020−1036,Oct.2014.

[17]Q.Wei,D.Liu,and Y.Xu,“Neuro-optimal tracking control for a class of discrete-time nonlinear systems via generalized value iteration adaptive dynamic programming approach,”Soft Computing,vol.20,no.2,pp.697−706,Feb.2016.

[18]H.He,Z.Ni,and J.Fu,“A three-network architecture for on-line learning and optimization based on adaptive dynamic programming,”Neurocomputing,vol.78,no.1,pp.3−13,Feb.2012.

[19]H.Li,L.Wang,H.Du,and A.Boulkroune,“Adaptive fuzzy backstepping tracking control for strict-feedback systems with input delay,”IEEE Transactions on Fuzzy Systems,vol.25,no.3,pp.642−652,Jun.2017.

[20]Q.Wei,D.Liu,and G.Shi,“A novel dual iterative Q-learning method for optimal battery management in smart residential environments,”IEEE Transactions on Industrial Electronics,vol.62,no.4,pp.2509−2518,Apr.2015.

[21]D.V.Prokhorov and D.C.Wunsch, “Adaptive critic designs,”IEEE Transactions on Neural Networks,vol.8,no.5,pp.997−1007,Sep.1997.

[22]J.J.Murray,C.J.Cox,G.G.Lendaris,and R.Saeks,“Adaptive dynamic programming,”IEEE Transactions on Systems,Man,and Cybernetics,Part C:Applications and Reviews,vol.32,no.2,pp.140−153,May 2002.

[23]B.Luo,H.Wu,and T.Huang,“Off-policy reinforcement learning for H∞control design,”IEEE Transactions on Cybernetics,vol.45,no.1,pp.65−76,Jan.2015.

[24]Y.Jiang and Z.P.Jiang,“Robust adaptive dynamic programming and feedback stabilization of nonlinear systems,”IEEE Transactions on Neural Networks and Learning Systems,vol.25,no.5,pp.882−893,May 2014.

[25]Q.Wei and D.Liu,“Numerical adaptive learning control scheme for discrete-time non-linear systems,”IET Control Theory&Applications,vol.7,no.11,pp.1472−1486,Jul.2013.

[26]Y.Tang,H.He,J.Wen,and J.Liu,“Power system stability control for a wind farm based on adaptive dynamic programming,”IEEE Transactions on Smart Grid,vol.6,no.1,pp.166−177,Jan.2015.

[27]C.Watkins and P.Dayan, “Q-learning,”Machine Learning,vol.8,no.3/4,pp.279−292,May 1992.

[28]F.L.Lewis,D.Vrabie,and K.G.Vamvoudakis,“Reinforcement learning and feedback control:Using natural decision methods to design optimal adaptive controllers,”IEEE transactions on Control Systems Technology,vol.32,no.6,pp.76−105,Dec.2012.

[29]F.L.Lewis and D.Vrabie,“Reinforcement learning and adaptive dynamic programming for feedback control,”IEEE Circuits and Systems Magazine,vol.9,no.3,pp.32−50,Aug.2009.

[30]Q.Wei and D.Liu,“A novel policy iteration based deterministic Q-learning for discrete-time nonlinear systems,”Science China Information Sciences,vol.58,no.12,pp.122203:1−122203:15,Dec.2015.

[31]Y.Liang,L.He,X.Cao,and Z.J.Shen,“Stochastic control for smart grid users with flexible demand,”IEEE Transactions on Smart Grid,vol.4,no.4,pp.2296−2308,Dec.2013.

[32]B.Xu,C.Yang,and Z.Shi,“Reinforcement learning output feedback NN control using deterministic learning technique,”IEEE Transactions on Neural Networks and Learning Systems,vol.25,no.3,pp.635−641,Mar.2014.

[33]S.Mohagheghi,G.K.Venayagamoorthy,and R.G.Harley,“Fully evolvable optimal neurofuzzy controller using adaptive critic designs,”IEEE Transactions on Fuzzy Systems,vol.16,no.6,pp.1450−1461,Dec.2008.

[34]Y.Riffonneau,S.Bacha,F.Barruel,and S.Ploix,“Optimal power flow management for grid connected PV systems with batteries,”IEEETransactions on Sustainable Energy,vol.2,no.3,pp.309−320,Jul.2011.

[35]D.K.Maly and K.S.Kwan,“Optimal battery energy storage system(BESS)charge scheduling with dynamic programming,”IEEE Proceedings-Science,Measurement and Technology,vol.142,no.6,pp.453−458,Nov.1995.

[36]C.Chen,S.Duan,T.Cai,and B.Liu,“Energy trading model for optimal microgrid scheduling based on genetic algorithm,”inProceedings of IEEE 6th International Power Electronics and Motion Control Conference,Wuhan,China,Jul.2009,pp.2136−2139.

[37]L.Wang,H.Li,Q.Zhou,and R.Lu,“Adaptive fuzzy control for nonstrict feedback systems with unmodeled dynamics and fuzzy dead zone via output feedback,”IEEE Transactions on Cybernetics,vol.47,no.9,pp.2400−2412,Sep.2017.

[38]T.Huang and D.Liu,“A self-learning scheme for residential energy system control and management,”Neural Computing and Applications,vol.22,no.2,pp.259−269,Feb.2013.

[39]M.Boaro,D.Fuselli,F.D.Angelis,D.Liu,Q.Wei,and F.Piazza,“Adaptive dynamic programming algorithm for renewable energy scheduling and battery management,”Cognitive Computation,vol.5,no.2,pp.264−277,Jun.2013.

[40]D.Fuselli,F.D.Angelis,and M.Boaro,“Action dependent heuristic dynamic programming for home energy resource scheduling,”International Journal of Electrical Power and Energy Systems,vol.48,no.1,pp.148−160,Jun.2013.

[41]Q.Wei,D.Liu,Y.Liu,and R.Song,“Optimal constrained self-learning battery sequential management in microgrid via adaptive dynamic programming,”IEEE/CAA Journal of Automatica Sinica,vol.4,no.2,pp.168−176,Apr.2017.

[42]Y.Tang,H.He,Z.Ni,J.Wen,and X.Sui,“Reactive power control of grid-connected wind farm based on adaptive dynamic programming,”Neurocomputing,vol.125,pp.125−133,Feb.2014.

[43]C.Mu,Z.Ni,C.Sun,and H.He,“Air-Breathing Hypersonic Vehicle Tracking Control Based on Adaptive Dynamic Programming,”IEEE Transactions on Neural Networks&Learning Systems,vol.28,no.3,pp.584−598,Mar.2017.

[44]Q.Wei and D.Liu,“Data-driven neuro-optimal temperature control of water-gas shift reaction using stable iterative adaptive dynamic programming,”IEEE Transactions on Industrial Electronics,vol.61,vol.11,pp.6399−6408,Nov.2014.

[45]Y.Xu,D.Liu,and Q.Wei,“Action dependent heuristic dynamic programming based residential energy scheduling with home energy interexchange,”Energy Conversion and Management,vol.103,pp.553−561,Oct.2015.

[46]Weather Underground,http://www.wunderground.com,available online Oct.2015.

[47]C.Chen,S.Duan,T.Cai,and B.Liu,“Online 24-h solar power forecasting based on weather type classification using artificial neural network,”Solar Energy,vol.85,no.11,pp.2856−2870,Nov.2011.

[48]C.Tao,S.Duan,and C.Chen,“Forecasting power output for gridconnected photovoltaic power system without using solar radiation measurement,”inProceedings of 2nd IEEE International Symposium on Power Electronics for Distributed Generation Systems,Hefei,China,Jun.2010,pp.773−777.

[49]P.Bacher,H.Madsen,and H.A.Nielsen,“Online short-term solar power forecasting,”Solar Energy,vol.83,no.10,pp.1772−1783,Oct.2009.

[50]ComEd,http://hourlypricing.comed.com,available online May 2017.

[51]OpenEI,http://en.openei.org/community,available online Aug.2014.

[52]T.Yau,L.N.Walker,H.L.Gupta,and A.Gupta,“Effects of battery storage devices on power system dispatch,”IEEE Transactions on Power Apparatus and Systems,vol.PAS-100,no.1,pp.375−383,Jan.1981.

[53]F.Wang,H.Zhang,and D.Liu,“Adaptive dynamic programming:an introduction,”IEEE Computational Intelligence Magazine,vol.4,no.2,pp.39−47,May 2009.

[54]R.E.Bellman,Dynamic Programmming.Princeton,NJ:Princeton University Press,1957.

[55]M.R.AlRashidi and M.E.El-Hawary,“A survey of particle swarm optimization applications in electric power systems,”IEEE Transactions on Evolutionary Computation,vol.13,no.4,pp.913−918,Aug.2009.