Feature Selection for Multi-label Classification Using Neighborhood Preservation

Zhiling Caiand William Zhu

I.INTRODUCTION

I N traditional single-label learning in data mining and machine learning,each instance is associated with a single label from a set of labels.However,in many real-world applications,one instance is usually associated with more than one label.For example,in scene classification[1],[2],an input image may be associated with a set of semantic classes,such as beach and sea.In text categorization[3],[4],a news document may cover several predefined topics simultaneously,such as government and health.In functional genomics[5],[6],a gene may belong to several functional classes simultaneously,such as transcription,protein synthesis and metabolism.From the above situation,the paradigm of multi-label learning naturally emerges with increasing attention.In artificial intelligence[7]−[10]and machine learning problems[11]−[13],high dimensionality often causes some negative effects includingcomputational burden and over-fitting.Therefore,dimensionality reduction is an important task but challenging issue in data mining and machine learning.It has been extensively studied in single-label learning.Dimensionality reduction in multi-label learning is thus more difficult because of more complex structures.As we know,only a few works address the problem of dimensionality reduction for multi-label learning.

The two main approaches to dimensionality reduction in multi-label learning are feature extraction and feature selection.The former aims to map the original features into a low dimensional space via a certain transformation and generates some new features[14]−[18],while the latter is to choose a subset of original features according to a certain criterion[19]−[22].Compared with feature extraction,feature selection can keep the original physical meanings of each feature.Consequently,feature selection has been a popular research topic.Feature selection techniques can be mainly categorized into three groups:w rapper,embedded and filter[23],[24].Wrapper approaches[25],[26]employ the predictive accuracy of a predetermined classifier algorithm to determine the goodness of selected features.Obviously,w rapper approaches often need more computational cost.Embedded approaches[27],[28]achieve feature selection and model construction simultaneously.Filter approaches[29]−[31]are viewed as one pure pre-processing tool,fully irrelevant to any classifier.This type of methods select the top ranked features before doing learning task by analyzing the intrinsic structure of the data.In this paper,we are much interested in filter approaches since they are usually more efficient than wrapper and embedded approaches.

To the best of our know ledge,most existing filter algorithms[32]−[36]transform the multi-label problems into traditional single-label problems.A popular strategy converts multiple labels into several binary single-labels,and then evaluates the relevance of each feature for each label independently using some score evaluation methods[31],[34],[37].Subsequently the obtained scores are combined in order to obtain a global feature ranking.The other popular strategy converts multiple labels into a single-label composed of multiple classes,and then solves the multi-class single-label feature selection problem[35],[38],[39].These transformation-based feature selection approaches can apply mature single-label techniques to multi-label problems.However,the complexity of new feature selection problems will increase sharply after problem transformation.To tackle this,some algorithm-adaptation feature selection approaches[40],[41]directly handle multilabel problems.The key step of these approaches is to design a certain effective feature evaluation criterion for multi-label problems.

In this paper,we propose an effective feature evaluation criterion,called neighborhood relationship preserving score(NRPS),for multi-label feature selection.NRPS is inspired by similarity preservation[42]which is widely used in singlelabel feature selection.Unlike in similarity preservation,we address the order of sample similarities which can well express the neighborhood relationship among samples,not just the pairwise sample similarity.We extend the formulation of similarity preservation using linear function of the sample similarity matrix based on feature subspace to approximate the sample similarity matrix based on label space.With linear approximating,the order of sample similarities is approximately preserved,which implies that samples with similar neighborhood relationship of label space are likely to have similar neighborhood relationship of feature subspace.First,we construct the formulation of neighborhood relationship preserving and then obtain NRPS to measure the importance of each feature subset.NRPS evaluates each feature subset by measuring its capability in preserving neighborhood relationship among samples.Second,two multi-label feature selection algorithms with NRPS are designed.One is based on ranking method which evaluates features individually,and the other is based on a greedy method.Finally,we compare the proposed algorithms with Baseline method and four multi-label state-of the-arts.Experimental results in six publicly available data sets demonstrate that the proposed algorithms outperform other algorithms inmost cases for all tested data sets.The overview of this paper can be represented as Fig.1.

The rest of this paper is arranged as follows.In Section II,we discuss some related works.In Section III,we propose a feature evaluation criterion based on preserving neighborhood relationship.In Section IV,we design two multi-label feature selection algorithms by this criterion.We report and analyze the experimental results in Section V.Finally,we conclude this paper in Section VI.

II.RELATED WORKS

In this section,we review some related works on multilabel classification problems and similarity preserving feature selection.

A.Multi-label Classification Problems

Early researches on multi-label learning mainly focus on the investigation of multi-label text categorization techniques[2].The generality of multi-label problems intuitively makes learning task more difficult to solve[43],[44].An intuitive strategy is to decompose the multi-label learning into a number of binary classification problems(one per label)and thus ignores the correlations between different labels[45].However,this strategy suffers from that the number of binary classifiers will be too large when there are a lot of class labels.It may also result in the problem of imbalanced class distribution.In order to overcome this problem,Zhang and Zhou proposed a multi-labelK-nearest neighbor learning algorithm named MLKNN[46].It employs the statistical information gained from each example’sknearest neighbors and utilizes maximum a posteriori(MAP)principle to determine the label set.Another simple yet effective multi-label learning method is named label power set(LP)[47].The basic idea of LP is to transform the multi-label data set into a single-label data set with the same set of labels.Label power set approach directly transforms the multi-label dataset into one single-label dataset in the training set in which any single-label learning method is available[48].Some multi-label learning algorithms transform the problem into ranking tasks,to evaluate the labels for each sample by certain criterion.Widely used ranking algorithms include Rank SVM[49]and BoosTexter[3].Some other multi-label learning algorithms try to employ the correlation between different class labels.These methods include algorithms based on probabilistic generative models[50]and maximum entropy methods[51].Recently,Houet al.[52]proposed a novel multi-label learning method by exploring the manifold in the label space.This method assumes that the local topological structure can be shared between the feature manifold and the label manifold.

B.Similarity Preserving Feature Selection

Different feature evaluation criteria have been developed to evaluate the goodness of features.Reference[42]reviewed a number of existing feature evaluation criteria that selected features via preserving sample similarity,such as Laplacian score,Fisher score and ReliefF.Laplacian score[53]was to select features by retaining sample locality.Fisher score[54]was to select features that assigned different values to samples from different classes and similar values to samples from the same class.ReliefF[55]suggested that the algorithm selects features that contribute to the separation of samples from different classes.All criteria reviewed above can be unified under the following framework:

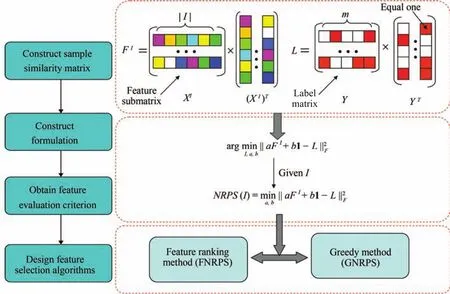
Fig.1.Overview.

III.MULTI-LABEL FEATURE EVALUATION CRITERION BASED ON NEIGHBORHOOD RELATIONSHIP PRESERVING

From viewpoint of the feature selection,we propose a feature evaluation criterion to measure the importance of each feature subset.The proposed criterion can be used to select an optimal subset of features from the original feature space by certain strategies including feature ranking and greedy search.

In this paper,we useX=Rdto denote thed-dimensional feature space andC={c1,...,cm}to denote the label set.LetD={xi,Yi|1≤i≤n}denote a multi-label training set withninstances,wherexi∈Xis ad-dimensional feature vector[xi1,...,xid]andYi⊆Cis the label set associated withxi.The subsetYican also be described as amdimensional binary vectoryi=[yi1,...,yim]whereyij=1 ifYihas labelcjand 0 otherwise.

The generic problem of feature selection is to select a feature subset to approximately represent all features.DenoteI⊆{1,...,d}as the index set of the selected features.An instancex∈Rdcan be approximately represented asx I∈R|I|after feature selection,wherexIis the sub-vector ofx.According to training setDand index setI,we construct two sample similarity matrices,one based on feature subspace and the other based on label space.Fowe define sample similarity matrix based on feature subspace asF I=For{y1,...,yn},we define sample similarity matrix based on label space asL=[Lij]n×n,Lij=〈yi,yj〉.If a pair of samples contains more same labels,they could be considered to be more similar.Inspired by the framework of[42],a formulation to capture the idea of similarity preservation can be constructed as follows:

It assumes that the similarity of each paired samples in subspace approximately equals to that in label space.However,the two kinds of similarities are more likely to have different scales between them.In other perspective,we can consider the order of sample similarities in each kind of space.In each sample similarity matrix,the bigger the similarity of a paired samples is,the closer the paired samples are.Therefore,the order of sample similarities can well express neighborhood relationship among samples.We extend the formulation using linear function of the sample similarity matrix based on feature subspace to approximate the sample similarity matrix based on label space.With linear approximating,the order of sample similarities is approximately preserved,which implies that samples with similar neighborhood relationship of label space are likely to have similar neighborhood relationship of feature subspace.From above analysis,we construct a formulation of neighborhood relationship preserving as follows:

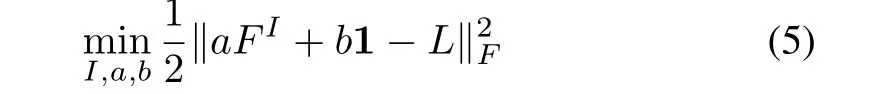
whereaandbare two variables to be solved and1∈Rn×ndenotes the matrix whose all elements are1.

To get a feature evaluation criterion from this formulation,we assume thatIis known.Then,we obtain

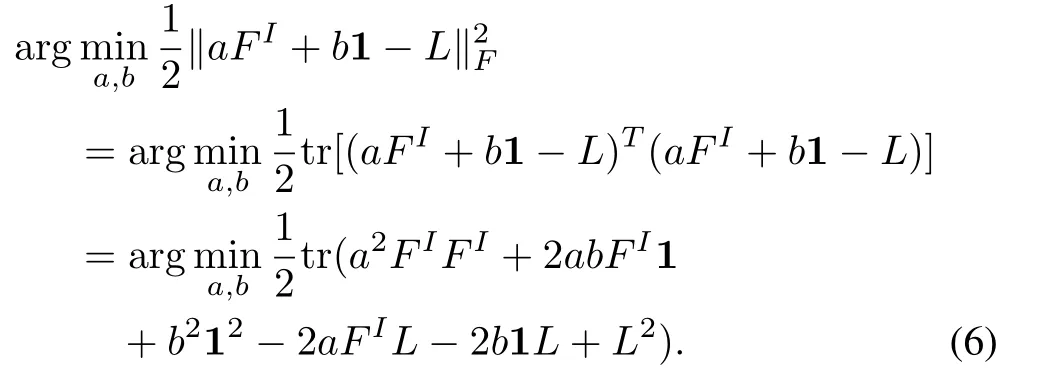
By setting its derivative with respect withbto zero,we have

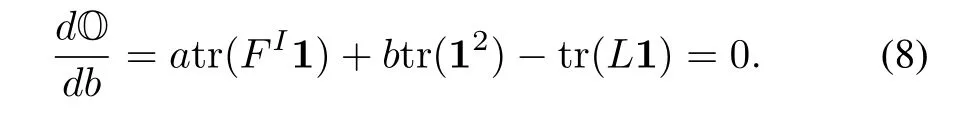
Based on(7)and(8),we have

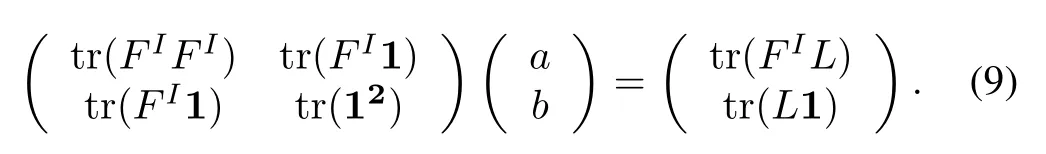
To obtain the solution of(9),Lemma 1 and corresponding corollary 1 are introduced.

Lemma 1:Cauchy’s inequality[56]:Supposeα1,...,αn,β1,...,βn∈R,then

where the equality sign holds if and only ifβi=0 orαi=cβi(i=1,...,nandc∈R).

Corollary 1:IfAandBare both symmetric matrices,then

where the equality sign holds if and only ifB=0orA=cB(c∈R).

Obviously,the similarities among samples are not all the same in real applications.Therefore,we obtainF I/=c1(c∈R),then we have

Hence,we have

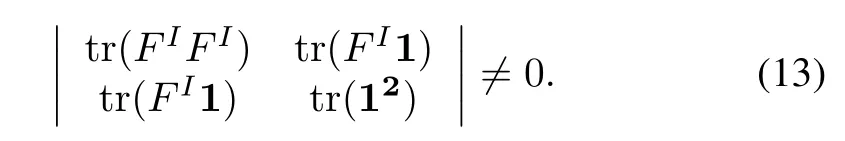
Based on(9)and(13),we can obtain a unique solution ofaandb:

Then,we easily get a feature evaluation criterion,called neighborhood relationship preserving score(NRPS),to evaluate the importance of each feature subset.For each index setI,we compute the NRPS of the feature subset corresponding to index setIas follows:

The smaller the value is,the more important the feature subset.

IV.OPTIMIZATION AND ALGORITHM

The feature evaluation criterion NRPS in fact evaluates each feature subset by measuring its capability in preserving neighborhood relationship among samples.With NRPS,we design two multi-label feature selection algorithms,one based on feature ranking method and the other based on a greedy method.

A.Feature Ranking Method for Multi-label Feature Selection

Algorithm 1.Feature ranking algorithm based on neighborhood relationship preserving score(FNRPS)

B.Greedy Method for Multi-label Feature Selection

In this subsection,drawing from that NRPS can be applied to measure the importance of each feature subset,a greedy algorithm for feature selection is designed.Here,we use a traditional forward search strategy to select features.First,we initialize the index set of selected featuresIasφand the index set of featuresDas{1,...,d}.Second,we put the elements ofDintoIone by one based on the following function:

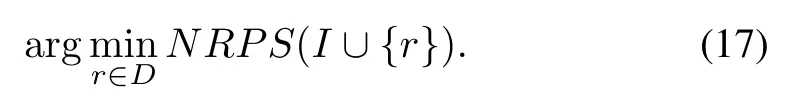
This algorithm considers the dependency between the candidate feature and selected features.Its pseudo-code is shown in Algorithm 2.To selectkfeatures,GNRPS needs to runkiterations.According to Algorithm 1,it is easy to show that the computational complexity of Algorithm 2 isO(kdn2).

Algorithm 2.Greedy algorithm based on neighborhood relationship preserving score(GNRPS)

Output:An index set of the selected features I⊆{1,...,d}and|I|=k.1:Compute similaritymatrix based on labelspace L,L=YYT;2:I=Ø,D={1,...,d},F I=0;//Initialize I,D,F I 3:X=XG−1,where G=p diag(X T X);//Normalize X 4:Cn=In−11T/n;//Compute centering matrix 5:X=Cn X;//Zero mean regularization 6:repeat 7: for r∈D do 8: Computing F r,where F r=F I+F{r};9: a= tr(F r L)tr(1 1)−tr(F r 1)tr(L 1)tr(F r F r)tr(1 1)−tr(F r 1)tr(F r 1);10: b=tr(F r F r)tr(L 1)−tr(F r 1)tr(F r L)t r(F r F r)t r(1 1)−t r(F r 1)t r(F r 1);11: SC(r)= ‖aF r+b1−L‖2F;12: end for 13: I←I∪{r∗},D←D−{r∗},F I←F r∗,where r∗=argm inr SC(r);14:until|I|=k 15:return feature index set I.

V.EXPERIMENT AND ANALYSIS

In this section,we conduct extensive experiments to evaluate to evaluate the performance of the two proposed algorithms,which can be applied to multi-label classification.We select classification algorithm ML-KNN[46]as the classifier for evaluation.

A.Evaluation Metric

Performance evaluation of multi-label learning systems is different from single-label systems.Multi-label learning systems require much more complicated evaluation measures.For the definitions of these measures we will consider a test data setS={(xi,Yi)|1≤i≤p}.Given an instancexi,the set of labels that is predicted by a multi-label classifier is denoted ash(xi),while the rank predicted for a labelyis denoted asranki(y).The following multi-label evaluation measures proposed in[3]are employed.

1)Average Precision(AP):

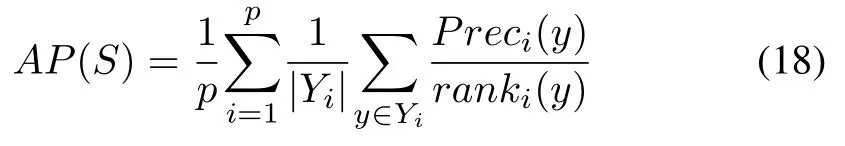
wherePreci(y)=|{y′|ranki(y′)≤ranki(y),y′∈Yi}|.This measure evaluates the average fraction of labels ranked above a particular label in the ground-truth label set.The bigger the value is,the better the performance is.

2)Coverage(CV):

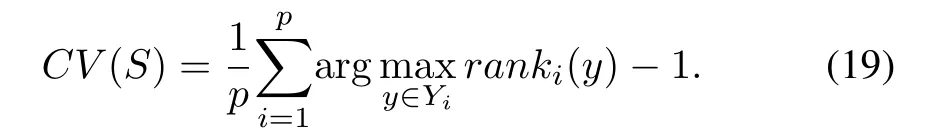
This measure evaluates how many steps we need,on the average,to go down the list of labels in order to cover all the ground-truth labels of the instance.The smaller the value is,the better the performance is.

3)Hamming Loss(HL):

where⊗stands for the symmetric difference of two sets.This measure evaluates the fraction of misclassified instance-label pairs.That is to say,a label belonging to the instance is not predicted or a label not belonging to the instance is predicted.The smaller the value is,the better the performance is.

4)One-error(OE):

whereδ(ξ)is the indicator function which for any predicateξ,δ(ξ)equals 1 ifξholds and 0 otherwise.This measure evaluates how many times the top-ranked label is not in the relevant label set.The smaller the value is,the better the performance is.

5)Ranking Loss(RL):

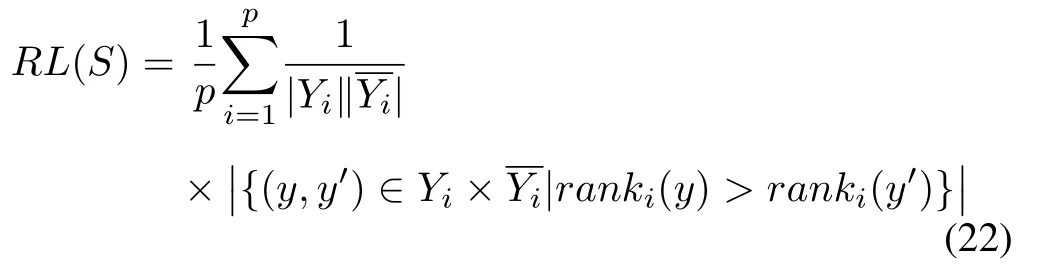
wheredenotes the complementary set ofYiwith respect toC.This measure evaluates the average fraction of label pairs that irrelevant label are ranked higher than relevant label.The smaller the value is,the better the performance is.

B.Datasets

In our experiments,we experiment with six real-world data sets including Business,Computers,Science,Reference,Arts and Yeast from various application scenarios.Business,Computers,Science,Reference and Arts are widely applied to automatic web page categorization.Each document is described as a feature vector using the “Bag-of-words”representation[57].For each data set,the training set contains 2000 documents while the test set contains 3000 documents.Yeast is created to address the problem of gene function classification of the Yeast saccharomyces cerevisiae.Each gene is described by the concatenation of micro-array expression data and the gene functional classes made from the hierarchies that represent maximum 190 functions[49].The original set contain a training set and a test set which have 1500 objects and 917 objects,respectively.Above selected data sets are all from Mulan Library1http://mulan.sourceforge.net/datasets-mlc.html.Given a multi-label data setD={(xi,Yi)|1≤i≤p},we usedim(D),L(D),|D|to represent the number of features,number of total labels,and number of instances,respectively.The detailed information of these datasets is described in Table I.Besides,two multi-label statistics[58]are also shown as follows:

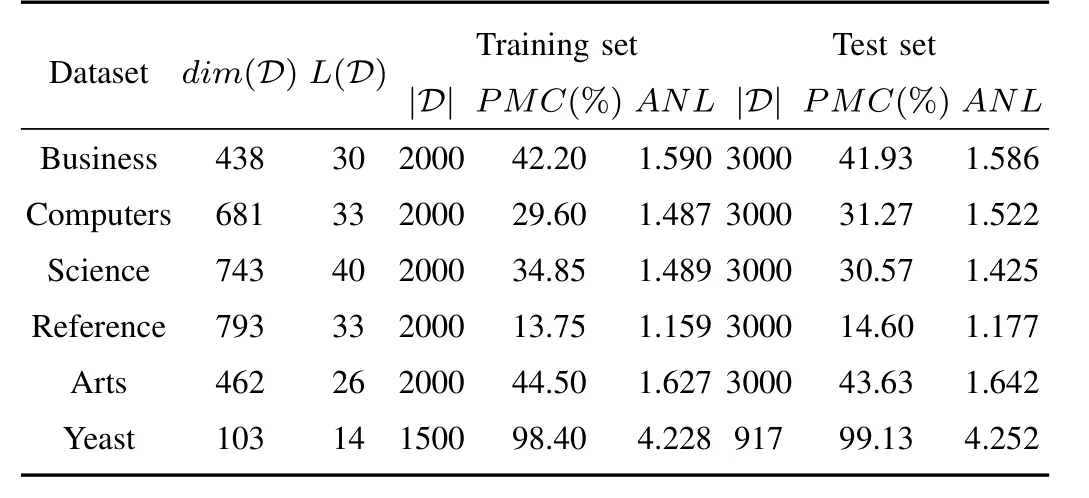
TABLE I DATA DESCRIPTION

C.Experimental Setting

In this subsection,we empirically evaluate the performance of the proposed algorithms in multi-label learning context.To demonstrate the efficiency of the algorithms,we compare the two proposed algorithms FNRPS and GNRPS with baseline method and four state-of-the-art multi-label feature selection methods:LP+RF[33](we represent this method as problem transformation+score function),PMU[40],MDMR[59]and FIMF[41].Note that LP+RF,FIMF and FNRPS select feature subset by feature ranking process and PMU,MDMR and GNRPS select feature subset by heuristic process.Different from PMU,FIMF and MDMR,our proposed algorithms share the geometry structure between the feature space and label space,which has been widely used in single-label learning.Brief description of each compared method is given below.

1)Baseline represents the method that all original features are selected for learning task.

2)LP+RF firstly transforms multi-label problem into single-label problem.Then transformed labels are given to ReliefF for obtaining the importance of each original feature.The evaluation criterion of ReliefF suggests that the algorithm selects features contributing to the separation of samples from different classes.

3)PMU proposes a mutual information based multi-label feature selection criterion.It selects an effective feature subset by maximizing the dependency between selected features and labels.

4)MDMR selects superior feature subset by an evaluation measure that combines mutual information with a maxdependency and min-redundancy.

5)FIMF proposes a fast multi-label feature selection method based on information-theoretic feature ranking.It derives a score function based on information theory for assessing the importance of each feature.

The two proposed algorithms are compared with the above existing state-of-the-art feature selection algorithms,where ML-KNN is selected as the base classifier for evaluation.Moreover,the number of nearest neighborsKand the value of smoothSare set as10 and 1 for ML-KNN,respectively.In this paper,we evaluate the performance of the above different feature selection methods by considering their average precision,coverage,hamming loss,one-error and ranking loss.These evaluation measures evaluate the performance of multi-label learning systems from different aspects.For PMU,MDMR and FIMF,we discretize the data sets using the equal-width interval,i.e.,default setting in their paper.For FIMF,we setQ=10,b=2 and all high-entropy features are remained.We run experiments with the number of selected features ranging from 5%to 40%of the dimension of all features,with 5%as an interval.

D.Experimental Results

Comparing with several multi-label feature selection algorithms,including LP+RF,PMU,MDMR and FIMF,we test the performance of the two proposed algorithms in terms of classification.For the parameter settings,Tables II−VI report the best results of all feature selection algorithms on average precision,coverage,hamming loss,one-error and ranking loss,respectively.In these tables,we use bold font to represent the best performance and underline to represent the second best performance.All experimental results in these tables indicate that the proposed algorithms,including FNRPS and GNRPS,outperform the compared existing algorithms inmost cases for all tested data sets.In particular,FNRPS totally outperforms compared algorithms for Business,Science and Arts data sets;GNRPS totally outperforms compared algorithms for Science,Reference,Arts and Yeast data sets.Furthermore,from the average results,we can conclude that GNRPS is superior to FNRPS,since GNRPS considers the dependence among features.

In order to demonstrate the experimental results in more detail,Figs.2−6 report the average precision,coverage,hamming loss,one-error and ranking loss performance,respectively,according to the number of input features.In thesefigures,the horizonal axis represents the number of input features selected by each feature selection algorithm,and the vertical axis indicates the corresponding classification performance of evaluation metric.From these figures,we have the following observations.First,feature selection not only reduces the number of features and shortens the running time of classifiers,but also improves the performance of classification by removing the redundant and/or irrelevant features.Second,FNRPS and GNRPS come with better performance than compared algorithms in most cases for all tested data sets.Especially,both FNRPS and GNRPS have very superior performance in hamming loss cases.Third,the performance of FNRPS is little poor in reference and yeast data sets,but it is also comparable to compared algorithms in these two data sets.Furthermore,GNRPS overcomes other algorithms in almost all cases for yeast data set.Therefore,we can conclude that FNRPS and GNRPS are superior to previous algorithms.

TABLE II AVERAGE PRECISION OF DIFFERENT ALGORITHMS WHEN ML-KNN IS USED AS A BASE CLASSIFIER

TABLE III COVERAGE OF DIFFERENT ALGORITHMS WHEN ML-KNN IS USED AS A BASE CLASSIFIER

Fig.2.Average precision of different feature selection methods when ML-KNN is used as a base classifier(the bigger the better).

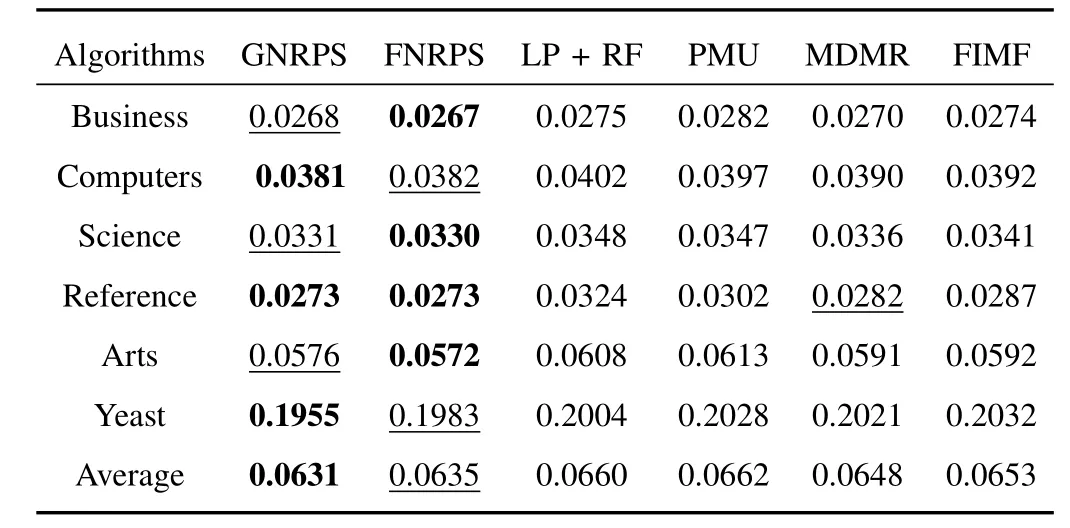
TABLE IV HAMMING LOSS OF DIFFERENT ALGORITHMS WHEN ML-KNN IS USED AS A BASE CLASSIFIER

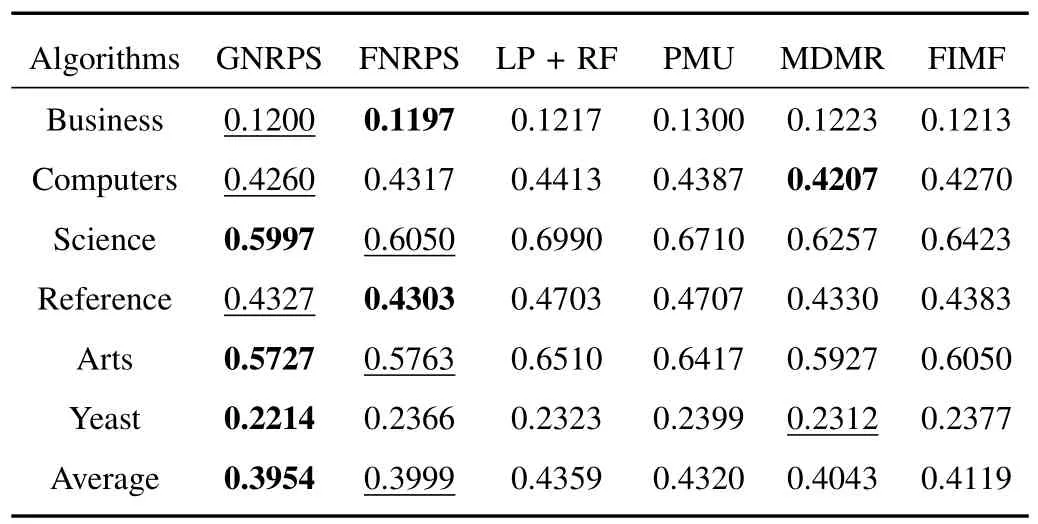
TABLE V ONE-ERROR OF DIFFERENT ALGORITHMS WHEN ML-KNN IS USED AS A BASE CLASSIFIER

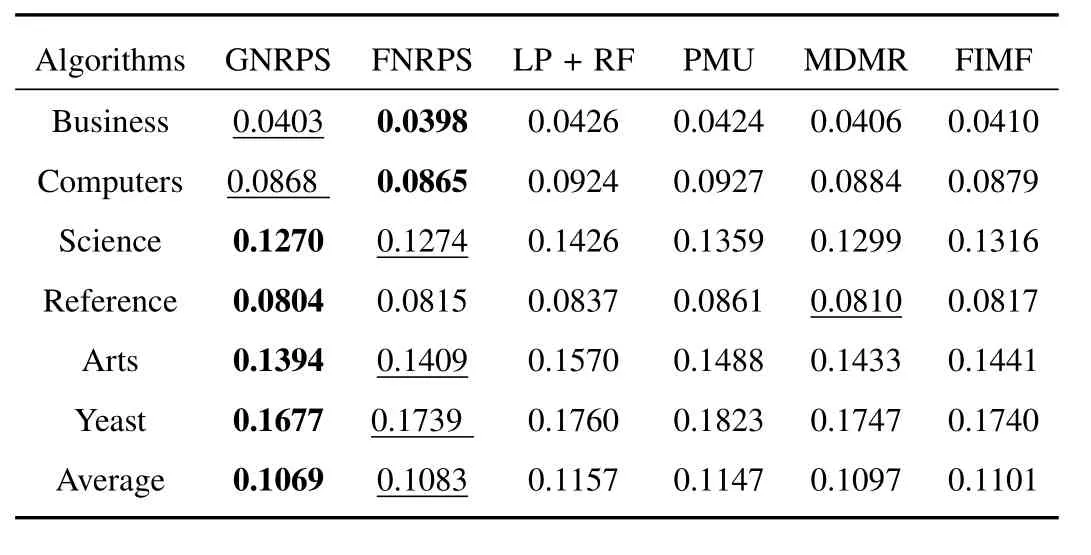
TABLE VI RANKING LOSS OF DIFFERENT ALGORITHMS WHEN ML-KNN IS USED AS A BASE CLASSIFIER

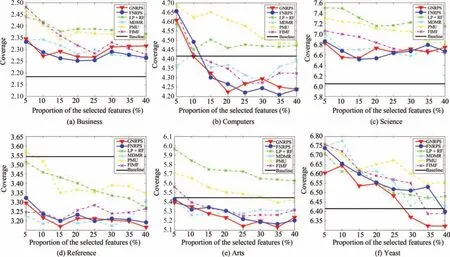
Fig.3.Coverage of different feature selection methods when ML-KNN is used as a base classifier(the smaller the better).

Fig.4.Hamming loss of different feature selection methods when ML-KNN is used as a base classifier(the smaller the better).

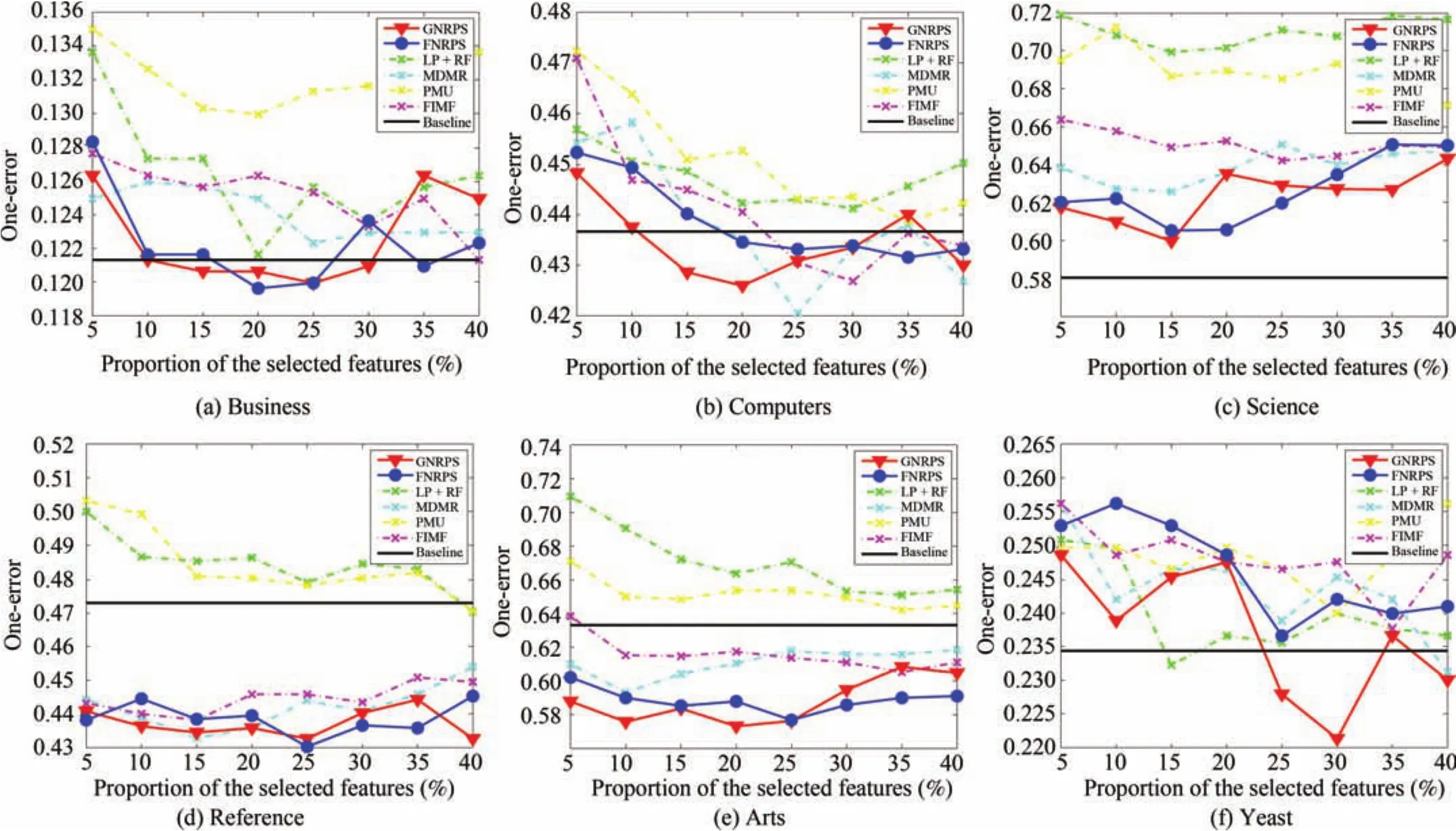
Fig.5.One-error of different feature selection methods when ML-KNN is used as a base classifier(the smaller the better).

Fig.6.Ranking loss of different feature selection methods when ML-KNN is used as a base classifier(the smaller the better).

VI.CONCLUSION

In this work,we study the problem of multi-label feature selection from the perspective of neighborhood relationship preserving,which is inspired by similarity preservation.To improve the formulation of similarity preservation,we use linear function of the sample similarity matrix based on feature subspace to approximate the sample similarity matrix based on label space.With linear approximation,the order of sample similarities is approximately preserved,which implies that samples with similar neighborhood relationship of label space are likely to have similar neighborhood relationship of feature subspace.By this formulation,we obtain an effective feature evaluation criterion to measure the importance of each feature subset.With the obtained criterion,two feature selection algorithms are designed for multi-label problems.The proposed algorithms select features which not only depend on sample label information,but also capture the geometry structure of the data.Experimental results in six publicly available data sets from two application areas demonstrate that the proposed algorithms are superior to previous algorithms.

In our current implementation,we only use a simple linear kernel to construct the sample similarity matrix.We will try to extend the current approach for general nonlinear kernels in our future research.

[1]M.R.Boutell,J.B.Luo,X.P.Shen,and C.M.Brown,“Learning multi-label scene classification,”Pattern Recognit.,vol.37,no.9,pp.1757−1771,Sep.2004.

[2]M.L.Zhang and Z.H.Zhou,“A review on multi-label learning algorithms,”IEEE Trans.Know l.Data Eng.,vol.26,no.8,pp.1819−1837,Aug.2014.

[3]R.E.Schapire and Y.Singer,“Boostexter:a boosting-based system for text categorization,”Mach.Learn.,vol.39,no.2−3,pp.135−168,May 2000.

[4]M.L.Zhang and L.Wu,“Lift:Multi-label learning with label-specific features,”IEEE Trans.Pattern Anal.Mach.Intell.,vol.37,no.1,107−120,Jan.2015.

[5]Z.Barutcuoglu,R.E.Schapire,and O.G.Troyanskaya,“Hierarchical multi-label prediction of gene function,”Bioinformatics,vol.22,no.7,pp.830−836,Apr.2006.

[6]M.L.Zhang and Z.H.Zhou,“Multilabel neural networks with applications to functional genomics and text categorization,”IEEE Trans.Know l.Data Eng.,vol.18,no.10,pp.1338−1351,Oct.2006.

[7]W.Zhu and F.Y.Wang,“Reduction and axiomization of covering generalized rough sets,”Inf.Sci.,vol.152,pp.217−230,Jun.2003.

[8]W.Zhu,“Topological approaches to covering rough sets,”Inf.Sci.,vol.177,no.6,pp.1499−1508,Mar.2007.

[9]W.Zhu,“Relationship between generalized rough sets based on binary relation and covering,”Inf.Sci.,vol.179,no.3,pp.210−225,Jan.2009.

[10]W.Zhu,“Relationship among basic concepts in covering-based rough sets,”Inf.Sci.,vol.179,no.14,pp.2478−2486,Jun.2009.

[11]F.Y.Wang, “Control 5.0:from New ton to Merton in Popper’s cybersocial-physical spaces,”IEEE/CAA J.Autom.Sinica,vol.3,no.3,pp.233−234,Jul.2016.

[12]F.Y.Wang,X.Wang,L.X.Li,and L.Li,“Steps toward parallel intelligence,”IEEE/CAA J.Autom.Sinica,vol.3,no.4,pp.345−348,Oct.2016.

[13]F.Y.Wang,J.J.Zhang,X.H.Zheng,X.Wang,Y.Yuan,X.X.Dai,J.Zhang,and L.Q.Yang,“Where does Alphago go:from Church-Turing thesis to Alphago thesis and beyond,”IEEE/CAA J.Autom.Sinica,vol.3,no.2,pp.113−120,Apr.2016.

[14]Y.Zhang and Z.H.Zhou,“Multilabel dimensionality reduction via dependence maximization,”ACM Trans.Know l.Discov.Data,vol.4,no.3,Article ID:14,Oct.2010.

[15]K.Fukunaga,Introduction to Statistical Pattern Recognition.San Diego,CA,USA:Academic Press,2013.

[16]I.T.Jolliffe,Principal Component Analysis,2nd ed.New York,USA:Springer,2002.

[17]K.Yu,S.P.Yu,and V.Tresp,“Multi-label informed latent semantic indexing,”inProc.28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval,Salvador,Brazil,2005,pp.258−265.

[18]H.Wold,“Estimation of principal components and related models by iterative least squares,”inMultivariate Analysis,P.R.Krishnajah,Ed.New York,USA:Academic Press,1966,pp.350−352.

[19]X.J.Chang,F.P.Nie,Y.Yang,and H.Huang,“A convex formulation for semi-supervised multi-label feature selection,”inProc.28th AAAI Conference on Artificial Intelligence,Québec City,Québec,Canada,2014,pp.1171−1177.

[20]X.N.Kong and P.S.Yu,“GMLC:a multi-label feature selection framework for graph classification,”Know l.Inf.Syst.,vol.31,no.2,pp.281−305,May 2012.

[21]L.Song,A.Smola,A.Gretton,J.Bedo,and K.Borgwardt,“Feature selection via dependence maximization,”J.Mach.Learn.Res.,vol.13,no.1,pp.1393−1434,Jan.2012.

[22]Z.Zhao,X.F.He,D.Cai,L.J.Zhang,W.Ng,and Y.T.Zhuang,“Graph regularized feature selection with data reconstruction,”IEEE Trans.Know l.Data Eng.,vol.28,no.3,pp.689−700,Mar.2016.

[23]G.Tsoumakas,I.Katakis,and I.Vlahavas, “Mining multi-label data,”inData Mining and Know ledge Discovery Handbook,O.Maimon and L.Rokach,Eds.Boston,MA,USA:Springer,2009,pp.667−685.

[24]A.Chinnaswamy and R.Srinivasan,“Hybrid feature selection using correlation coefficient and particle swarm optimization on microarray gene expression data,”inInnovations in Bio-Inspired Computing and Applications,V.Snášel,A.Abraham,P.Krómer,M.Pant,and A.Muda,Eds.Cham,Germany:Springer,2016,pp.229−239.

[25]O.Gharroudi,H.Elghazel,and A.Aussem,“A comparison of multilabel feature selection methods using the random forest paradigm,”inAdvances in Artificial Intelligence,M.Sokolova and P.van Beek,Eds.Cham,Germany:Springer,2014,pp.95−106.

[26]M.L.Zhang,J.M.Peña,and V.Robles,“Feature selection for multilabel naive bayes classification,”Inf.Sci.,vol.179,no.19,pp.3218−3229,Sep.2009.

[27]Q.Q.Gu,Z.H.Li,and J.W.Han,“Correlated multi-label feature selection,”inProc.20th ACM International Conference on Information and Know ledge Management,Glasgow,Scotland,UK,2011,pp.1087−1096.

[28]F.P.Nie,H.Huang,X.Cai,and C.Ding,“Efficient and robust feature selection via ell2,1-norms minimization,”inProc.23rd International Conference on Neural Information Processing Systems,Vancouver,British Columbia,Canada,2010,pp.1813−1821.

[29]L.J.Zhang,Q.H.Hu,J.Duan,and X.X.Wang,“Multi-label feature selection with fuzzy rough sets,”inRough Sets and Know ledge Technology,D.M iao,W.Pedrycz,D.śle¸zak,G.Peters,Q.Hu,and R.Wang,Eds.Cham,Germany:Springer,2014,pp.121−128.

[30]S.W.Ji and J.P.Ye,“Linear dimensionality reduction for multi-label classification,”inProc.21st International Jont Conference on Artifical Intelligence,Pasadena,California,USA,2009,pp.1077−1082.

[31]Y.M.Yang and J.O.Pedersen,“A comparative study on feature selection in text categorization,”inProc.14th International Conference on Machine Learning,San Francisco,CA,USA,1997,pp.412−420.

[32]D.G.Kong,C.Ding,H.Huang,and H.F.Zhao,“Multi-label reliefF and F-statistic feature selections for image annotation,”in2012 IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Providence,RI,USA,2012,pp.2352−2359.

[33]N.Spolaˆor,E.A.Cherman,M.C.Monard,and H.D.Lee,“A comparison of multi-label feature selection methods using the problem transformation approach,”Electron.Notes Theor.Comput.Sci.,vol.292,pp.135−151,Mar.2013.

[34]K.Trohidis,G.Tsoumakas,G.Kalliris,and I.P.Vlahavas,“Multilabel classification of music into emotions,”inInternational Society for Music Information Retrieval,Eds.Philadelphia,Pennsylvania USA:M ITP,2008,pp.325−330.

[35]J.Read,“A pruned problem transformation method for multi-label classification,”inProc.2008 New Zealand Computer Science Research Student Conference(NZCSRS 2008),Eds.Christchurch,New Zealand,2008,pp.143−150.

[36]S.Diplaris,G.Tsoumakas,P.A.Mitkas,and I.Vlahavas,“Protein classification with multiple algorithms,”inAdvances in Informatics,P.Bozanis and E.N.Houstis,Eds.Berlin,Heidelberg,Germany:Springer,2005,pp.448−456.

[37]W.Z.Chen,J.Yan,B.Y.Zhang,Z.Chen,and Q.Yang,“Document transformation for multi-label feature selection in text categorization,”in7th IEEE International Conference on Data Mining,Omaha,NE,USA,2007,pp.451−456.

[38]G.Doquire and M.Verleysen,“Feature selection for multi-label classification problems,”inAdvances in Computational Intelligence,J.Cabestany,I.Rojas,and G.Joya,Eds.Berlin,Heidelberg,Germany:Springer,2011,pp.9−16.

[39]G.Doquire and M.Verleysen,“Mutual information-based feature selection for multilabel classification,”Neurocomputing,vol.122,pp.148−155,Dec.2013.

[40]J.Lee and D.W.Kim,“Feature selection for multi-label classification using multivariate mutual information,”Pattern Recognit.Lett.,vol.34,no.3,pp.349−357,Feb.2013.

[41]J.Lee and D.W.Kim,“Fast multi-label feature selection based on information-theoretic feature ranking,”Pattern Recognit.,vol.48,no.9,pp.2761−2771,Sep.2015.

[42]Z.Zhao,L.Wang,H.Liu,and J.P.Ye,“On similarity preserving feature selection,”IEEE Trans.Know l.Data Eng.,vol.25,no.3,pp.619−632,Mar.2013.

[43]C.Xu,T.L.Liu,D.C.Tao,and C.Xu,“Local rademacher complexity for multi-label learning,”IEEE Trans.Image Process.,vol.25,no.3,pp.1495−1507,Mar.2016.

[44]S.M.Tabatabaei,S.Dick,and W.Xu,“Toward non-intrusive load monitoring viamulti-label classification,”IEEE Trans.Smart Grid,vol.8,no.1,pp.26−40,Jan.2017.

[45]S.Godbole and S.Sarawagi,“Discriminative methods for multi-labeled classification,”inAdvances in Know ledge Discovery and Data Mining,H.Dai,R.Srikant,and C.Zhang,Eds.Berlin,Heidelberg,Germany:Springer,2004,pp.22−30.

[46]M.L.Zhang and Z.H.Zhou,“ML-KNN:A lazy learning approach to multi-label learning,”Pattern Recognit.,vol.40,no.7,pp.2038−2048,Jul.2007.

[47]G.Tsoumakas,I.Katakis,and I.V lahavas,“Randomk-labelsets for multilabel classification,”IEEE Trans.Know l.Data Eng.,vol.23,no.7,pp.1079−1089,Jul.2011.

[48]G.Tsoumakas and I.Katakis,“Multi-label classification:an overview,”Int.J.Data Warehous.Min.,vol.3,no.3,Article ID:1,Jul.2007.

[49]A.Elisseeff and J.Weston,“A kernel method for multi-labelled classification,”inProc.14th International Conference on Neural Information Processing Systems:Natural and Synthetic,Vancouver,British Columbia,Canada,2001,pp.681−687.

[50]N.Ueda and K.Saito,“Parametric mixture models for multi-labeled text,”inProc.15th International Conference on Neural Information Processing Systems,Cambridge,MA,USA,2002,pp.737−744.

[51]S.H.Zhu,X.Ji,W.Xu,and Y.H.Gong,“Multi-labelled classification using maximum entropy method,”inProc.28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval,Salvador,Brazil,2005,pp.274−281.

[52]P.Hou,X.Geng,and M.L.Zhang,“Multi-label manifold learning,”inProc.30th AAAI Conference on Artificial Intelligence,Phoenix,Arizona,USA,2016,pp.1680−1686.

[53]X.F.He,D.Cai,and P.Niyogi,“Laplacian score for feature selection,”inProc.18th International Conference on Neural Information Processing Systems,Vancouver,British Columbia,Canada,2005,pp.507−514.

[54]R.O.Duda,P.E.Hart,and D.G.Stork,Pattern classification.New York,USA:John Wiley&Sons,2001.

[55]K.Kira and L.A.Rendell,“A practical approach to feature selection,”inProc.9th International Workshop on Machine Learning,San Francisco,CA,USA,1992,pp.249−256.

[56]G.H.Hardy,J.E.Littlewood,and G.Pólya,Inequalities.London,UK:Cambridge University Press,1952.

[57]S.Dumais,J.Platt,D.Heckerman,and M.Sahami,“Inductive learning algorithms and representations for text categorization,”inProc.7th International Conference on Information and Know ledge Management,Bethesda,Maryland,USA,1998,pp.148−155.

[58]J.Read,B.Pfahringer,G.Holmes,and E.Frank,“Classifier chains for multi-label classification,”Mach.Learn.,vol.85,no.3,pp.333−359,Dec.2011.

[59]Y.J.Lin,Q.H.Hu,J.H.Liu,and J.Duan,“Multi-label feature selection based on max-dependency and m in-redundancy,”Neurocomputing,vol.168,pp.92−103,Nov.2015.