Polynomial Approach to Optimal One-wafer Cyclic Scheduling of Treelike Hybrid Multi-Cluster Tools via Petri Nets

Fajun Yang,NaiqiWu,,Yan Qiao,,and Rong Su,

NOMENCLATURE

I.INTRODUCTION

A cluster tool in wafer fabrication integrates a robot,two load locks,and a few process modules.It is called single or dual-arm cluster tool if its robot has one or two arms.Through the loadlocks,raw wafers are loaded into the system in a cassette-by-cassette way.They are processed by process modules in a pre-specified order at each step and finally return to the loadlock where it came from[1].

Multi-cluster tools are composed of several individual cluster tools connected by buffering modules(BM s)with a linear or treelike topology[2].It is called a treelike hybridK-cluster tool if it containsK(≥2)individual cluster tools including both single and dual-arm tools with a treelike topology as shown in Fig.1,where the red line represents the wafer processing route.

Fig.1.The illustration of a treelike hybrid 5-cluster tool.

Compared with the scheduling problem of complex industrial processes[3]–[8],it seems that scheduling a single cluster tool is simple.However,many factors make the scheduling problem of cluster tools very complicated.Thus,extensive research efforts have been made for effective operation of cluster tools[9]–[18].For a detailed review in this field,the readers can refer as to[19].They show that a cluster tool mostly operates under a steady state in a process or trans port bound region.In practice,the robot task time is much shorter than wafer processing time[20]such that it is process-bound.In such a case,for dual-arm tools,a swap strategy is effective[12],while for single-arm ones,a backward strategy is optimal[21],[22].

To schedule multi-cluster tools,Jevtic and Venkatesh[23]proposes a heuristic method.By ignoring the robot moving time,Dinget al.[24]find an optimal periodical schedule by using an event graph(a special class of Petri nets)combined with a network model.Yiet al.[25]give a decomposition method.By considering the robot moving time,Chanet al.[26],[27]propose a method with polynomial complexity to find an optimal cyclic schedule for both single-arm 2-cluster tools and a treelikeM-cluster tool.Generally,their method can successfully find a multi-wafer cyclic schedule,i.e.,more than one wafer is produced in each period[11].For a cluster photolithography tool with multi-robot that can process a few different wafers at the same time,[28]investigates how incremental scheduling,a technique based on prioritized planning,can be used to schedule the system.

Due to its easy implementation,a one-wafer cyclic one is most desired by practitioners if it achieves the same maximum throughput as a multi-wafer cyclic schedule does.A multicluster tool with its bottleneck individual tool being process bound is said to be process-dominant[29],[30].It is shown that,for a process-dominant single-arm multi-cluster tool with a linear topology,an optimal one-wafer cyclic schedule(O2CS)can be always found by an efficient method[29].The methods for finding an O2CS for process-dominant linear hybrid multi-cluster tools are given in[31],[32].The capacity of the buffers linking the individual cluster tools has effect on the productivity of a multi-cluster tool.Baiet al.[33]present a method to optimize the configuration of buffer capacity such that a one-wafer cyclic schedule with the lower bound of cycle time can be found for multi-cluster tools.

Scheduling a treelike hybrid multi-cluster tool is much more complex than a linear one and thus more challenging.Yanget al.[34]present the conditions under which a one-wafer cyclic schedule with the lower bound(LB)of cycle time(OSLB)exists for such a tool and an efficient algorithm to find it if existing.However,if the conditions are not met,it is open whether there is an O2CS(its cycle time must be longer than its LB)and how it can be found if so.To find an O2CS for treelike hybrid multi-cluster tool,it needs to coordinate the behavior of the multiple robots,which is very challenging.Based on the results from[34],this work aims to answer this problem for the first time.

Since optimal cycle time implies the maximal productivity,an O2CS should always be the priority for scheduling a multicluster tool.To schedule a multi-cluster tool is to allocate the finite resources to its process modules dynamically.Since a finite capacity Petri net(PN)is an effective tool for modeling resource allocation,we develop a PN model for such a tool based on the finite capacity PN.With the model,this work makes the following contribution:

1)It proves that there is always a one-wafer cyclic schedule for a treelike hybrid multi-cluster tool.

2)It develops computationally efficient algorithms to find an O2CS by simply setting the robot waiting time properly.

Next section presents the PN model for treelike hybrid multi-cluster tools.Section III uses the model to analyze the dynamic behavior of individual tools.Section IV presents the existence of a one-wafer cyclic schedule and a method to find an O2CS.Section V shows the applications of the proposed method by examples.Finally,Section VI concludes this paper.

II.PETRI NET MODELING

We make the same assumption as those in[26],[27]as given in the Supplementary File.Let Nn={1,2,...,n}andandRi,i∈NK,denote theith tool and its robot,respectively.C1with loadlocks in it is called the head one,Ci,i/=1,is called a leaf one if it connects one tool only,and it is a fork tool if it connects at least three adjacent tools.For example,given the tool in Fig.1,C3andC5are leaf ones;whileC2is fork one.LetL={i|Ciis a leaf tool}be the set of indices for the leaf tools.For easy presentation,the tools are numbered such that,for any two adjacent toolsCkandCi,k/∈Landi∈NK{1},withCk/Cibeing the upstream/downstream one,we havei＞k[27].However,kandiare not necessarily in a consecutive order as shown in Fig.1.

A BM connectingCkandCiis seen as the outgoing module forCkand incoming one numbered as Step 0 forCi.Letn[i]be the index for the last step inCi,i∈NK.Then,there aren[i]+1 steps inCiincluding outgoing and incoming modules.Letf[i]∈Nn[i]denote the number of outgoing modules inCi,i/∈L.Iff[i]＞1,Ciis a fork.LetSijdenote Stepj(except BM(s))inCiwithS10for the loadlocks inC1,andandwithdenote outgoing modules.Note thatandare not necessarily in a consecutive order.The incoming module forCiis denoted asSi0.In this way,then[i]+1 steps inCiare denoted asandrespectively.Note thatif it is Step 1 andif it is the last step.

Petri nets are a kind of effective tools for modeling,analysis,scheduling,and control for discrete event systems[4],[5],[35]–[38].This work extends the resource-oriented PN[37],[38]to model the system.It is defined as PN=(P,T,I,O,M,K),wherePandTare finite sets of places and transitions;IandOare the input and output functions;M(p)is a marking representing the number of tokens in placepwithM0(p)being the initial marking;andKis a capacity function.For the transition enabling and firing rules,readers can refer to[37],[38].

A.PN for Hybrid K-Cluster Tools

This work adopts the PN models developed in[32]and a brief introduction to them is presented for self-completeness.For convenience,a token and a wafer are often used without any difference.

For a single-arm or dual-armCi,i∈NK,transitionxij,j∈Ωn[i],modelsRi’s moving from Stepsjtoj+1(or Step 0 ifj=n[i])with a wafer,placesriandpijmodelRiandSij,j∈Ωn[i],respectively,withK(pij)=1.IfCiis a singlearm tool,K(ri)=1;otherwiseK(ri)=2.For a single-armCishown in Fig.2,qijwithK(qij)=1 modelsRi’s waiting for unloading a wafer frompij,j∈Ωn[i].dijandzijwithK(dij)=K(zij)=1model thatRiholds a wafer for moving from Stepsjtoj+1(or Step 0 ifj=n[i])and loading a wafer intopij,j∈Ωn[i],respectively.uijandtijmodel thatRiremoves a wafer frompijand drops a wafer intopij,j∈Ωn[i],respectively.yij,j∈Ωn[i]{0,1},modelsRi’s moving from Stepsj+2 toj(or ton[i]−1 ifj=0,or ton[i]ifj=1)without carrying a wafer.

Fig.2.A PN model for a single-arm tool Ci.

For a dual-armCishown in Fig.3,dijandzijwithK(dij)=K(zij)=1 model the state that a swap ends andRi’s waiting for unloading a wafer frompij,j∈Ωn[i],respectively.qijwithK(qij)=2models that both arms ofRihold a wafer and wait during the swap atpij,j∈Ωn[i].tijanduijmodelRi’s loading and unloading a wafer into and frompij,j∈Ωn[i],respectively.

For a BM connectingCkandCi,k/∈LwithCkbeing the upstream one,there are four different cases:1)both are dual-arm tools(D-D in short);2)Ckis a single-arm tool andCia dual-arm one(S-D);3)Ckis a dual-arm tool andCia single-arm one(D-S);and 4)both are single-arm tools(S-S).

A BM is treated as a step or theqth outgoing module denoted byforCkand Step 0 denoted asSi0forCi.It is modeled byandpi0forCkandCiwithandThe PN models for the four cases are shown in Fig.4.Taking the S-S case as an example,StepforCkis modeled byandtogether with arcsandStep 0 forCiis modeled byzi0,ti0,pi0,qi0,ui0,anddi0together with arcs(zi0,ti0),(ti0,pi0),(pi0,ui0),(qi0,ui0),and(ui0,di0)as shown in Fig.4(d).

Initial markingM0can be set by usingV-tokens representing virtual wafers to describe the startup transient process as given in[32].AtM0,for each adjacent pairCkandCi,we assume that the token inpi0enablesonly.

Fig.4.The PN model for the BM between Ck and Ci:(a)D-D,(b)S-D,(c)D-S,and(d)S-S.

In Fig.4,has two output transitionsandui0,leading to a conflict.To avoid such a conflict,we introduce colors into the model.

Definition 1:The color of transitiontiis defined asC(ti)={ci}.

By Definition 1,the colors forui0andareci0and,respectively.

Definition 2:If a token in an input placepoftienablesti,it has the same color ofti,i.e.,{ci}.

By Definition 2,a token enteringpi0by firinghas colorci0and enablesui0,while the token enteringpi0by firingti0has colorand thus enablessuch that the model is conflict-free.One more issue is that the model for a single-arm tool is deadlock-prone.A control policy defined in[32]is applied to avoid any such deadlock.

Definition 3[32]:In the PN model of a treelike hybridK-cluster tool,for a single-armatM,yij,j∈andis control-enabled ifis control-enabled ifti1has just fired,andis control-enabled ifhas just fired.

By this control policy,the model is made deadlock-free.Thereafter,we assume that the model is controlled by the policy specified in Definition 3.

B.Modeling Activity Time

Time is associated with both transitions and places in the model.As done in[20],the time for a robot to move from one step to another with or without carrying a wafer is identical,and so is the time for unloading/loading a wafer from/into a process module.By following[39],the activity time is modeled as summarized in Table I.Slightly abusing the notation we use the same symbols for both single and dual-arm cluster tools.

TABLE I TIME DURATION ASSOCIATED with TRANSITIONS AND PLACES FOR TOOL Ci.

III.TIMELINESS ANALYSIS OF INDIVIDUAL TOOLS

This section presents the temporal properties for individual tools.According to Wuet al.[39],for a single-arm toolCi,the time taken for a wafer at Stepj,j∈Nn[i],is

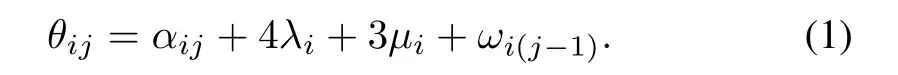
For Step 0,withαi0=0,we have

With robot waiting time being removed,(1)and(2)become

To be feasible,a wafer should stay inpijforτij(≥αij)time units.By replacingαijwithτij,the cycle time at Stepjis

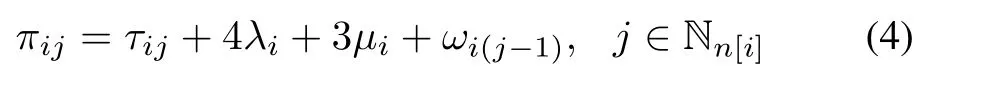
and

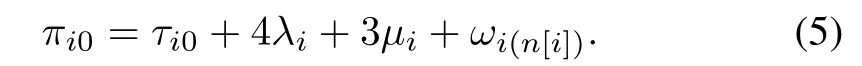
Its robot cycle time is

whereis the robot’s activity time in a cycle and is a constant,while∑ is the robot waiting time in a cycle.

For a dual-armCi,according to Wu and Zhou[1],we have the time needed for processing a wafer at Stepj,j∈Ωn[i]

Similarly,by replacingαijwithτijin(7),we have

Its robot cycle time is

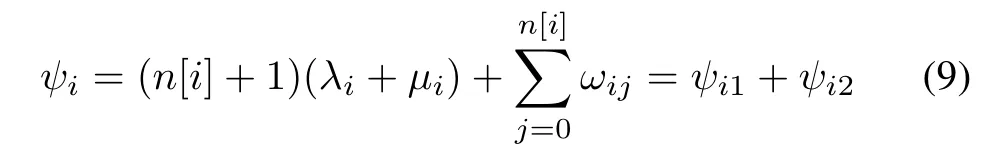
whereψi1andψi2have the same meaning as a single-arm tool.

For each toolCi,i∈NK,the productivity for each step is identical andCishould be scheduled such that

Since bothπiandψiare functions ofωij’s,the schedule for each toolCi,i∈NK,is parameterized by robots’waiting time.Hence,the key for scheduling a treelike hybridK-cluster tool is to determineωij’s such that the activities of the multiple robots are coordinated to act in a paced way.

IV.SCHEDULING THE OVERALL SYSTEM

A.Schedule Properties

LetΠi=m ax{ξi0,ξi1,...,ξi(n[i]),ψi1}denote the fundamental period(FP)ofCi,i∈NK.Further,letΠ=max{Π1,Π2,...,ΠK}=Πh,1≤h≤K,orChis the bottleneck tool.For a process-dominant treelike hybridK-cluster tool,Chmust be process-bound.LetΘbe cycle time for the system.Then,withπibeing the cycle time ofCi,to obtain a one-wafer cyclic schedule,each individual tool must have an identical cycle time,i.e.,

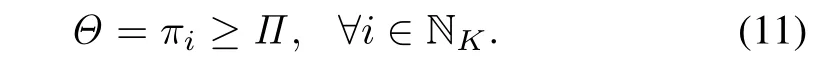
From[32],all the individual tools are scheduled to be paced,if and only if,for any adjacent pairCkandCi,k∈/Land,linked byat anyM,we have:1)wheneveris scheduled to load a token intopi0and 2)wheneverRi(Rk)is scheduled to unload a token fromIn[32],the existence of an OSLB is discussed and an algorithm is developed to find it if existing.For the case that there is no OSLB,this work answers how to find an O2CS with the minimum cycle timeΘ＞Π.

B.Optimal One-wafer Cyclic Scheduling

It has been proved in[31]that for the D-D and S-D cases,there is always a cyclic schedule for any adjacent pairCkandCisuch that their cycle time reaches the LB.Hence,for a process-dominant treelike hybridK-cluster tool,the conditions under which an OSLB exists are given as follows[34].

Lemma 1:For a process-dominant treelike hybridK-cluster tool,an OSLB exists,if and only if,for any adjacent pairCkandCi,k∈/Landconnected bythe following conditions are satisfied by determiningωkj’s andωil’s,j∈Ωn[k]andl∈Ωn[i]

IfCkandCiare D-S case

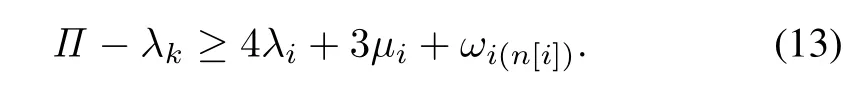
IfCkandCiare S-S case

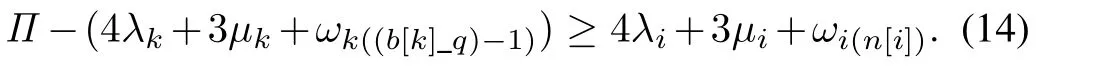
Based on Lemma1,an efficient method is developed in[32]to test the existence of an OSLB and find it if existing.Next,for such a system,we show that there is always a one-wafer cyclic schedule and present an efficient algorithm to find the minimal cycle timeΘand O2CS.Now we focus on the cases in which there is no OSLB.

LetBidenote a linear multi-cluster tool in a treelikeK-cluster tool called a branch that starts fromCiand ends atCm,m∈L.For easy presentation,the tools inBiare labeled consecutively asCi,Ci+1,...,andCm.Assume that,withΘ=Πas cycle time,the conditions given in Lemma 1 are violated for a pair ofCiandCi+1inBi.Letandj∈Ωn[k],whereωkjisRk’s waiting time obtained by the algorithm in[32]with cycle timeΘ=Π.LetwhenCiandCi+1are S-S;andwhenCiandCi+1are D-S.Ifit follows from[32]that an O2CS with cycle timeΘ=Π+Φi+1(S,S)(orΠ+Φi+1(D,S)ifCiis a dual-arm tool)can be found forBi.Otherw ise,ifassume that,forandorCg+1is a dual-arm one,org∈L.Defineandas the set of steps inCk,andThen,let[g]),and define Δi+1as follows.

ifCiis a single-arm tool,where Γ=B[i+1]+B[i+2]+···+B[g].

IfCiis a dual-arm one,Then,from[32],we have the following results.

Lemma 2[32]:ForBithat is composed of two tools,there is an O2CS and its minimal one-wafer cycle time isΘ=Π+Δ,where

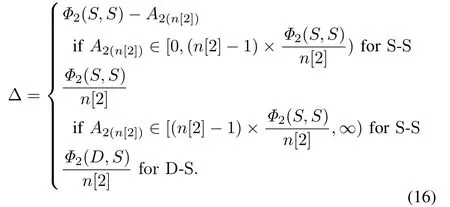
With Lemma 2,a method is proposed to find the minimal cycle time and O2CS forBiin[32].

Lemma 3[32]:ForBiin a treelike hybridK-cluster tool,if a one-wafer cyclic schedule with cycle timeΘ(≥Π)is found,a one-wafer cyclic schedule with cycle time(Θ+Δ)obtained by settingandis feasible.

Let STidenote a sub-tree in a tool that starts from a fork toolCi.Assume that STiand STjare two STs,and STiis contained by STj.Such a relation is denoted as STi＜STjor STj＞STi.The individual tools can be numbered such that STj＞STionly ifj＜i.However,j＜idoes not necessarily imply STj＞STi,for they may be independent of each other.Such a relation is denoted as STj∨STi.Next,we discuss the one-wafer cyclic scheduling problem and we have the following result.

Theorem 1:For an STicomposed of three tools,there is an O2CS and its minimal cycle time iswhere Δ1and Δ2are obtained in Lemma 2.

Proof:See the supplementary file.

The ST discussed in Theorem 1 represents the simplest case.A fork toolCiwithf[i]adjacent downstream tools...,andmay contain no ST but only branches denoted byBy the method in[32],one can find O2CSs forAssume that the cycle time for a branch composed ofCiandisΠ+Δq.Then,based on Theorem 1,we have the following corollary.

Corollary 1:For an STicomposed ofCiand its downstream branchesandthere is an O2CS and its minimal one-wafer cycle time iswhereΠ+Δqis the cycle time for the branch composed ofCiandB iq.

Then,an O2CS for a treelike hybridK-cluster tool can be found as follows.LetCjbe a fork tool.There must be its STj.Assume that there are toolsCi,Ci+1,...,Cj−2,andCj−1,with none being a fork tool.We call the multi-cluster tool formed byCi,Ci+1,...,Cj−2,Cj−1,and STjan extended sub-tree of STj,denoted as ESTi.The difference between STjand ESTiis thatCjin STjmust be a fork tool whileCiin ESTiis not a fork tool.Note that there may be more than one EST of STj.LetF={l|Clis a fork tool}be the set of indices for all fork tools.Letj=m axl∈F{l}.Then,STjmust contain no ST and its O2CS can be found based on Corollary 1.With an O2CS for STjfound,one needs to find O2CSs for all its ESTs.Then,letIffindh=maxl∈F{l}.If STh∨STj,it can be dealt with just as STj,otherwise,we have STh＞STj.In this case,we need to find an O2CS for SThand all its ESTs.Then,letand repeat the above process.In this way,we find O2CSs for all STs and their corresponding ESTs.WhenC1is reached,an O2CS for the whole system is obtained.Hence,the key is how to find an O2CS for an ST and its EST.By the definition of ESTk,ifin Corollary 1 is replaced bythe result must also hold.

Next,we first discuss how to find an O2CS for an EST that contains one fork tool only and then present a method to find an O2CS for the whole system.Assume thatj=m axl∈F{l}and ESTiis an extended sub-tree of STj.Furthermore,assume that,for tool pairCiandCi+1,i+1≤j,there is no one-wafer cyclic schedule with cycle timeΘ.Note that,with the O2CS for STjfound based on Corollary 1,Condition(13)or(14)is violated for pairCiandCi+1,i+1≤j,only.

Letandj∈Ωn[p],whereωpj’s are obtained by the algorithm in[32]with cycle timeΘ.DefineandandB[l]=n[l]−1,l∈NK.Letfor the S-S case andΦi+1(D,for the D-S case.It follows from[32]that,ifA(i+1)(n[i+1])=0,to make(13)or(14)satisfied forCiandCi+1,Θneeds to be increased byΦi+1(D,S)orΦi+1(S,S)time units.Ifwe need to check ifAj(n[j])=0.If so,we find the optimal cycle time via the methods in[32].Ifand there is a dual-arm tool in toolsCi+1,Ci+2,...,andCj,or there is at least oneAp(n[p])=0,i+1＜p＜j.In this case,to find the optimal cycle time,we need to examine toolsCi,Ci+1,...,andCponly.Since the system formed by these tools is a multi-cluster tool with linear topology,we can still find the optimal cycle time via the methods in[32].However,whenAp(n[p])＞0,i+1≤p≤j,we need to examine all the downstream tools ofCiand the problem is much more complicated.Hence,we cannot find the optimal cycle time by using the method in[32].We discuss how to find it next.

Assume thatCjhasf[j]downstream tools such that STjhasf[j]branches.Forinwe first check whetherIf so,findgsuch thatandis a dual-arm one,orLet

Then,we have the following result.

Theorem 2:Assume that:1)j=maxl∈F{l};2)for an ESTiof STj,by the algorithm in[32]with cycle timeΘ,Condition(14)is violated for pairCiandCi+1,i+1≤j,only;and 3)Δ=Δκ=Δi+1.Then,an O2CS with cycle timeΘ+Δ can be found for ESTi,where Δ is given by(17).

Proof:See the supplementary file.

By Theorem 2,with the cycle time being increased by Δ,it guarantees that whenRiis scheduled to unload a wafer fromhas just loaded a wafer there.Detailed explanation can be seen in the Supplementary File.IfCiandCi+1are D-S,we have the following result.

Theorem 3:Assume that:1)j=maxl∈F{l};2)for an ESTiof STj,by the algorithm in[32]with cycle timeΘ,Condition(13)is violated for pairCiandCi+1,i+1≤j,only;and 3)Δ=Δκ=Δi+1.Then,an O2CS with cycle timeΘ+Δ can be found for ESTi,where Δ is given by(17).Proof:See the supplementary file.

The idea of Theorem 3 can be similarly shown as that of Theorem 2 and its detail explanation can be seen in the Supplementary File.In Theorems2 and 3,we assume thatκ=i+1.Whenκ=arg1,q∈Nf[j]and 0≤z≤g,the following theorem presents how to find an O2CS for ESTi.

Theorem 4:Assume that:1)j=m axl∈F{l};2)in ESTiof STj,by the algorithm in[32]with cycle timeΘ,Condition(13)or(14)is violated for tool pairCiandCi+1,i+1≤j,only;and 3)Then,there is an O2CS with cycle timeΘ+Δ for ESTi,where Δ is defined in(17).

Proof:See the supplementary file.

By Theorems 2–4,to find an O2CS for an ESTiof STj,we requirejto be the largest one inF,and such an ESTicontains one fork tool only.This is not enough for one to find an O2CS for the entire system.However,based on Theorems 2–4,one can obtain an O2CS for arbitrary ESTkas follows.Assume that,for an ESTkthat contains more than one fork tool,Condition(13)or(14)is violated forCkandCionly,withCibeing the downstream adjacent tool ofCk.A path fromCkto a downstreamClis called a shortest path if the number of nodes(individual tools)on the path is minimal.Then,for an ESTk,we say thatClis “connected”toCkif:1)there are only single-arm tools on the shortest path fromCktoCl;and 2)for each toolCpon the path,0.Note thatCkis connected to itself.Letis connected toCk}.Furthermore,as done above,letΦi(S,for the S-S case andfor the DS case.Then,for any ESTkwithCibeing the downstream adjacent tool ofCk,to find the minimal one-wafer cycle time,we compute Δmas follows.

and ifm=i,it is calculated by(19),shown at the bottom of this page.

Clearly,(19)is the extension of(17).Thus,based on(18)and(19),we can find an O2CS for any ESTkif(13)or(14)is violated forCkandCionly.Then,the O2CS for an STjthat contains a number of ESTk’s can be obtained by using Corollary 1.We present the following algorithm.

Algorithm 1:Given an O2CS with cycle timeΘfor ESTi(or STi,orB i),find an O2CS for ESTk(or STk)withCibeing the downstream adjacent tool ofCk.

Step 1:Given cycle timeΘ,check ifΘis the optimal cycle time for ESTk(or STk)by the algorithm in[32].If yes,determine the schedule as in[32]and go to Step 5;

Step 2:Ifk/∈FandAi(n[i])=0,

(orΦi(D,S));

Step 2.2:Reset the robots’waiting time by the algorithm in[32]with cycle timeΘ,then go to Step 5.

Step 3:Ifk/∈Fand

Step 3.1:Form∈Si,calculate Δm’s via(18)or(19);

Step 3.2:If,do:

Step 3.2.1:If it belongs to the first case in(19),then

1)In ESTiorBi,forp∈/Si,ifp∈/L,otherwise

2)In ESTiorBi,ifp∈Siandp∈/F,set

3)In ESTi,ifp∈Siandp∈F,set

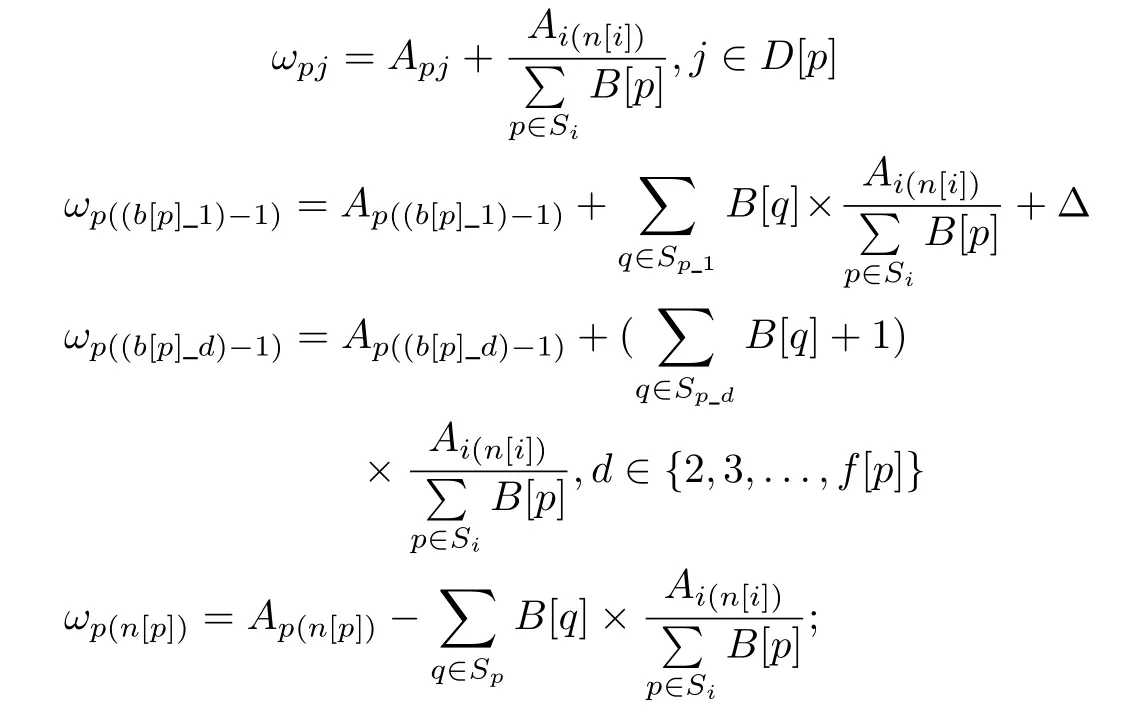
4)Go to Step 5.

Step 3.3:IfΔi,set the robot waiting time by repeating Procedures 1)–4)in Step 3.2.1 with bothand Δ =Φi(S,S)−A i(n[i])being replaced by Δ=Δf,then go back to Step 3.1.

Step 4:Ifk∈F,

Step 4.1:Find the optimal cycle timeΘ+Δqfor ESTkcomposed ofCkandNf[k],by repeating Steps 2 and 3;

Step 4.3:Find an O2CS for STkby resetting the robot waiting time with cycle timeΘby using the algorithm in[32].

Step 5:Output the schedule.

By Step 2 in Algorithm 1,ifk/∈FandAi(n[i])=0,it follows from[32]that,to make(13)or(14)satisfied,Θneeds to be increased byΦi+1(D,S)orΦi+1(S,S)time units.By Step 3,ifk∈/Fandwe calculate Δm’s,m∈Si,via(18)or(19).IfandCkandCiare S-S(or D-S)case,we obtain an O2CS for ESTkby setting the robot waiting time as Theorem 2(or 3)does.Otherwise,ifwe obtain an O2CS for ESTkby setting the robot waiting time as Theorem 4 does.By Step 4,ifk∈F,we find the optimal cycle time for ESTkcomposed ofCkandNf[k],by repeating Steps 2 and 3.Then,via Corollary 1,we haveAt last,by setting the robot waiting time with cycle timeΘvia the algorithm in[32],we obtain an O2CS for ESTk.

With the above analysis,an O2CS for a process-dominant treelike hybridK-cluster tool can be found as follows.We first find an O2CS for STjwithj=maxl∈F{l}and its ESTs.Then,letif,findh=maxl∈F{l}and an O2CS for SThand its ESTs.Continuing this process,an O2CS can be obtained for the entire system.However,by Algorithm 1,it requires that,for an ESTk,Condition(13)or(14)is violated for tool pairCkandCionly.This may not hold for general cases.To solve this problem,an O2CS for the ESTs of STjcan be found as follows.Based on the O2CS of STj,for ESTj−1withCj−1being not a fork,the above requirement must be satisfied.Thus,one can find an O2CS for ESTj−1by Algorithm 1.Then,one can do that for ESTj−2,till ESTisuch that the upstream adjacent tool ofCiis a fork.In this way,the above requirement is always satisfied.Thus,we present the following algorithm.

Algorithm 2:Find an O2CS for a process-dominant treelike hybridK-cluster tool.

Step 1:Θ =m ax{Π1,Π2,...,ΠK}andF={l|Clis a fork tool}.

Step 2:Check the existence of an OSLB by the algorithm in[32].

Step 2.1:If yes,determine the schedule as in[32]and go to Step 4;

Step 2.2:Otherwise find fork toolCjwithj=and go to Step 3.

Step 3:Find O2CSs for STjand all its ESTk’s.

Step 3.1:Find an O2CS for STj;

Step 3.2:Find O2CSs for all ESTk’s of STj

Step 3.2.1:Findksuch thatCkis the upstream adjacent

tool ofCj;

Step 3.2.2:IfCkis a fork tool,go to Step 3.3;other

w ise go to Step 3.2.3;

Step 3.2.3:Find an O2CS for ESTkby using

Algorithm 1;

ifi=1,go to Step 4;otherwise findksuch thatCkis the upstream adjacent tool ofCiand go to Step 3.2.2;

Step 3.3:Let,ifF/=∅,go back to Step 2.2.

Step 4:Output the schedule.

Notice that,for a treelike hybridK-cluster tool,the number of B’s,ST’s,and EST’s together must be less thanK.Also,any B or ST,or EST contains no more thanKtools.Given B,or ST,or EST,one needs to calculate the optimal cycle time at most(K−1)times by increasing Δ.Thus,the computational complexity of the proposed method isO(K2).WithKbeing limited in practice,the presented method is efficient and applicable to industrial cases.

V.ILLUSTRATIVE EXAMPLES

We use two examples to show the application of the proposed method.

Example 1:Consider a treelike hybrid 3-cluster tool,whereC1is a fork tool and its adjacent downstream tools areC2andC3.Among them,C2andC3are single-arm tools,andC1is a dual-arm one.Their activity time is as follows.ForC1,(α10,α11,α12,α13,λ1,µ1)=(0,77,0,0,23,1);forC2,(α20,α21,α22,λ2,µ2) = (0,75,79,4,1);and forC3,(α30,α31,α32,λ3,µ3)=(0,71,69,6,1).

ForC1,we haveξ10=23s,ξ11=100s,ξ12=23s,ξ13=23s,ψ11=(n[1]+1)×(λ1+µ1)=4×24=96s,andΠ1=100 s.ForC2,we haveξ20=19 s,ξ21=94 s,ξ22=98s,ψ21=2(n[2]+1)×(λ2+µ2)=6×5=30 s andΠ2=98 s.ForC3,we haveξ30=27s,ξ31=98 s,ξ32=96s,ψ31=2(n[3]+1)×(λ3+µ3)=6×7=42s andΠ3=98s.SinceΠ1=100＞Π2=Π3=98 andC1is process-bound,it is process-dominant and we letΘ=π1=π2=π3=Π=Π1=100 s.By the algorithm in[32],withΘ=100 s,the robots’waiting time is set asω20=6s,ω21=2s,andω22=Π−ψ21−ω20− ω21=100−30−6−2=62s;ω30=2s,ω31=4s,andω32=Π−ψ31−ω30−ω31=100−42−2−4=52s.Then,forC1,Π −(4λ2+3µ2+ω22)−λ1=100−(19+62)−23=−4＜0 andΠ−(4λ3+3µ3+ω32)−λ1=100−(27+52)−23=−2＜0,or(14)is violated and there is no OSLB.We need to find an O2CS.

By Algorithm 2,we have Δ2=Φ2(D,S)/n[2]=4/2=2 s,Δ3=Φ3(D,S)/n[3]=2/2=1 s,Δ =m ax{Δ2,Δ3}=2 s,and.Then,letandj∈Ωi(n[i]).By Algorithm 2,the robot waiting time is set asω30=A30+Δ =4 s,ω31=A31+Δ =6 s,ω32=A32−Δ =50s,ω20=A20+ Δ =8 s,ω21=A21+Δ=4s,ω22=A22−Δ=60 s,ω10=A10+Δ =6 s,andω11=ω12=ω13=0.In this way,an O2CS is obtained and its Gantt chart is shown in the Supplementary File.

Example 2:Consider a treelike hybrid 5-cluster tool withC2being a fork tool,and its adjacent downstream tools areC3andC5.C4andC2are downstream tools ofC3andC1,respectively.Among them,C1is a dual-arm tool and the others are single-arm ones.Their activity time is as follows:forC1,(α10,α11,λ1,µ1)=(0,61.5,0,28.5,0.5);forC2,(α20,α21,α22,λ2,µ2) = (0,0,0,10,1);forC3,(α30,α31,α32,α33,λ3,µ3)=(0,56,0,58,7,1);forC4,(α40,α41,α42,α43,λ4,µ4)=(0,56,66,65,5,1);and forC5,(α50,α51,α52,λ5,µ5)=(0,48,50,6,1).

It is found that the lower bound of cycle time isΘ=Π=90s.WithΘ=Π=90s,the robot waiting time is set as follows.ForC4,we haveω40=11s,ω41=1 s,ω42=2 s,andω43=28 s;forC5,ω50=15s,ω51=13s,andω52=20s;forC3,ω31=8s,ω30=3s,ω32=1s,andω33=14s;forC2,ω20=2s,ω21=0,andω22=22s.Then,forC1,Π−(4λ2+3µ2+ω22)−λ1=90−(43+22)−28.5=−3.5＜0,or there is no OSLB.Therefore,we need to find an O2CS.

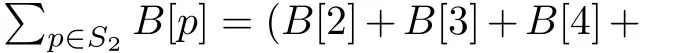
V I.CONCLUSIONS

Compared with linear multi-cluster tools,a treelike hybrid multi-cluster tool is topologically more complex.Optimal scheduling of such a multi-cluster tool requires that the activities of multiple robots for accessing the shared buffering modules should be properly coordinated.For a process-dominant treelike hybridK-cluster tool,our prior work[34]derives the conditions under which there is a one-wafer cyclic schedule that reaches the lower bound of cycle time and develops an algorithm to find it if existing.However,if these conditions are not satisfied,it is unknown whether there is an optimal one wafer cyclic schedule or not.Can we find it if existing?Aiming at answering these two questions,this work conducts a study based on the results obtained in[34].We have successfully shown that there is always a one-wafer cyclic schedule.We have also developed an efficient algorithm to find the minimal cycle time and the optimal one-wafer cyclic schedule.

For some wafer fabrication processes,there are strict wafer residency time constraints,and in some steps,there may have parallel modules.Meanwhile,in practice,the activity time may be subject to bounded variation.Dealing with them is our future work.

[1]N.Q.Wu and M.C.Zhou,“A closed-form solution for schedulability and optimal scheduling of dual-arm cluster tools with wafer residency time constraint based on steady schedule analysis,”IEEE Trans.Automat.Sci.Eng.,vol.7,no.2,pp.303−315,Apr.2010.

[2]W.K.Chan,J.G.Yi,and S.W.Ding,“On the optimality of one-unit cycle scheduling of multi-cluster tools with single-blade robots,”inProc.IEEE Int.Conf.Automation Science and Engineering,Scottsdale,AZ,USA,2007,pp.392−397.

[3]N.Q.Wu,L.P.Bai,and M.C.Zhou,“An efficient scheduling method for crudeoil operations in refinery with crudeoil typemixing requirements,”IEEE Trans.Syst.,Man,Cybern.Syst.,vol.46,no.3,pp.413−426,Mar.2016.

[4]N.Q.Wu,M.C.Zhou,L.P.Bai,and Z.W.Li,“Short-term scheduling of crude oil operations in refinery with high-fusion-point oil and two transportation pipelines,”Enterp.Inform.Syst.,vol.10,no.6,pp.581−610,Sep.2016.

[5]N.Q.Wu,M.C.Zhou,and Z.W.Li,“Short-term scheduling of crudeoil operations:Enhancement of crude-oil operations scheduling using a petrinet-based control-theoretic approach,”IEEE Robot.Automat.Mag.,vol.22,no.2,pp.64−76,Jun.2015.

[6]Y.Hou,N.Q.Wu,M.C.Zhou,and Z.W.Li,“Pareto-optimization for scheduling of crude oil operations in refinery via genetic algorithm,”IEEE Transactions on Systems,Man,Cybernetics:Systems,vol.47,no.3,pp.517−530,Mar.2017.

[7]S.W.Zhang,N.Q.Wu,Z.W.Li,T.Qu,and C.D.Li,“Petri net-based approach to short-term scheduling of crude oil operations with less tank requirement,”Information Sciences,vol.417,pp.247−261,Nov.2017.

[8]N.Q.Wu,Z.W.Li,and T.Qu,“Energy efficiency optimization in scheduling crude oil operations of refinery based on linear programming,”Journal of Cleaner Production,vol.166,49−57,Nov.2017.

[9]T.L.Perkinson,R.S.Gyurcsik,and P.K.M cLarty,“Single-wafer cluster tool performance:An analysis of the effects of redundant chambers and revisitation sequences on throughput,”IEEE Trans.Semicond.Manuf.,vol.9,no.3,pp.384−400,Aug.1996.

[10]T.L.Perkinson,P.K.McLarty,R.S.Gyurcsik,and R.K.Cavin III,“Single-wafer cluster tool performance:An analysis of throughput,”IEEE Trans.Semicond.Manuf.,vol.7,no.3,pp.369−373,Aug.1994.

[11]S.P.Sethi,C.Sriskandarajah,G.Sorger,J.Blazewicz,and W.Kubiak,“Sequencing of parts and robot moves in a robotic cell,”Int.J.Flex.Manuf.Syst.,vol.4,no.3−4,pp.331−358,Jun.1992.

[12]S.Venkatesh,R.Davenport,P.Foxhoven,and J.Nulman,“A steady state throughput analysis of cluster tools:Dual-blade versus single-blade robots,”IEEE Trans.Semicond.Manuf.,vol.10,no.4 pp.418−424,Nov.1997.

[13]N.Q.Wu,F.Chu,C.B.Chu,and M.C.Zhou,“Petri net modeling and cycle-time analysis of dual-arm cluster tools with wafer revisiting,”IEEE Trans.Syst.,Man,Cybern.Syst.,vol.43,no.1,pp.196−207,Jan.2013.

[14]N.Q.Wu and M.C.Zhou,“Modeling,analysis and control of dual-arm cluster tools with residency time constraint and activity time variation based on Petri nets,”IEEE Trans.Automat.Sci.Eng.,vol.9,no.2,pp.446−454,Apr.2012.

[15]N.Q.Wu and M.C.Zhou,“Schedulability analysis and optimal scheduling of dual-arm cluster tools with residency time constraint and activity time variation,”IEEE Trans.Automat.Sci.Eng.,vol.9,no.1,pp.203−209,Jan.2012.

[16]N.Q.Wu,M.C.Zhou,F.Chu,and C.B.Chu,“A Petri-net-based scheduling strategy for dual-arm cluster tools with wafer revisiting,”IEEE Trans.Syst.,Man,Cybern.Syst.,vol.43,no.5,pp.1182−1194,Sep.2013.

[17]F.J.Yang,N.Q.Wu,Y.Qiao,M.C.Zhou,and Z.W.Li,“Scheduling of single-arm cluster tools for an atomic layer deposition process with residency time constraints,”IEEE Trans.Syst.,Man,Cybern.Syst.,vol.47,no.3,pp.502−516,Mar.2017.

[18]W.M.Zuberek,“Timed Petri nets in modeling and analysis of cluster tools,”IEEE Trans.Robot.Automat.,vol.17,no.5,pp.562−575,Oct.2001.

[19]C.R.Pan,M.C.Zhou,Y.Qiao,and N.Q.Wu,“Scheduling cluster tools in semiconductor manufacturing:Recent advances and challenges,”IEEE Trans.Automat.Sci.Eng.,to be published.doi:10.1109/TASE.2016.2642997.

[20]J.H.Kim,T.E.Lee,H.Y.Lee,and D.B.Park,“Scheduling analysis of time-constrained dual-armed cluster tools,”IEEE Trans.Semicond.Manuf.,vol.16,no.3,pp.521−534,Aug.2003.

[21]T.E.Lee,H.Y.Lee,and Y.H.Shin,“Workload balancing and scheduling of a single-armed cluster tool,”inProc.5th APIEMS Conf.,Gold Coast,Australia,2004,pp.1−15.

[22]M.J.Lopez and S.C.Wood,“Systems of multiple cluster tools:Configuration,reliability,and performance,”IEEE Trans.Semicond.Manuf.,vol.16,no.2,pp.170−178,May 2003.

[23]D.Jevtic and S.Venkatesh,“Method and apparatus for scheduling wafer processing within a multiple chamber semiconductor wafer processing tool having a multiple blade robot,”U.S.Patent6 224 638,May 1,2001.

[24]S.W.Ding,J.G.Yi,and M.T.Zhang,“Multicluster tools scheduling:An integrated event graph and network model approach,”IEEE Trans.Semicond.Manuf.,vol.19,no.3,pp.339−351,Aug.2006.

[25]J.G.Yi,S.W.Ding,D.Z.Song,and M.T.Zhang,“Steady-state throughput and scheduling analysis of multicluster tools:A decomposition approach,”IEEE Trans.Automat.Sci.Eng.,vol.5,no.2,pp.321−336,Apr.2008.

[26]W.K.V.Chan,J.G.Yi,and S.W.Ding,“Optimal scheduling of multicluster tools with constant robot moving times,Part I:Two-cluster analysis,”IEEE Trans.Automat.Sci.Eng.,vol.8,no.1,pp.5−16,Jan.2011.

[27]W.K.V.Chan,S.W.Ding,J.G.Yi,and D.Z.Song,“Optimal scheduling of multicluster tools with constant robot moving times,Part II:Tree-like topology configurations,”IEEE Trans.Automat.Sci.Eng.,vol.8,no.1,pp.17−28,Jan.2011.

[28]S.Wareand R.Su,“An application of incremental scheduling to a cluster photolithography tool,”inIFAC World Congress2017,Toulouse,France,to be published.

[29]Q.H.Zhu,N.Q.Wu,Y.Qiao,and M.C.Zhou,“Petri net-based optimal one-wafer scheduling of single-arm multi-cluster tools in semiconductor manufacturing,”IEEE Trans.Semicond.Manuf.,vol.26,no.4,pp.578−591,Nov.2013.

[30]Q.H.Zhu,N.Q.Wu,Y.Qiao,and M.C.Zhou,“Scheduling of single-arm multi-cluster tools with wafer residency time constraints in semiconductor manufacturing,”IEEE Trans.Semicond.Manuf.,vol.28,no.1,pp.117−125,Feb.2015.

[31]F.J.Yang,N.Q.Wu,Y.Qiao,and M.C.Zhou,“Petri net-based optimal one-wafer cyclic scheduling of hybrid multi-cluster tools in wafer fabrication,”IEEE Trans.Semicond.Manuf.,vol.27,no.2,pp.192−203,May 2014.

[32]F.J.Yang,N.Q.Wu,Y.Qiao,and M.C.Zhou,“Petri net-based polynomially complex approach to optimal one-wafer cyclic scheduling of hybrid multi-cluster tools in semiconductor manufacturing,”IEEE Trans.Syst.,Man,Cybern.Syst.,vol.44,no.12,pp.1598−1610,Dec.2014.

[33]L.P.Bai,N.Q.Wu,Z.W.Li,and M.C.Zhou,“Optimal one wafer cyclic scheduling and buffer space configuration for single-arm multicluster tools with linear topology,”IEEE Trans.Syst.,Man,Cybern.Syst.,vol.46,no.10,pp.1456−1467,Oct.2016.

[34]F.J.Yang,N.Q.Wu,Y.Qiao,and M.C.Zhou,“Optimal one wafer cyclic scheduling of hybrid multirobot cluster tools with tree topology,”IEEE Trans.Syst.,Man,Cybern.Syst.,to be published,doi:10.1109/TSMC.2016.2587697.

[35]Y.F.Chen,Z.W.Li,K.Barkaoui,N.Q.Wu,and M.C.Zhou“Compact supervisory control of discrete event systems by Petri nets with data inhibitor arcs,”IEEE Trans.Syst.,Man,Cybern.Syst.,vol.47,no.2,pp.364−379,Feb.2017.

[36]H.F.Chen,N.Q.Wu,and M.C.Zhou,“A novel method for deadlock prevention of AMS by using resource-oriented Petri nets”Inform.Sci.,vol.363,pp.178−189,Oct.2016.

[37]N.Q.Wu,“Necessary and sufficient conditions for deadlock-free operation in flexible manufacturing systems using a colored petri net model,”IEEE Trans.Syst.,Man,Cybern.,C Appl.Rev.,vol.29,no.2,pp.192−204,May 1999.

[38]N.Q.Wu and M.C.Zhou,System Modeling and Control with Resource-Oriented Petri nets.New York,USA:CRC Press,2009.

[39]N.Q.Wu,C.B.Chu,F.Chu,and M.C.Zhou,“A petrinet method for schedulability and scheduling problems in single-arm cluster tools with wafer residency time constraints,”IEEE Trans.Semicond.Manuf.,vol.21,no.2,pp.224−237,May 2008.