Development and Evaluation of a 7-DOF Haptic Interface

Jian-Long Hao,Xiao-Liang Xie,Gui-Bin Bian,Zeng-Guang Hou,Senior and Xiao-Hu Zhou

I.INTRODUCTION

HAPTIC interface is a robotic system through which human operators can touch and manipulate virtual objects or the remote environment.The most common type of haptic interfaces is the impedance controlled one which senses the operator’s motion and displays the appropriate feedback force to the operator[1].Low impedance(large motion in and low force out)can be easily realized through impedance type haptic interface.This intrinsic feature and the low implementation cost(no force or torque sensors needed)makes it a perfect choice for most applications.Two classical impedance controlled haptic devices are phantom series(3D SystemsCompany)[2],[3]and delta device series(Force Dimension Company)[4],[5].Detailed research on the phantom haptic device can be found in[6],[7].The other kind of haptic interface is the admittance controlled one(force in and motion out),which is generally used for applications requiring high force in a large workspace.

The high-end haptic devices developed by Force Dimension Company are based on delta structure[5].This parallel mechanism comprises one base platform,three identical chains and one moving platform,which provides three translational degrees of freedom.The main advantage of this architecture is its low inertia,the critical element of haptic device design,because its actuators can be mounted on the fixed platform.In addition,a mechanical wrist can be added to the moving platform to realize the rotational degrees of freedom.Since the moving platform of the delta mechanism is limited in a plane parallel to the base plane,the translation and rotation can be decoupled in mechanical structure.The Omega.7(Force Dimension Company)haptic device is a good instance of this idea[4].Other haptic devices with modified delta configuration are analyzed in[8],[9].In addition,haptic perception and understanding play extremely important roles in robot perception and interaction fields,latest research can be found in[10]−[12].

Adetuet al.[13]presented a computationally simple and compact inverse dynamic model for the Omega.3 parallel manipulator.However,the forward kinematics and control algorithms for haptic interaction are not discussed.Tobergte and Helmer[14]developed a disturbance observer and an interaction observer for the Sigma.7 haptic device(delta configuration and 7 active degree of freedoms(DOFs)).Wanget al.[15]and Liet al.[16]also introduced serial and parallel hybrid force feedback devices based on delta mechanism,however,only the mechanism and kinematics were described.Up to now,the dynamic modeling and its interaction control algorithm have not been fully studied in the literature to our best know ledge.In addition,the performance evaluation experiments of the haptic interface are also of great importance to characterize and improve itself.

This paper presents the dynamic modeling,controller design and performance evaluation of a 7-DOF haptic interface based on the modified delta mechanism.An impedance controller is designed and implemented on the prototype to realize the force feedback.A physical model based gravity compensation algorithm is proposed and validated through simulation and experiment.Experimental results show the good control performance of this interface.The remainder of this paper is organized as follows.Section II presents the kinematics and the gravity compensation algorithm.Section III presents an implementation of the prototype including the hardware system and the impedance control method.The validity of gravity compensation algorithm is demonstrated in Section IV.The control performance of the haptic interface is evaluated in Section V.The discussion and conclusion are followed in Section VI and Section VII respectively.

II.KINEMATICS AND GRAVITY COMPENSATION

A.Mechanism Description

The mechanical structure of the 7-DOF haptic interface is a series-parallel hybrid architecture comprised of one delta structure providing three translational DOFs,one serial wrist structure providing three rotational DOFs and one gripper unit providing one functional DOF.This structure is particularly suitable for haptic manipulator due to its high accuracy,high stiffness and mechanical decoupling between the translation and rotation.Three identical parallel chains of the delta structure separate each other by 2π/3 and connect the moving platform to the base platform by revolute joints.Each kinematic chain has a semi-circular capstan and a parallelogram connected by revolute joints.The semi-circular capstan is actuated by motor mounted on the base platform through cable.The mechanical wrist has a serial structure with an arrangement of three pivot joints having intersecting axes.Schematic of this mechanical structure is shown in Fig.1.

Fig.1.Schematic of the mechanical structure.The mechanism is composed of a delta structure providing three translational DOFs and a wrist structure providing three rotational DOFs and one gripping DOF.

B.Forward Kinematics

Forward kinematics describes the transformation of the position from the joint space to the Cartesian space,which is an essential step to realize the impedance control algorithm[17].The translation and rotation are decoupled thanks to the delta and wrist mechanism.The position of the end effector is determined by delta structure while the orientation is determined by the wrist.Therefore,the position and orientation can be calculated separately.

The position can be determined by three active joint angles between the semi-circular capstan and the base platform.To make it simple,one chain is taken for analysis as shown in Fig.2.The origin of the coordinate frame is set at the center point of the triangle which is composed of three active joints’centering point.Then,the kinematic equations of the first chain can be established and the other two can be obtained by multiplying a transformation matrix given by(1),where anglesφi=0°,120°,240°(i=1,2,3).According to the geometrical relationship and the geometrical parameters of the delta mechanism,the kinematic equations can be given by(2).The detailed mechanical structure analysis can be found in our previous work[18].

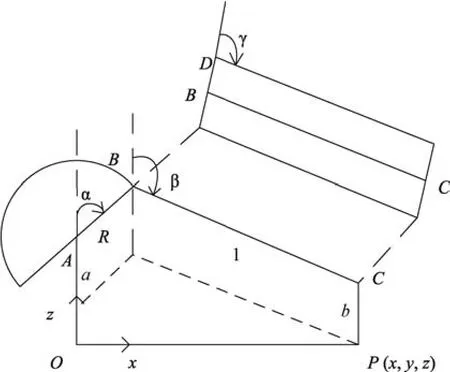
Fig.2.Geometric drawing of one chain for kinematic analysis.The coordinate origin is set to point O,the center point of triangle in Fig.1.Point P represents the position of the end effector.Joint variablesαandβare angles between axis z and the linkage respectively.Joint variableγis the angle between axis y and the linkage.

The serial wrist and its attached coordinate frame are shown in Fig.3.The orientation is determined by three rotational joint anglesθx,θy,θzabout axisxw,yw,zwrespectively.Using coordinate transformation,the orientation matrix of the wrist is calculated as(3),shown at the bottom of this page.The motor providing gripping force feedback is mounted on the handle.A small sector is connected with the motor shaft by steel cable.The gripping angle can be calculated through the reduction gear ratio.

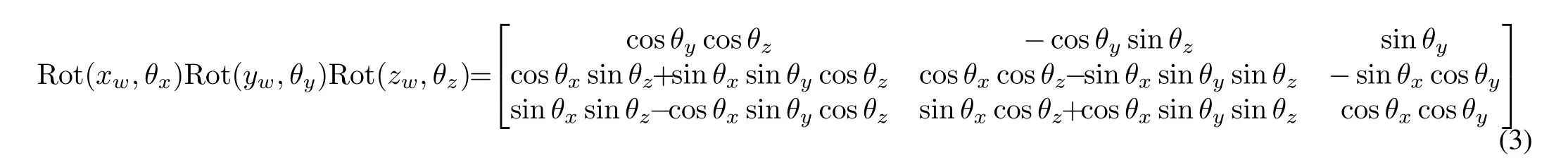
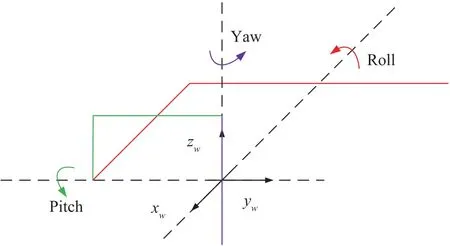
Fig.3.Geometric drawing of the wrist.Three rotational axes are perpendicular to each other and intersect at a point.The attached coordinate xw yw zw represents the orientation of the end effector.Its initial orientation is parallel to the base coordinate built in Fig.2.Joint angles θx,θy,θz describe the rotation transformation from the initial orientation to the final orientation.

C.Derivation of Jacobian

Jacobian matrix describes the transformation from the joint velocity to the Cartesian velocity.According to the virtual work principle,the transpose of the Jacobian matrix also provides static force transformation from the Cartesian space to the joint space.This is a critical step to transform the desired force at the end effector space to the joint torques in the joint space[17].The Jacobian matrix can be divided into two parts due to the decoupling kinematics.Besides,these three revolute axes of the wrist mechanism are mutually orthogonal,and its Jacobian matrix is a 3×3 identity matrix.The Jacobian matrix of the delta mechanism can be represented as(4):

whereviandwiare two auxiliary variables given by(5)and(6)[18].

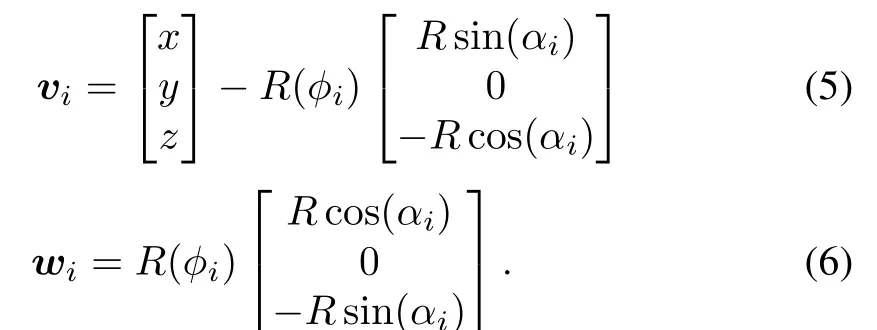
D.Gravity Compensation

Gravity Compensation plays an important role in haptic interface controller design.Regarding some manipulators designed for large workspace,the gravity compensation is indispensable for haptic interaction,because human operators may suffer from fatigue after a period of manipulation.Moreover,the physical interaction experience will be degraded dramatically by its inherent dynamics.However,a complete model,taking into account the masses and inertias of all links leads to very complicated solutions.Therefore,the problem is to find a solution which is sufficiently representative of the dynamic model and can be computed in real time.For simplifying the problem,the end effector(including the wrist mechanism)is treated as a point mass fixed at the moving platform of the delta mechanism.According to the previous work[19],the dynamic equation can be represented as follows:

whereTis a 3×1 joint actuation torque,Iis a 3×3 diagonal inertia matrix,αis a 3×1 joint angle vector,m eis the mass of the end effector part,Geis the gravity vector of the end effector part,TdandTpare torques introduced by the gravity force of semi-circular capstan and parallel linkages,respectively.

From(7),the following dynamic items can be defined:

whereMis the mass matrix of the manipulator,Cis the matrix of centrifugal and Coriolis terms,Gis the gravity item.

The gravity compensation algorithm is based on the itemG.To simplify the computational model,the mass of parallel linkages are assigned to the sem i-circular capstan part and the end effector part,which are all regarded as a point mass acting at the joint of semi-circular capstan and parallel linkages and the end effector respectively.Therefore,this computational model depends on the mass and length parameters of the mechanism.These three items are given by:

wherem dandmpare the masses of the semi-circular capstan and of parallel rods respectively,randRare the distance from the centroid of the semi-circular capstan to the revolute joint and the radius of the semi-circular capstan.

From the termG,it is clear that the gravity compensation torque is a function of Jacobian matrix.This gravity compensation algorithm highly depends on the physical model of the mechanism.The more accurate the physical model is,the better compensation performance can be expected.

III.IMPLEMENTATION

A.Hardware

In order to reduce the inertia,all linkages are made of light aluminum.Three identical chains connect the moving platform with the base platform.Three motors are mounted on the base platform and the semi-circular capstan of each chain is connected to the motor shaft with stainless steel w ire(diameter:0.75mm and construction:7×7).The wrist mechanism is added to the moving platform resulting in the decoupling of translation and rotation.The gripper is realized at the handle of the wrist mechanism with a fixed thumb thimble and a sliding index finger thimble.Similarly,the sliding thimble is connected with a motor embedded in the handle.Mechanical backlash is minimized thanks to the capstan transmission.Optical encoders are utilized to track the joint angles.The sensing resolution is high due to the high reduction ratio at active joints.

Three servo controllers(Escon 50/5,Maxon Motor,Switzerland)are used to drive motors mounted on the base platform.A low-power servo controller(Escon 36/2,Maxon Motor,Switzerland)is utilized to drive the gripper motor.All servo controllers are commanded by a micro controller(STM32F407,ST Microelectronics,Italy and France)through pulse width modulation(PWM)signal.All optical encoders are connected with the micro controller through the quadrature encoder interface of timers.Communications between the micro controller and the computer are performed at 1kHz through the universal serial bus(USB).The electrical system is shown in Fig.4.

Fig.4.Framework of electrical system.

B.Control

Generally,two classes of control schemes are appropriate for haptic interface:impedance control and admittance control.Impedance controlled systems sense the motion(displacement,velocity)commanded by the human operator and controls the force applied by the haptic interface.Conversely,admittance controlled systems sense the force commanded by the human operator and control the motion(displacement,velocity)of the haptic interface[17].Low impedance output is easily accessible by impedance control as long as the output force is set to zero.In addition,the cost of impedance controlled system is low since no force or torque sensors are required.Other variants of impedance control method can be found in[20].

The block diagram of impedance control method is shown in Fig.5.Optical encoders sense the joint angles and the position and orientation of end effector are solved through the forward kinematics.Interaction force in the virtual environment is calculated based on the stiffness and damping of virtual objects.Then,the desired feedback force is transformed to the joint torques through the transpose of Jacobian matrix.The gravity compensation algorithm computes the compensation torques based on the pose of the manipulator in real time.As shown in Fig.5,the haptic controller receives the joint angles and sends the torque commands to the motor controller.

Fig.5.Block diagram of impedance control.This type of force control is called “open loop”because there is no force feedback from the output to the controller.

IV.SIMULATION

In order to validate the effectiveness of the gravity compensation algorithm,MATLAB and Adams simulations have been performed.Adams is a powerful multi-body dynamic analysis software package which has been widely used in variety fields.A simplified virtual prototype of the modified delta manipulator is built in Adams software,where joint torques can be“measured”.The gravity compensation algorithm based on the physical model is implemented in MATLAB software.The algorithm is effective if there is little difference between the results from MATLAB and Adams under the same conditions.

In Adams software,three active joints are actuated and the joint torques are recorded while the virtual prototype maintains balance.A fixed force of 5.00N was acted at the end effector of the virtual prototype,which demonstrates the effectiveness of gravity compensation with force output at the end effector.For convenience,the desired output force is along thezaxis because gravity has a big influence on thezaxis.

Joint torques “measured”by Adams software are shown in Fig.6.The compensation torques calculated based on the physical model in MATLAB software are shown in Fig.7.The errors between the Adams results and the MATLAB results are shown in Fig.8.In Figs.6 and 7,it shows that torque of Joint 1 is greater than Joint 2 and Joint 3 and its torque direction is also opposite to the other two.The reason is that Joint 1 provides the pulling force and the other two provide the pushing force in the simulation.In addition,the overlapping curves of Joint 2 and Joint 3 validate their space symmetry.In Fig.8,it shows that torque errors are less than 0.03Nm,which is about 3%of actuation torque.Therefore,the simulation results validate the effectiveness of gravity compensation algorithm.

V.EVALUATION

In order to evaluate the haptic interface,experiments have been performed to validate the effectiveness of gravity compensation algorithm and determine the accuracy of the output forces.An experimental setup which is comprised of a lifting table and a 3-DOF force sensor(K3D120-50N,ME-systeme,Germany)has been developed.The force sensor is clamped on the lifting table and the supporting bar of the end effector is vertically fixed on the sensor.The output force of the end effector can be measured by the force sensor because the supporting bar is rigidly connected with the end effector.The experiment setup is shown in Fig.9.

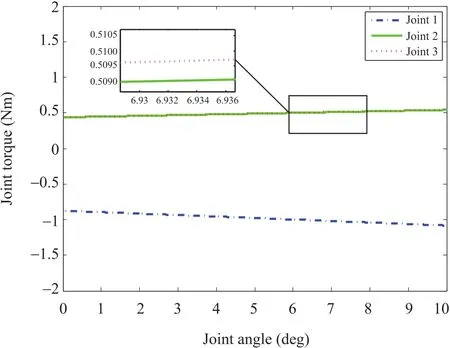
Fig.6.Gravity compensation torques in Adams software.The torque direction of Joint1 is opposite to that of the other two because Joint1 provides the pulling force.The magnitude is also larger because Joint1 provides more gravity compensation.

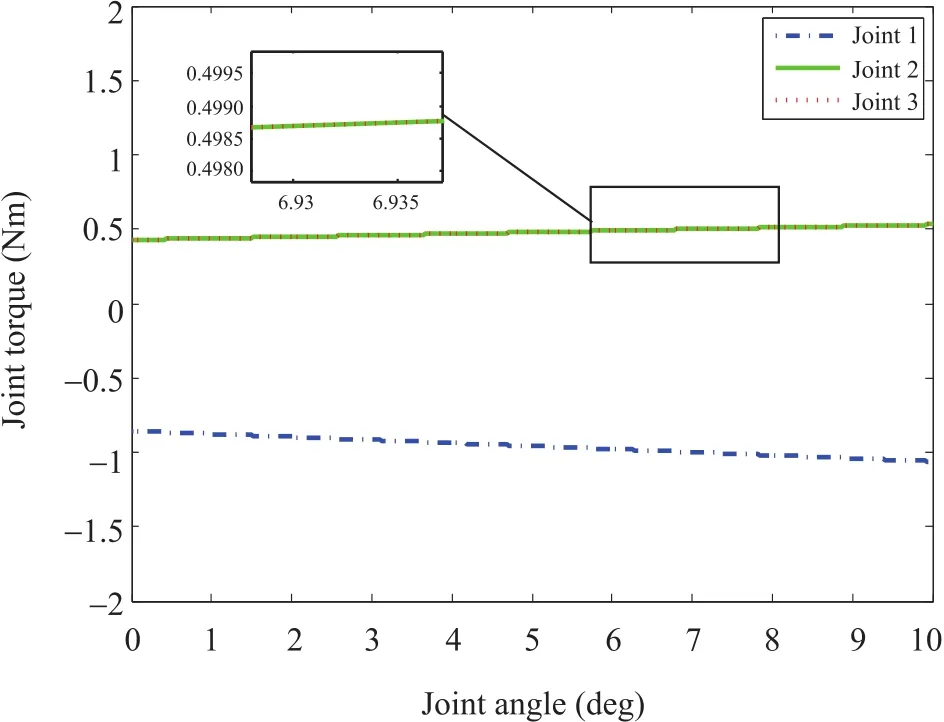
Fig.7.Gravity compensation torques in MATLAB software.Due to the symmetry of the two low chains,torques actuated at these two joints are the same ideally.The overlapping curves also manifest this point.

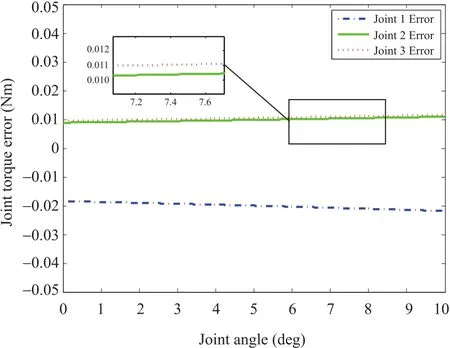
Fig.8.Gravity compensation error.Torque errors of three joints are all less than 0.03Nm.

Fig.9.Experiment setup.

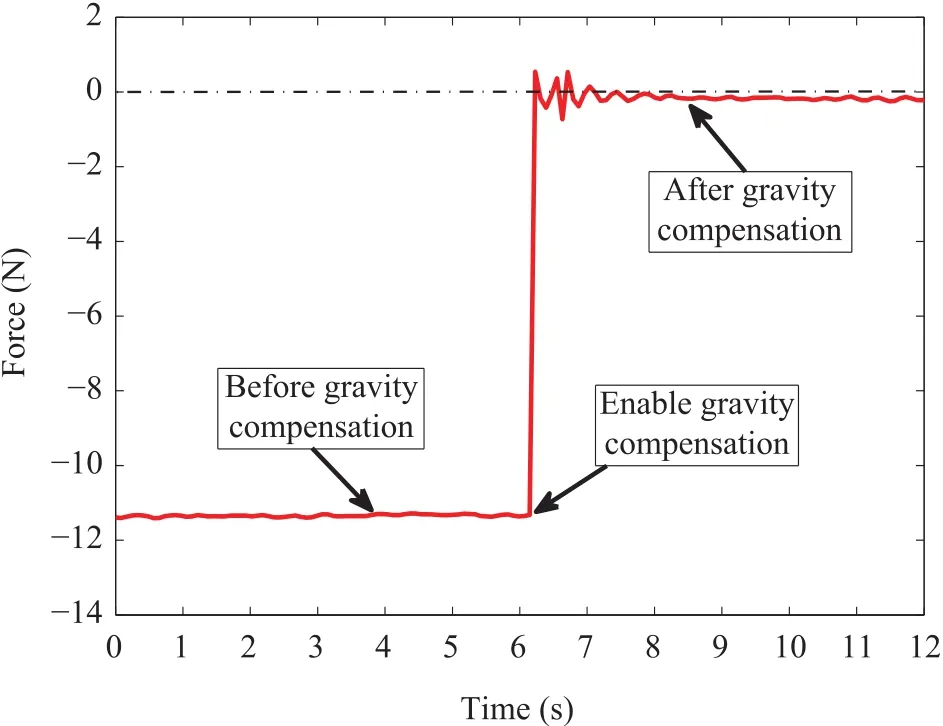
Fig.10. Gravity compensation response curve at the point(0.095,0.000,0.040)m.The pressure force measured by the sensor is decreased to nearly zero after gravity compensation is enabled.

A.Gravity Compensation

Gravity is an indispensable part for haptic interface controller design because the manipulator gravity leads to human operators’fatigue and degrades the interaction experience.A physical model based gravity compensation algorithm has been proposed for the haptic interface as discussed above.Some necessary simplifications are used to obtain a real-time computational model.In order to validate the effectiveness of the proposed compensation algorithm,gravity compensation experiments are conducted.It should be noted that since the supporting bar of the end effector is vertically fixed on the force sensor,the gravity force is along thezaxis direction.

The application program runs in a free mode and only the gravity compensation torque is commanded.The force sensor records the force change pre and post the gravity compensation.The response curve at position(0.095,0.000,0.040)m is shown in Fig.10.The gravity force is about 11N due to the large end effector with a wrist part and the long linkages of delta mechanism.After the gravity compensation is enabled,the force falls to almost zero with a rapid response.The gravity force is almost stationary before the compensation.This gravity force response curve shows that the gravity force is larger than 11N,which is prone to fatigue for human operator.Moreover,this large force can cause a seriousdisturbance to the feedback force,especially in the vertical direction.After the gravity compensation,there is a smallscope oscillation lasting to one second.This problem is mainly caused by the cable transmission which decreases the stiffness of the mechanical structure.Although,there is a little deviation between the final compensation force and the actual gravity force,it is insignificant and imperceptible for human operators.

TABLE I COORDINATES OF SAMPLE POSITIONS

In addition,the gravity compensation response curves are recorded at9 different positions onxplane.The coordinates of sample positions are given in Table I.The mean and standard deviation of gravity compensation errors at9 different sample positions onxplane are shown in Fig.11.From Fig.11,it can be noted that the mean error is less than 0.7N and errors are increased with thezcoordinates for givenycoordinates.

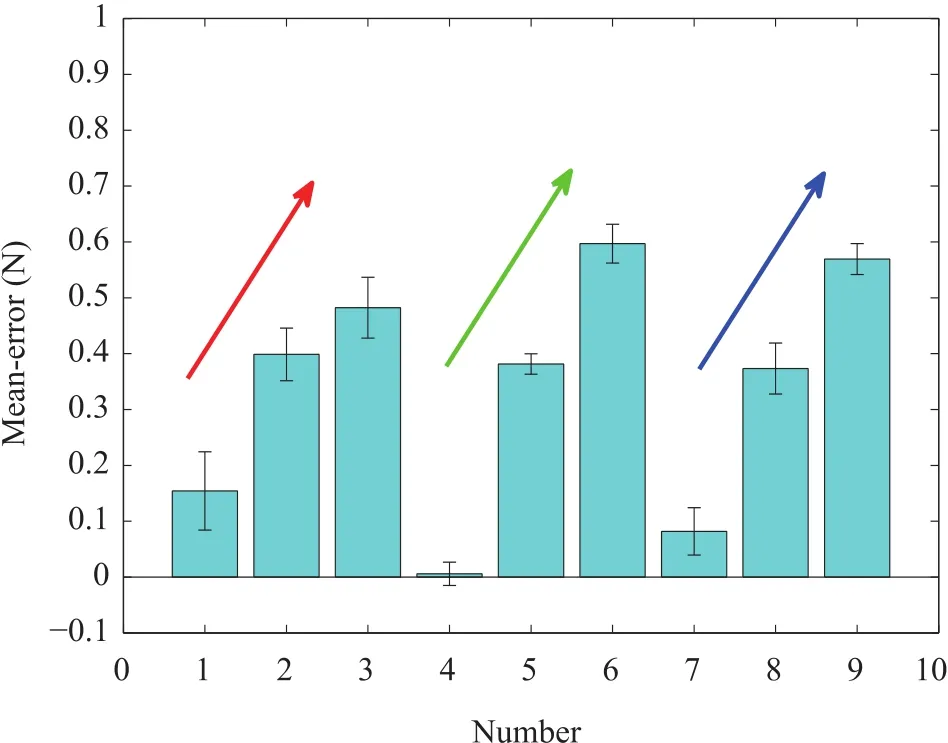
Fig.11.Gravity compensation error.The mean and standard deviation of gravity compensation errors at 9 different sample positions on x plane is shown.The coordinates of sample positions are given in Table I.Errors are increased with the z coordinates for given y coordinates.

The end effector can stay still in the workspace when it was placed there slowly.Since the gravity compensation algorithm highly depends on the physical model of the manipulator.The more accurate of the model is,the better performance can be obtained.On the other hand,the Coulomb friction plays a part in static balance of the end effector,which also makes it free of small disturbance.Theoretically,the Coulomb friction is indispensable to make the system less sensitive to quantization error introduced by position measurement[21].However,increasing friction decreases the accuracy and transparency of the haptic interface.

B.Static Response

The maximum output force of the haptic interface which limits its applications is an essential performance specification.Transient peak force is usually larger than the continuous force,but the former is limited in time due to heat dissipation.Therefore,the maximum continuous force is a better metric for haptic interfaces[22].

In order to measure the maximum continuous force at the end effector,the static response curves were recorded in the experiment.The end effector of this haptic interface was fixed at the center of the work space as a benchmark position.Output force commands were increased by 0.001N per millisecond and sent to the haptic controller.Motor current was increased to its nominal current and output force was recorded by the force sensor at a sampling rate of 12.5Hz.For convenience,output force direction was alongx,y,zaxis respectively.According to input and output force data,input-output force graphs were shown in Figs.12−14,respectively.Two sampling periods curves were plotted in each figure.The starting point was labeled in each figure and the commanded output force was changed along the blue arrows.

Fig.12. Input output force curve along x axis.Arrows indicate the direction of force change.The starting point is shown in the magnifier.

The ideal input-out put curve should be a45-degree diagonal line,implying a perfect match between the input force and the output force.However,the hysteresis loops in Figs.12−14 show the nonlinearity in the actuation system,which means the output force lags behind the input force.The worst case happens when the force direction changes,i.e.,two extreme points of this curve.The most probable reason is the mechanism backlash which can be amplified by the manipulator arm.The maximum hysteresis influence is alongxaxis and the minimal is alongzaxis.The maximum continuous output forces alongxandyaxis are up to±6 N and curves are symmetric with respect to zero point.However,due to gravity compensation,the input output force curve alongzaxis is not symmetric about zero point.The maximum value along the gravity can be up to 14N while the maximum upward output force is limited to 4N.The reason is that the main contribution

Fig.13. Input output force curve along y axis.Arrows indicate the direction of force change.The starting point is shown in the magnifier.

Fig.14. Input output force curve along z axis.Arrows indicate the direction of force change.The starting point is shown in the magnifier.The maximum continuous upward output force is restricted by the gravity compensation.of the motor is to provide gravity compensation.In addition,the Coulomb friction is another reason of the nonlinearity.

C.Force Tracking

The high performance of haptic interface means the good capability of force output as desired.However,the actual output force may be different from the desired force or the commanded force due to the dynamics of the haptic interface.To evaluate the accuracy of output performance,the increasing and decreasing triangular wave was commanded.The magnitude of the force was set to 5.00N.The results of force output inx,y,zaxis is shown in Figs.15−17,respectively.

In these figures,the actual output force curve drawn in red solid line and the commanded reference force curve drawn in black dash line are plotted in the same coordinate system.A ll these three recorded force tracking curves show a good waveform as commanded.The maximum force along theyaxis and the maximum output force along the negativezaxis are lower than the desired value.From zero seconds to five seconds in Fig.17,it shows that there is an upward bias along thezaxis because of gravity compensation.Another notable phenomenon is that the hysteresis occurs after the extreme point of the force curve.This happens because of the backlash of the mechanism.

Fig.15. Output force tracking along x axis.

Fig.16. Output force tracking along y axis.

Fig.17.Output force tracking along z axis.

Although these force tracking curves have a little deviation from the desired force curves,it is imperceptible and negligible for the human operators in the virtual interactions.A better performance may be expected if a force sensor is utilized in the control loop.Due to the high cost of force and torque sensors,an impedance controller providing a cost-effective way to realize the haptic interaction is important.Generally,the most difficult challenge is the gravity compensation because the human operator is sensible about the gravity which is usually large enough when a complex end effector is employed.In this experiment,the physical model based gravity compensation algorithm is proven to be effective.

V I.DISCUSSION

In this work,the dynamics analyses and control of a 7-DOF haptic interface have been researched.The main contribution of this work is the study of the realization of a haptic interface with multi DOFs in a cost effective way.It is a complicated problem because of the energy exchange between the physical human and the robot.From the control point of view,impedance control isan open loop force control because there is no force sensor at the end effector and no force feedback to the controller.Therefore,the output force is not equal to the desired force ideally.However,it is also the great advantage of impedance control.The development of haptic interface is restricted by the high cost of 3-DOF or 6-DOF force sensor.As a matter of fact,the human operator is not sensitive to the force scale in a limited range.Generally,the impedance of the virtual environment or rendered dynamics is modulated by human experience.

Another issue is that the controller presented above is based on the physical model as well as the gravity compensation algorithm.The more accurate the model is,the better output performance can be achieved.However,for more accuracy,the solution is more complicated and time-consuming.This presents a trade-off between the output performance and the computational efficiency.It is worthy to note that the sampling frequency(usually 1kHz)is critical to system stability[23].

In the evaluation experiments,all three force curves recorded by the force sensor show a small distortion at the extreme point.This happens because of the backlash of the mechanism which usually introduces inaccuracies and discontinuities of the perceived force when the commanded force or motion of the end effector changes direction.From the design point of view,the backlash in the joint parts can be magnified at the end effector due to long linkages.To reduce the backlash,capstan transmission is usually preferred.

V II.CONCLUSION

The dynamic modeling and control of a 7-DOF haptic interface have been presented in this research.An impedance controller with gravity compensation was proposed to realize the force feedback with high precision.A prototype with electrical system of sensing and actuation was implemented.To evaluate the control performance at the end effector,an experiment setup with a 3-DOF force sensor has been developed.The experiment results show that the maximum continuous output forces can be up to 6N alongxandyaxis and 4N alongzaxis.In addition,the effectiveness of gravity compensation algorithm was validated both in simulation and in experiment and the mean error of gravity compensation is less than 0.7N.This research presents a complete analysis of an impedance controlled haptic interface with multiple DOFs.The dynamic model and the haptic controller can be used or referenced for model based control systems to improve the performance further.The proposed haptic interface is also appropriate for haptic interaction and teleoperation applications.

ACKNOWLEDGMENT

The authors would like to thank Dr.Ying Shi for his advice on this work.

[1]C.R.Carignan and K.R.Cleary,“Closed-loop force control for haptic simulation of virtual environments,”Haptics-e,vol.1,no.2,pp.1−14,Jan.2000.

[2]3D Systems,USA.[Online].Available:http://www.geomagic.com/en/products-landing-pages/haptic

[3]T.H.Massie and J.K.Salisbury,“The phantom haptic interface:A device for probing virtual objects,”inASME Winter Annual Meeting,Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems,vol.55,pp.1−6,Jan.1994.

[4]ForceDimensionCompany, Switzerland. [Online]. Available:www.forcedimension.com

[5]S.Grange,F.Conti,P.Helmer,P.Rouiller,and C.Baur,“The delta haptic device,”2001.

[6]A.M.Tahmasebi,B.Taati,F.Mobasser,and K.Hashtrudi-Zaad,“Dynamic parameter identification and analysis of a PHANToM haptic device,”inProc.2005 IEEE Conference on Control Applications(CCA),Toronto,Canada,2005,pp.1251−1256.

[7]M.C.C¸avus¸ǒglu,D.Feygin,and F.Tendick,“A critical study of the mechanical and electrical properties of the phantom haptic interface and improvements for high performance control,”Pres.:Teleop.Virt.Environ.,vol.11,no.6,pp.555−568,Dec.2002.

[8]M.A.Ergin,A.C.Satici,and V.Patoglu,“Design optimization,impedance control and characterization of a modified delta robot,”inProc.2011 IEEE International Conference on Mechatronics(ICM),Istanbul,Turkey,2011,pp.737−742.

[9]W.K.Yoon,T.Suehiro,Y.Tsumaki,and M.Uchiyama,“Stiffness analysis and design of a compact modified delta parallel mechanism,”Robotica,vol.22,no.4,pp.463−475,Aug.2004.

[10]H.P.Liu,J.Qin,F.C.Sun,and D.Guo,“Extreme kernel sparse learning for tactile object recognition,”IEEE Trans.Cybernet.,2016,doi:10.1109/TCYB.2016.2614809.

[11]H.P.Liu,F.C.Sun,D.Guo,B.Fang,and Z.C.Peng,“Structured output-associated dictionary learning for haptic understanding,”IEEE Trans.Syst.Man Cybernet.:Syst.,vol.47,no.7,pp.1564−1574,Jul.2017,doi:10.1109/TSMC.2016.2635141.

[12]H.P.Liu,D.Guo,and F.C.Sun,“Object recognition using tactile measurements:Kernel sparse coding methods,”IEEE Trans.Instrum.Meas.,vol.65,no.3,pp.656−665,Mar.2016.

[13]C.F.Adetu,C.A.Moor,and R.G.Roberts,“Dynamic modeling and control of the OMEGA-3 parallel manipulator,”inProc.IEEE International Conference on Systems,Man and Cybernetics(SMC),San Antonio,TX,USA,2009,pp.3599−3604.

[14]A.Tobergte and P.Helmer,“A disturbance observer for the sigma.7 haptic device,”inProc.2013 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS),Tokyo,Japan,2013,pp.4964−4969.

[15]H.M.Wang,D.M.Wu,Z.J.Du,Z.Y.Yan,and C.J.Li,“Design of a novel serial and parallel force feedback master manipulator,”inProc.2010 IEEE Conference on Robotics and Biomimetics(ROBIO),Tianjin,China,2010,pp.1710−1715.

[16]Y.Li,Z.Y.Yan,H.M.Wang,Z.J.Du,and Y.C.Zhang,“Design and optimization of manipulator using series-parallel mechanism,”inProc.IEEE International Conference on Mechatronics and Automation(ICMA),Chengdu,China,2012,pp.2140−2145.

[17]B.Hannaford and A.M.Okamura,“Chapter 30:Haptics,”inSpringer Handbook of Robotics,B.Siciliano and O.Khatib,Eds.Berlin Heidelberg,Germany:Springer,2008,pp.719−739.

[18]J.L.Hao,G.B.Bian,X.L.Xie,Z.G.Hou,and H.N.Yu,“Kinematic and static analysis of a cable-driven 3-DOF delta parallel mechanism for haptic manipulators,”inProc.34th Chinese Control Conference(CCC),Hangzhou,China,2015,pp.4373−4378.

[19]J.L.Hao,X.L.Xie,G.B.Bian,Z.Q.Feng,Z.J.Gao,Z.G.Hou,H.N.Yu,and L.Vladareanu,“Dynamic modeling and control simulation of a modified delta manipulator,”inProc.2015 IEEE International Conference on Information and Automation,Lijiang,China,2015,pp.1573−1578.

[20]J.J.Gil and E.Sánchez,“Control algorithms for haptic interaction and modifying the dynamical behavior of the interface,”inProc.2nd International Conference on Enactive Interfaces,Genoa,Italy,2005.

[21]N.Diolaiti,G.Niemeyer,F.Barbagli,and J.K.Salisbury,“Stability of haptic rendering:Discretization,quantization,time delay,and Coulomb effects,”IEEE Trans.Rob.,vol.22,no.2,pp.256−268,Apr.2006.

[22]E.Samur,L.Flaction,and H.Bleuler,“Design and evaluation of a novel haptic interface for endoscopic simulation,”IEEE Trans.Hapt.,vol.5,no.4,pp.301−311,2012.

[23]J.J.Abbott and A.M.Okamura,“Effects of position quantization and sampling rate on virtual-wall passivity,”IEEE Trans.Robot.,vol.21,no.5,pp.952−964,Oct.2005.