Detecting Data-flow Errors Based on Petri Nets With Data Operations

Dongm ing Xiang,Guanjun Liu,,Chungang Yan,and Changjun Jiang

I.INTRODUCTION

BUSINESS process models pay attention to both control flow and data-flow[1].A good model contributes to the correctness verification of control/data-flows.Control-flow is concerned with the partial orders of tasks(e.g.,work flow process[2]),while data-flow focuses on data operations.Since a large number of data operations are executed in a business process,errors easily take place if the data-flow is designed improperly.These errors include missing data,redundant data,lost data,inconsistent data,and so on[3].Therefore,it is necessary and interesting to detect them.However,most existing studies mainly focus on the control-flow error detection,such as deadlock,livelock,infinite loop,lack of synchronization,compatibility,and soundness[4]−[8].This paper is about the data-flow error detection.

There have been some studies on data-flows.Sadiqet al.[9]propose seven kinds of data-flow anomalies,but do not provide any detection methods.Sharmaet al.[10]detect some data-flow errors based on business process modeling notation(BPMN).Guoet al.[11]address data exchange problems in the inter-organizational workflow,and calculate an exactdata set to ensure that the integrated workflow is free of dataflow errors.Sunet al.[12]use UML diagram to obtain the dependence relationship of business processes according to their data association,and then detect each process instance under some given rules.Their work is generalized in[13]and[6]where a systematic graph traversal approach is proposed to detect data-flow errors.These studies lack a completely formal semantics.The following work utilizes some formal methods to detect some data-flow errors.

A dual flow net(DFN)[14]models the control-and dataflows in an embedded system.Fanet al.[15]simplify DFN into dual workflow net in order to detect the soundness of business processes.Based on the work in[10],Awadet al.[16]map a BPMN into a Petrinet,and then detect and repair its errors.Although these formal models can represent the read/write operations,they are usually short of a complete semantics of concurrent read and/or coverable write.Contextual nets[17],[18]can represent concurrent read but not coverable write.In addition,some formal models like workflow nets with data(WFD-nets)[3]utilize label functions to describe data operations.They check the data-flow errors based on computation tree logic(CTL).However,this technique suffers from the state space explosion problem.

There exist some reduction techniques to alleviate the state space explosion problem.Partial-order methods,like persistent sets[19],ample sets[20]and stubborn sets[21],do a state space search in which a subset of transitions are computed and explored from each state.For an infinite state space of an unbounded Petri net,a new reduced reachability graph is proposed in[22]and[23].Instead of enumerating all the reachable states,symmetry reduction[24]gives equivalence classes of states w.r.t.the symmetry relation.The state hashing method(e.g.,Hash compaction[25],bit-state hashing[26])utilizes hash techniques to reduce memory usage,i.e.,each state is represented by hash values instead of full state representations.In the sweep-line method[27],some certain states of a system can be deleted based on a measure of progress.The above reduction techniques are used to verify some classical properties like reachability and deadlock rather than data-flow errors.This paper utilizes the reduction technique to detect the data-flow errors.

In this paper,we define a kind of Petri nets called Petri nets with data operation(PN-DO)that can model both concurrent read and coverable write.In order to detect data-flow errors,we construct a reachability graph with data operations for each PN-DO,and then present a detection algorithm.A new method is proposed to reduce the reachability graph.Based on the reduced reachability graph,the data-flow errors can be detected rapidly.Compared with our previous work in[28],we further detect redundant data and lost data.Most importantly,we propose a new method of reducing reachability graph to alleviate the state space explosion.

The rest of this paper is organized as follows.Section II introduces PN-DO.Section III defines 4 types of data-flow errors based on PN-DO.Section IV proposes an algorithm to detect data-flow errors based on the reachability graphs of PN-DOs.Section V gives a method to reduce the reachability graph in order to detect data-flow errors rapidly.Section VI shows a case study.The last section summarizes this paper.

II.PN-DO MODEL

This section first introduces read arcs and write arcs,and then gives the definition of PN-DO.

A.Read Arc

In the traditional Petri net,the operation of reading a data is described as a self-loop[18].For instance,t1andt2in Fig.1(a)both read the data from the placev1.However,selfloops cannot represent the concurrency semantics of reading the shared data[29].Since the placev1has only one token,only one oft1andt2is fired at one time,but they cannot be fired concurrently.Therefore,read operations are represented in the form of Fig.1(b)[30].In Fig.1(b),the dot line betweenv1andt1only represents that the token inv1is a condition of enablingt1,but it is not consumed whent1is fired.Hence,t1andt2can be fired concurrently.This paper uses the read arc in[29],[30].Notice that the two Petri nets in Fig.1 have the same reachability graph that is an interleaving-semantics based technique.If we indicate their differences under the concurrency semantics,we can use other techniques such as branching processes[17],[31],[32].

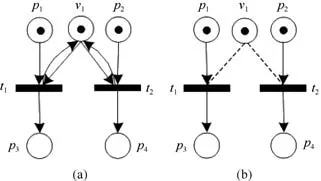
Fig.1:(a)Self-loop representing a read operation.(b)Read arcs.

B.Write Arc

W rite operations usually consider data-generation and/or data-update.Data-generation means that a variable is initialized via a write operation,i.e.,this variable has no value before this write operation is executed.Data-update means that the original value of a variable is replaced by a new value.

1)If Fig.2(a)is used to model a data-generation(i.e.,there is no token inv1),then a token is produced intov1aftertis fired.However,if there is a token inv1,v1has two tokens aftertis fired.Therefore,it cannot represent a data-update.

Fig.2:(a)Data-generation.(b)Data-update.(c)−(d)A write arc and its equivalent part.

2)If Fig.2(b)is used to model a data-update(i.e.,there is a token inv1),then there is still a token inv1aftertis fired.However,if there is no token inv1,thent1cannot be fired.This means that Fig.2(b)cannot represent a data-generation.

In summary,it is not easy to use a traditional Petri net to model both data-generation and data-update.

Fortunately,Petri nets with inhibitor arcs[33]can do this as shown in Fig.2(d).However,this model is too complex.In this paper we present a write arc as shown in Fig.2(c)that is simple obviously.Especially,for concurrent write operations,the reachability graph of our model is much simpler than that of Petri net with inhibitor arcs(e.g.,Fig.3 shows this).

Fig.3:Concurrent write operations.(a)−(b)A net with 3 write arcs,and its extended reachability graph.(c)−(d)The equivalent model with inhibitor arcs,and its reachability graph.

Some related models about writing data are existing.Vareaet al.[14]consider data-generation.Data-update is considered in[34]and[35].Although data-generation and data-update are both considered in[36]and[37]using a kind of write arc,they are about high-level Petri nets in which variables and their values are required by their write arcs.In this paper we focus on data-flows rather than the concrete variables and values,but we refer to the main ideas of[36]and[37].

C.PN-DO

N={0,1,2,...}is the set of non-negative integers.

Definition 1(N-DO):

A net with data operations(N-DO)is a 3-tupleN=(C∪V,T,F c∪F r∪F w∪F d),where

1)Cis the set of control places,Vis the set of data places,andC∩V=Ø;

2)Tis the set of transitions;

3)F c⊆C×T∪T×Cis the set of control arcs;

4)F r⊆V×Tis the set of read arcs;

5)F w⊆T×Vis the set of write arcs;and

6)F d⊆V×Tis the set of delete arcs such that

A marking of an N-DO is a mapping.A Petri net with data operations(PN-DO)is an N-DONwith an initial markingM0and denoted as

In a PN-DO diagram,a control arc is a line with an arrow,a read arc is drawn as a dashed line without arrows,and a write/delete arc is a dashed line with an arrow.For instance,Fig.4 shows a PN-DO,whereC={p1···p6},V={v1,v2},the arc fromp1tot1is a control arc,the dashed line fromv2tot4is a read arc,the dashed arc fromt1tov1is a write arc,the dashed arc fromv1tot3is a delete arc,and[p1;]is its initial marking.

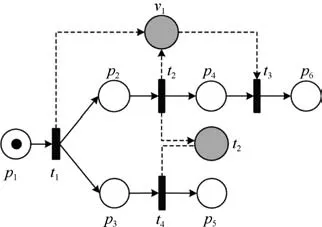
Fig.4:PN-DO.

The following notations are used in this paper:

1)c t={p|p∈C∧(p,t)∈F c}is a control pre-set oft;

2)t c={p|p∈C∧(t,p)∈F c}is a control post-set oft;

3)r t={v|v∈V∧(v,t)∈F r}is a read-set oft;

4)t w={v|v∈V∧(t,v)∈F w}is a write-set oft;

5)d t={v|v∈V∧(v,t)∈F d}is a delete-set oft;

6)PreD(t)=d t∪r t;

7)PostD(t)=t w.

Definition 2(Control-enabledness and Data-enabledness):Given a PN-DO

1)t∈Tis control-enabled at a markingM,which is denoted by.Otherwise,it is not control-enabled and denoted by

2)t∈Tis data-enabled at a markingM,which is denoted byM[v t〉,if∀v∈PreD(t):M(v)＞0.Otherwise,it is not data-enabled and denoted by¬M[v t〉.

Iftis control-enabled and data-enabled atM,then it is enabled atMand denoted asM[t〉.Otherwise,it is disabled and denoted byFiring an enabled transitiontatMyields a markingM′,and it is denoted byM[t〉M′such that∀s∈C∪V:

For example,at the initial marking[p1;]of the PN-DO in Fig.4,t1is enabled and after firing it,we get the marking[p2+p3;v1].At this marking,t4is control-enabled but not data-enabled sincev2has no token.

A markingM′is reachable from another markingM,if there exists a firing sequenceσ=t1t2···t nsuch thati.e.,M[σ〉M′.The set of markings reachable fromMis denoted byR(M).Notice thatt∈σmeans thattoccurs inσ.

Definition 3(Safeness):A PN-DO is safe if∀M∈R(M0),∀s∈C∪V:M(s)≤1.

This paper only considers the safe PN-DOs.There are two reasons why we only focus on the safe PN-DOs.First,it is not easy for us to define concurrency and conflict in a non-safe PN-DO.For example,if two transitions have the same input place(i.e.,conflict)and the place has multiple tokens(i.e.,they can concurrently occur),then their concurrency and conflict are not easily distinguished and thus our reduction technique cannot be used.Notice that the definitions of concurrency and conflict are given in the next subsection,and the reduction technique is given in Section V.The second reason is that many applications(like the example in Section VI)can be modeled by the safe PN-DOs.

D.Conflict Relation and Concurrency Relation

In a PN-DO,if two transitions are both enabled at a marking,then their relation is either conflict or concurrency.The two relations are determined by their control pre-set and marking distributions.

Definition 4(Conflict and Concurrency):Given a markingMof a safe PN-DO,two different transitionst1andt2are in

1)a conflict relation atM,which is denoted byifor

2)a concurrency relation atM,which is denoted byif

For example,t1andt2in Fig.5(a)are in a conflict relation at the initial markingM0=[p1+p2+p5;]since they satisfyandBy contrastandin Fig.5(b)are in a concurrency relation at the initial markingbecause they satisfyand

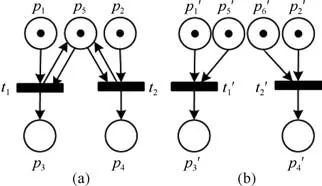
Fig.5:(a)Conflict relation.(b)Concurrency relation.

Obviously,the two relations satisfy symmetry but not transitivity.

III.DATA-FLOW ERRORS

Data-flow errors are caused by improper data operations,which mainly include missing data,redundant data,lost data,and inconsistent data.In the following definitions,is a safe PN-DO.

Fig.6:For the PN-DO Σ in Fig.4,its reachability graph,extended reachability graph,reduced ERG and prefixes are respectively:(a)RG(Σ);(b)ERG(Σ);(c)the reduced ERG;(d)−(g)the prefixes of

Definition 5(Missing Data):Σ has an error of missing data if

M issing data occurs when a process is reading or deleting some data,but this data is not existing at this time.In Fig.4,t4is control-enabled but not data-enabled at the reachable markingIt cannot read the data fromv2since there is no token inv2.At this time,missing data occurs.

Definition 6(Inconsistent Data):Σ has an error of inconsistent data if

Inconsistent data occurs when one process is reading or writing or deleting some data,but another process is concurrently writing or deleting this data.In Fig.4,at the reachable marking[p2+p3;v1],t2is writing a data intov2,butt4is readingv2concurrently.At this time,in consistent data occurs.

Definition 7(Redundant Data):Σ has an error of redundant data if one of the following two conditions holds:

Redundant data occurs if a data is never read before it is deleted or the business process terminates.In Fig.4,at the reachable marking[p2+p3;v1],t2is to overwrite the data ofv1.But the data has never been read before it is deleted byt3.Therefore,there is an error of redundant data.

Definition 8(Lost Data):Σ has an error of lost data if∃M1,M2∈R(M0),∃t1,t2∈T,∃σ∈T∗,∃v∈V:M1[t1σ〉M2[t2

Lost data means that a data has never been read before it is overwritten.In Fig.4,t1writes a data intov1.But this data has never been read before it is overwritten byt2.Therefore,this is an error of lost data.

IV.DATA-FLOW ERRORS DETECTION BASED ON PN-DO

This section first constructs the reachability graph of a PNDO based on its firing rules,then we extend the reachability graph via considering those transitions that are control-enabled but not data-enabled at some reachable markings.Finally,a detection algorithm for data-flow errors is proposed based on the extended reachability graph.

A.Reachability Graph

Definition 9(Reachability Graph,RG):Letbe a PN-DO.)is the reachability graph ofwhere

1)

2)such thatℓ(M i,M j)=〈t,r t,t w,d t〉if(M i,M j)∈EandM i[t〉M j.

For example,Fig.6(a)is the reachability graph of the PNDO in Fig.4.We know that the errors of missing data and inconsistent data occur at the reachable markingM1=[p2+p3;v1],but this reachability graph cannot directly indicate these errors.Therefore,in order to easily detect these errors,we extend the reachability graph,i.e.,a control-enabled but not data-enabled transition is added into the reachability graph.The related edges are drawn as lines with empty arrows.

Definition 10(Pseudo Reachable Marking):Letbe a PN-DO,M∈R(M0),andt∈T.Iftis control-enabled but not data-enabled,thenM′is called a pseudo reachable marking fromMviat,where

A pseudo reachable marking is yielded by operating control places only.We denoteM[c t〉M′ifM′is a pseudo reachable marking fromMviat.We add all pseudo reachable markings into the reachability graph and then get the extended reachability graph(ERG).The following definition is its formal representation.

Definition 11(Extended Reachability Graph,ERG):Let Σ=(C∪V,T,F c∪F r∪F w∪F d,M0)be a PN-DO,ERG(Σ)=(R(M0)∪R′(M0),E∪E′,ℓ∪ℓ′)is the extended reachability graph ofΣ,where

1)(R(M0),E,ℓ)is the reachability graph of

2)R′(M0)is the set of all pseudo reachable markings;

3)E′={(M i,M j)|M i∈R(M0)∧M j∈R′(M0)∧∃t∈T:M i[c t〉M j};and

4)ℓ′:E′→T×2V×2V×2Vsuch thatℓ′(M i,M j)=〈t,r t,t w,d t〉if(M i,M j)∈E′andM i[c t〉M j.

For example,Fig.6(b)is the ERG of the PN-DO in Fig.4,whereM3is a pseudo reachable marking such thatM1[c t4〉M3,(M1,M3)∈E′and

B.Data-flow Error Detection Based on ERG

A detection method for data-flow errors is proposed based on ERG,as shown in Algorithm 1.

Algorithm 1.Data-flow error detection algorithm

Procedure1 Detect IS Data(M,ConHash,ERG(Σ))

Procedure2 FindRWD(v,M′,ERG(Σ),M T)

1)In Algorithm 1,we first construct the ERG of a PN-DO and a hash-tableConHash.For each nodeMin the ERG,this hash-table stores all pairs of transitions that are in the concurrency relation atM,i.e.,

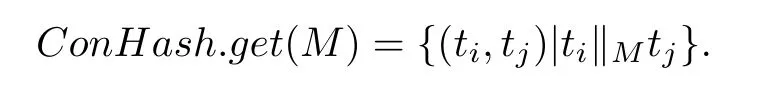
2)An edge inE′indicates an error of missing data.Based on this hash-table,we detect inconsistent data for concurrent transitions through the following function

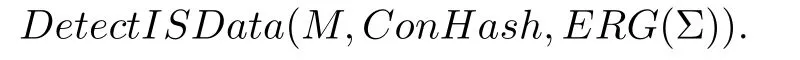
3)If a transition enabled at a marking is to write a data,we traverse all successors of this marking.Then,the markings related to operations on this data are obtained by the function

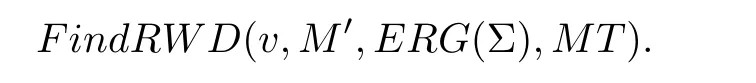
Finally,according to these markings,we determine whether there is an error of redundant data or lost data.

The time complexity of Algorithm 1 isO(W×K2),whereKrepresents the number of markings,andWdenotes the number of write arcs.Obviously,the detection complexity depends on the number of markings.However,the number of markings grows exponentially with the size of a net.Therefore,we propose a method to reduce an ERG.

V.A REDUCED ERG

Our reduction method depends on the following two facts.

1)When two concurrent transitions conduct operations on the different data,no data-flow error occurs.Therefore,for the multiple paths yielded by these concurrent transitions,only one can be kept in the reduced ERG.

2)When two concurrent transitions conduct the same operations on the same data(i.e.,concurrently write,or concurrently delete),an error occurs.At this time,each path in the ERG yielded by the two transitions can reflect this error.Therefore,we only need to keep one path in the reduced ERG for this case.

Notice that when two concurrent transitions conduct the different operations on the same data(e.g.,one is write,and another one is read),an error occurs too.However,the multiple paths yielded by the two transitions are all kept in the reduced ERG.If one path is deleted,this error possibly cannot be represented in the reduced ERG.

Our method is not to cut these paths after the ERG is produced.In fact,they are not yielded in the process of constructing the reduced ERG.In order to describe our algorithm,we need to introduce the following concepts.

Definition 12(Prefix):LetERG(Σ)=(R(M0)∪R′(M0),E∪E′,ℓ∪ℓ′)be the ERG of a PN-DO Σ.A prefix ofERG(Σ)is a subgraph of the ERG such thatM0is in the prefix,and for each nodeMof this subgraph,there is a directed path fromM0toMin the subgraph.

For example,Figs.6(d),(e)and(f)are three prefixes of ERG in Fig.6(b),where the prefix in Fig.6(d)has only the initial marking and is called the basic prefix.For convenience,a prefix of the ERG is denoted byG1=(R1,E1,ℓ1).

Definition 13(Possible Extension):LetERG(Σ) =(R(M0)∪R′(M0),E∪E′,ℓ∪ℓ′)be the ERG of a PN-DO Σ,G1=(R1,E1,ℓ1)be a prefix ofERG(Σ),andM∈R1be a node of the prefix.(e,M′)is a possible extension of the prefix atMife=(M,M′)∧e/∈E1∧e∈E∪E′.A new prefixG2=(R2,E2,ℓ2)ofERG(Σ)is generated after(e,M′)is added intoG1,where

1)R2=R1∪{M′};

2)E2=E1∪{e};

3)∀e′∈E1:ℓ2(e′)=ℓ1(e′),and.

For example,atM1of the prefix in Fig.6(e),there are two possible extensions((M1,M2),M2)and((M1,M3),M3).Adding the two possible extensions into this prefix,a new prefix is generated as shown in Fig.6(f).The notions of prefix and possible extensions refer to the work of unfolding of Petri nets[38],[39].

The idea of generating a reduced ERG is that starting from the basic prefix,we repeatedly add some possible extensions into it until no possible extensions can be added.Obviously,the key is that which possible extensions of a given prefix can be added and which ones cannot.

Given two possible extensions at a marking of a prefix,if the corresponding transitions are in the concurrency relation,then we should consider whether one of them is not added.If no inconsistent data exists in them,or there is an inconsistent data but they conduct the same operation on the same data,then we select one from the two possible extensions to add it into the prefix,while the other one is not added.Their formal descriptions are in selection criterion.Except for the above case,other possible extensions are added.

Selection Criterion:Let,ℓ∪ℓ′)be theERGof a PN-DO,andG1=(R1,E1,ℓ1)be a prefix ofERG(Σ),M∈R1,and(e1,M1)and(e2,M2)be two possible extensions of the prefix atMsuch that.If one of the two following conditions holds,one of the two possible extensions is added into the prefix and the other one is not.

1)There is no inconsistent data betweent1andt2;

2)there is an inconsistent data between them but they satisfy

For example,((M2,M4),M4)and((M2,M5),M5)are two possible extensions of the prefix in Fig.6(f)atM2.Because there is no inconsistent data betweent3andt4atM2,they satisfy selection criterion.Hence,((M2,M4),M4)is added into this prefix but((M2,M5),M5)is not,as shown in Fig.6(g).Certainly,we can also select the latter but not the former.By this method we can get a reduced ERG of the PN-DO in Fig.4,as shown in Fig.6(c).

Algorithm 2 illustrates the computation process of possible extensions,and its time complexity isO(Z2),whereZrepresents the number of enabled transitions at the markingM.Based on the reduced ERG,we can detect data-flow errors.The related algorithm is similar to Algorithm 1 and omitted here.

Algorithm 2.The possible extensions algorithm

8: P.add(x,y);9: if there exists(x,y)that does not satisfy selection criterion then 10: se=FALSE;break;11: end if 12: end for 13: if se==FALSE then 14: T S.add(S1∪{t1}∪S2∪{t1});15: else 16: if|S1|≤|S2|then 17: T S.add(S1∪{t1});18: else 19: T S.add(S2∪{t2});20: end if 21: end if 22:end for 23:if|T′|=1 or T co= Øthen 24: T S.add(T′);25:end if 26:for each t∈T S do 27: if M[t〉M1 then 28: S.add((M,M1),M1));29: end if 30: if¬M[v t〉and M[c t〉M2 then 31: S.add((M,M2),M2));32: end if 33:end for 34:return S

Our reduction method is suitable for these PN-DOs that have many concurrent transitions and satisfy the selection criterion.For example,Fig.7 shows the best reduction case.There are 9 pairs of concurrent transitions in Fig.7(a),and Fig.7(b)shows its ERG.Because all concurrent transitions satisfy the selection criterion,we can reduce most of markings and arcs,and then obtain reduced ERGs as shown in Figs.7(c)and(d).Obviously,due to different selections of possible extensions,the reduced ERGs are possibly not unique.

It is possible that some errors of inconsistent data cannot be reflected in a reduced ERG.For example,the error of inconsistent data caused by the concurrent transitionst3andt4is not be detected based on the reduced ERG in Fig.7(d),but it can be detected in view of the reduced ERG in Fig.7(c).This is because the concurrency structure oft3andt4is deleted in Fig.7(d)after((M2,M4),M4)is selected and added into a prefix at the markingM2.Hence,we cannot decide their concurrency relation and thus the error of inconsistent data cannot be checked.Therefore,the selection policy of possible extension is important,and we will improve it in the future work.

VI.CASE STUDY

We give a case study by referring to the business process in[6].This example is described as follows.

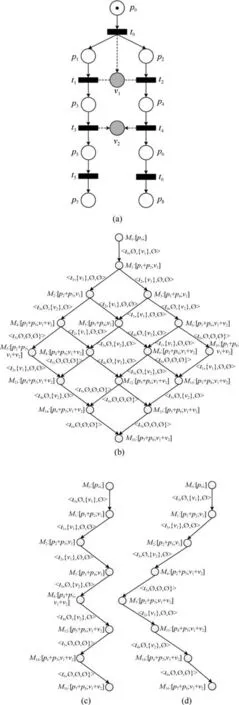
Fig.7:Different reduced ERGs.

A company seeks and publishes its write-ups every month.Hence,some selected employees are assigned to collect and write these reports.After write-ups are submitted to the group manager(GM),the GM decides whether these reports are accepted or sent back for revision.Once they are accepted,they can undergo the second review from the department head(DH);otherwise,these write-ups will be asked for revision and re-submitting.If these accepted reports fail to pass through the review from the DH,they will be asked to revise and resubmit to the DH.Otherwise,these write-ups are archived in the company’s software repository and go through editorial review.For the reports which have passed through all reviews,where to publish them(on the Web sites or in the newsletter)will be decided by the editorial review.Then,the write-ups selected for the newsletter will be catalogued to print publication.

In order to describe the business process of write-up publication,it is modeled by a PN-DO,and then its data-flow errors are respectively detected based on ERG and the reduced ERG.Now,the concrete procedures are listed as follows.

1)This business process is modeled by the PN-DO in Fig.8.The related data items and business activities are respectively shown in Tables I and II.

2)Fig.9 is its ERG and Fig.10 is its reducedERG.

3)According to Algorithm 1,its data-flow errors are detected and listed in Table III.

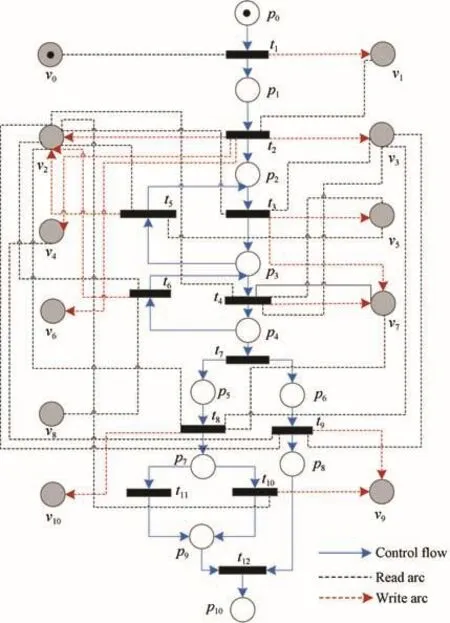
Fig.8:W rite-ups publication process(PN-DOΣ).

VII.CONCLUSION

Successful business process management depends on effective modeling and analysis.The model should consider both control-and data-flows,and the model checking technique should be effective.This paper proposes such a model and a technique.PN-DOs are defined to model both concurrent read and coverable write.A method of reducing their reachability graphs is proposed.Based on them,data-flow errors are detected rapidly.

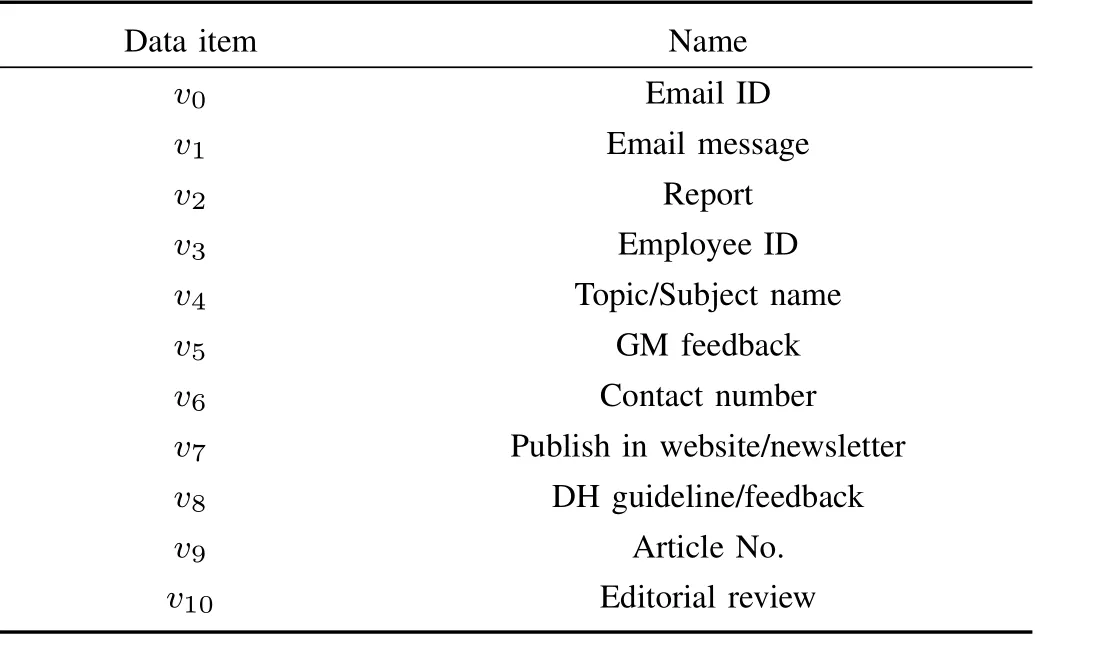
TABLE I DATA INFORMATION

TABLE II BUSINESS ACTIVITIES AND DATA OPERATIONS

In future work,we plan to improve the selection criterion that guarantees the reduced reachability graph can reflect all errors.Another work is to develop a software tool that uses the proposed algorithms to check the data-flow errors.We also plan to study the unfolding technique of PN-DOs to avoid state space explosion more effectively.

[1]C.C.Dolean and R.Petrusel,“Data-flow modeling:a survey of issues and approaches,”Inf.Econ.,vol.16,no.4,pp.117−130,Oct.2012.

[2]W.M.Van Der Aalst,“Workflow verification:finding control-flow errors using petri-net-based techniques,”inBusiness Process Management:Models,Techniques,and Empirical Studies,W.van der Aalst,J.Desel,and A.Oberweis,Eds.Berlin Heidelberg,Germany:Springer,vol.1806,pp.161−183,2000.

[3]N.Trčka,W.M.P.Van der Aalst,and N.Sidorova,“Data-flow antipatterns:Discovering data-flow errors in workflows,”inProc.21st Int.Conf.Advanced Information Systems Engineering,Heidelberg,Germany,2009,pp.425−439.

[4]W.M.P.Aalst,K.M.Hee,A.H.M.Hofstede,N.Sidorova,H.M.W.Verbeek,M.Voorhoeve,and M.T.Wynn,“Soundness of workflow nets:classification,decidability,and analysis,”Formal Aspec.Comput.,vol.23,no.3,pp.333−363,2011.

[5]G.J.Liu and C.J.Jiang,“Net-structure-based conditions to decide compatibility and weak compatibility for a class of inter-organizational workflow nets,”Sci.China Inf.Sci.,vol.58,no.7,pp.1−16,Jul.2015.

[6]H.S.Meda,A.K.Sen,and A.Bagchi,“On detecting data flow errors in workflows,”J.Data Inf.Qual.,vol.2,no.1,Article No.4,Jul.2010.

TABLE III DATA-FLOW ERRORS LIST

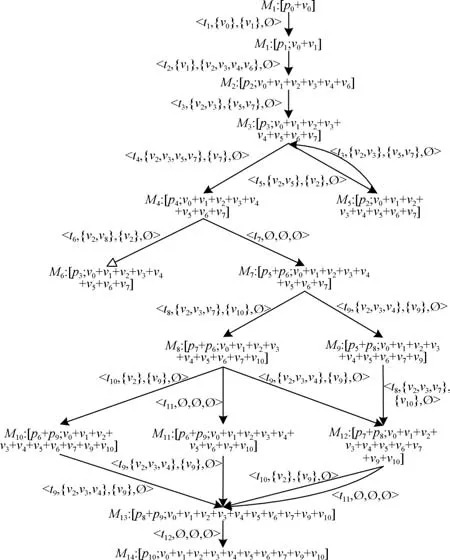
Fig.9:The ERG ofΣ.

[7]S.Roy,A.S.M.Sajeev,S.Bihary,and A.Ranjan,“An empirical study of error patterns in industrial business process models,”IEEE Trans.Serv.Comput.,vol.7,no.2,pp.140−153,Apr.−Jun.2014.

[8]S.G.Wang,M.D.Gan,and M.C.Zhou,“Macro liveness graph and liveness of omega-independent unbounded nets,”Sci.China Inf.Sci.,vol.58,no.3,pp.1−10,Mar.2015.

[9]S.Sadiq,M.Orlowska,and W.Sadiq,“Data flow and validation in workflow modelling,”inProc.15th Australasian Database Conf.,Dunedin,New Zealand,2004,pp.207−214.

[10]D.Sharma,S.Pinjala,and A.K.Sen,“Correction of data-flow errors in workflows,”inProc.25th Australasian Conf.Information Systems,Auckland,New Zealand,2014.

[11]X.T.Guo,S.X.Sun,and D.Vogel,“A dataflow perspective for business process integration,”ACM Trans Manage Inf.Syst.,vol.5,no.4,Article No.22,Mar.2015.

[12]S.X.Sun,J.L.Zhao,J.F.Nunamaker,and O.R.L.Sheng,“Formulating the data-flow perspective for business process management,”Inf.Syst.Res.,vol.17,no.4,pp.374−391,Dec.2006.

[13]H.S.Meda,A.K.Sen,and A.Bagchi,“Detecting data flow errors in workflows:A systematic graph traversal approach,”inProc.17th Annual Workshop on Information Technologies and Systems,Montreal,Canada,2007.

Fig.10:The reduced ERG of Σ.

[14]M.Varea,B.M.A l-Hashim i,L.A.Cortës,P.Eles,and Z.B.Peng,“Dual flow nets:modeling the control/data-flow relation in embedded systems,”ACM Trans.Embed.Comput.Syst.,vol.5,no.1,pp.54−81,Feb.2006.

[15]S.K.Fan,W.C.Dou,and J.J.Chen,“Dual workflow nets:m ixed control/data-flow representation for workflow modeling and verification,”inAdvances in Web and Network Technologies,and Information Management,K.C.C.Chang,W.Wang,L.Chen,C.A.Ellis,C.H.Hsu,A.C.Tsoi,and H.X.Wang,Eds.Heidelberg,Germany:Springer,vol.4537,pp.433−444,2007.

[16]A.Awad,G.Decker,and N.Lohmann,“Diagnosing and repairing data anomalies in process models,”inBusiness Process Management Workshops,S.Rinderle-Ma,S.Sadiq,and F.Leymann,Eds.Berlin,Heidelberg,Germany:Springer,vol.43,pp.5−16,2009.

[17]P.Baldan,A.Bruni,A.Corradini,B.König,C.Rodrïguez,and S.Schwoon,“Efficient unfolding of contextual Petrinets,”Theor.Comput.Sci.vol.449,pp.2−22,Aug.2012.

[18]U.Montanari and F.Rossi,“Contextual nets,”Acta Inf.,vol.32,no.6,pp.545−596,Jun.1995.

[19]R.Alur,R.K.Brayton,T.A.Henzinger,S.Qadeer,and S.K.Rajamani,“Partial-order reduction in symbolic state-space exploration,”inProc.9th Int.Conf.Computer Aided Verification,Berlin,Heidelberg,Germany,1997,pp.340−351.

[20]A.Lluch-Lafuente,S.Edelkamp,and S.Leue,“Partial order reduction in directed model checking,”inProc.9th Int.SPIN Workshop on Model Checking of Software,Grenoble,France,2002,pp.112−127.

[21]A.Valmari and H.Hansen,“Can stubborn sets be optimal?,”inProc.31st Int.Conf.Applications and Theory of Petri Nets,Berlin,Heidelberg,Germany,2010,pp.43−62.

[22]S.G.Wang,M.C.Zhou,Z.W.Li,and C.Y.Wang,“A new modified reachability tree approach and its applications to unbounded Petrinets”.IEEE Trans.Syst.Man Cybern.Syst.,vol.43,no.4,pp.932−940,Jul.2013.

[23]S.G.Wang,M.D.Gan,M.C.Zhou,and D.You,“A reduced reachability tree for a class of unbounded Petri nets,”IEEE/CAA J.Autom.Sin.,vol.2,no.4,pp.345−352,Oct.2015.

[24]P.A.Bourdil,B.Berthom ieu,S.D.Zilio,and F.Vernadat,“Symmetry reduced state classes for time Petri nets,”inProc.30th Annu.ACM Symp.Applied Computing,Salamanca,Spain,2015,pp.1751−1758.

[25]M.Westergaard,L.M.Kristensen,G.S.Brodal,and L.Arge,“The ComBack method:extending hash compaction with backtracking,”inProc.28th Int.Conf.Application and Theory of Petri Nets,Berlin,Heidelberg,Germany,2007,pp.445−464.

[26]G.J.Holzmann,“An analysis of bit state hashing,”Formal Methods Syst.Des.,vol.13,no.3,pp.289−307,Nov.1998.

[27]S.Christensen,L.M.Kristensen,and T.Mailund,“A sweep-line method for state space exploration,”inProc.7th Int.Conf.Tools and Algorithms for the Construction and Analysis of Systems,Berlin,Heidelberg,Germany,2001,pp.450−464.

[28]D.M.Xiang,G.J.Liu,C.G.Yan,and C.J.Jiang,“Checking the inconsistent data in concurrent systems by petri nets with data operations,”inProc.IEEE 22nd Int.Conf.Parallel and Distributed Systems(ICPADS),Wuhan,China,2016,pp.501−508.

[29]W.Vogler, “Partial order semantics and read arcs,”inProc.22nd Int.Symp.Mathematical Foundations of Computer Science,Berlin,Heidelberg,Germany,1997,pp.508−517.

[30]W.Vogler,“Efficiency of asynchronous systems and read arcs in Petri nets,”inProc.24th Int.Colloquium on Automata,Languages,and Programming,London,UK,1998,pp.538−548.

[31]G.J.Liu,W.Reisig,C.J.Jiang,and M.C.Zhou,“A branching-process based method to check soundness of workflow systems,”IEEE Access,vol.4,pp.4104−4118,Jan.2016.

[32]W.Vogler,A.L.Semenov,and A.Yakovlev,“Unfolding and finite prefix for nets with read arcs,”inProc.9th Int.Conf.Concurrency Theory,London,UK,1998,pp.501−516.

[33]S.Christensen and N.D.Hansen,“Coloured Petri nets extended with place capacities,test arcs and inhibitor arcs,”inProc.14th Int.Conf.Application and Theory of Petri Nets,London,UK,vol.691,pp.186−205,1993.

[34]S.Bandinelli and A.Fuggetta,“Computational reflection in software process modeling:the SLANG approach,”inProc.15th Int.Conf.Software Engineering,Los Alamitos,CA,USA,1993,pp.144−154.

[35]L.Ma and J.P.Tsai,“Formal modeling and analysis of a secure mobile agent system,”IEEE Trans.Syst.Man Cybern.A Syst.Hum.,vol.38,no.1,pp.180−196,Jan.2008.

[36]J.Desel,V.M ilijic,and C.Neumair,“Model validation in controller design,”inLectures on Concurrency and Petri Nets,J.Desel,W.Reisig,and G.Rozenberg,Eds.Berlin Heidelberg,Germany:Springer,2004,pp.467−495.

[37]C.X.Xu,W.L.Qu,H.P.Wang,Z.Z.Wang,and X.J.Ban,“A petrinet-based method for data validation of web services composition,”inProc.IEEE 34th Annu.Computer Software and Applications Conf.,Washington,DC,USA,2010,pp.468−476.

[38]B.Bonet,P.Haslum,V.Khomenko,S.Thiëbaux,and W.Vogler,“Recent advances in unfolding technique,”Theor.Comput.Sci.,vol.551,pp.84−101,Sep.2014.

[39]J.Esparza,S.Römer,and W.Vogler,“An improvement of McMillanś unfolding algorithm,”Formal Methods Syst.Des.,vol.20,no.3,pp.285−310,May2002.