Event-triggered MPC Design for Distributed Systems With Network Communications

Xiaoxiao Mi and Shaoyuan Li

I.INTRODUCTION

ALTHOUGH the wireless network can reduce the cabling cost and rapidly reconfigure the communication infrastructure in case of changing the system structure,the incorporation of this network into the distributed control poses new challenges to the control design.

On one hand,each local controller in the distributed systems decides on its current control action not only based on its own information,but also the shared information by others to improve the overall performance.These dynamical interaction among the controllers causes a tremendous amount of information transmitted through the network,especially when using the iterative algorithms[1],[2].This increases the requirement for the network.On the other hand,the wireless nodes with limited battery power supply and limited bandwidth can’t afford the mass transmission load and may lead to the network interruption,such that the system performance is degraded.In addition,it’s shown that data transmission between nodes has an energy consumption much higher than the processing,and the energy consumption in the reception and idle states is of the same order of magnitude as in the transmission[3].These considerations motivate the need of reducing the communication rate while promising the performance.

Lots of research have been done to deal with the problem aforementioned.From the angle of control design,event triggered mechanism is introduced,which is different from the traditional time-triggered control.That is,in the event triggered control,the wireless nodes perform their tasks if and only if an event occurs rather than the period manner.It avoids the unnecessary communication and realizes a good trade-off between the system performance and resources utilization.

Significant contributions have been made to the literature of event-triggered control,see[4]−[6]and the references therein.Specifically,a new method to design the triggering condition is presented based on the small-gain theorem for the nonlinear continuous systems in[5].But the system states are continuously monitored in these event-triggered mechanisms.To further reduce the energy consumption of sampling,a self-triggered scheme is provided in[7].Compared with the event-triggered control,the self-triggered control is proactive and computes the next sampling time or actuation instant ahead of time,so that the sensor nodes can keep in sleep mode before the predicted time.A periodic event-triggered control proposed in[8]−[9]can also avoid monitoring the triggering condition continuously.The event-triggered control strategy has developed rapidly and been applied to many fields recently[10]−[12].[10]applied this strategy to the masters lave coupling systems with heterogeneous dimensions,thus the communication cost is reduced by only transmitting some of the states of the master system to the slave system.A co-design algorithm for determining the parameters of the triggering scheme and the consensus controller gain is also presented in[11].Besides,the model predictive control(MPC)strategy is applied in[7]and a predictor is introduced in[8]to reduce communication by exchanging the predicted states with neighbors.

As well known,MPC is widely spread for control design of highly complex multi-variable processes with constraints.But as a receding horizon control method,the controller solves a finite horizon optimal problem every time,which motivates the event-triggered MPC study to reduce the unnecessary optimization,see[13]−[18].It is shown that the practical implementation of wireless MPC based on event is validated,and is beneficial for experimental complex process in[15]with an operation on a divided wall column.Despite the vast literature on event-based control in the context of networked control systems,no results on event-based communication in distributed MPC are available at the moment[17],[18].

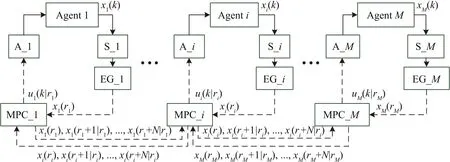
Fig.1.Structure of event-based MPC in wireless network.

In this paper,we deal with the communication problem in the constrained distributed systems,consisting of linear time-invariant agents with a cooperated objective.The event triggered MPC strategy is adopted,since it can not only reduce the transmission frequency,but also deal with system constraints and multi-objectives.The challenge is how to design a triggering condition to allow a substantial reduction of transmission without deteriorating the system performance.

The main contributions of this work are two-fold:

1)A triggering condition has been provided for the discrete time linear systems based on the Lyapunov stability analysis.Here,to reduce the triggering times as much as possible,an event and transmission happen only when the Lyapunov function will exceed the value at the last updating time,and it may increase in few times,but an average decrease is guaranteed aiming at stabilizing the system.

2)Since the feasible region of the optimal control problem is very small with a short prediction time.But the accuracy of the predicted states decreases with the horizon length,and an overlarge prediction horizon affects the quickness of control scheme.Considering these cases,we optimize and minimize the terminal constrained set in the maximal control invariant ellipsoid set to expand the feasible region.And the stability is guaranteed as long as the initial state is feasible.

The organization of this paper is as follows.Section II introduces the basic event-triggered MPC strategy.Then in Section III,we propose an event-triggering condition,and design an event-triggered MPC strategy for the distributed system to reduce frequent communication.The feasibility and stability are also analyzed in Section III.Finally,a simulation is provided to verify the theoretical results in Section IV.Section V gives the conclusion and future directions of this research.

Notations:Throughout the paper,Rndenotes thendimensional Euclidean space.The notationP≻0 means that matrixPis a positive definite matrix.The symbol“∗”denotes the symmetric term in a symmetric matrix.The superscripts“T”and “−1”represent the matrix transposition and inverse,respectively.The subscript“i”represents theith agent.We useto represent the Euclidean norm of a vectorx∈Rnand also the induced norm of a matrix.

II.BASIC EVENT-TRIGGERED MPC STRATEGY

The distributed system considered consists ofMagents with a locally cooperating objective.The agents are modelled by the discrete-time linear system

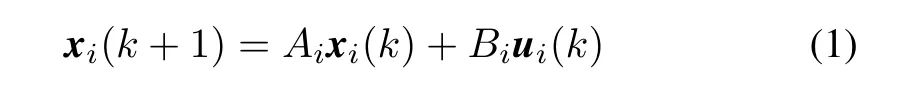
wherek∈Z is the time step andi=1,...,M,xi(k)∈Rnidenotes the state of theith subsystem at timek,andui(k)∈Rmithe control input.AiandBiare constant matrices with appropriate dimensions.Besides,the control inputs are constrained in a compact set asui(k)∈Ui,and the statesxi(k)∈Xi.Both Uiand Xicontain the origin.Assume that the pair(Ai,Bi)is controllable,and(Ai,Ci)is observable.

In this paper,we focus on the communication network between sensors,controllers and the correlative agents.And each agent is controlled by an event-triggered MPC controller to reduce the communication rate over the wireless network,which forms a distributed MPC framework,see Fig.1.The basic idea of this strategy is as follows.

Remark 1:In Fig.1,“Ai”and “Si”are short for actuator and sensor in theith agent,respectively.ridenotes the last triggering time in theith agent in Fig.1.The sequence{xi(ri),xi(ri+1|ri),...,xi(ri+N|ri)}is the information transmitted to its neighbors at the updating timeri.The wireless communication channel among nodes considered in this work is represented by the dotted line.

At time step k,the wireless sensor nodes in the i th agent transmit the measurement xi(k)to its controller if and only if||xi(k)−i(k)||≥ εi,where the design parameter εi(＞ 0)denotes the deviation threshold,i(k)shows the prediction of the current states.Then the i th agent solves a locally cooperated optimal problem(2)to determine its current control action,and transmits the corresponding predictive state trajectory to its neighbors.

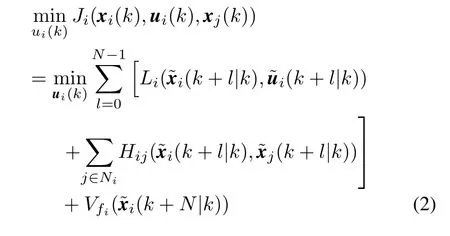
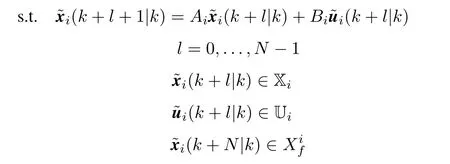
where

is the target terminal set,andandRiare the weighting matrices in the local cost function,coupling function,the terminal cost function and the input penalty,respectively.And assume that they all are symmetric positive definite matrices,denoted asandThe vectordenotes the prediction states based on the measurement of the state at timek,which is a dependent variable and computed by solving the optimal problem.AndN iis a set of indexes of agents theith agent communicates with,wherei/∈N i.

It’s worth noting that the thresholdεiis a critical tuning knob of the approach since it trades off the system performance and communication rate over the wireless channel.In this paper,our purpose is to design such a triggering condition to achieve a good trade-off.And we expect that the triggering condition can reduce the controller updating and communication resources largely,and also indicate the system performance dynamically.

III.EVENT-TRIGGERED MPC ALGORITHM DESIGN

In this section,the triggering condition will be provided based on the Lyapunov stability analysis.Then an improved scheme is put forward to expand the feasible region.And the whole control algorithm is introduced.Firstly,some standard conditions for design parameters of the event-triggered MPC in distributed systems must be introduced,in order to assert that this strategy can result in a stabilizing controller.Assumption 1:The stage functionLi(xi,ui)is Lipschitz continuous in Xi×Ui.That is,∀x1i∈Xiand

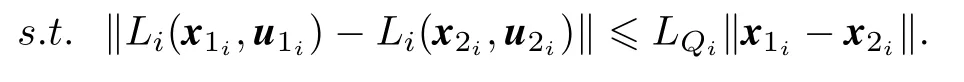
Assumption 2:The running costis Lipschitz continuous in Xi×Xj,with Lipschitz constantsandrespectively.

Assumption 3:There exists an invariant set,denoted asAnd the terminal setsuch that

Assumption 4:Ifthere exists a local stabilizing controllerin the sense thatIn addition,,we have,and the associated terminal function has the following property

Assumption 5:The terminal costVfi(xi)is Lipschitz continuous inwith constantLfi.

Assumption 6:Idealize the wireless communication channel,neglect data loss and delays.Also,the latency and jitter issues are not considered in the wireless network.

A.Triggering Condition Design

For the system in(1),define the series{ri}(ri∈N)as time instants when the optimization problem needs to be solved.The optimal control sequence and the optimal state trajectory at the triggering timeriare denoted byAt sampling timeri+m(m=1,...,N−1),we construct a control trajectorybased onsee(3).Concretely speaking,the corresponding inputs inare applied to the constructed predicted inputs during time(ri+m,ri+N−1).After timeri+N,the control action is computed by the feedback control law according to the predicted states.If no event is triggered at timeri+m,take the current control action in(3);otherwise,update the control action by solving the optimization problem(2).

By recursive procedure,the feasibility of the control sequencecan be easily proved as long as the initial state is in the feasible region.In addition,the designed control trajectory is independent of the states between timeriandri+m−1,so that this mechanism can be extended to a self-triggered formulation to avoid monitoring the states continuously.

With these preliminaries,a lemma is presented.

Lemma 1:Consider the system(1)with the optimal control problem(2).Suppose that Assumptions 1−6 hold,and the optimal problem of theith agent is solved at timeri,and the minimal index isDefineas the performance under the constructed feasible control actions(3).We have that,if there is no information received from its neighbors,the difference between andis bounded by

Otherwise,

where

rj=arg minrj{ri−rj＞0}is the last triggering time of

thejth agent at timeri,andis that of thejth agent at current timeri+t.|N i|denotes the number of its neighboring agents.

Proof:In this proof,we will prove that for anyt=1,...,N−1,the(4)or(5)always holds.First the inequality(4)is proved,and then the inequality(5)by the same procedure.

First,assume that there is no information received from its neighbors between timeriandri+t,thus the future states of its neighbors are all predicted based on the states at the same time.Then the performance difference between the cost functions at the current time and the last triggering time is

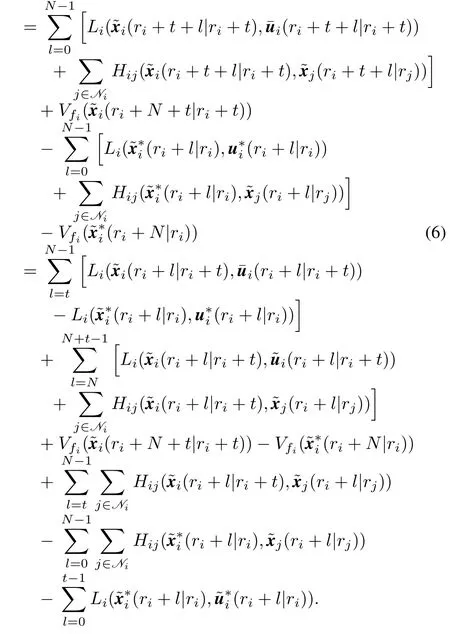
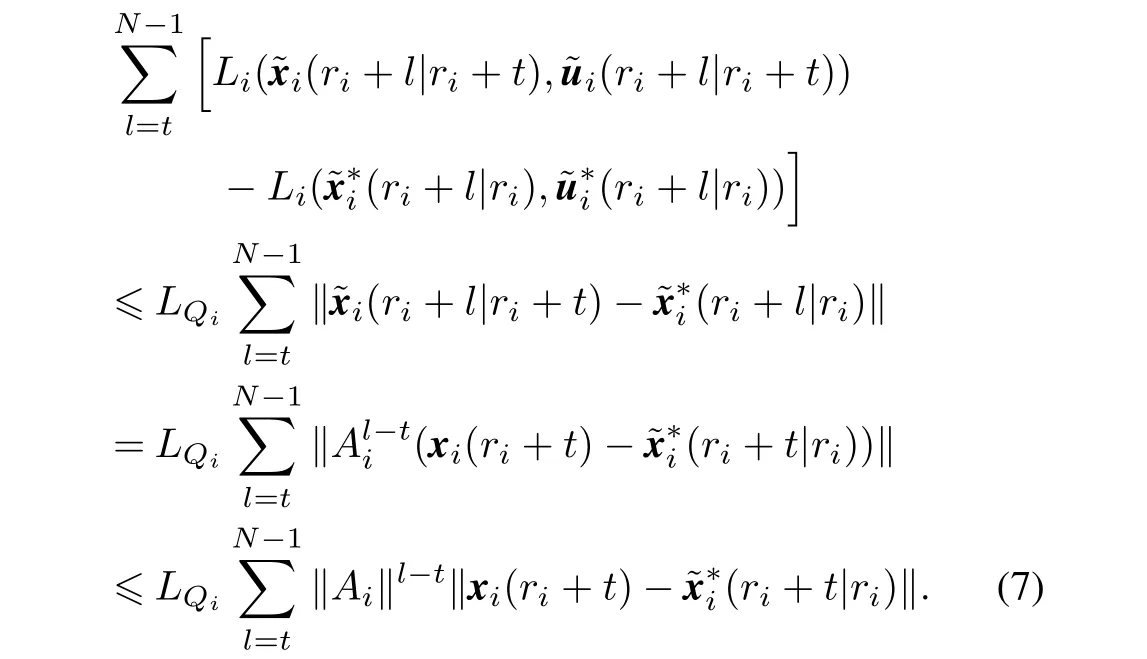
According to the Assumption 4,we get

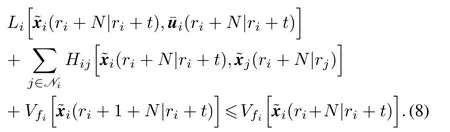
Similarly,a series of in equations can be found

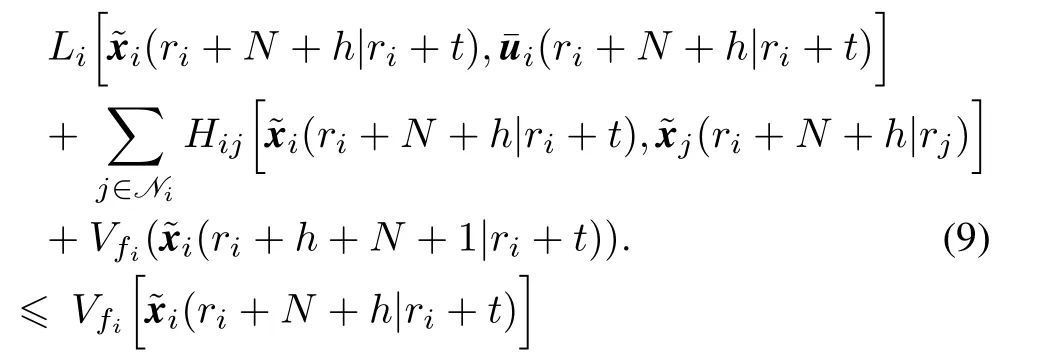
withh=0,...,t−1.

Summing all the inequalities in(9),we have

From the above deduction and the Assumption 5,the following inequality holds

Since there is no communication among the neighbors during time(ri,ri+t),such that the predicted states of the neighbors are the same during time(ri+t,ri+N−1).Then based on the Assumption 2,we have,forl=t,...,N−1

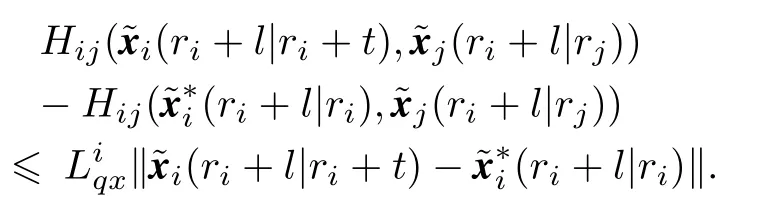
Therefore,

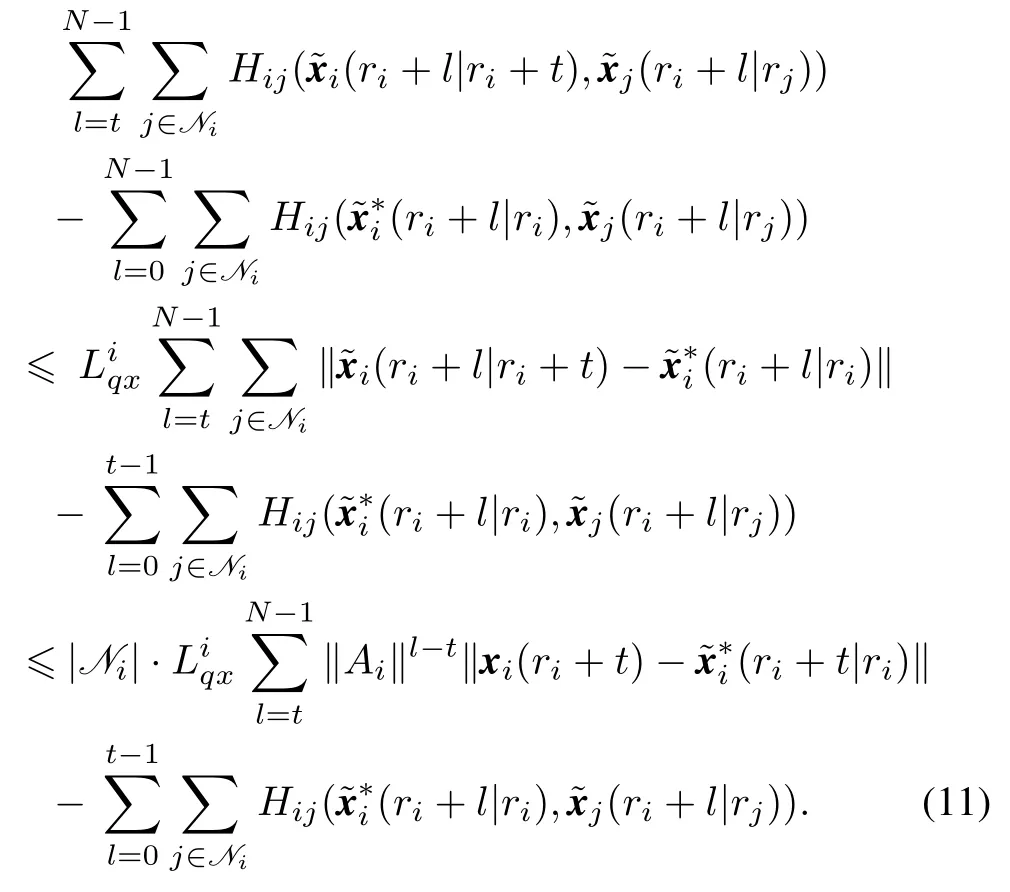
By summarizing the inequality(7),(10)and(11),the difference between the performance indexes is bounded,which completes the proof of inequality(4).

If thejth agent sends its current information to theith subsystem atwe get that,with the similar procedure

Summarizing the inequality(7),(10)and(12),the inequality(5)is proved.

Based on Lemma 1,the performance difference relates to the optimal state trajectory at the last triggering time and the current states.If we enforce the condition

and

with 0＜β＜1,we getThus,the event triggering condition of theith agent is

or

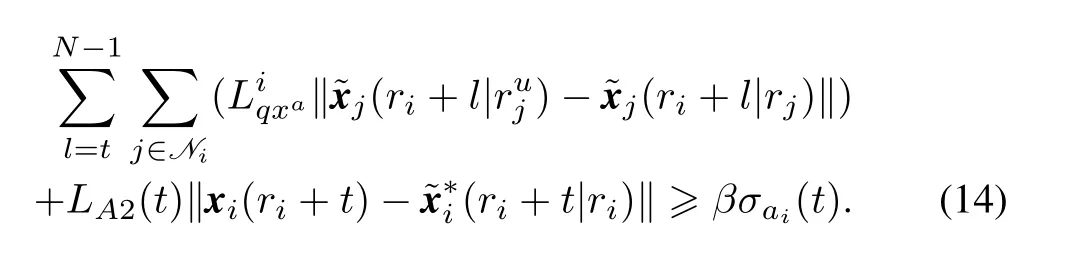
The triggering conditions(13)and(14)are just like a switch to determine whether the sensor sends the current information to the controller or not,and check if the neighboring agents exchange information with each other.At the initial time,the sensor transmits the system states to the controller and the neighboring agents exchange their states with each other to compute the control sequence and the predicted state trajectory.Then the triggering checking device stores the predicted states received from the controller.At the next time,the sensor measures the current states and check the conditions(13)and(14).Either(13)or(14)is satisfied,the states are sent to the controller and the problem(2)is solved,then the updated information is sent to its neighbors.Otherwise,this measurement is discarded,and the sensor waits for the next sampling.The control action input to the plant is still the predicted one at the last triggering time.Then move horizon to the next sampling time,and repeat the above process.

Remark 2:The triggering condition(13)or(14)is verified by theith agent based on its current states,the predicted ones,and its neighboring predicted states.It can be seen as a distributed triggering condition.And the local controller may not solve the optimal problem while the triggering condition in its neighbors is satisfied.

Remark 3:It can be observed that the threshold is varying with time goes on,and may increase in a prediction horizon from the triggered time sinceσai(t)is increasing butLA1(t)and the item about its neighboring states in the left side of inequality(14)decay with time goes on.However,it presents a decreasing trend due to the states gradually closing to the steady state.Here,the states threshold represents a tolerance to the maximal error of the predicted states while satisfying the stability condition.Therefore,triggering condition(13)or(14)is exactly the ways we expected,and can potentially save more computational and communication resources than the conditions in[17].Because an event is triggered only when the performance index exceeds its value at the last updating time in this work,it leads to fewer triggering times than that of strategy in[17]where transmission happens if the cost function does not decrease successively at each sampling instants.However,it may take more time to reach the desired point because of relaxing the monotonicity.

Remark 4:In the implementation,we assume that the neighboring predicted states1,...,N.

B.Improved Event-triggered MPC

Due to the accuracy of the predicted states decreases with the horizon length,an overlarge prediction horizon is unnecessary.Although the quickness is improved,MPC with a short prediction may cause in feasibility.It’s also noted that the optimal solution may be in feasible with the aforementioned eventtriggered MPC scheme because of constraints or disturbances.Considering these problems,we adopt the method with a series of asymptotically stable invariant ellipsoids in[19]to expand the feasible region.The difference is that we only optimize and minimize the terminal constrained set when the states are infeasible to the optimal problem(2),and the terminal penalty matricesPiis fixed.

Specifically,we first set a target terminal setand compute the maximal control invariant ellipsoid setboth Φiandsatisfy the Assumptions 3 and 4.Solve the following minimization problem to steer the terminal set valued state predictionintoThe state can always be controlled to the terminal set with this optimal problem if the initial state is feasible to Φi,see[19].Hence,the feasibility can be ensured all the time and feasible region is extended.

The triggering condition is designed similar as(13)and(14).And the whole control strategy for every subsystem can be described as Algorithm 1,taking theith subsystem for example.

Algorithm 1 Improved Event-triggered MPC

Remark 5:If controllers in the the subsystems are triggered synchronously,we adopt an iterative algorithm to realize agent negotiation.

Remark 6:The optimal problem(15)is solved only if there is no feasible solution to the problem(2)in this paper.If the problem(2)is replaced by the problem(15)with the same parameters in the implementation,the triggering times are less than that of using the problem(2),but the cost values are relatively larger.

C.Stability Analysis

In this section,the feasibility and stability analysis of the proposed control strategy is going to be given.To ensure that there exists a solution satisfying all the constraints when there is an event,the feasibility is provided.Then,it’s proven the closed-loop system is Lyapunov Stable.

Theorem 1:Consider the system described by(1),and suppose that Assumptions 1−6 hold,the control actions are generated by Algorithm 1 with triggering condition(13)and(14).We have that the system state converges to the terminal set in finite time as long as the initial state is feasible.

Proof:In this paper,a state predicted trajectory is evaluated after measuring the current state.And if the predicted states at the prediction horizonexceeds the terminal set,we solve the optimal problem(15).Then we can construct a feasible control sequence based on the optimal solution atk,see(3),so that the optimal terminal set becomes closer to the target one recursively.Therefore,the control action is always feasible.At the triggering timeri,the cost function isAt time instantri+l,based on the triggering condition(13)and(14),the cost value corresponding to the feasible input satisfiesThen we haveand the system converges to the terminal set in finite time.

D.Selection of the Parameters

There are lots of parameters in this algorithm that significantly affect the system performance.The guidance to their selection is provided in this part.

1)Parameters in the Optimal Problem:As well known,the prediction horizonNcan trade off the system stability and rapidity,and also act as the maximal triggering interval in this paper.Since the mentioned algorithm can improve the system performance than traditional MPC with a short prediction horizon,but the computation burden and complexity are not reduced ifNis larger.Hence,the prediction horizonNselected can’t be overlarge.The control horizon here is equal to the prediction horizon.Besides,the weighting matricesQi,Qij,Riare symmetric positive definite matrices.The greater the elements in these matrices,the smaller the corresponding optimal variables obtained.Thus these matrices can be chosen based on the practical demands.The matrixPiand the feedback control gainK fichosen should ensure that the Assumptions 3 and 4 hold,and can be obtained by means of linear matrix inequalities concept[20].

2)Parameters in the Assumptions 1−5:Firstly,σishows the region of the initial feasible set,andσifin the target terminal set represents the final convergence of the system.The smallerthe closer system state tends to the desired point.Detailedly,after choosing the target terminal set,we can obtainσiby using thei-step controllable set[21].Then,are computed by trial-and error method.The design parameterβiin the triggering condition is selected in(0,1).It has a significant influence on the trade-off between the system stability and communication rates.The condition(13)and(14)with a smallerβilead to more frequent communication,but the system performance obtained is better.

Fig.2. State trajectories with different strategies.(Let xi=[xi1;xi2].)

IV.SIMULATION

This section illustrates the performance of the proposed Algorithm 1 in simulation.Consider a discrete LTI system consisting of 3 agents with a cooperative objection,where the system matrices are as follows:

The state and control constraints areBased on the principles in Section III,the tuning parameters for each agent are set withN=5,Q1=Q2=Q3=I2,R1=R2=R3=I1,Q12=Q13=0.5I2,Q21=Q31=I2.To satisfy the Assumptions 3 and 4,we set1thenσ1=36,σ2=33,σ3=33,and the matricesPi,K i(i=1,2,3)are obtained.

The other parameters required are numerically found,such as,LQ1=67,LQ2=47,LQ3=47,Lf1=13,Lf2=

A.Simulation Results and Analysis

First,we execute the proposed Algorithm 1 at the feasible initial statesx1(0)=[0.5,0.5]T,x2(0)=[−1,−2]T,x3(0)=[0,3]Twith a small disturbanceswi,‖wi‖≤ 0.05,i=1,2,3.Then the states trajectories,cost function values and the triggering instants,shown in Figs.2−6,are compared with that of the traditional distributed MPC(DMPC)with an iterative scheme[1]and the event-based MPC in[17]for a linear distributed system.

As is shown in Fig.2,the optimal state trajectory with Algorithm 1 is well coincided with the trajectory under traditional DMPC,but there is a smaller deviation between the trajectory with strategy in[17]and the traditional DMPC.It’s observed from Fig.3 that the performance index decays slow ly,and even increases at the Steps 1 and 5 with Algorithm 1,while it decreases successively with the event-triggered MPC strategy in[17]and traditional DMPC.

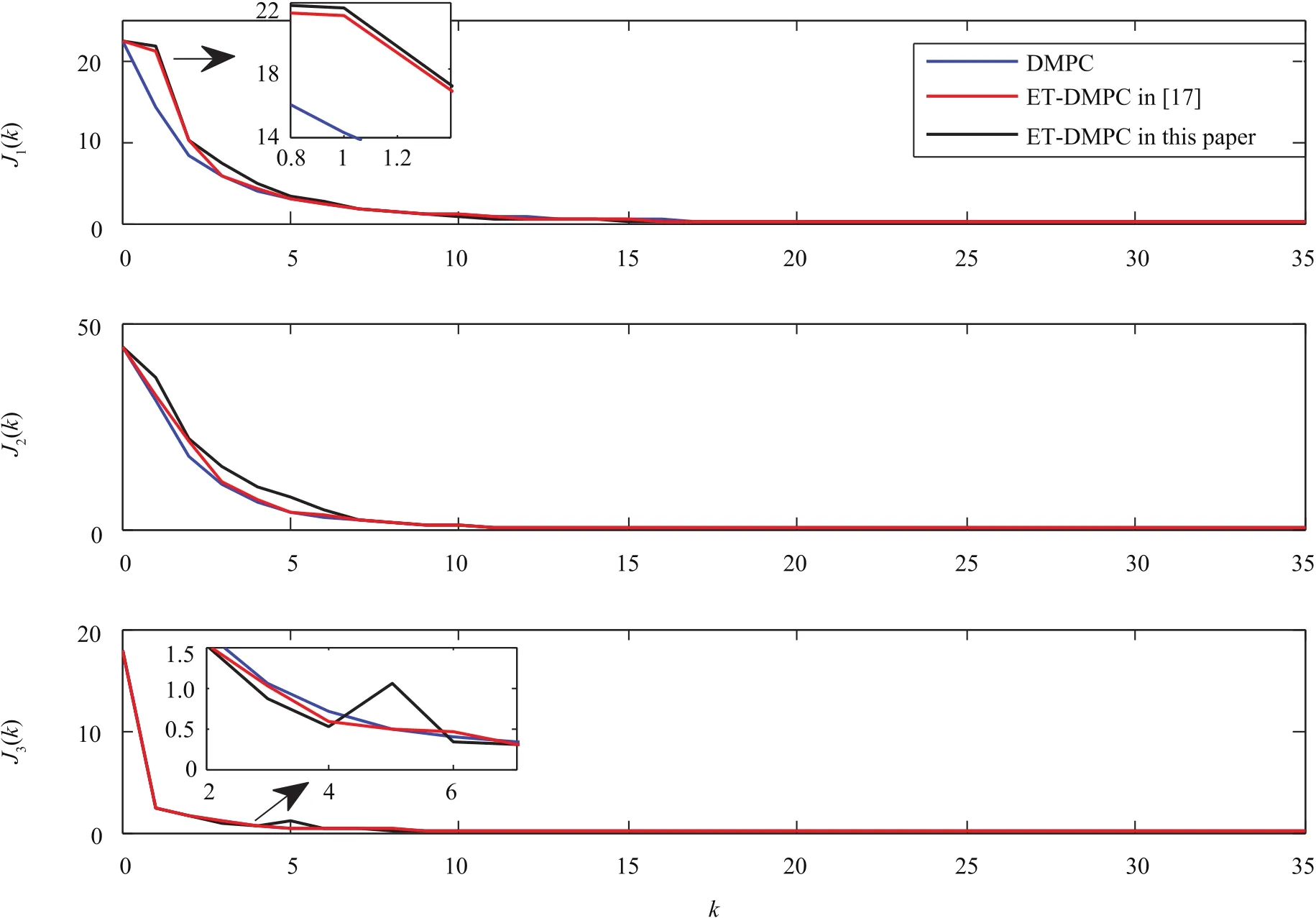
Fig.3. Cost function evolutions with different strategies.

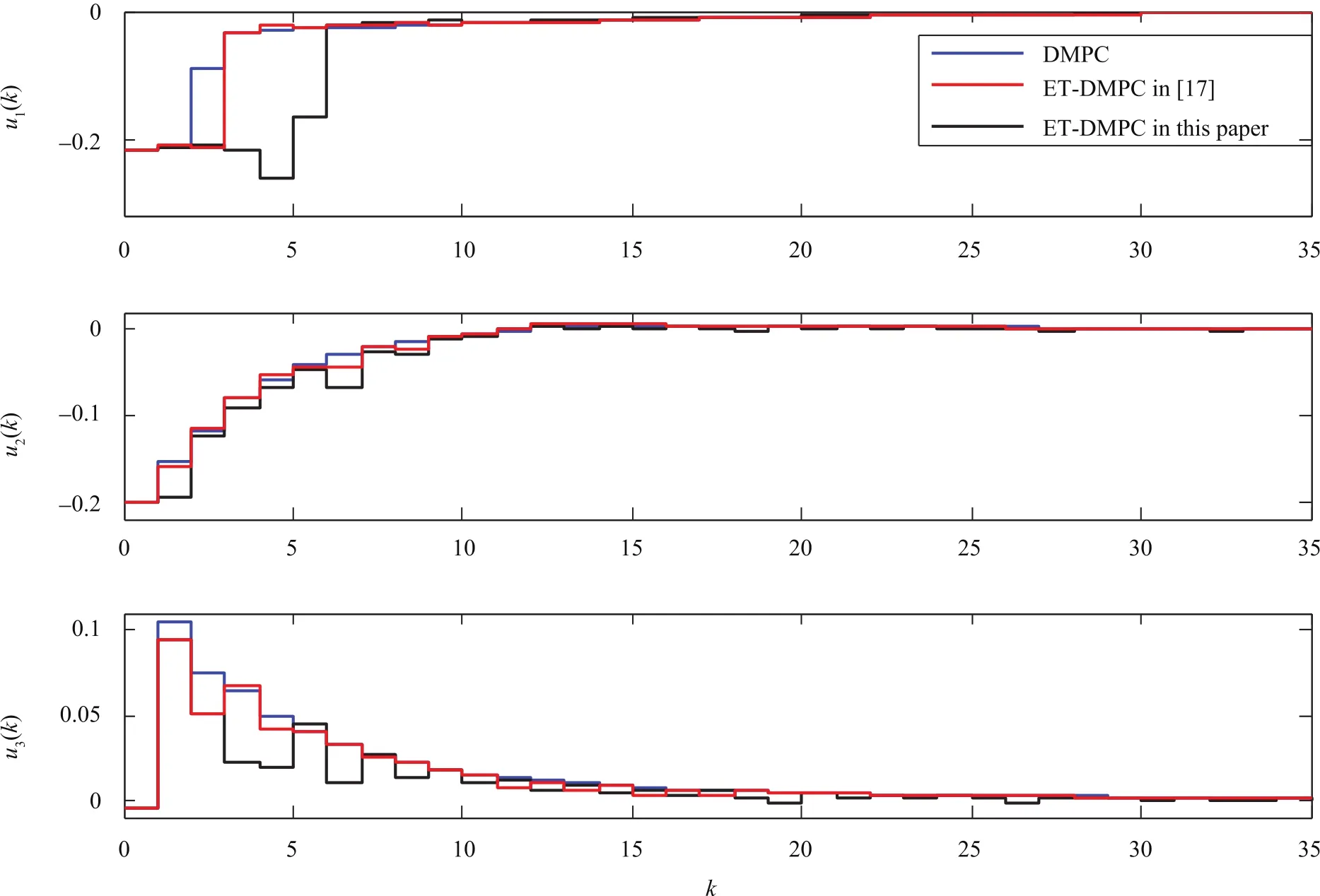
Fig.4.Control inputswith different strategies.

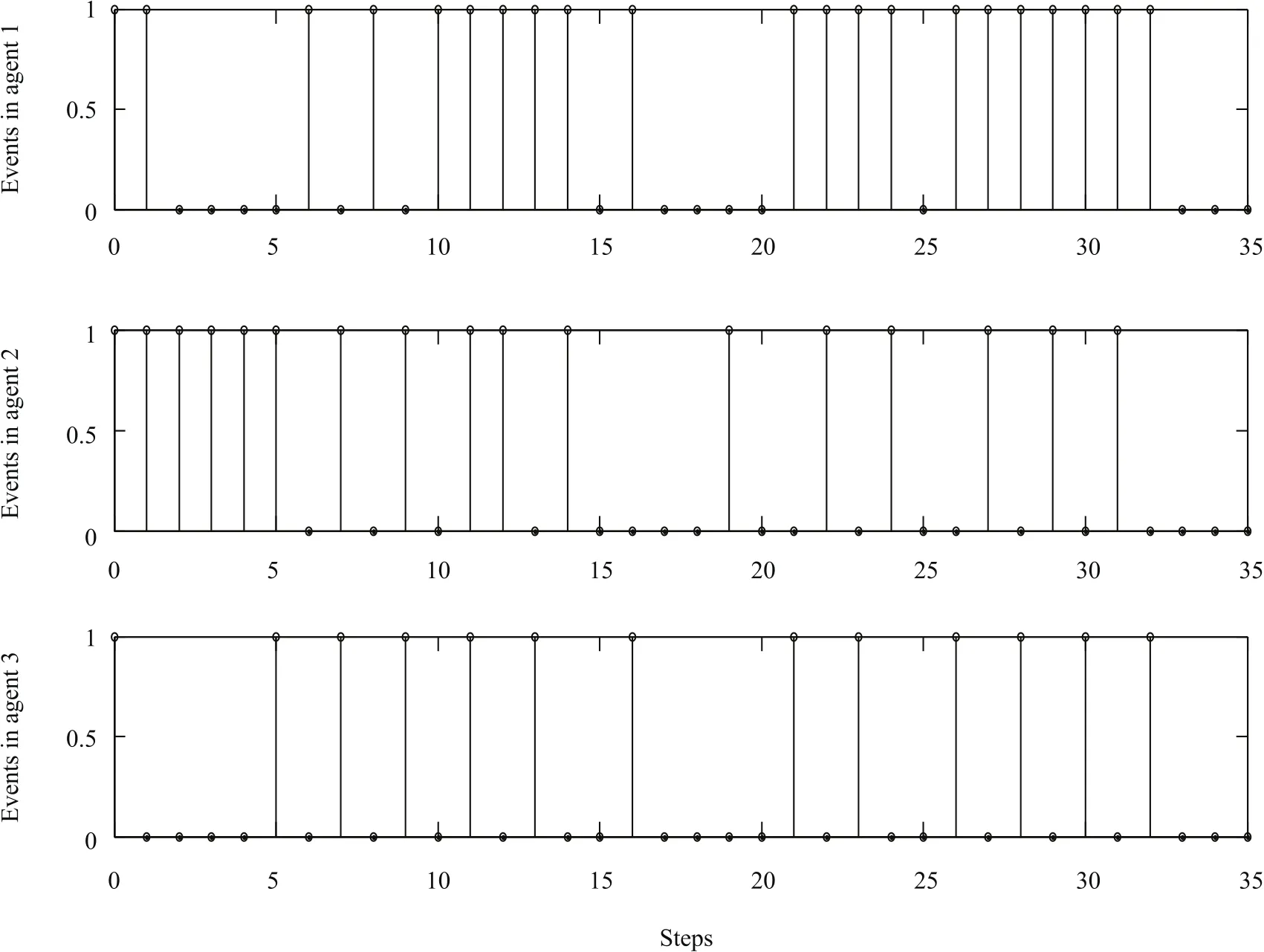
Fig.5.Triggering instants with Algorithm 1(x1(0)=[0.5,0.5]T,x2(0)=[−1,−2]T,x3(0)=[0,3]T,1–triggered,0–not triggered).

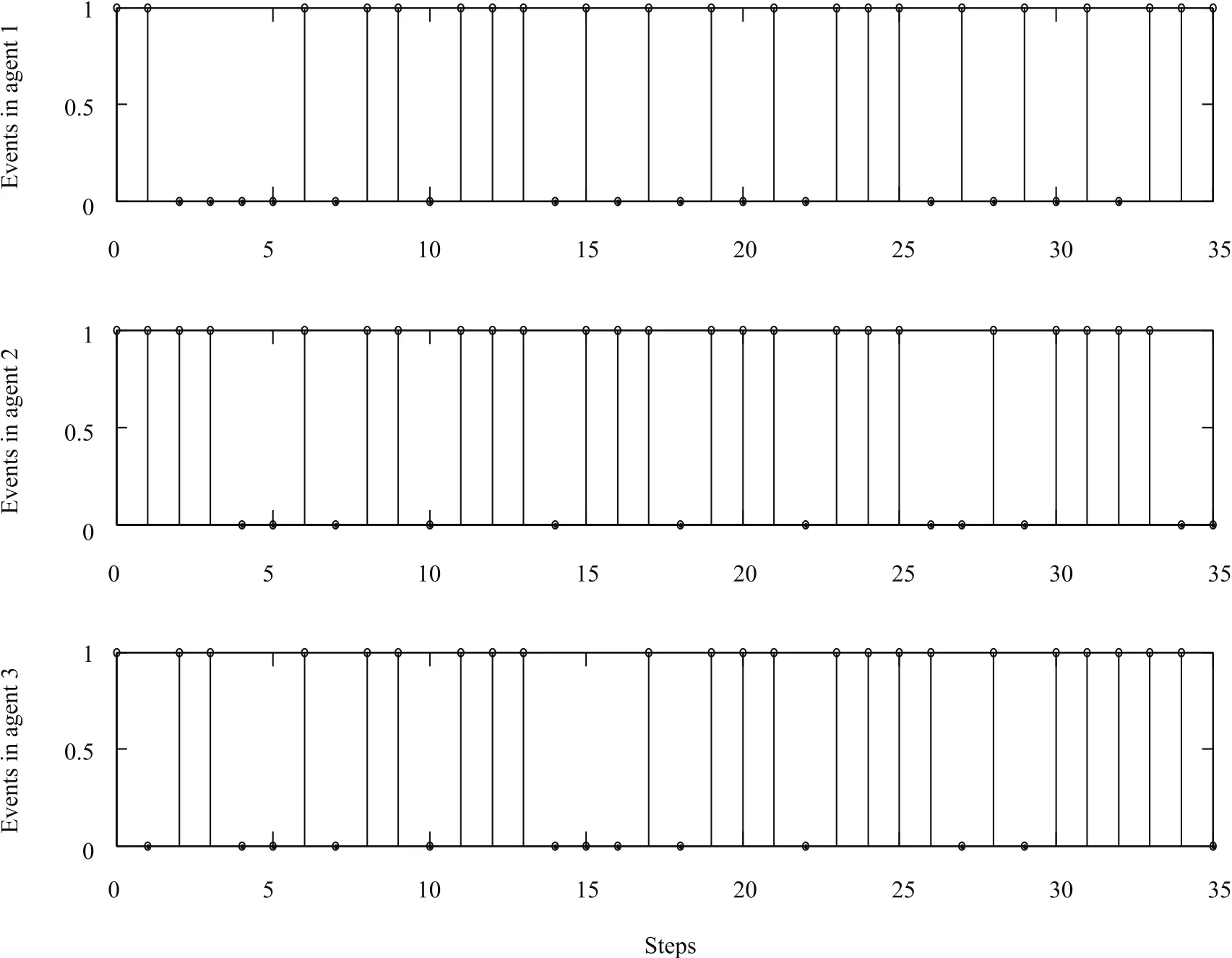
Fig.6. Triggering instants with strategy in[17](x1(0)=[0.5,0.5]T,x2(0)=[−1,−2]T,x3(0)=[0,3]T,1–triggered,0–not triggered).

In addition,in Figs.5,6,and 8,“1”denotes that an event occurs at this step,and the corresponding agents communicate with each other;otherwise, “0”shows that the triggering condition is not satisfied,and there is no communication between these agents.It’s easily observed that the less the number of “1”in Figs.5,6 and 8,the more communication resources saving.Contrasting Fig.5 with Fig.6,we can obtain that with the proposed Algorithm 1,the event between sensor and controller occurs 21 times in 35 simulation steps in the first agent,the number of events in the 2th agent and 3th agent are 17 and 13,respectively.We can get that with the event triggered MPC in[17],the controllers in the first agent,the 2th agent and 3th agent are triggered 21,24,23 times,respectively.Obviously,the triggering event happens less frequently than that of the event-triggered MPC in[17].Besides,in this paper,the controller in the first agent exchanges information with its neighbors 29 times,communication with neighbors for the 2th agent and 3th agent are 29 times and 23 times,respectively,while a tremendous amount of information is transmitted among these 3 agents caused by 102 times iterative calculation in the traditional DMPC.Hence,it saves more energy on computation and transmission over neighbors wireless network with Algorithm 1.

Therefore,the proposed method realizes a good trade-off between communication rate and the system performance.

Then,to illustrate the feasibility expansion with adaptive terminal set,we takex1(0)= [−1,−3]T,x2(0)=[1,−2]T,x3(0)= [0,−3]Tfor example,which is called infeasible states due to terminal constraints violation in the 1th agent.As shown in Fig.7,we get a series of minimal and optimal sets by solving the problem(15)at the time Steps 1,2,6 and 8,which are gradually narrow ing to the set terminal setXf.Finally,the agent states are steered to the desired position.Besides,the triggering instants are shown in Fig.8.It can be seen that the triggering condition(13)or(14)is always unsatisfied with the system gradually closing to the steady states,and it tends to control periodically whose period is equal to the prediction horizon.

In conclusion,the simulation results verify the effectiveness of the proposed Algorithm 1.

Remark 6:In Fig.7,“C1”represents the control invariant set Φ1in the first agent with the largest ellipse,“X f”denotes the target terminal set with the minimal one,the others are the optimal terminal sets solved by problem(15)at timek=1,2,6 and 8,when the optimal problem(2)is infeasible.After time 13,the terminal set keepsX f.

Fig.7. The adapting terminal set of the first agent with Algorithm 1.

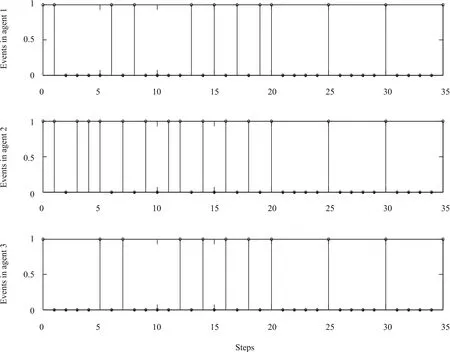
Fig.8. Triggering instants with Algorithm 1(x1(0)=[−1,−3]T,x2(0)=[1,−2]T,x3(0)=[0,−3]T,1–triggered,0–not triggered).

V.CONCLUSION

This paper presented an event-triggered MPC design algorithm for the distributed systems consisting of linear discrete time-invariant agents.We first described the basic event triggered MPC control strategy,then proposed a triggering condition based on the Lyapunov stability analysis intended to reduce the communication over wireless network largely.The condition proposed caused that the Lyapunov function non-monotonically declined,but was enforced not to exceed the value at the last triggered time.It’s different from the other method where the Lyapunov function decreased successively.Then the feasible region was expanded by adjusting the terminal set dynamically and the control algorithm based on these was given.Simulation results had validated the effectiveness of the proposed strategy.

The self-triggered scheme may be developed in the future study to reduce the idle states,and keep the nodes in sleep mode until transmission is required.And we will present different terminal criterion in the iterative algorithm using the event-triggered mechanism.

[1]R.Scattolini,“Architectures for distributed and hierarchical model predictive control-a review,”J.Process Control,vol.19,no.5,pp.723−731,May 2009.

[2]J.M.Maestre,D.M.De La Pe?na,E.F.Camacho,and T.A lamo,“Distributed model predictive control based on agent negotiation,”J.Process Control,vol.21,no.5,pp.685−697,Jun.2011.

[3]G.Anastasi,M.Conti,M.Di Francesco,and A.Passarella,“Energy conservation in wireless sensor networks:a survey,”Ad Hoc Networks,vol.7,no.3,pp.537−568,May 2009.

[4]W.P.M.H.Heemels,K.H.Johansson,and P.Tabuada,“An introduction to event-triggered and self-triggered control,”inProc.2012 IEEE 51st Annu.Conf.Decision and Control,Maui,USA,2012,pp.3270−3285.

[5]T.F.Liu and Z.P.Jiang,“A small-gain approach to robust event triggered control of nonlinear systems,”IEEE Trans.Automat.Control,vol.60,no.8,pp.2072−2085,Aug.2015.

[6]T.F.Liu and Z.P.Jiang,“Event-based control of nonlinear systems with partial state and output feedback,”Automatica,vol.53,pp.10−22,Mar.2015.

[7]T.M.P.GommansandW.P.M.H.Heemels,“Resource-aware MPC for constrained nonlinear systems:a self-triggered control approach,”Syst.Control Lett.,vol.79,pp.59−67,May 2015.

[8]W.P.M.H.Heemels and M.C.F.Donkers,“Model-based periodic event-triggered control for linear systems,”Automatica,vol.49,no.3,pp.698−711,Mar.2013.

[9]W.P.M.H.Heemels,M.C.F.Donkers,and A.R.Teel,“Periodic event triggered control for linear systems,”IEEE Trans.Automat.Control,vol.58,no.4,pp.847−861,Apr.2013.

[10]G.H.Wen,M.Z.Q.Chen,and X.H.Yu,“Event-triggered master slave synchronization with sampled-data communication,”IEEE Trans.Circuits Syst.II,vol.63,no.3,pp.304−308,Mar.2016.

[11]G.Guo,L.Ding,and Q.L.Han,“A distributed event-triggered transmission strategy for sampled-data consensus of multi-agent systems,”Automatica,vol.50,no.5,pp.1489−1496,May 2014.

[12]Y.Cheng and V.Ugrinovskii,“Event-triggered leader-following tracking control for multivariable multi-agent systems,”Automatica,vol.70,pp.204−210,Aug.2016.

[13]Y.Iino,T.Hatanaka,and M.Fujita,“Event-predictive control for energy saving of wireless networked control system,”inProc.American Control Conf.,St.Louis,USA,2009,pp.2236−2242.

[14]W.K.Wojsznis,T.Blevins,and M.J.Nixon,“Model predictive control with event driven operation,”inProc.2015 Int.Conf.Event-based Control,Communication,and Signal Processing,Krakow,Poland,2015,pp.1−6.

[15]D.Bernardini and A.Bemporad,“Energy-aware robust model predictive control based on noisy wireless sensors,”Automatica,vol.48,no.1,pp.36−44,Jan.2012.

[16]H.P.Li and Y.Shi,“Event-triggered robust model predictive control of continuous-time nonlinear systems,”Automatica,vol.50,no.5,pp.1507−1513,May 2014.

[17]K.Hashimoto,S.Adachi,and D.V.Dimarogonas,“Distributed aperiodic model predictive control for multi-agent systems,”IET Control Theory Appl.,vol.9,no.1,pp.10−20,Jan.2015.

[18]D. Groß, “Distributed model predictive control with event-based communication,”Ph.D.dissertation,Kassel Univ.Press GmbH,Kassel,2015.

[19]B.Pluymers,J.A.K.Suykens,and B.De Moor,“M in-max feedback MPC using a time-varying terminal constraint set and comments on‘Efficient robust constrained model predictive control with a time varying terminal constraint set’,”System&Control Letters,vol.54,no.12,pp.1143−1148,2005.

[20]D.V.Dimarogonas and K.J.Kyriakopoulos,”Event-triggered strategies for decentralized model predictive control”,inProceedings of the 18th IFAC World Congress,Milano,Italy:IEEE,2011,pp.10068-10073

[21]K.Hashimoto,S.Adachi,and D.V.Dimarogonas,“Distributed aperiodic model predictive control for multi-agent systems,”IET Control Theory&Applications,vol.9,no.1,pp.10−20,2015.