Distributed Containment Control of Networked Nonlinear Second-order Systems With Unknown Parameters

Long Ma,Haibo M in,Shicheng Wang,Yuan Liu,and Zhiguo Liu

I.INTRODUCTION

A San important branch of cooperative control,distributed containment control problem of networked systems has received special attention in recent years.Distributed containment control is a kind of leader-following type problem,in which multiple leaders construct a static or time varying shape in the space,named the convex hull,while the followers are forced to move within this region.As mentioned in[1],containment control is of interest for UAV cooperation control[2],robot swarms[3]and attitude control of rigid bodies[4],as a combination of formation and rendezvous problems.

The system models as well as the limitation of communication flow among the multiple dynamic leaders and the followers have attracted much attention for the containment control problem.For example,a distributed control algorithm is proposed in[5]which renders the followers to the convexhull spanned by multiple leaders under an undirected graph,which is extended in[6]−[8]to directed interaction graphs.The containment control problem for multi-agent systems is considered with transmission noises and switching topologies in[9],and with time delays in[10].However,they focus on first-order linear systems.Distributed containment problem in networks of second-order integrator kinematics is considered in[11],which is further extended by[12]and[13]to switching topology cases,by[14]to finite-time cases,by[15]to the system with homogenous dynamics,by[16]to time-varying delays and by[17],[18]to the case using only position measurements.In addition,[19]and[20]also present some theoretical results with sample-data based protocols.A ll these studies are more complicated than the case considering second-order integrator kinematics only.

Note that all the above references focus on linear systems with first-order and second-order linear dynamics.However,most of physical systems are inherently nonlinear[21]−[23],and recent studies pay more and more attention to nonlinear cases.For example,first-order nonlinear systems are considered in[24],[25]under undirected graphs and in[26],[27]under directed graphs.Reference[28]studies the second-order leader-following consensus problem of nonlinear multi-agent systems with only one single leader,while the authors in[29]present a distributed adaptive containment control approach for a group of uncertain flexible-joint robots with multiple dynamic leaders under a directed communication graph,and[30]considers the distributed containment control problem for networked Lagrangian systems in the presence of parametric uncertainties under a directed graph.Furthermore,reference[31]considers the distributed containment control problem of second-order multi-agent systems with inherent nonlinear dynamics,and proposes two distributed control protocols with static and adaptive control gains respectively.

In this paper,we study the containment control problem for a group of nonlinear second-order followers with multiple stationary/dynamic leaders in the presence of unknown parameters under directed graphs.Compared with[5]−[20]considering linear dynamics,this paper considers nonlinear dynamics.In contrast to[24]−[27]considering first-order nonlinear systems,this paper considers second-order nonlinear systems with unknown parameters.The contribution of this paper is twofold.First,we propose a control framework to drive the follower swith arbitrary initial states into the static/dynamic convex hull spanned by the multiple leaders under directed graphs.Second,in contrast with[30],we remove the requirement of the acceleration information by constructing a sliding mode estimator for each follower,and in contrast with[31],the controller in this paper does not need any global information about the whole communication topology,which is more practical and convenient in applications.

This paper is organized as follows.In Section II,we provide system models and graph theory,and some mathematical background information is presented.Main results on the regulation case and the dynamic tracking case for distributed containment control problem are provided in Section III.In Section IV,numerical examples are presented to illustrate the effectiveness of the proposed algorithms,and finally the results are summarized in Section V.

Notations:R:=(−∞,∞),R＞0:=(0,∞),R≥0:=[0,∞).λm{A}andλM{A}represent the minimum and maximum eigenvalues of matrixA,respectively.‖A‖2is the spectral norm of matrixA.|x|stands for the standard Euclidean norm for the vectorx∈Rn.For any functiontheL∞-norm is defined as,and theL2-norm as∫TheL∞andL2spaces are defined as the setsand{f:R≥0→Rn:‖f‖2＜∞},respectively.Re(·)denotes the real part of a complex number.

II.PRELIMINARIES

A.Dynamics of Agents

We consider a multi-agent system consisting ofnagents.Suppose that there existmfollowers,labeled as agents 1 tom,andn−m(n＞m)leaders labeled as agentsm+1 ton.The dynamics of themfollowers are described by

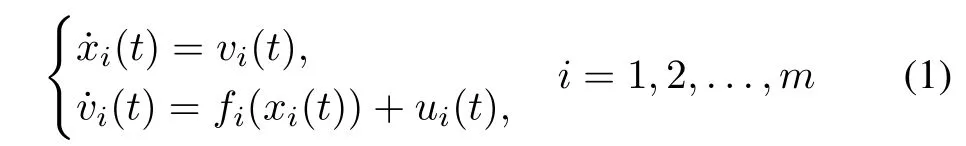
wherexi(t)∈Rpis the position state ofith agent,vi(t)∈Rpis the velocity state,ui(t)∈Rpis the control input,andf(xi(t))is the nonlinear dynamics of agenti,which is assumed to be unknown.Standard assumptions for existence of unique solutions are made,i.e.,f(xi(t))is continuous intand Lipschitz inxi(t),and can be parameterized as

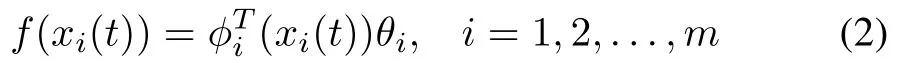
whereis a basic function matrix ofxi(t),which can be referred to as a regressor,and whenxi(t)is bounded,is bounded.θi∈Rpis an unknown constant parameter column vector to be estimated.

Remark 1:In this paper,the unknown nonlinear dynamicsf(xi(t))of all agents can be linearly parameterized as,which has been studied widely in classical adaptive control[32],[33].The practical examples of linearly parameterized model of multi-agent systems can also be found in[34],[35].

B.Graph Theory

Graphs can be conveniently used to represent the information flow between agents.LetG={V,ε,A}be an undirected graph or directed graph(digraph)of ordernwith the set of nodesthe set of edgesε⊆V×V,and a weighted adjacency matrixA={aij}with non-negative adjacency elementsaij.The node indices belong to a finite index setl={1,2,...,n}.An edge ofGis denoted byeij=(vi,vj)and it is said to be incoming with respect tovjand outgoing with respect tovi.For an undirected graph,∀i,j∈l,if(vi,vj)∈ε(G),then(vj,vi)∈ε(G),but it does not hold for a directed graph.A directed path from nodeito nodejis a sequence of edges of the form(i1,i2),(i2,i3),...,in a directed graph.A directed tree is a directed graph,where every node has exactly one parent except for one node,called the root,which has directed paths to every other node.A directed spanning tree of a directed graph is a direct tree that contains all nodes of the directed graph.A directed graph has a spanning tree if there exists a directed spanning tree as a subgraph of the directed graph.The set of neighbors of nodeviis the set of all nodes which point(communicate)tovi,denoted byThe graph adjacency matrixA=[aij],A∈Rn×n,is such thataij＞0 ifj∈N iandaij=0 otherwise.The in-degree of vertexviis denoted by∑Similarly,the out-degree ofviis denoted byIf the in-degree equals to the out degree for allvi∈V(G),then the graph is said to be balanced.D=diag[d1,...,dn]∈Rn×nis called the degree matrix ofG.The weighted Laplacian matrix ofGisL=D−A.

Lemma 1[6]:LetGbe a directed graph of ordernandL∈Rn×nbe the associated(non-symmetric)Laplacian matrix.The following three statements are equivalent:

1)The matrixLhas a single zero eigenvalue and all other eigenvalues have positive real parts;

2)Ghas a directed spanning tree;

For themfollowers andn−mleaders,we useVF={1,2,...,m}andto denote the follower set and the leader set respectively.LetxFandxLbe the column stack vectors ofxi(t),∀i∈VF,andxi(t),∀i∈VLrespectively.In this paper,we assume that the directed graphGsatisfies the following assumption.

Assumption 1:For each of themfollowers,there exists at least one leader that has a directed path to the follower.

C.Mathematical Background

Definition 2[37]:LetZn⊂Rn×ndenote the set of all square matrices of dimensionnwith non-positive off-diagonal entries.A matrixA∈Rn×nis said to be a nonsingularM-matrix ifA∈Znand all eigenvalues ofAhave positive real parts.

Lemma 2[37]:A matrixA∈Znis a nonsingularM-matrix if and only ifA−1exists and each entry ofA−1is nonnegative.

We assume that the leaders have no neighbors.Therefore,the(nonsymmetric)Laplacian matrixLassociated withAofGcan be written as

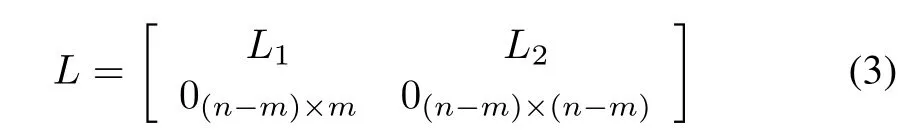
whereL1∈Rm×mandL2∈Rm×(n−m).

Lemma 3[30]:The matrixL1defined as in(3)is a nonsingularM-matrix if and only if Assumption 1 holds.In addition,if Assumption 1 holds,each entry ofis nonnegative and all row sums of−L−11L2equal to one.

III.ADAPTIVE CONTAINMENT PROTOCOL FOR MULTI-AGENT SYSTEM

In this section,we deal with the distributed containment control problem for networked nonlinear second-order systems with unknown parameters.Two cases are considered,i.e.,the case with stationary leaders,named regulation case,and the case with dynamic leaders,named dynamic tracking case respectively.Without loss of generality,we assume that the states and their first and second order derivatives of the leaders are given byj=m+1,...,nare supposed to be bounded.

A.Regulation Case

In order to achieve the goal of regulation containment control,the following condition has to be fulfilled:

whereCi∈Co(xL),xLis the vector of all the leaders’position state.

We give an auxiliary variable as follow

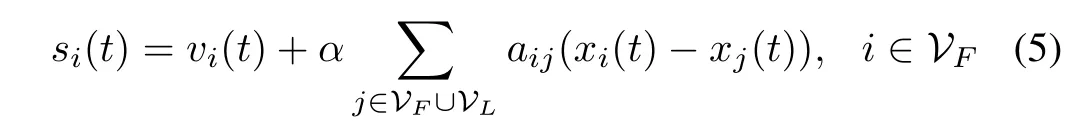
whereαis a positive constant.According to(1)and(5),we get that

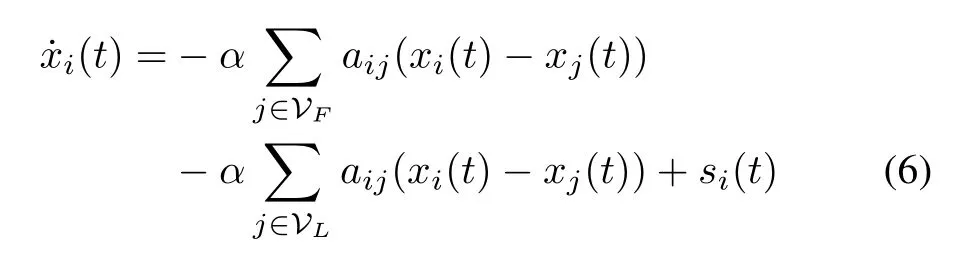
which can be written in a vector form as

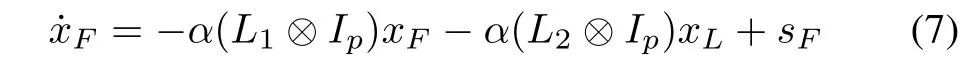
wherexFis defined above,sFis the vector ofsi(t),L1andL2are defined as in(3).

We design the input for theith follower as

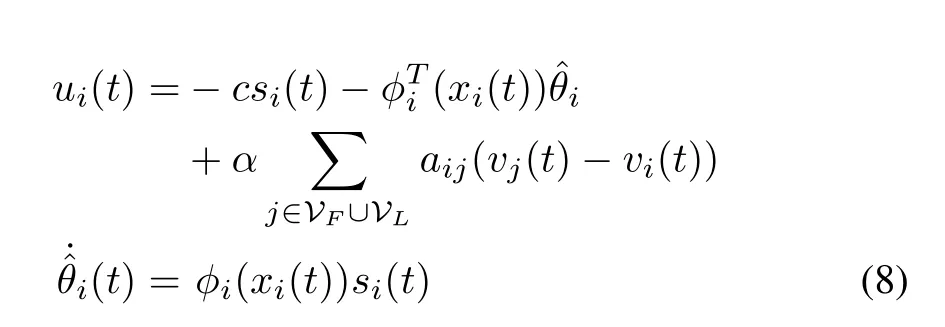
wherecisa positive constant,is the estimate ofis the derivative of,andis defined as in(2).

Remark 2:The auxiliary variablesi(t)is inspired by the sliding variable introduced in[21].The control algorithm(8)is designed to drive the variablesi(t)to zero.Then on the sliding surfacesi(t)=0,one can conclude that the followers converge to the convex hull spanned by the static leaders asymptotically.

Theorem 1:Using(8)for(1),the regulation case for arbitrary initial conditions in the presence of unknown parameters is achieved if and only if Assumption 1 holds.

Proof:(Sufficiency).By(1)and(8),the derivative ofsi(t)in(5)can be written as

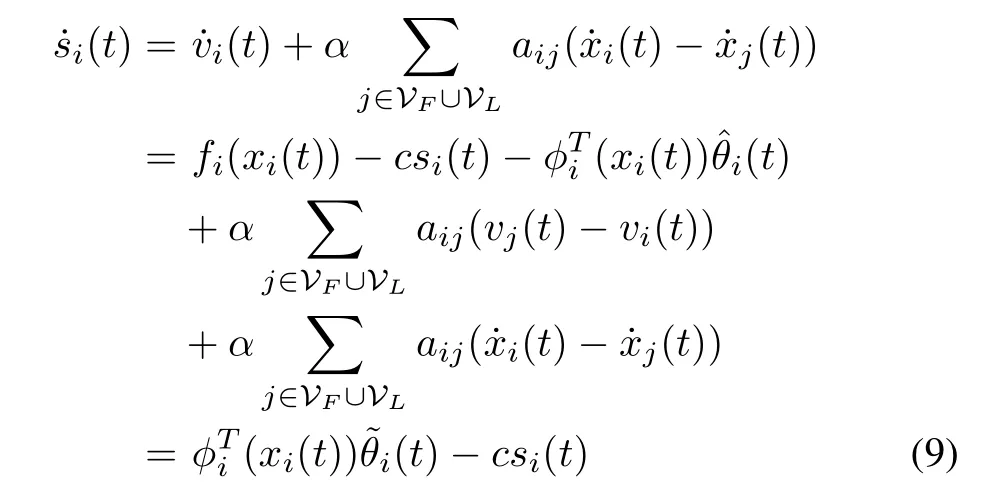
Define a positive semi-definite Lyapunov candidate functionV:C→R+for the system as

The derivative ofalong the trajectory of(9)is given by

Sinceandwe get thatsi(t)∈L∞Next,we show that.To achieve this,we only need to show that˙si(t)∈L∞according to Barbalat’s lemma[31].To this end,we rewrite(7)as

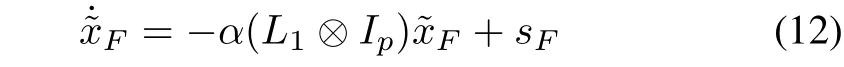
where

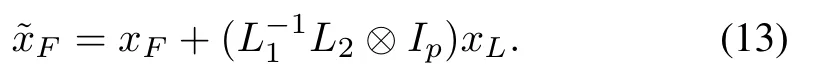
If Assumption 1 holds,we can get from Lemma 3 thatL1is a nonsingularM-matrix,and all eigenvalues ofL1have positive real parts,i.e.,all eigenvalues of−L1are in the open left half plane.On the other hand,the transfer function betweensFandof system(12)can be written as

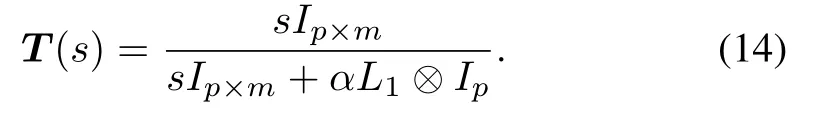
Note that the characteristic poles ofT(s)are just the eigenvalues of−αL1.Therefore,we conclude that the system(12)is stable.Sincesi(t)∈L∞,we haveand thus.Then we get thatandxF∈L∞,thusxi(t)∈L∞and,which implies thatBy differentiating(11),we can conclude thatis bounded.Therefore,˙V(t)is uniformly continuous in time.From Barbalat’s lemma,we can conclude thatasast→∞.In other words,ast→∞.

Next,we show that whensF→0mp,the control goal(4)is reached.Under Assumption 1,we get thatL1is a nonsingularM-matrix andL−11exists.It thus follows that whensF=0mp,(12)is globally exponentially stable at the origin.Therefore,it can be concluded that0mpast→∞.As a result,it follows from(13)and(12)thatandast→ ∞.If Assumption 2.1 holds,it follows from Lemma 3 that each entry ofis nonnegative and each row ofhas a sum equal to one.We then get from Definition 1 thatis within the convex hull spanned by the leaders.It follows that the control goal(5)is reached.This concludes the sufficiency part.

(Necessity).We prove the necessity part by contradiction.If Assumption 1 does not hold,there exists a subset of the followers which cannot receive any information from the leaders directly or indirectly.That is,the motions of these followers are independent of the states of the leaders.Therefore,these followers cannot always converge into the convex hull spanned by the leaders for arbitrary initial conditions.

B.Dynamic Tracking Case

In order to achieve the goal of containment control with dynamic tracking case,the following condition has to be fulfilled:

whereis the vector of all the leaders’velocity state.

DefineAs+1,...,nare bounded,we suppose that sup=1,...,m,v=1,...,p.Inspired by[38],we give the following lemma at first,where a distributed sliding-mode estimator is proposed to estimate the weighted average of the leaders’velocity.

Lemma 4:We design a distributed sliding-mode estimator for the follower agent as

withσi(0)=0 for each follower,,whereβ1andβ2are positive constants,andβ2＞γ,thenfor everyt＞T1,whereT1

Proof:Defineasi∈VF,and=0 asi∈VL,then it follows that(16)can be written as

wherei∈VF.DefineandThen the convergence time can be obtained by studying the following three cases:

Case 1:and.Whenit is trivial to show thatfor anyt＞0.Next we study the case whenandFrom(17)we get thatfor anyt＞0 becauseBy following a similar analysis,we can also get that,which means thatis nondecreasing.Note that whenwe get either.Next we show by contradiction that whenfor someonly happens at isolated time instants whent≤T.Assume thatfort∈[t1,t2]wheret1＜t2≤T.Then there exists some agent,labeled ask,with the statesatisfyingfort∈[t1,t3],wheret1Note thatimplies that∑fort∈[t1,t3]from(17).Ask(t)=it follows thatfort∈[t1,t3]implies thatfort∈[t1,t3].By following a similar analysis,it follows thafor,which results in a contradiction becausefort≤T.Therefore,whenwill keep increasing at a speed larger thatβ2−γwhent≤Texcept for some isolated time instants.It follows that the maximal convergence time is given by.Note that this bound also applies to the case when−(0)=0.

Case 2:andBy following a similar analysis toe 1,it can be computed that the maximal convergence time is given by

Case 3:andBy combining Case 1 and Case 2,it can be computed that the maximal convergence time is given by max

Combining the previous three cases completes the proof.Therefore,can be used to replaceσiwhent≥T1.

Remark 3:Finite-time convergence of the observer allows to design the observer and the control law separately,i.e.,the separation principle is satisfied[39].Therefore,it is allowed to design the sliding-mode estimatorin Lemma 4 and the control law separately.

We design another auxiliary variable as

wherei∈VF.Then(18)can be written in a vector form as

Then,the inputs of the followers are chosen as

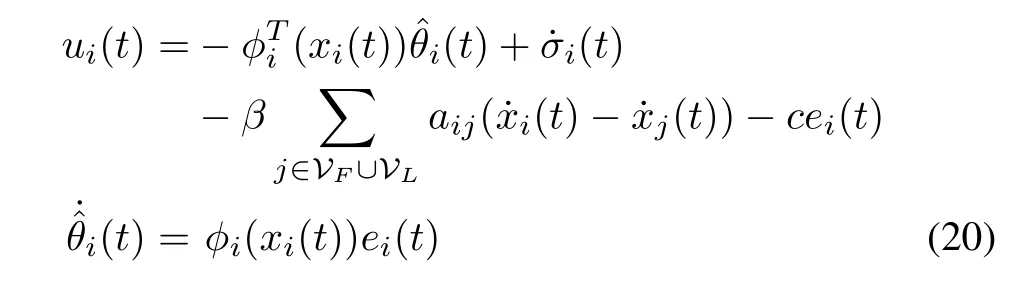
wherecis a positive constant,is the estimate ofθi,andis the derivative of

Theorem 2:Using(20)for(1),the dynamic tracking case for arbitrary initial conditions in the presence of unknown parameters is achieved if and only if Assumption 1 holds.

Proof:(Sufficiency).In the sense of(1)and(20),the derivative ofei(t)in(18)can be written as follow:

Define a positive semi-definite Lyapunov candidate functionV:C→R+for the system as

The derivative ofalong the trajectory of(21)is given by

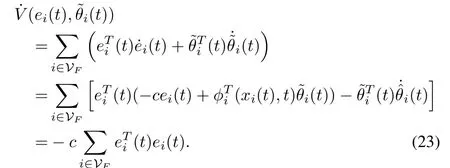
Similarly,we can conclude thatast→ ∞,i.e.,eF→0mpast→∞.From Lemma 4,we get thatcan be used to replaceσi(t)whencan be used to replaceσF,then(19)can be written as

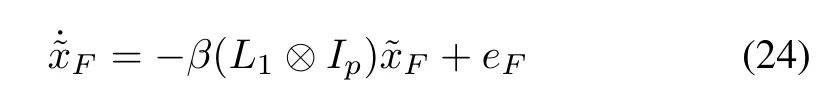
where

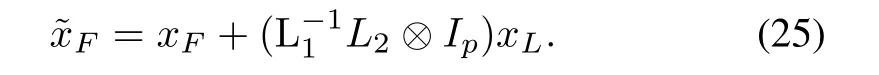
AsL1is a nonsingularM-matrix,it follows that wheneF=0mp,(24)is globally exponentially stable at the origin=0mp,andast→ ∞.As a result,it follows from(24)and(25)thatandast→∞.Therefore,the control goal(15)is reached.This concludes the sufficiency part.

(Necessity).The proof procedure is quite similar to the proof of Theorem 1,and we omit it due to space limitation.

Remark 4:Reference[31]also studies the distributed containment control problem of second-order multi-agent systems with inherent nonlinear dynamics,where two distributed control protocols are proposed.For the static control protocol,undirected and directed interaction topologies among the followers are taken into consideration.For the adaptive control protocol,it is proved that the containment control problem can be solved without requiring any global information if the interaction topology among the followers is undirected.Note that for directed interaction topologies,the controller in[31]needs some global information in the sense that each follower has to know the entire communication graph.However,the controllers in this paper relax this constraint,and apply to the containment control problem under directed graphs.

IV.NUMERICAL EXAMPLE

The unknown constant parameters are chosen here asθ1=[1 2]T,θ2=[2 1]T,θ3=[1 1]T,θ4=[2 2]T,θ5=[1 2]Tandθ6=[2 1]T,respectively.Allθiare set to be 10%−80%of accuracy of their real values.Fig.1 shows the directed graph that characterizes the interaction among the leaders and the followers.In our simulation,we chooseaij=1,i=1,...,6,j=1,...,10,if agentjis a neighbor of agenti,andaij=0 otherwise.For simplicity,the dynamics of the followers are assumed to be the same.

In the first case,we demonstrate the performance of the control law(8)for the regulation containment control problem.The initial positions of the six followers are set to be respectively,[−4,4]T,[0,6]T,[4,4]T,[−4,−4]T,[0,6]T,and[4,−4]T,and the initial velocities of the six followers are set to be respectively,[5,−1]T,[1,−3]T,[−12,−8]T,[10,3]T,[0,6]T,and[−7,0]T.The initial positions of the four stationary leaders are set to be respectively,[−2,2]T,[2,2]T,[−2,−2]T,and[2,−2]T.The control parameters are chosen asα=2 andc=2.

Fig.1.The directed graph that characterizes the interaction among the four leaders and the six followers,where Li,i=1,...,4 denotes the i th leader and Fi,i=1,...,6 denotes the i th follower.

Fig.2 shows the trajectories of the six followers when the leaders are static using(8).The black circles denote the four leaders,and the large black rectangle is the convex hull spanned by the leaders.The colorized squares denote the positions of the followers at respectively,t=0 s,andt=50 s.We see that the positions of the six followers converge to the convex hull spanned by the four leaders.Fig.3 shows one component of the velocities of the six followers using(8),and we get that the velocities of the six followers converge to zero asymptotically.

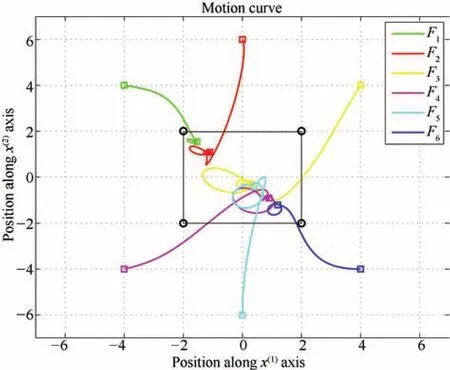
Fig.2.Trajectories of the six followers with four static leaders using(8).

In the second case,we demonstrate the performance of the control law(20)for the dynamic tracking containment control problem,and the four leaders are set to be dynamic.To better visualize the plot,we set the initial positions of the four leaders to be respectively,[6,8]T,[2,0]T,[6,4]T,and[2,4]T,and the initial velocities to be identical as[1,−2−8 cos(t)]T.Actually,the leaders can have different velocities,which means that the shape of the convex hull can be changing over time.The initial positions of the six followers are set to be respectively,[10,5]T,[5,10]T,[12,6]T,[6,12]T,[8,4]T,[4,8]T,and the initial velocities of the six followers are set to be respectively,[1,2]T,[2,1]T,[3,1]T,[1,3]T,[4,2]T,[2,4]T.The control parameters are chosen asβ1=2,β2=10,β=c=2.

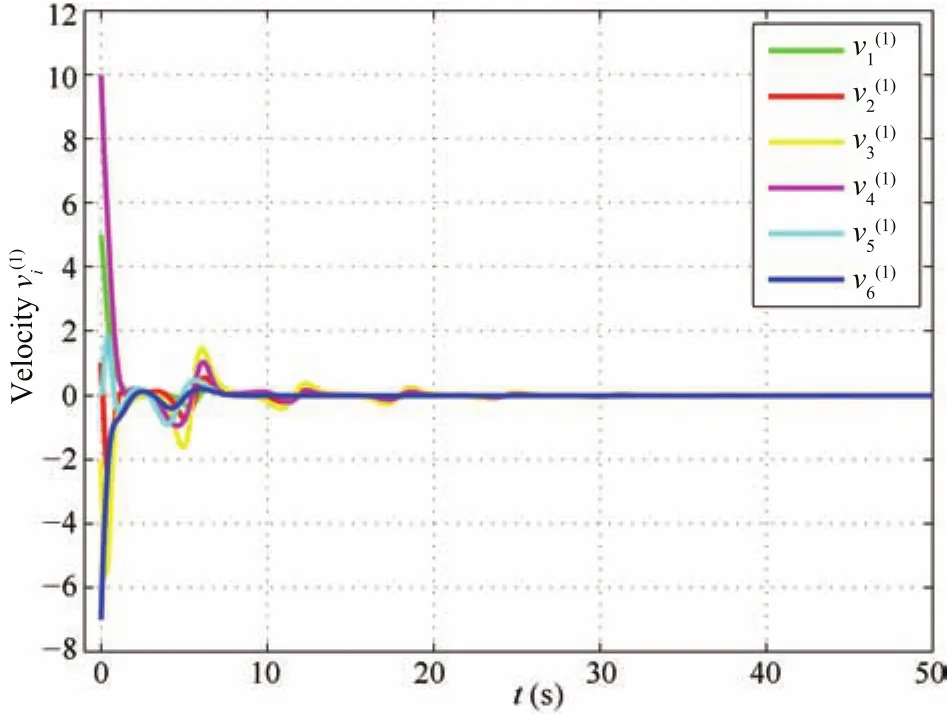
Fig.3. The velocityof the six followers using(8).

Fig.4 shows the trajectories of the six followers using control law(20)when the leaders move with varying velocities.The black circles denote the four leaders,and the black lines denote the trajectories of the four leaders,while the colorized lines are the trajectories of the followers.The colorized squares denote the positions of the followers at respectively,t=0s,t=8 s andt=18 s,and the black quadrangles denote the convex hull spanned by the leaders.We can see that the position states of the six followers not only converge into,but also move with the convex hull spanned by the four leaders.Fig.5 shows one component of the position containment errors of the six followers using(20),while Fig.6 shows one component of the velocity containment errors of the six followers.We can see that the position containment errors of the six followers converge to zero asymptotically,and the velocity containment errors of the six followers converge to zero,which means that the velocities of the six followers converge into the velocity convex hull spanned by the four leaders.From Fig.7,we can see that the sliding-mode vectorsσiconverge to the containment velocitiesvdiin finite time,just as what we demonstrate in Lemma 4.Moreover,there exists some vibration,named chattering effect,in Fig.7,which is inherent for the sliding mode algorithm.From Fig.8,we can see that the observation vectorseialso converge to zero asymptotically,just as what we demonstrate in Theorem 2.Remark 5:High frequency control switching leads to the socalled chattering effect which is exhibited by high frequency vibration of the controlled plant and can be dangerous in applications[40].To soften the inherent chattering problem,one can use the saturation function sat(·)to replace the sign function sgn(·),or use higher-order sliding modes[33].

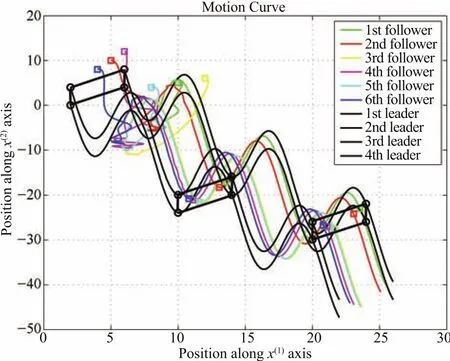
Fig.4.Trajectories of the followers with four dynamic leaders using(20).

Fig.5.The position containment errorsof the six followers with four dynamic leaders using(20).

Fig.6.The velocity containment errorsof the six followers with four dynamic leaders using(20).

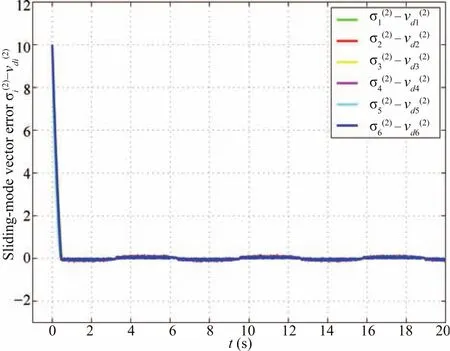
Fig.7.The sliding-mode vector errorsof the six followers with four dynamic leaders.

Fig.8. The observation vectorof the six followers with four dynamic leaders.

V.CONCLUSION

The distributed containment control problem for networked second-order nonlinear systems in the presence of unknown parameters has been studied in this paper.For containment problem with static leaders,we propose a distributed adaptive control algorithm combined with distributed observation vectors,and a necessary and sufficient condition is achieved.For the dynamic tracking case,we first introduce a distributed sliding mode estimator which guarantees the finite time convergence of the velocities to the convex hull,then a distributed adaptive control algorithm is proposed to render all the followers asymptotically converge to the convex hull spanned by the dynamic leaders.Future work involves the containment control for second-order nonlinear systems with time delay and switching topologies.

[1]L.Galbusera,G.Ferrari-Trecate,and R.Scattolini,“A hybrid model predictive control scheme for containment and distributed sensing in multi-agent systems,”Syst.Control Lett.,vol.62,pp.413−419,2013.

[2]J.Reimann and G.Vachtsevanos,“UAVs in urban operations:target interception and containment,”J.Intell.Robot.Syst.,vol.47,no.4,pp.383−396,Dec.2006.

[3]R.Haghighi and C.C.Cheah,“Multi-group coordination control for robots warms,”Automatica,vol.48,no.10,pp.2526−2534,Oct.2012.

[4]Z.Y.Meng,W.Ren,and Z.You,“Distributed finite-time attitude containment control for multiple rigid bodies,”Automatica,vol.46,no.12,pp.2092−2099,Dec.2010.

[5]M.Ji,G.Ferrari-Trecate,M.Egerstedt,and A.Buffa,“Containment control in mobile networks,”IEEE Trans.Automat.Control,vol.53,no.8,pp.1972−1975,Sept.2008.

[6]Y. C. Cao and W. Ren, “Containment control with multiple stationary or dynamic leaders under a directed interaction graph,”InProc.48th IEEE Conf.Decision and Control,Shanghai,China,2009,pp.3014−3019.

[7]H.Y.Liu,L.Cheng,M.Tan,and Z.G.Hou,“Containment control of continuous-time linear multi-agent systems with aperiodic sampling,”Automatica,vol.57,pp.78−84,Jul.2015.

[8]H.Haghshenas,M.A.Badamchizadeh,and M.Baradarannia,“Containment control of heterogeneous linear multi-agent systems,”Automatica,vol.54,pp.210−216,Apr.2015.

[9]S.Liu,L.H.Xie,and H.S.Zhang,“Mean square containment control of multi-agent systems with transmission noises,”Acta Automat.Sin.,vol.39,no.11,pp.1787−1795,Nov.2013.

[10]B.Li,Z.Q.Chen,Z.X.Liu,C.Y.Zhang,and Q.Zhang,“Containment control of multi-agent systems with fixed time-delays in fixed directed networks,”Neurocomputing,vol.173,pp.2069−2075,Jan.2016.

[11]Y.C.Cao,D.Stuart,W.Ren,and Z.Y.Meng,“Distributed containment control for multiple autonomous vehicles with double-integrator dynamics:algorithms and experiments,”IEEE Trans.Control Syst.Technol.,vol.19,no.4,pp.929−938,Jul.2011.

[12]Y.C.Lou and Y.G.Hong,“Target containment control of multi-agent systems with random switching interconnection topologies,”Automatica,vol.48,no.5,pp.879−885,May 2012.

[13]Y.C.Cao,W.Ren,and M.Egerstedt,“Distributed containment control with multiple stationary or dynamic leaders in fixed and switching directed networks,”Automatica,vol.48,no.8,pp.1586−1597,Aug.2012.

[14]Y.Zhao,Z.S.Duan,G.H.Wen,and Y.J.Zhang,“Distributed finite-time tracking control for multi-agent systems:an observer-based approach,”Syst.Control Lett.,vol.62,no.1,pp.22−28,Jan.2013.

[15]Y.S.Zheng and L.Wang,“Containment control of heterogeneous multiagent systems,”Int.J.Control,vol.87,no.1,pp.1−8,Jan.2014.

[16]K.E.Liu,G.M.Xie,and L.Wang,“Containment control for second order multi-agent systems with time-varying delays,”Syst.Control Lett.,vol.67,pp.24−31,May 2014.

[17]J.Z.Li,W.Ren,and S.Y.Xu,“Distributed containment control with multiple dynamic leaders for double-integrator dynamics using only position measurements,”IEEE Trans.Automat.Control,vol.57,no.6,pp.1553−1559,Jun.2012.

[18]B.J.Zheng and X.W.Mu,“Formation-containment control of second order multi-agent systems with only sampled position data,”Int.J.Syst.Sci.,vol.47,no.15,pp.3609−3618,Nov.2016.

[19]H.Y.Liu,G.M.Xie,and L.Wang,“Necessary and sufficient conditions for containment control of networked multi-agent systems,”Automatica,vol.48,no.7,pp.1415−1422,Jul.2012.

[20]J.Li,Z.H.Guan,R.Q.Liao,and D.X.Zhang,“Impulsive containment control for second-order networked multi-agent systems with sampled information,”Nonlin.Anal.:Hybrid Syst.,vol.12,pp.93−103,May 2014.

[21]J.J.Slotine and W.P.Li,Applied Nonlinear Control.Englewood Cliffs,New Jersey:Prentice Hall,1991.

[22]Z.K.Li,W.Ren,X.D.Liu,and M.Y.Fu,“Consensus of multi-agent systems with general linear and Lipschitz nonlinear dynamics using distributed adaptive protocols,”IEEE Trans.Automat.Control,vol.58,no.7,pp.1786−1791,Jul.2013.

[23]M.C.Fan,Z.Y.Chen,and H.T.Zhang,“Sem i-global consensus of nonlinear second-order multi-agent systems with measurement output feedback,”IEEE Trans.Automat.Control,vol.59,no.8,pp.2222−2227,Aug.2014.

[24]P.Wang and Y.M.Jia,“RobustH∞containment control for uncertain multi-agent systems with inherent nonlinear dynamics,”Int.J.Syst.Sci.,vol.47,no.5,pp.1073−1083,2016.

[25]H.Haghshenas,M.A.Badamchizadeh,and M.Baradarannia,“Adaptive containment control of nonlinear multi-agent systems with non-identical agents,”Int.J.Control,vol.88,no.8,pp.1586−1593,2015.

[26]X.W.Mu,Z.Yang,K.Liu,and J.R.Mu,“Containment control of general multi-agent systems with directed random switching topology,”J.Franklin Instit.,vol.352,no.10,pp.4067−4080,Oct.2015.

[27]H.Y.Liu,L.Cheng,M.Tan,Z.C.Hou,and Y.P.Wang,“Distributed exponential finite-time coordination of multi-agent systems:containment control and consensus,”Int.J.Control,vol.88,pp.237−247,2015.

[28]Q.Song,J.D.Cao,and W.W.Yu,“Second-order leader-following consensus of nonlinear multi-agent systems via pinning control,”Syst.Control Letters,vol.59,no.9,pp.553−562,Sept.2010.

[29]S.J.Yoo,“Distributed adaptive containment control of networked flexible-joint robots using neural networks,”Expert Syst.Appl.,vol.41,no.2,pp.470−477,Feb.2014.

[30]J.Mei,W.Ren,and G.F.Ma,“Distributed containment control for Lagrangian networks with parametric uncertainties under a directed graph,”Automatica,vol.48,no.4,pp.653−659,Apr.2012.

[31]P.Wang and Y.M.Jia,“Distributed containment control of second-order multi-agent systems with inherent non-linear dynamics,”IET Control Theor.Appl.,vol.8,no.4,pp.277−287,Mar.2014.

[32]R.Marino and P.Tomei,Nonlinear Control Design:Geometric,Adaptive and Robust.Englewood Cliffs,NJ:Prentice Hall,1995.

[33]S.Sastry and M.Bodson,Adaptive Control:Stability,Convergence,and Robustness.New Jersey:Prentice-Hall,1989.

[34]H.Bai,M.Arcak,and J.T.Wen,“Adaptive design for reference velocity recovery in motion coordination,”Syst.Control Lett.,vol.57,no.8,pp.602−610,Aug.2008.

[35]H.S.Su,G.R.Chen,X.F.Wang,and Z.L.Lin,“Adaptive second order consensus of networked mobile agents with nonlinear dynamics,”Automatica,vol.47,no.2,pp.368−375,Feb.2011.

[36]R.T.Rockafellar,Convex Analysis.New Jersey:Princeton University Press,1972.

[37]A.Berman and R.J.Plemmons,Nonnegative Matrices in the Mathematical Sciences.New York:Academic Press,Inc.,1979.

[38]Y.C.Cao,W.Ren,and Z.Y.Meng,“Decentralized finite-time sliding mode estimators and their applications in decentralized finite-time formation tracking,”Syst.Control Lett.,vol.59,pp.522−529,Sept.2010.

[39]J.Davila,L.Fridman,and A.Levant,“Second-order sliding-mode observer for mechanical systems,”IEEE Trans.Automat.Control,vol.50,no.11,pp.1785−1789,Nov.2005.

[40]A.Levant,“Higher-order sliding modes,differentiation and output feedback control,”Int.J.Control,vol.76,pp.924−941,Sept.2003.