Time-varying Algorithm for Swarm Robotics

Ligang Hou,Fangwen Fan,Jingyan Fu,and JinhuiWang

I.INTRODUCTION

SWARMING behavior is ubiquitous in nature,some species may be capable of achieving extremely complex tasks after their individuals form into swarm following certain orders,and as a result,benefit the migration,hunting,predators avoiding and nests building.The aggregation of individuals brings about quantity advantage,and in addition the intelligence displayed by the flock is far beyond what individual organisms possess,and it can be surprising even for humans.Such natural swarm system is formed with a strong robustness.Increasing or decreasing the number of individuals in a large scale will not affect its function and its self-organization ensure that the system will not break down due to the failure of any “core”.For such advantages,more and more researchers began to study and simulate the behavior of nature flocks,and attempted to copy their operating mode to the artificialintelligence system.In 1987,Reynolds[1]built a distributed behavioral model to simulate the behavior of a flock of birds,and proved that simple individual could achieve aggregate motion by dense interaction.This is the beginning of research on nature flock.In 1993,Beniet al.[2]suggested that cellular robotic systems were capable of “intelligent behavior”,and put forward the concept of swarm intelligence.After that,more and more algorithms for swarm robotics were proposed,typical cases include:Spectoret al.[3],[4]put forward SWARM and SWARMEVOLVE algorithms based on the work of Reynolds.Gaziet al.[5]−[7]used the artificial potential functions and the sliding-mode control technique to achieve swarm aggregation,formation and foraging based on the work of Khatib[8].Virághet al.[9]designed a flocking algorithm for autonomous flying robots.Reebs[10]tested the possibility of a minority of informed leaders leading a fish shoal to food,and later Couzinet al.[11]built a mathematical model to show how leadership affect s animal groups.Instead of proposing new algorithm,some researchers focused on the stability analysis[12]−[14],embedded systems are also involved to test or improving swarm algorithm[15]−[17].

With the rising attention on the swarm intelligence,research in this area kept developing,although the various algorithms described above have been able to achieve flexible motion control,but the invariable controller dominated algorithms usually have limited ability in practical situation.Once the controller is setup,it could not be changed until the task is overor the robot is reconfigured,and also sometimes they are unable to meet the changing environment.On the contrary,algorithm with variable controller is more suitable to describe the operating mode of swarm robot system in practical scenario and has a stronger adapt ability to environment:the variation of controller can be arranged along with the robots configuration so that the robot can complete a set of tasks without reconfiguration.Also the controller can be changed at any time if only the users issue relevant command to the robot,and the following actions of the robot will be dominated by new controller.Considering all these advantages and the fact that few researches focus on variable algorithm,this paper proposes a time-varying algorithm.The design of the algorithm and implementation details are discussed in Section II.Two models are built in Section III to establish the practical time-varying controllers and simulations are implemented to test actual control effect of the algorithm.A conclusion is drawn in Section IV.

II.ALGORITHM DESIGN

As mentioned previously,the aim of the algorithm is to make the controller contain time-varied elements,or make it a function of time,when the time changes the control function also changes.In addition,since the swarm may have division of labor and communication delay,it is allowed that each individual is to be driven by different functions at the same time to increase the flexibility of the algorithm.The implementation details are as follow:

Set up a swarm system composed ofMagents,letSjbe a set of control functions(suppose there areNfunctions in total),written as:

Arrange each member ofSjto act on the agentjrespectively duringIn order to express the control function at any timea function is created as shown below:

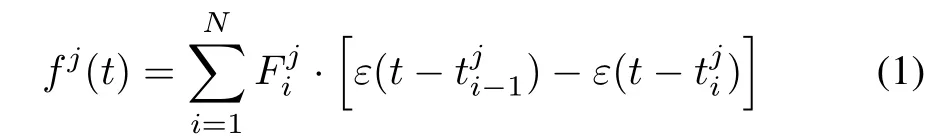
Take all the agents into consideration,there will be functionsrespectively acting on each agent.

Function shown above indicates that there is only one control function acting atany specific timet.Whentchanges from 0 tothe control function also changes fromto,and thus take turns dominating the motion of agent.There are plenty of control functions forflexible and time-varied control effect can be achieved by selecting proper functions to fill setSj.The control functions inSjcan be scheduled before the swarm system is activated.In addition,adding,removing or replacing functions during working process is also allowed.That means modification of the system can be made at any time to match the changing environment or tasks.

III.SIMULATION

In order to verify the control effect of the algorithm,two motion models are established and simulated separately based on the time-varying algorithm.

A.Simulation of Interaction Force Model

Supposing that all the agents interact with each other by exerting attractive force or repulsive force,agents can form into a stable formation when the force on each agent reaches a balance.Based on the R-A model[18],the interaction force model can be established as shown below:

whererepresents the resultant force on agentj,andis the magnitude of its horizontal and vertical components,is horizontal unit vector andis vertical unit vector,x,yare coordinates of agentj,xi,yirepresent coordinates of agentiwhich is around agentj(supposing there areKagents around agentj,then 0≤i≤K,i∈N).diis the distance between agentjand agenti,the interaction between the agents gets strengthened when distance between them decreases.ciis a proportionality coefficient related to the distance between agents,and reflects the direction and the strength of the interaction force,it is defined as follows:

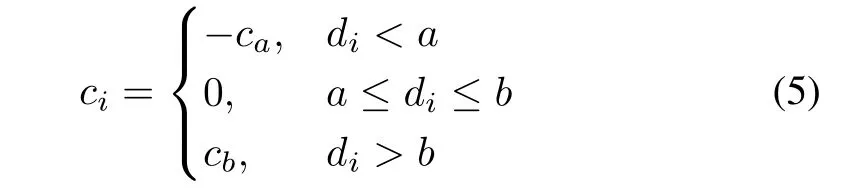
whereca,cbare always positive constants.The repulsive force dominates when the distance between two agents is less thana,andcishould be assigned a negative value in such condition;when the distance is larger thanabut less thanb,agents reach a state of balance,cishould be assigned 0;The attractive force dominates when the distance between two agents is larger thanb,andcishould be assigned a positive value.Differenta,b,ca,cbcan be selected to achieve different control effect,for variableb,the larger it is,the easier for agents to attract each other,and variableadetermines the tightness of the formation,smalleraleads to a tighter formation,ca,cbdetermines the magnitude of attractive force and repulsive force,they should be considered along with variableaandb.Fig.1 describes the interaction force model.

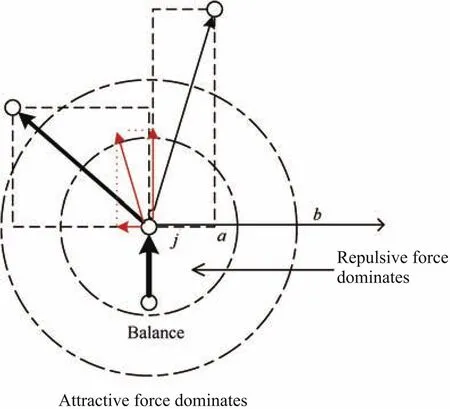
Fig.1.Interaction force model.

All the agents are respectively activated at random timeto bring them together,the control function of current state can be written as:

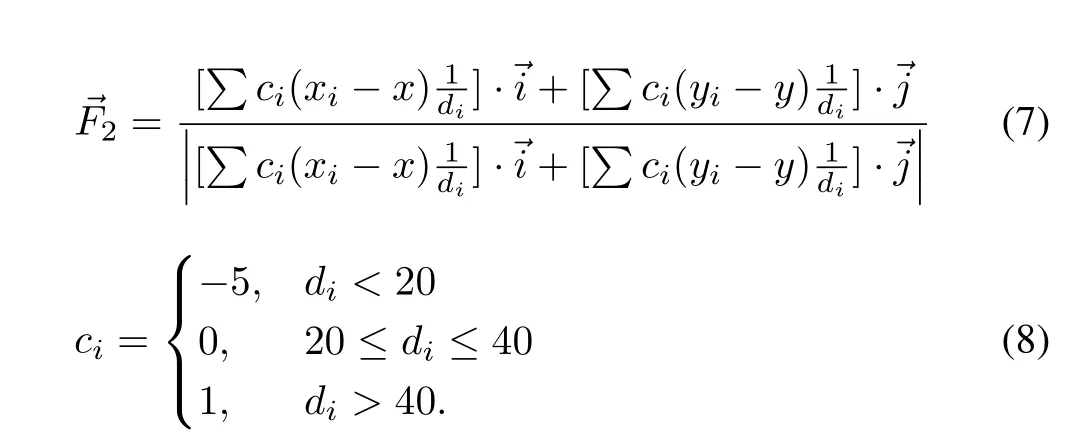
The values ofcimean that whendi＜20 the dominating force between two agents will be repulsive force.Whendiis greater than or equal to 40,agents will attract each other.Repulsive force is set stronger than attractive force to avoid collision.After gathering completes,all agents are made to spread orderly to form a new and looser formation,suppose such behavior begins at timet2and ends int3,then the control function can be written as

Considering all of the three stages,the control function of each controllable agent during the time period of[0,t3]can be expressed as

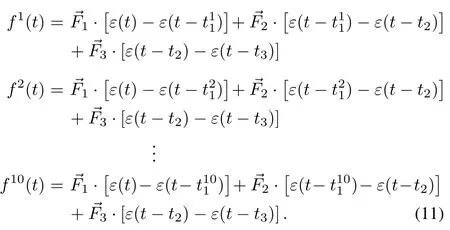
Carry out simulation based on the model described above,the results are shown in Fig.2.Fig.2(a)shows the changing of all agents’position through simulation time,the vertical axis represents time.Fig.2(b)shows the position of all the agents under the two steady states that are achieved by switching control function,and “+”in Fig.2(b)shows the initial position of agents.It can be seen in Fig.2(a)that all the agents remain static at beginning and their traces are vertically upward which means the position does not change with time.After activated sequentially they start to aggregate and after a period of time the gathering completes,a tight formation is formed as shown in Fig.2(b)with “*”.Subsequently,due to control function change,the agents disperse,and a looser formation appears,as the “o”in Fig.2(b)has shown.In the whole process the control function changed with time for three times,each time the agent took a new motion:remained stationary at first,formed a tight formation later and re-formed into a new formation at last.Each agent changes the state at different time which can be regarded as a simulation of the communication delay.

Fig.2.Simulation results.(a)Agents positions changing with time.(b)Two steady states achieved by switching control function.

B.Simulation of Target Oriented Model

The interaction forces model make the agents in the group gather in random positions which depend on the initial position of agents,and this position cannot be specified.In order to realize the directional movement of the group,the following model is considered:

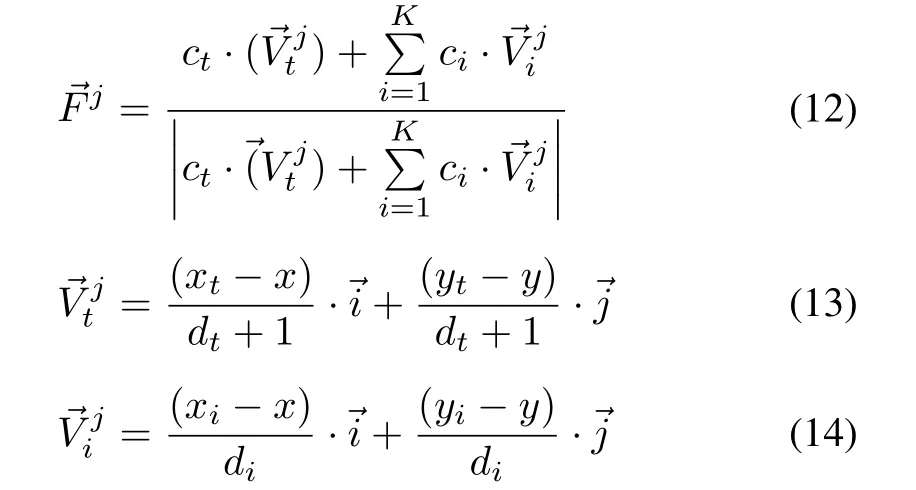
whererepresents resultant force of agentrepresents the vector from the agent to the target position,are the coordinates of target position anddtrepresents the distance between agentjand target position.Assume that there areKagents around agentj,and agentis one of theseKagents,thenrepresents the repulsive force between agentjand agenti.x,yrepresent the coordinates of agentj,xi,yirepresent the coordinates of agentianddiis the distance between agentiandj.ct,ciare proportional coefficients,ctshould be assigned a positive value andciis represented as follows:

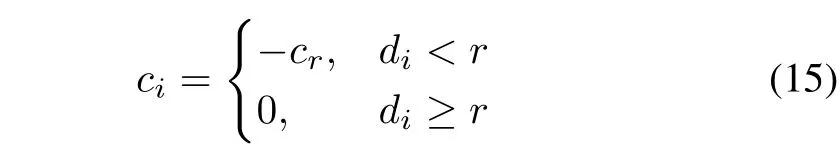
whererrepresents radius of repulsive force andcris a positive constant.This model is shown in Fig.3.

Fig.3.Target oriented model.

Assume that there are 20 agents with random initial positions,before they are activated at random timethe control function on each agent should be

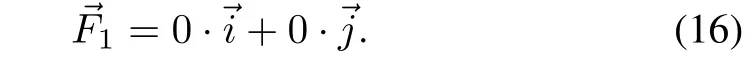
After the agents’activation,the target point can be set to the center of gravity of all agents to make them aggregate:

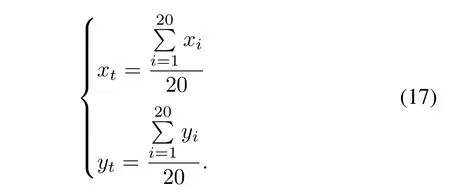
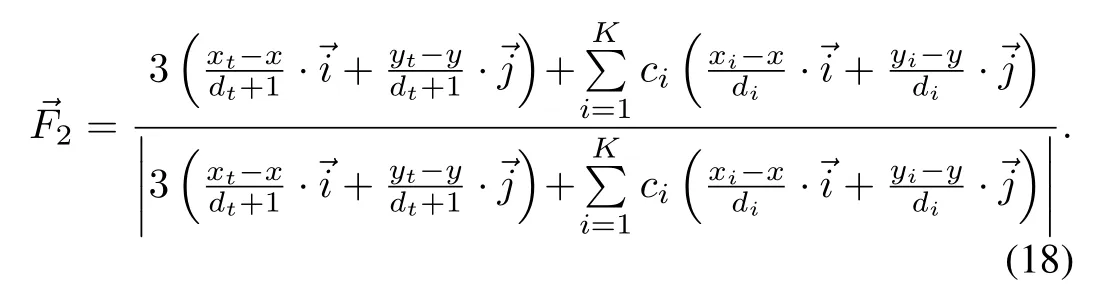
Later,two agents(for example agent 1 and 11)are chosen to be fixed att2.Meanwhile,the rest of the agents are divided into two groups,agents2,3,...,10 head to their target position(50,450),agents 12,13,...,20 head to(450,300).The control function on the fixed agents is

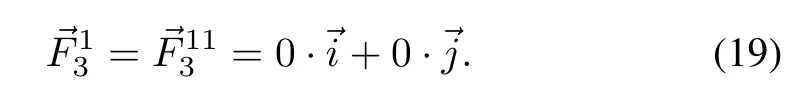
When the simulation is over att3,the control function of each agent within[0,t3]can be expressed as

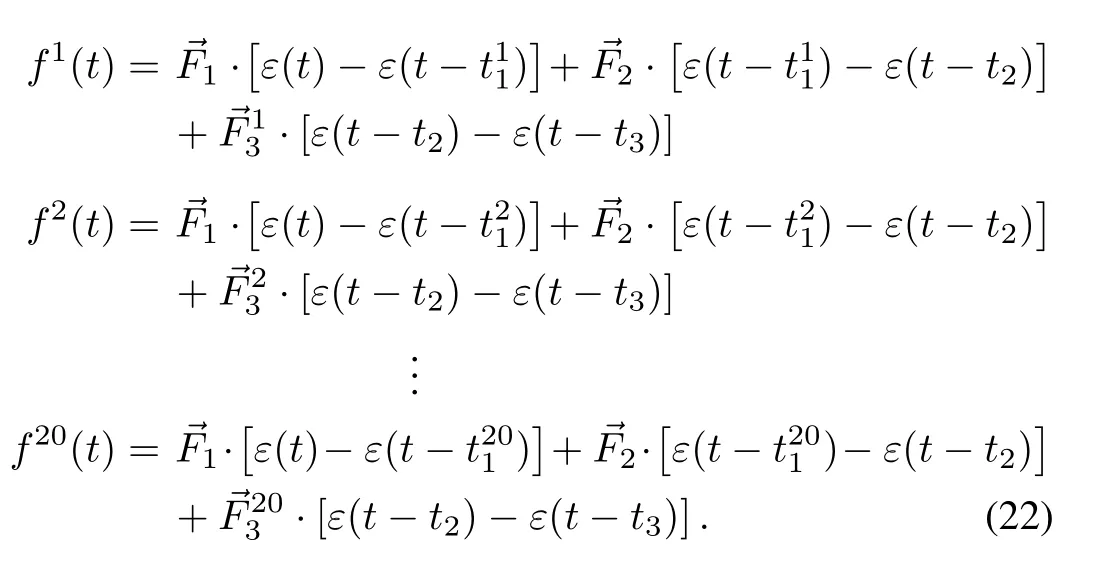
The simulation results are shown in Fig.4.All of the agents were initially static.When they were activated,they moved to the center of gravity position of all agents.After their arrival,a relatively stable state was achieved because of the balance between attractive force and repulsive force.In Fig.4(b),“*”marked the position of these agents.Later,the control functions on the agents changed,two agents(agent1 and agent 11)turned into stationary,and the rest of the agents are divided into two groups.They moved toward opposite side of the map.Because of the repulsive and attractive interaction between the agents,they could still maintain relatively stable formation and moved together without overcrowding or collision.Eventually two groups of agents arrived at the specified locations,which are shown as “o”in Fig.4(b).Fig.4(a)shows the changing of all agents position through simulation time.In the whole process,the control function of the population was changed for three times,each was stationary,directed aggregation and group division.Some agents in the third stage remain stationary to simulate the failure phenomenon of agents in a group.Due to the robustness of the cluster system,partial failure of the agents will not affect the group behavior.As shown in this simulation,although there are two agents which remain in place,the rest of the group can still finish the transfer and move unaffected.

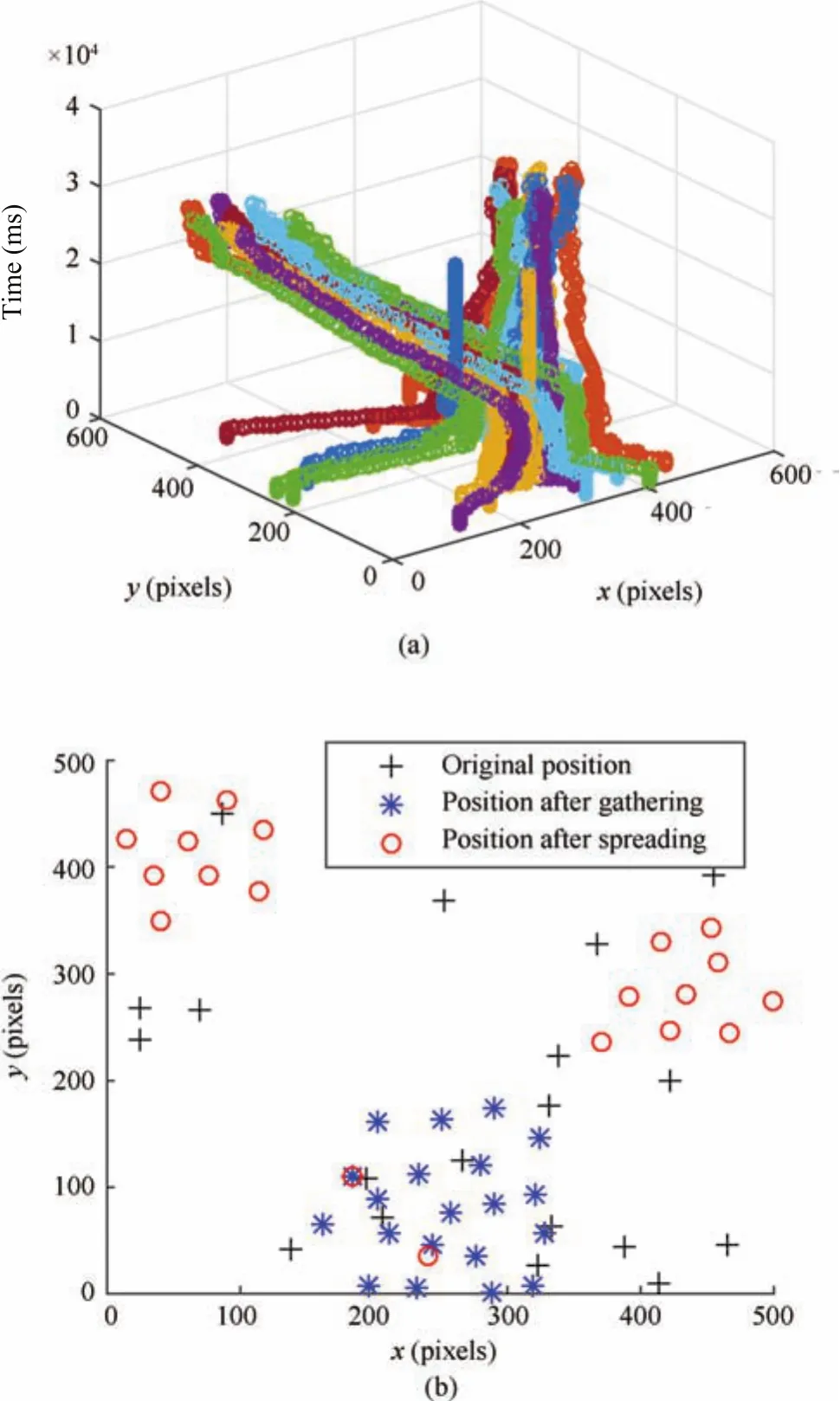
Fig.4.Simulation results.(a)Agents positions changing with time.(b)Two steady states achieved by switching control function.

IV.CONCLUSION

This paper discusses the limited ability of invariable controller dominated algorithms to control the swarm robot system,and hence a time-varying algorithm is proposed.Since the controller can be changed over time,the algorithm brings more flexible control effect.To test the actual effect of the algorithm,an interaction force model and a target oriented model are established,the controllers of the two models are put into the algorithm respectively and simulations are carried out.The simulation results show that the time-varying algorithm achieves not only aggregation,formation and directional movement as invariable controller dominated algorithms do,but also formation change,direction change,flock division and so on could be achieved by switching state during the simulation,which indicates that the time-varying algorithm is more flexible and practical,and makes the system be able to accomplish more complex assignment.The implementation of new hardware architecture,especially net based dynamic reconfigurable CPU that is suitable for this algorithm is our ongoing program.Unlike traditional architecture,the new one can be compiled on the net and is able to boot from net directly,therefore the system function can be modified in real time.Together with the time-varying algorithm,the performance of swarm intelligence can be improved to a great extent.

[1]C.W.Reynolds,“Flocks,herds and schools:a distributed behavioral model,”ACM SIGGRAPH Comput.Graph.,vol.21,no.4,pp.25−34,Jul.1987.

[2]G.Beniand J.Wang,“Swarm intelligence in cellular robotic systems,”inRobots and Biological Systems:Towards a New Bionics,P.Dario,G.Sandini,and P.Aebischer,Eds.Berlin Heidelberg,Germany:Springer,1993,pp.703−712.

[3]L.Spector and J.K lein,“Evolutionary dynamics discovered via visualization in the BREVE simulation environment,”Proc.8th Int.Conf.Simulation and Synthesis of Living Systems,Artificial Life VIII,Sydney,Australia,2002,pp.163−170.

[4]L.Spector,J.K lein,C.Perry,and M.Feinstein,“Emergence of collective behavior in evolving populations of flying agents,”Genet.Progr.Evol.Mach.,vol.6,no.1,pp.111−125,Mar.2005.

[5]V.Gaziand K.M.Passino,“Stability analysis of swarms,”IEEE Trans.Autom.Control,vol.48,no.4,pp.692−697,Apr.2003.

[6]V.Gaziand K.M.Passino,“A class of attractions/repulsion functions for stable swarm aggregations,”Int.J.Control,vol.77,no.18,pp.1567−1579,Jan.2004.

[7]V.Gazi,“Swarm aggregations using artificial potentials and sliding mode control,”IEEE Trans.Robot.,vol.21,no.6,pp.1208−1214,Dec.2005.

[8]O.Khatib,“Real-time obstacle avoidance for manipulators and mobile robots,”inProc.1985 IEEE Int.Conf.Robotics and Automation,St.Louis,MO,USA,1985,pp.396−404.

[9]C.Virágh,G.Vaśárhelyi,N.Tarcai,T.Szörényi,G.Somorjai,T.Nepusz,and T.Vicsek, “Flocking algorithm for autonomous flying robots,”Bioinsp.Biomimet.,vol.9,no.2,Article ID:025012,May2014.

[10]S.G.Reebs,“Can a minority of informed leaders determine the foraging movements of a fish shoal,”Anim.Behav.,vol.59,no.2,pp.403−409,Feb.2000.

[11]I.D.Couzin,J.Krause,N.R.Franks,and S.A.Levin,“Effective leadership and decision-making in animal groups on themove,”Nature,vol.433,no.7025,pp.513−516,Feb.2005.

[12]L.Yang,K.M.Passino,and M.Polycarpou,“Stability analysis of one dimensional asynchronous swarms,”IEEE Trans.Autom.Control,vol.48,no.10,pp.1848−1854,Oct.2003.

[13]N.Cai,J.X.Xi,and Y.S.Zhong,“Brief paper swarm stability of high order linear time-invariant swarm systems,”IET Control Theory Appl.,vol.5,no.2,pp.402−408,Jan.2011.

[14]I.I.Viksnin,A.L.Drannik,R.A.Iureva,and I.I.Komarov,“Flocking factors’assessment in case of destructive impact on swarm robotic systems,”inProc.2016 18th Conf.Open Innovations Association and Seminar on Information Security and Protection of Information Technology(FRUCT-ISPIT),St.Petersburg,Russia,2016,pp.357−363.

[15]M.Rubenstein,C.Ahler,and R.Nagpal,“Kilobot:a low cost scalable robot system for collective behaviors,”inProc.2012 IEEE Int.Conf.Robotics and Automation(ICRA),Saint Paul,MN,USA,2012,pp.3293−3298.

[16]J.Faigl,T.Krajník,J.Chudoba,L.P˘reuc˘il,and M.Saska,“Low cost embedded system for relative localization in robotic swarms,”inProc.2013 IEEE Int.Conf.Robotics and Automation(ICRA),Karlsruhe,Germany,2013,pp.993−998.

[17]B.Fidan,V.Gazi,S.H.Zhai,N.Cen,and E.Karatas¸, “Single-view distance-estimation-based formation control of robotic swarms,”IEEE Trans.Ind.Electron.,vol.60,no.12,pp.5781−5791,Dec.2013.

[18]I.D.Couzin,J.Krause,R.James,G.D.Ruxton,and N.R.Franks,“Collective memory and spatial sorting in animal groups,”J.Theoret.Biol.,vol.218,no.1,pp.1−11,Sep.2002.