Exploring Latent Semantic Information for Textual Emotion Recognition in Blog Articles

Xin Kang,Fuji Ren,Senior and Yunong Wu

I.INTRODUCTION

T HE recognition of human emotions for intelligent systems has been widely studied in many different fields.Recently reported studies include the affect analysis in human–computer interaction[1]−[3],the emotional traits examination in mental disease diagnosis[4]−[7],and the cognitive analysis of emotions in the neuroscience study[8],[9].Because emotions are the reflection of people’s mind states,perceiving emotions requires a deeper understanding of the semantic meanings in people’s behavior.In this paper,we explore the emotion recognition method based on natural language understanding,to fully understand human emotions expressed in the word-level and document-level texts.

Emotion recognition in natural language is a difficult study because human emotions are associated not only with the basic words but also with the context semantic meanings,which could even confuse the other human beings in many cases.For example,a positive word “happily”may express negative emotions in some specific contexts:Don’t bother me.I’m living happily ever after.A direct solution for recognizing such emotions m ight be constructing a dictionary[10]−[13]or a know ledge base[14],[15]for recognizing emotion expressions,or considering the semantic information in contexts such as the previous few words[10],[11]or the syntactically-related words[16],[17].However,models based on such dictionaries or know ledge bases suffer from a serious under-fitting problem,because the number of emotion triggering patterns grows exponentially large as the number of context words in consideration increases.Either building an emotion dictionary or training an emotion classifier would require a huge number of labeled examples,which could be too expensive to acquire in practice.

In this paper,we propose a novel method by exploring the latent semantic dimensions as the word context features,for learning the emotion expressions in natural language.Semantic dimensions are represented as the discrete random variables(or topics)in a Bayesian probabilistic model,each of which is associated with a word in the document.The model has to learn a distribution of the topic assignment for each word through a Bayesian inference by reading these documents,in which a distinct topic value can indicate a specific semantic dimension in the word context.In this process,each word can be associated with a series of topic assignments in a probabilistic distribution.The number of distinct topics is adjusted by fitting the Bayesian model fore motion recognition,but the size of increased feature space,which is linear to the distinct topic number,would be much smaller than the size of a dictionary or know ledge based feature space.Therefore,fitting an emotion recognition model based on our context semantic features would be much easier than fitting the model with traditional features.

We introduce two implementations of the Bayesian inference method for textual emotion recognition.The document and word emotion topic(DWET)model is a generative model,which infers the latent topics and the emotion assignments to words and documents by maximizing the probability of word generation throughout a corpus of documents.In the DWET model,we employ the two-level hierarchical conjugate probabilities to demonstrate the distributions of words,topics,and emotions throughout a corpus.The other hierarchical document and word emotion topic(HDWET)model is also a generative model.It shares the similar structural and probabilistic assumptions with the DWET model,except that a third level hierarchy is incorporated for the document-level emotion distribution in HDWET to allow a greater flexibility in the document emotion variation.By tuning the distribution parameters in these generative models,we generate the corpus level know ledge of emotion expressions with respect to the latent semantic dimensions in the context,and predict the emotion labels for words and documents to maximize the generative probabilities in these models.

The rest of this paper is arranged as follows:Section II reviews the related work in textual emotion recognition;Section III describes the construction and probabilistic assumptions in our Bayesian models for emotion recognition;Section IV illustrates the Bayesian inference method for learning the emotion expression know ledge and for predicting emotion labels in words and documents through a corpus;Section V details our experiment on textual emotion recognition,compares our results with the state-of-the-art emotion classification algorithms,and demonstrates the learned know ledge of emotion expressions with respect to different semantic dimensions;Section VI concludes this paper.

II.RELATED WORK

Developing the know ledge of emotion expression in natural language has been widely studied for textual emotion recognition.These studies include the emotion lexicon[18]generated on the co-occurrence of emoticon and emotion in blog articles,the emotion lexicon[11]selected from the Japanese evaluation expression dictionary[19]based on the emotion words proposed by Teramura[20],the emotion lexicon for verbs[12]which was manually annotated to the combination of a Dutch wordnet and a Dutch reference lexicon,and the emotion lexicon[13]based on the word-emotion association with crowdsourcing.Besides,there have been manually developed emotional rules such as the emotion lexicon and the lexical pattern based rules[11]for finding the emotion provoking events in the Web corpus,the manually developed rules[21]based on wordnet-affect[22]for constructing the groups of lyric emotions,and the application of common-sense know ledge such as the open m ind commonsense(OMCS)know ledge base[23]for the textual affect sensing[24],and the emotinet know ledge base for an emotion detection system[14].However,many studies on textual emotion recognition[25]−[27]suggested that the development of lexicons or know ledge bases for emotion expression in natural language could be very expensive,and serious accuracy problems could be caused in the developed know ledge base especially for the context sensitive emotion expressions.

There have also been studies on the extraction of context sensitive emotion information.Wuet al.[28],[29]employed a linear chain conditional random fields(CRF)model,based on the negative modifiers and the degree modifiers as context information in a sentence,for recognizing the emotions in words.Daset al.[30]also considered the context information such as the negative modifiers and punctuations in a sentence,and employed a CRF model for the word emotion prediction.

These recognized word emotions have been proved crucial for sentence and document emotion classifications.With an emotion lexicon learned through the statistical study of emoticons in online messages,Yanget al.[10]built a support vector machines(SVM)model and a CRF model respectively for the sentence and document emotion classifications in blog articles.Kanget al.[31]proposed a kernel-based method to investigate and compare different word-level emotion features for the sentence emotion prediction in a blog corpus.The major problem in these models is that the context features were either insufficient to demonstrate the sentiment information in natural language or dependent on a very large lexicon which causes the model difficult to fit.

Kanget al.[27]employed a sem i-supervised Bayesian framework to predict emotions in words,by incorporating the statistical relationship between words and emotion labels through the online micro-blog streams.By incorporating an emotion transition factor in the Bayesian framework,the model has successfully learned the author-specific emotion expression patterns in micro-blogs,and has effectively improved the emotion prediction accuracy in micro-blog documents.Other probabilistic models[32],[33]explored the word emotion and document emotion separately in blog articles,with emotion labels incorporated as a latent factor in determining the observation of words in the blog documents.Renet al.[4]examined the emotional traits in suicide blog streams with a probabilistic graphical model,and developed a suicide risk prediction system for the blog authors based on their writing histories with promising results.However,to our know ledge no study has explored the semantic dimensions in the context for simultaneously recognizing the textual emotions in words and documents.

III.BAYESIAN MODELS FOR EMOTION RECOGNITION

Bayesian models are the probabilistic description of observed values and hidden properties in the real world,in which observed values and hidden properties are represented as visible and latent variables respectively,with the influence among these values and properties represented as the directed connections between these variables.As a complete model of variables and their relationships,a Bayesian model defines the joint probability of all random variables with a directed acyclic diagram.Each random variable is associated with zero or more parent random variables based on some dependent and independent assumptions in the diagram.Probabilistic influence could flow through these directed connections in the diagram to allow probabilistic inference.The Bayesian models are convenient to describe such influence between different variables,because the joint probability of a Bayesian model is easy to factorize into the product of a series of conditional probabilities according to the Bayes’theorem,and each conditional probability could describe an influence from several parent variables to the child variable in the model.Each factorized probability would incorporate only a few random variables which are more suitable to be mathematically represented than the joint probability.In this paper,we propose two Bayesian models for emotion recognition in words and documents,as shown in Figs.1 and 2.The random variables,parameters,and indexes in these models are listed in Table I for the ease of illustration.

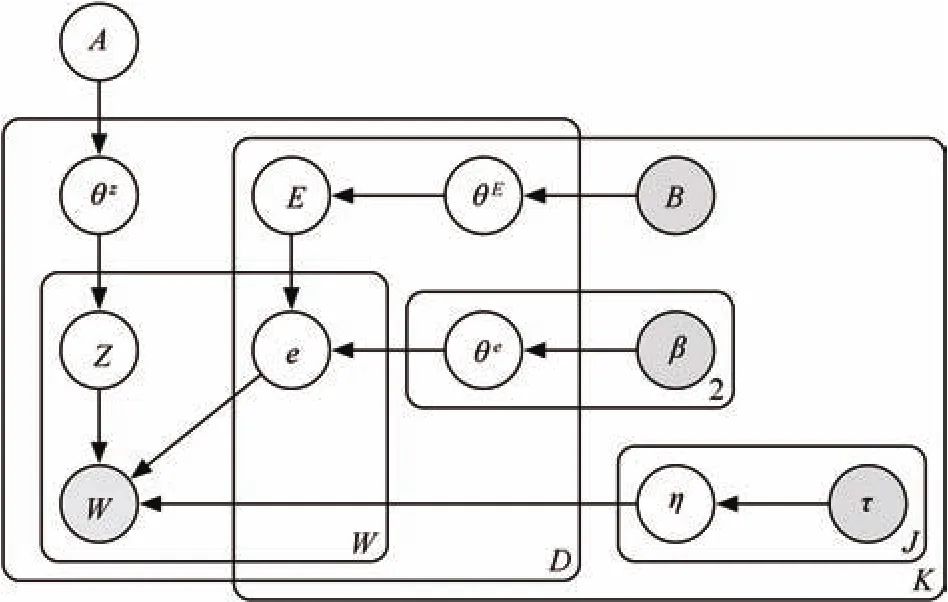
Fig.1.DWET model for predicting complex text emotions and emotiontopic variation.

Fig.2.HDWET model with corpus level emotion proportions for predicting complex text emotions and emotion-topic variation.

TABLE I INDEXES,RANDOM VARIABLES,AND PARAMETERS

A.Model Construction for DWET

The DWET model in Fig.1 describes a joint probability over the observed wordwdifor each document indexd∈{1,...,D}and each word indexi∈{1,...,Wd}throughout a corpus,the semantic dimension value(or topic)zdifor each word,the emotion labelsedikof each emotion categoryk∈{1,...,K}for each word,the emotion labelsEdkof each emotion category for each document,and variablesη,θz,θE,θe,A,B,β,τas the distribution parameters in the Bayesian model.

Besides,the DWET model describes a series of conditional probabilities over these random variables with directed connections as shown in Fig.1.The observation of a word inwdigiven its topic inzdiand corresponding emotions inedi·is assumed to follow a Categorical distribution

whereηzdiedi·is the proportional parameter in Categorical distribution.By arranging the topic variablezdiand the emotion variableedi·as parents to the word variablewdi,we construct a V-structurein which because the value of the child variablewis observed throughout the corpus,the assignments tozandefalls dependent on each other.This is because that the parent variables,which in the directed V-structure connections could jointly influence the value in the child variable,become inversely influenced by the observations in the child variable and any other parent variable through their posterior probabilities.This phenomenon is called “explaining away”in the Bayesian model.It allows the observation of a semantic dimensionzdi=jin wordwdito affect the distribution of word emotionsedi·through the posterior probabilityp(edi·|wdi,zdi),and therefore makes our emotion recognition depending on the semantic dimensions in the context.Compared to the lexicon-based,rule-based,and know ledge-based emotion inference,in which emotion distributions are represented asp(edi·|wdi,wdj,...),our DWET model significantly decreases the complexity in the conditional parts of the emotion probability.In fact,because the model describes a probabilistic connection between the wordwdiand topiczdivariables,we can interpret the context semantic information from a vector representation of the topic probabilities[p(zdi=1),p(zdi=2),...].

The topic variablezdispecifies a semantic dimension in the context of wordwdi.We incorporate totallyJsemantic dimensions in the DWET model,which correspond to a set of discrete valueszdi∈{1,2,...,J}for the topic assignment.A Categorical distribution is assumed for these discrete topic variables

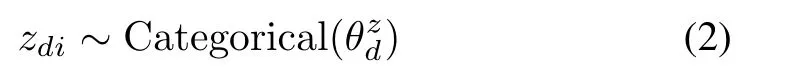
whereis the proportional parameter in the Categorical distribution with respect to a specific documentd.

The word emotion variableedik∈{0,1}specifies the existence of thekth emotion category inwdi,by taking binary values.We incorporate totallyKdistinct emotion categories,withk∈{1,...,K}indexing the specific categories.To analyze the influence of an emotion observation in a documentdto the emotion observations in corresponding wordswdi,we connect the document emotion variableEdkto the word emotion variablesedikin the DWET model,and assume Bernoulli distribution for the word emotion variable given a document emotion observation

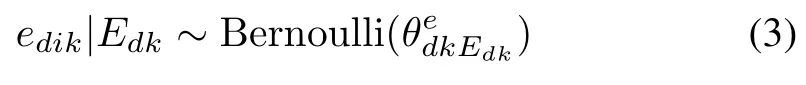
whereis the proportional parameter in the Bernoulli distribution with respect to documentd,emotion labelk,and the observation of document emotion inEdk.

The document emotion variableEdk∈{0,1}is also a binary random variable,which indicates the existence of thekth emotion category in documentd.Emotion categories and emotion indexes in documents are the same as those in words.We assume Bernoulli distribution for the document emotion variables

withas the proportional parameter for documentdand emotion labelk.Although the word emotion variablesed·kare absent in(4)for the document emotion distribution,the influence fromed·ktoEdkstill exists in our Bayesian model and is implemented through a Bayesian inference process.In fact,the probabilistic belief in document emotions would be rationally adjusted given the word emotion samples,as will be discussed later.

The DWET model assumption incorporates several proportional parameters inη,θz,θe,andθEas shown before.Although a direct optimization to these proportional parameters,through Bayesian inference,is feasible for training a model for the document and word emotion predictions,except that the learned values in these parameters might only fit well in the training process but could not adjust properly to new text samples in the real world.One of the advantages in building a Bayesian model is that we can represent the model parameters as random variables and make further assumptions on their distributions.This allows the model to adjust these parameters better,with more flexibility and better robustness in Bayesian inference,for recognizing emotions in the real-world texts.In the DWET model,we assume conjugate priors of the Categorical and Bernoulli likelihoods as the prior probabilities for these proportional parameters,which will simplify the derivation of their posterior probabilities in our Bayesian inference.

Specifically,for the proportional parameterηjkin(1),we assume Dirichlet distribution

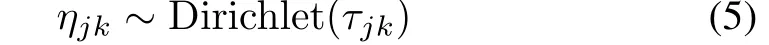
as its prior probability,which is also the conjugate prior of its Categorical likelihood function.τjkis the concentration parameter of this Dirichlet distribution,andj,kare the indexes of topic and emotion in wordwdi,respectively.For the proportional parameterin(2),we also assume the Dirichlet distribution as its prior probability,which is the conjugate prior of its Categorical likelihood function

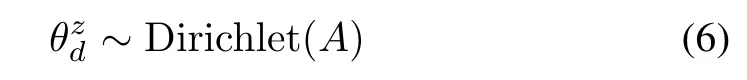
Ais the concentration parameter of this Dirichlet distribution.

Dirichlet distribution is used to describe the probability of probability mass assignments in the proportional parameters,likein(6).The proportional parametercan be specified as a set ofJprobability mass assignments1,...,J},in which each entrevaluates the probability of observing a topic value inzdi=j,by satisfying the following restrictions

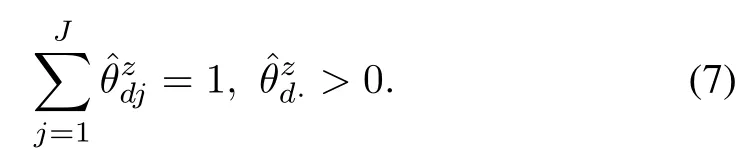
The Dirichlet distribution in(6)describes a probability density function for the continuous random variablesIt allows ato concentrate on a larger probability mass assignment with a larger concentration parameterAj,while restricting the probability mass assignments under(7).

For the proportional parameterin(3),we assume Beta distribution

as its prior probability,which is also the conjugate prior of its Bernoulli likelihood function.βkEdkis the concentration parameter in this Beta distribution,whileEdkcorresponds to the assignment to the document emotionEdk∈{0,1}with the same document indexdand emotion categoryk.Similarly,for the proportional parameterin(4),we also assume the Beta distribution as its prior probability,which is the conjugate prior of its Bernoulli likelihood functionBkis the concentration parameter in this Beta distribution.

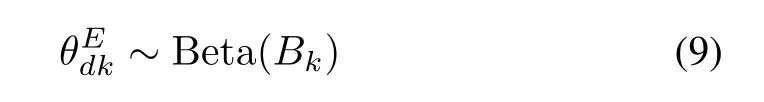
A Beta distribution can be considered as a simple Dirichlet distribution for the binary probability mass assignments.For example,the proportional parameterin(4)can be specified with the probability mass assignments ofin which

The Beta distribution in(9)describes a probability density function for the continuous random variable.It allowsto concentrate on a larger probability mass assignment with a larger concentration parameterBk,and restrict the probability mass assignments under(10).

B.Model Construction for HDWET

The HDWET model in Fig.2 describes a similar probabilistic model as DWET,except that we have relaxed the assumption for the document emotion concentration parameter to be constant by incorporating a random variableφkon the corpus-level and by employingαφkin

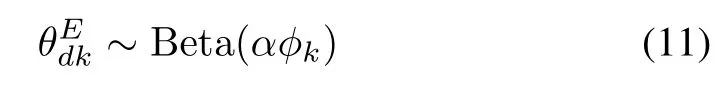
as a flexible document emotion concentration parameter.αis a constant hyper-parameter in(11).Becauseφis incorporated in the hierarchy of document emotion distribution,we name it the Hierarchical Document and Word Emotion Topic model.

In the previous DWET model,because the corpus-level concentration parameterBkis constant,all the document emotion proportional parametersfor differentdmust have the same probability densities as shown in(9).This corresponds to an implicit assumption that for each emotion categoryk,the model assumes the same prior probability to observe it in different documents.However,in the real text because the probabilistic concentration of document emotion varies dramatically through different documents,the model needs to adjust itself to all kinds of emotion distributions to properly recognize these document emotions.In the HDWET model,we incorporate the variability in document emotion distribution with a corpus-level concentration parameterαφk,as shown in(11).

We assume Beta distribution for the document emotion concentration parameterφk

inwhichBkonly poses a prior assumption on the emotion distribution and does not directly influence the probabilistic distribution for document-level emotions.As a constant parameter,Bis initialized by counting the observation of document emotions through the training data,withfor the occurrence of emotionk,andfor the absence of emotionk.

IV.BAYESIAN INFERENCE

Bayesian inference estimates the value of a random variable based on the Bayes’theorem,by deriving its posterior probability from the product of its prior and an observation likelihood.For the proposed Bayesian models in this paper,we employ a Gibbs sampling algorithm as the Bayesian inference method,to estimate the values in topiczdi,word emotionedik,and document emotionEdk,by deriving their posterior probabilities respectively.

Gibbs sampling is an efficient Bayesian inference algorithm,in which samples of the random variables are iteratively drawn from their estimated posterior probabilities in a loop,by freezing the sampled values in other random variables as the observation for their likelihood calculations.The algorithm converges after a few sampling steps,and the posterior probability of each random variable can be estimated by counting the sampling history of this variable.

The Gibbs sampling algorithms for estimating topics and emotions for the DWET model and the HDWET model are described in Algorithm 1 and Algorithm 2.Both algorithms iteratively draw samples ofzdi,edik,andEdkfrom their posterior probabilities,with the parameter variables includingη,θz,θe,θEin DWET andφin HDWET collapsed out for sampling efficiency.The sampling steps repeat throughMloops until convergence,which renders a linear time complexity O(n)for both algorithms.In the following,we illustrate the derivation of posterior probabilities respectively of the topic variablezdi,the word emotion variableedik,and the document emotion variableEdkfor the DWET model and the HDWET model.

Algorithm 1 Gibbs Sampling for DWET Inference

Algorithm 2 Gibbs Sampling for HDWET Inference

A.Gibbs Sampling for DWET

We show the derived algebraic expressions of the posterior probabilities in Algorithm 1,with the detailed derivation steps illustrated in Appendix A.

For wordiof documentdwithin a corpus1For the Gibbs sampling algorithm,this corresponds to a test corpus.,the posterior probability of observing a semantic dimension(topic)j,conditioned on the observation of words,emotions,and all other topics through the corpus are given by

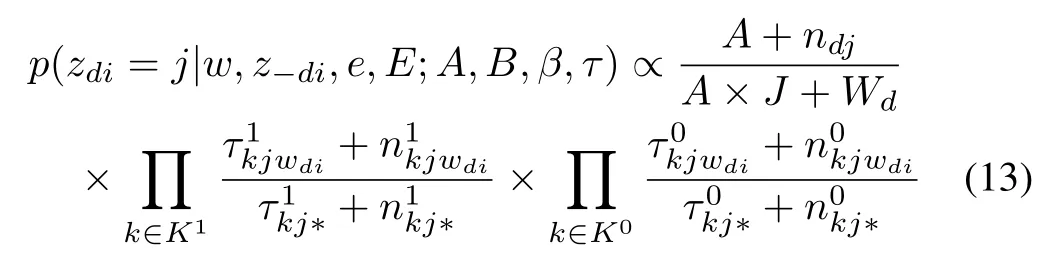
whereandrepresent the sets of occurrent and absent of emotion category in word∑counts the occurrence of topic with the same value asjin documentd,Wdcounts the number of words in documentd,counts the occurrence of word emotionk,topicj,and word with the same value aswdithrough the corpus,andcounts the absence of word emotionk,the occurrence of topicjand word with the same value aswdithrough the corpus.“∗”in the subscripts indicates a summation of the variable over the corresponding dimension.

For wordiof documentdwithin a corpus,the posterior probability of observing the emotion categorykconditioned on the observation of words,topics,and all other emotions through the corpus is given by

For documentdin a corpus,the posterior probability of observing emotion categorykconditioned on the observation of words,topics,and all other emotions through the corpus is given by

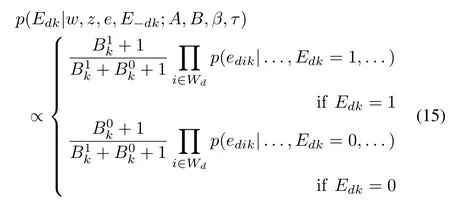
whereWdis the set of word indexes in documentd,with the posterior probabilities of word emotion observations inp(edik|...,Edk,...)calculated through(14).

In Algorithm 1,the Gibbs sampler repeatedly draws samples of topiczdi,word emotionedik,and document emotionEdkbased on the derived posterior probabilities through(13)−(15),and uses these sampled values to estimate the true posterior probabilities,until these estimated posterior probabilities get converged.We predict the values inzdi,edik,andEdkby maximizing their estimated posterior probabilities.

B.Gibbs Sampling for HDWET

We illustrate the algebraic expressions for posterior probability calculations in Algorithm 2,with the detailed derivation steps shown in Appendix B.

The HDWET model shares the similar structure and probabilistic assumptions with respect to the topic-related distributions and the word emotion-related distributions,as depicted in section III.In fact,the algebraic expressions for posterior probabilities of topics and word emotions are also the same as those in(13)and(14)respectively.

For documentdin a corpus,the posterior probability of observing emotion categorykconditioned on the observation of words,topics,and all other emotions through the corpus is given by

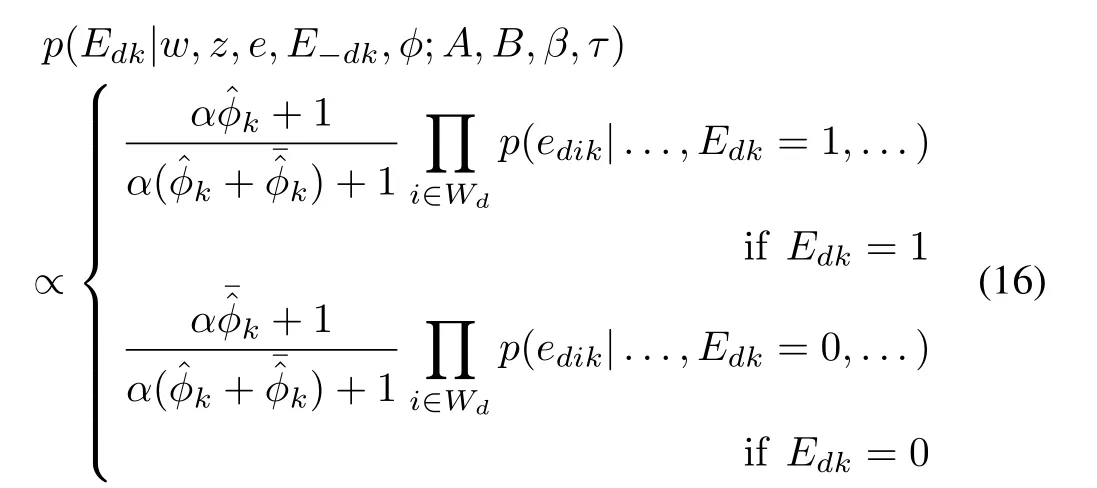
whereWdis the set of word indexes in documentd,with the posterior probability of word emotion observations incalculated through(14).is the complement ofwith,andis sampled through its updated posterior probabilitycounts the occurrence of document emotionkthrough the corpus.

Similar to the DWET model,the Gibbs sampler in Algorithm 2 repeatedly draws samples of topiczdi,word emotionedik,and document emotionEdkbased on the derived posterior probabilities through(13),(14),and(16),and estimate their true posterior probabilities based on the sampled values until convergence.Prediction of the values inzdi,edik,andEdkis made by maximizing their posterior probabilities.

V.EMOTION RECOGNITION EXPERIMENT

We examine our Bayesian inference method for textural emotion recognition in blog articles,based on the emotion corpus Ren-CECps[25].The emotion corpus contains 1,147 Chinese blog articles collected from Internet,with manually annotated emotion labels for 8 basic emotion categories in the document-level,sentence-level,and word-level,respectively.The basic emotion categories include joy,love,expect,surprise,anxiety,sorrow,anger,and hate.And each emotion label has been further distinguished into 10 levels of emotion intensities according to its emotion strength.The following is an example of emotion-annotated sentence translated from Ren-CECps:

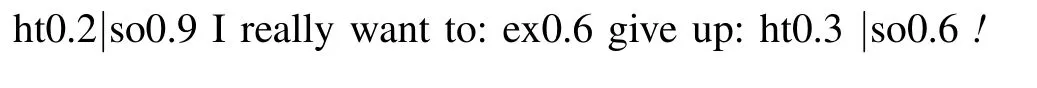
In this example,“want to”indicates a medium(0.6)expect,“give up”implies a low(0.3)hate and a medium(0.6)sorrow,while the complete sentence indicates a low(0.2)hate and a high(0.9)sorrow.

It has to be noted that emotion labels from different categories are not evenly distributed throughout the corpus[33].In fact,a previous study of the emotion classification for online messages[4]suggests that textual expression of emotions are highly biased,in which love,sorrow,and anxiety are more often observed than surprise and anger.In Ren-CECps,the number of love(over 500)is 1 magnitude larger than the number of surprise(only 90)in the document-level.This makes the textural emotion recognition very difficult for the traditional classifiers,because training a classifier on highly biased data will significantly impact the recall sores for the less common emotion categories.

The emotion corpus is divided into a training set of 917 blog articles and a test set of 230 blog articles.We initialize the concentration parametersA,B,β,τbased on the observation of corresponding categorical variables in the training set,select the model parameterJbased on a 5-fold cross validation on the training set,and set the hyper-parameterαto the number of blog articles in each set.We employ precision,recall,and fscore for evaluating the emotion recognition results in emotion category,as defined below

wherekindicates the emotion category,tpk,fpk,andfnkcount the number of true positive,false positive,and false negative predictions in the result for emotion categoryk.We compare the results from the DWET and HDWET models,perform further comparisons with those from the state-of-theart emotion prediction algorithms,and demonstrate the learned connection between emotion categories and latent semantic dimensions for specific words in the blog articles.

The detailed results of emotion prediction from the DWET and HDWET models are shown in Tables II and III for the document-level and word-level emotion recognition,respectively.Jo,Lv,Ex,Su,Ax,So,Ag,and Ht are the abbreviations for the emotions of joy,love,expect,surprise,anxiety,sorrow,anger,and hate,while Ne indicates a none emotion which only occurs in the word emotion prediction.

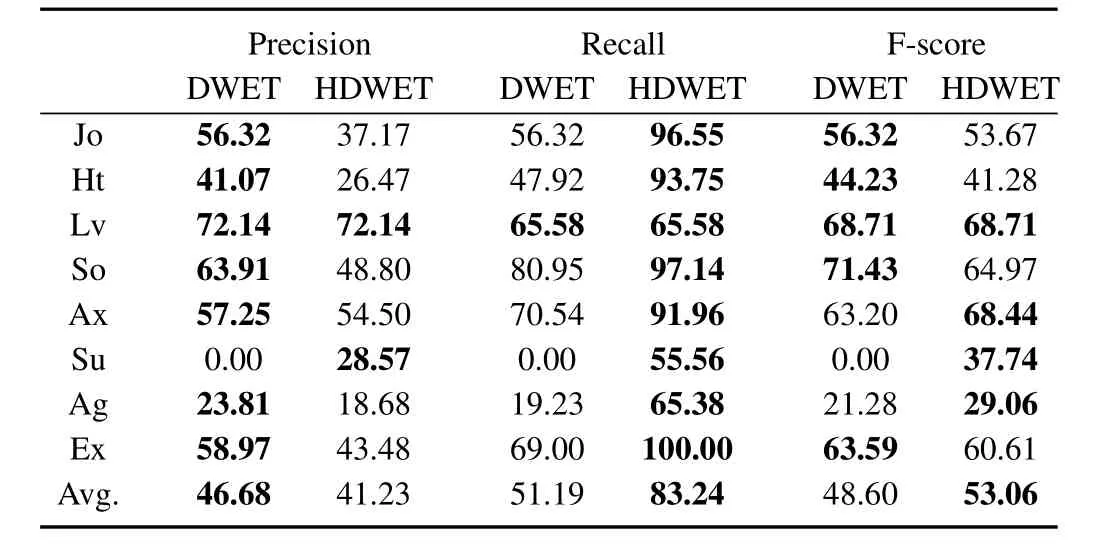
TABLE II EVALUATION OF THE DOCUMENT EMOTION PREDICTION

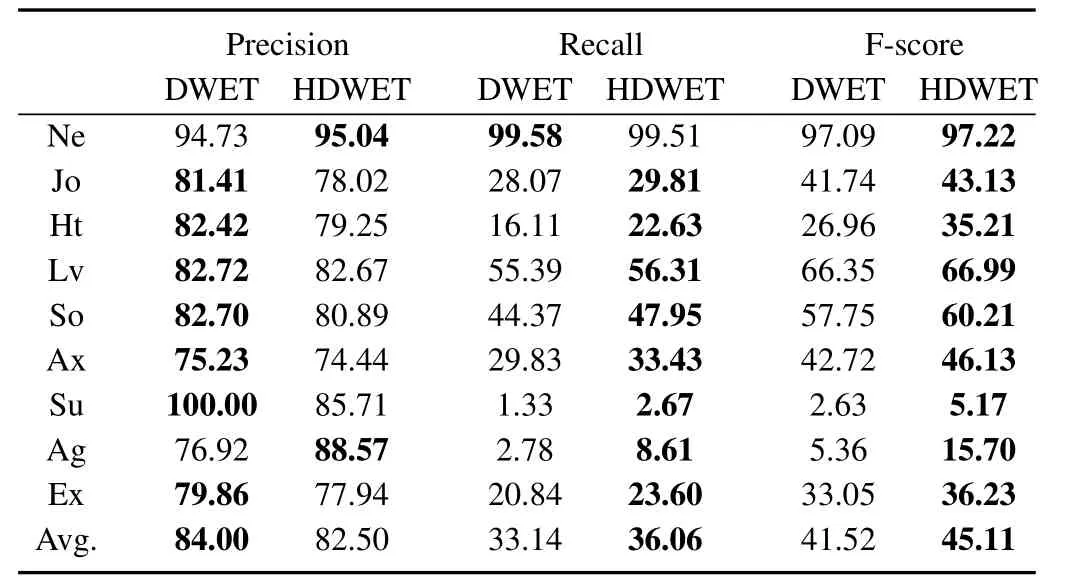
TABLE III EVALUATION OF THE WORD EMOTION PREDICTION

For document-level emotion recognition,we find that on average the DWET model achieves better precision than the HDWET model,while the HDWET model renders better Recalls than the DWET model.This can be explained by the fact that the variability in probability mass concentration parameterαφmakes the HDWET model easier to generate more positive labels for the less common emotion categories during inference.For example,Surprise is a rare document emotion compared to the other emotions,which is only observed 90 times in 1,147 blog articles in Ren-CECps.During inference,the concentration parameter variableαφSurprisegrows larger than the static concentration parameterBSurprise,which makes the posterior probability ofEdSurprise=1 in(16)larger than that in(15),and therefore enables the HDWET model to recognize more surprise labels(with a higher recall score)than the DWET model.For the common emotion categories such as love,which is observed over 500 times in 1,147 blog articles,the HDWET model still performs as well as the DWET model for generating the positive labels.This result indicates that the incorporated flexibility in document emotion concentration in the HDWET model has effectively improved the robustness for document emotion recognition.It has to be noticed that although the HDWET model achieves an average lower precision score than the DWET model,in some specific emotion categories such as love and surprise the HDWET model still renders the same or even better precision scores than the DWET model.Considering the f-score as a balanced evaluation,the HDWET model out performs the DWET model in the document-level emotion recognition.

For word-level emotion recognition,we find that both models achieve promising results for recognizing the Ne label,which in fact is the most common label for word emotion.On average,the DWET model achieves higher precision scores,while the HDWET model renders higher recall scores.The result suggests that with Bayesian inference,the flexibility in document emotion concentration not only has increased the belief in observing the less common emotion categories in documents but also has flowed through the directed connectionunder the probabilistic assumption in(3)to impact the belief for observing the same word emotions in the HDWET model.For the common emotion category such as love and sorrow,the recall scores from HDWET are still better than those from DWET,indicating that a flexible concentration parameter in the document emotion distribution could effectively improve the robustness for word emotion recognition.By considering the f-score as a balanced evaluation,we find the HDWET model also outperforms the DWET model for word-level emotion recognition.

We plot the time complexity of Gibbs sampling algorithms in Fig.3,in terms of the number of input documents,for two hundred sampling iterations of the DWET and HDWET inference respectively.Our results suggest that inference time of both algorithms grows linearly with respect to the size of evaluation data,and that the DWET and HDWET models render very little difference in the time complexity.

Fig.3.Time complexity of Gibbs sampling algorithms for Algorithm 1 and Algorithm 2 in terms of document number.

We plot the receiver operating characteristic(ROC)curves in Fig.4 for the results of document emotion prediction and word emotion prediction,in terms of DWET and HDWET respectively.A comparison of Figs.4(a)and(b)suggests that the HDWET model could significantly improve the robustness of document emotion classification,especially for the rare emotion categories,e.g.,surprise and anger,in contrast to the DWET model.By comparing Figs.4(b)and(d),we find that the DWET model outperforms the HDWET model in the robustness of emotion classification for sorrow and surprise,while the HDWET model could generate robust classification results for more difficult emotion categories like hate and expect with properly selected thresholds.

Next,we compare our Bayesian models with the state-of-the-art emotion prediction algorithms for the document-level and word-level emotion recognition respectively,as shown in Figs.5 and 6,based on the Precision scores.The naive Bayesian(NB)and SVM classifiers are employed as the base-line models for the document emotion recognition,and the hidden Markov models(HMM)and conditional random fields(CRF)are employed as the base-line models for the word emotion recognition.For the document-level emotion recognition in Fig.5,we find that the NB classifier performs slightly better than the SVM classifier,with the average precisions of 30.54%and 28.41%,respectively.Our DWET and HDWET models perform much better than the base-line models,with the average precisions of 46.68%and 41.23%,respectively.For word-level emotion recognition in Fig.6,the experiment results suggest that the CRF model performs slightly better than the HMM model,with the averaged precisions of 63.46%and 62.20%,respectively.Compared with the base-line models,our DWET and HDWET models render much better results for word emotion recognition,with the average precisions of 84.00%and 82.50%,respectively.These comparisons suggest that,our Bayesian models by incorporating the latent semantic dimensions as the context of words have generated a much simpler representation of emotions in the natural language expression,which helps the models to fit more easily than the dictionary feature based models.

Fig.4.ROC curves for document emotion prediction(a,c)and word emotion prediction(b,d)in terms of the DWET model(a,b)and the HDWET model(c,d).

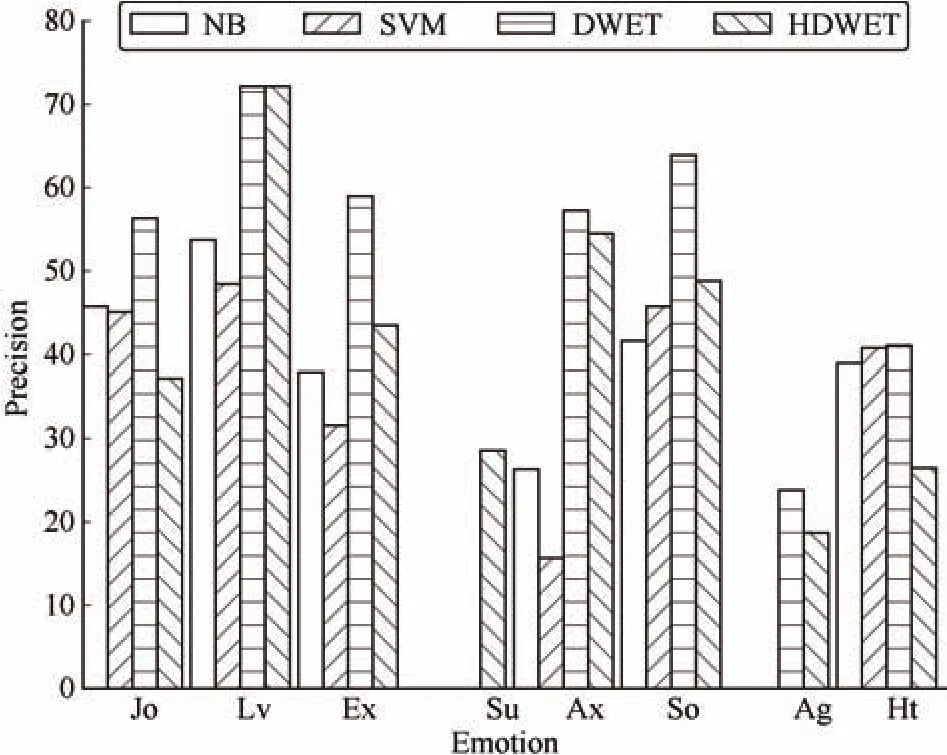
Fig.5.Document emotion precisions from NB,SVM,DWET,and HDWET.

Fig.6.Word emotion precisions from HMM,CRF,DWET,and HDWET.

Fig.7 demonstrates the know ledge of emotion in natural language expression with respect to the semantic dimensions(topics),in the form of an emotion-topic diagram.The know ledge is learned with the HDWET model.We connect words to their most significant semantic dimensions(T1,...,T9),and attach these semantic dimensions to their related emotions,and denote the connection strengths denoted on the edges.The node colors specify the category of a node.For example,all word nodes related to the same topic together with this topic node share the same color.An emotion node shares the same color with its most strongly connected topic node.With this emotion-topic diagram,we can easily tell the connection between words,semantic dimensions,and emotions.For example,words like“convalesce”and “fall behind”in their most significant semantic dimension T3 are strongly connected to the emotion of sorrow.Words in the emotion-topic diagram are not necessarily the emotional words in traditional definition,because we are generalizing the know ledge of emotion expression from manual annotations to the more general language expressions.

The know ledge of emotion expression with respect to the semantic dimensions has been learned through the V-structure ofin both models.The“explaining away”phenomenon allows topiczto directly influence the posterior probabilities of emotion labelsethrough(14),and enables the reverse influence from word emotion sampleseto the posterior probabilities of topicszthrough(13).The models could therefore recognize the emotion labelsein the same word with different semantic dimensionsz,which promises an improved precision,and associate each semantic dimensionzwith a specific distribution of emotionse,which generalize the basic know ledge of emotion with respect to many general natural language expressions to improve the recall.

Fig.7.Part of the emotion-topic diagram generated from HDWET.

V I.CONCLUSION

In this paper,we propose two Bayesian models DWET and HDWET for exploring the latent semantic dimensions as the context in natural language,and for learning the know ledge of emotion expressions with respect to these semantic dimensions.The basic idea is that probabilistic influence could flow between emotions and topics in Bayesian inference through a V-structure in the models,in which the emotion variableeand the topic variablezare located as two parents of the observed word variablew.Because each discrete value in topiczrepresents a specific context semantic dimension for the associate wordw,the probabilistic distribution over topics in Bayesian inference corresponds to a vector representation of the probabilities over different context semantic dimensions,which allows the models to distinguish words under different contexts and effectively improves the emotion recognition results.Our experiment of the document-level and word level emotion predictions,based on the Chinese emotion corpus Ren-CECps,demonstrates a promising improvement for emotion recognition compared to the state-of-the-art emotion recognition algorithms.The DWET model outperforms all base-line algorithms for word and document emotion predictions.And the HDWET model,with a flexible concentration parameterφinjected in the hierarchy of corpus-level document emotion distribution,allows a self-adjustment of emotion distributions through different documents,and significantly improves emotion recognition for the less common emotion categories with even better Recalls and F-scores compared to the DWET model.We demonstrate the know ledge of emotion expression with respect to latent semantic dimensions through an emotion-topic diagram.By explicitly connecting semantic indexes with emotion categories and the closely related words,the diagram makes it easier to understand the semantic meanings in most general words and their underlying connections to the human emotions.

Our Bayesian models have simplified the language features for textual emotion recognition,by representing the word context with latent semantic dimensions and by associating emotion categories with the word contexts in a low dimensional feature space.However,our features could be somehow over-simplified because the context information in natural language expressions is still richer than the discrete semantic dimensions which we can maximally afford in our models.If we set too many semantic dimensions in the model,the probabilistic influence would flow wildly and the Bayesian inference could never converge.Another promising direction for exploring the rich context semantic information is through a deep neural network with multi-layer abstractions.The neurons are very different from our topic variables in that they do not separately(or linearly)represent semantic dimensions,but can be combined together to specify one point in a large semantic space,whose dimension is exponential to the number of neurons.In this sense,we would like to employ the deep neural networks for learning emotion expressions in natural language with a better semantic representation in our future work.

APPENDIX A DERIVING POSTERIOR PROBABILITIES FOR DWET

The Bayes’theorem suggests that for a random variablexits posterior probability is proportional to the product of its prior probability and likelihood of other related observations iny.For a complicated Bayesian model,often there are many other variables which are not directly involved in the Bayesian inference,for which we useoto represent.We employ the following equation to represent the Bayes’theorem with the non-directly involved variables on the condition part

We illustrate the posterior probability derivations based on this equation.

In Section III,we make assumptions of conjugate prior probabilities for the proportional parameters,to simplify our Bayesian inference.This is because that with these conjugate prior probabilities,we can have a closed-form expression of their posterior probabilities after observing values in the related variables.For example,the proportional parameterin(9)is assumed a Beta prior probability,which is the conjugate prior of its Bernoulli likelihood function in(4).After observingEthrough the documents in the test set,we can have posterior probability ofin a closed-form

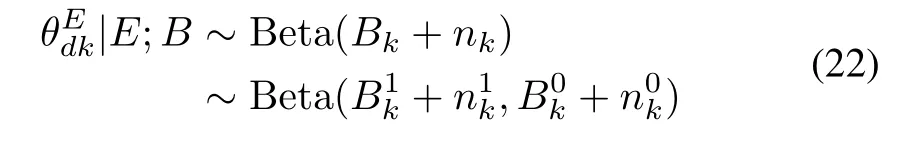
in whichcounts the occurrence and absence of document emotionkin this set.

The topic variablezdi,which specifies a semantic dimension for wordwdi,has its posterior probability factorized by following the Bayes’theorem

in which“−”on the subscript indicates the set of all variables except the one specified with the subscript.zdiin(23)corresponds to the variable of interestxin(21),wdicorresponds to the related observationy,and the rest variables ofw−di,z−di,e,andEcorrespond too.A,B,β,andτare parameters in these probabilistic distributions.

We follow the categorical distribution assumption for the topic variablezdiin(2),and interpret the value of the first factor in(23)

The proportional parameter variablecan be inferred through its posterior probability after observingzdin documentd

in whichWd=nd∗is the number of words in documentd.

Similarly,by following the assumption of Categorical distribution for the word variablewdiin(23),we can derive the algebraic expression for the second factor in(23)

in which “∗”indicates a summation over the corresponding dimension.

We take(26)and(29)into(23)to derive the algebraic expression of the posterior probability of topic variablezdiin(13).

Next,we factorize the posterior probability of word emotion variableedikby following the Bayes’theorem

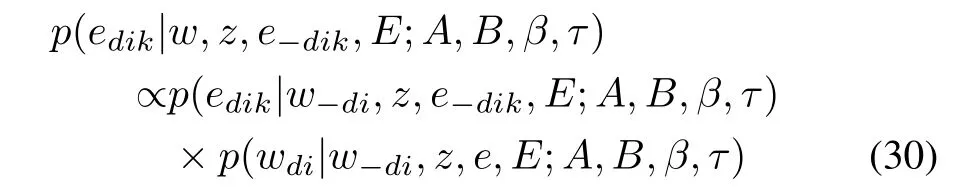
in whichedikcorresponds to the variable of interestxin(21),wdicorresponds to the related observationy,and the rest variablesw−di(all words exceptwdi),z,e−dik,andEcorresponds too.A,B,β,andτare parameters in these probabilistic distributions.

We follow the Bernoulli distribution assumption for the word emotion variableedikin(3),and interpret the probability value of the first factor in(30)

in whichcan be inferred through its posterior probability after observing the document emotion and other word emotions in documentd

This is because the prior probability Beta forθein(8)is the conjugate prior of its Bernoulli likelihood function in(3).And becauseθeis a document-level variable as shown in Fig.1,we can simply update its parameters with observations in the specific documentdto get its posterior probability.In(32),ed·kcorresponds to all the word emotion labels in documentdand emotion categorycounts the occurrence of word emotionkin documentd.A replacement ofθein(31)with its expectation in(32)gives the algebraic expression for the first factor of word emotion posterior probability in(30)

in whichWdis the number of words in documentd,andWd−ndkcorresponds to the absent count of word emotionkin documentd.

The second factor in(30)is exactly the same as that in(23),whose derivation can be found in(27).We extend its expression by extracting the emotion categorykout of the product for the convenience of later derivation,which gives

in whichK1/kandK0/krepresent the sets of occurred and absent emotion categoriesk′in wordwdiexceptk,respectively.Because the products overK1andK0exceptkturn to be the same regardless of the assignment inedikin(34),we could take them out to simplify the calculation.

We take(33)and(34)into(30)to derive the algebraic expression of the posterior probability of word emotion variableedikin(14).

Finally,we factorize the posterior probability of document emotion variableEdkby following the Bayes’theorem

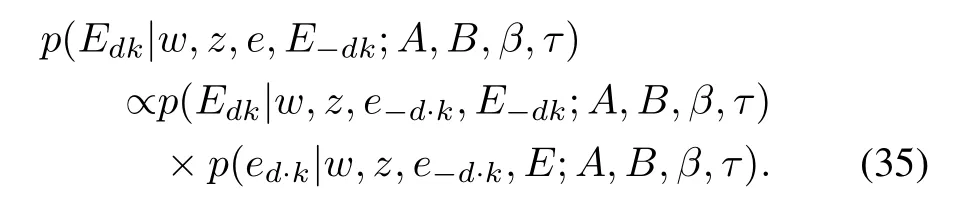
We follow the Bernoulli distribution assumption for the document emotion variableEdkin(4),and interpret the probability value of the first factor in(35)

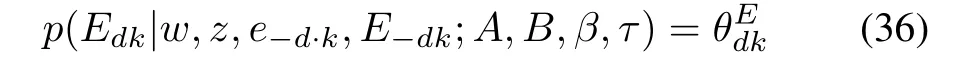
in whichcan be inferred through its posterior probability after observing the document emotions as described in(22).A replacement ofin(36)with its expectation in(22)gives the algebraic expression for the first factor of document emotion posterior probability in(35)

As illustrated in the derivation of(27),we assume that different emotion categories are independent,and gives the factorized production of the second factor in(35)

We take(37)and(38)into(35)to derive the algebraic expression of the posterior probability of document emotion variableEdkin(15).

APPENDIX B DERIVING POSTERIOR PROBABILITIES FOR HDWET

The posterior probabilities for topic variablezdiand word emotion variableedikin the HDWET model are the same as those in the DWET model.For the document emotion variableEdk,we factorize its posterior probability by following the Bayes’theorem to get

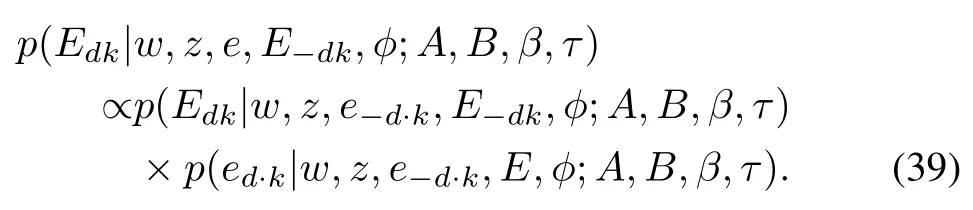
For the first factor in(39),we derive the same algebraic expression for the prior probability of document emotionEdkas(36),but derive the expectation ofdifferently as follows.Because the proportional parameterfor document emotion distribution in the HDWET model follows the Beta distribution with a flexible concentration parameterαφkin(11),we infer its poster probability from the samplesof the concentration parameterφk.

In the model construction for HDWET,the flexible concentration variableφkis assumed to follow the Beta distribution in(12).Because its related observation in document emotion variableEdkfollows the Bernoulli distribution in(4),the posterior probability ofφkcan be derived with a closed form expression with corresponding distribution parametersBkupdated as in(17).We take the sampled values offor variableφkto have the algebraic expression for the first factor in(39)

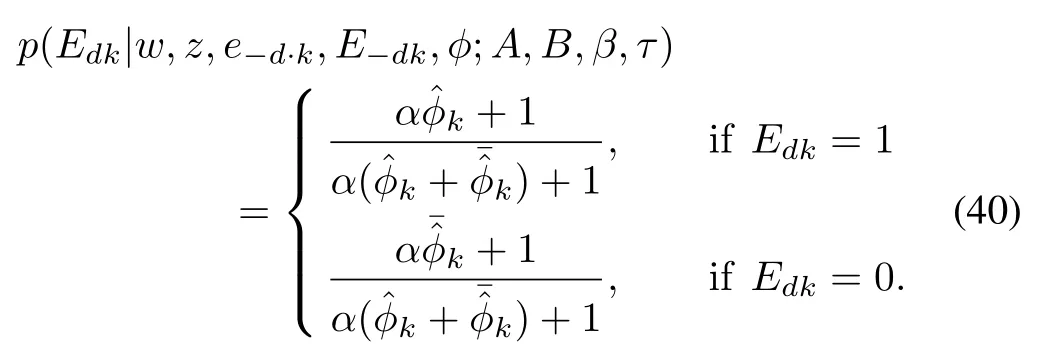
For the second factor in(39),because word emotion variablesed·kshares the same model structure and probabilistic assumptions in HDWET and DWET,the derivation of its posterior probability turns to be the same as that of the DWET model,which gives

We take(40)and(41)into(39)to derive the algebraic expression of the posterior probability of the document emotion variableEdkfor the HDWET model in(16).

[1]H.Gunes and B.Schuller,“Categorical and dimensional affect analysis in continuous input:Current trends and future directions,”Image Vision Comput.,vol.31,no.2,pp.120−136,Feb.2013.

[2]J.-C.Lin,C.-H.Wu,and W.-L.Wei,“Error weighted sem i-coupled hidden Markov model for audio-visual emotion recognition,”IEEE Trans.Multimedia,vol.14,no.1,pp.142−156,Feb.2012.

[3]S.Scherer,M.Glodek,G.Layher,M.Schels,M.Schm idt,T.Brosch,S.Tschechne,F.Schwenker,H.Neumann,and G.Palm,“A generic framework for the inference of user states in human computer interaction,”J.Multimodal User Interfaces,vol.6,no.3−4,pp.117−141,Nov.2012.

[4]F.J.Ren,X.Kang,and C.Q.Quan,“Exam ining accumulated emotional traits in suicide blogs with an emotion topic model,”IEEE J.Biomed.Health Inform.,vol.20,no.5,pp.1384−1396,Sep.2016.

[5]H.Mo,J.Wang,X.Li,and Z.L.Wu,“Linguistic dynamic modeling and analysis of psychological health state using interval type-2 fuzzy sets,”IEEE/CAA J.Automat.Sin.,vol.2,no.4,pp.366−373,Oct.2015.

[6]L.Bylsma,B.H.Morris,and J.Rottenberg,“A meta-analysis of emotional reactivity in major depressive disorder,”Clin.Psychol.Rev.,vol.28,no.4,pp.676−691,Apr.2008.

[7]G.Domes,L.Schulze,and S.C.Herpertz,“Emotion recognition in borderline personality disorder-a review of the literature,”J.Pers.Disord.,vol.23,no.1,pp.6−19,Feb.2009.

[8]K.A.Lindquist,T.D.Wager,H.Kober,E.Bliss-Moreau,and L.F.Barrett, “The brain basis of emotion:a meta-analytic review,”Behav.Brain Sci.,vol.35,no.3,pp.121−143,Jun.2012.

[9]J.T.Buhle,J.A.Silvers,T.D.Wager,R.Lopez,C.Onyemekwu,H.Kober,J.Weber,and K.N.Ochsner,“Cognitive reappraisal of emotion:a meta-analysis of human neuroimaging studies,”Cereb.Cortex,vol.24,no.11,pp.2981−2990,Nov.2014.

[10]C.H.Yang,K.H.Y.Lin,and H.H.Chen,“Emotion classification using web blog corpora,”inProc.IEEE/WIC/ACM Int.Conf.Web Intelligence,Fremont,CA,2007,pp.275−278.

[11]R.Tokuhisa,K.Inui,and Y.Matsumoto,“Emotion classification using massive examples extracted from the web,”inProc.22nd Int.Conf.Computational Linguistics,Manchester,United Kingdom,2008,pp.881−888.

[12]I.Maks and P.Vossen,“A verb lexicon model for deep sentiment analysis and opinion mining applications,”Proc.2nd Workshop on Computational Approaches to Subjectivity and Sentiment Analysis,Portland,Oregon,USA,2011,pp.10−18.

[13]S.M.Mohammad and T.Yang,“Tracking sentiment in mail:How genders differ on emotional axes,”Proc.2nd Workshop on Computational Approaches to Subjectivity and Sentiment Analysis,Portland,Oregon,USA,2011,pp.70−79.

[14]A.Balahur,J.M.Hermida,and A.Montoyo,“Detecting implicit expressions of emotion in text:A comparative analysis,”Decis.Support Syst.,vol.53,no.4,pp.742−753,Nov.2012.

[15]W.Y.Liand H.Xu,“Text-based emotion classification using emotion cause extraction,”Expert Syst.Appl.,vol.41,no.4,pp.1742−1749,Mar.2014.

[16]S.Matsumoto,H.Takamura,and M.Okumura,“Sentiment classification using word sub-sequences and dependency sub-trees,”inAdvances in Know ledge Discovery and Data Mining,T.B.Ho,D.Cheung,and H.Liu,Eds.Hanoi,Vietnam:Springer,2005,pp.301−311.

[17]T.Kudo and Y.Matsumoto,“A boosting algorithm for classification of semi-structured text.inProc.2004 Conf.Empirical Methods in Natural Language Processing,Barcelona,Spain,2004,pp.301−308.

[18]C.H.Yang,K.H.Y.Lin,and H.H.Chen,“Building emotion lexicon from we blog corpora,”inProc.45th Annu.Meeting of the ACL on Interactive Poster and Demonstration Sessions,Prague,Czech Republic,2007,pp.133−136.

[19]N.Kobayashi,K.Inui,Y.Matsumoto,K.Tateishi,and T.Fukushima,“Collecting evaluative expressions for opinion extraction,”inProc.1st Int.Joint Conf.Natural Language Processing,Hainan Island,China,2004,pp.596−605.

[20]H.Teramura,“Japanese syntax and meaning,”Kurosio Publishers,1982.

[21]X.Hu,J.S.Downie,and A.F.Ehmann,“Lyric text mining in music mood classification,”inProc.10th Int.Society for Music Information Retrieval Conf.,Kobe,Japan,2009,pp.411−416.

[22]C.Strapparava and A.Valitutti,“Word Net-affect:an affective extension of word Net,”inProc.4th Int.Conf.Language Resources and Evaluation,Lisbon,Portugal,2004,pp.1083−1086.

[23]P.Singh,“The public acquisition of commonsense know ledge,”inProc.AAAI Spring Symposium:Acquiring(and Using)Linguistic(and World)Know ledge for Information Access,Palo A lto,CA,2002.

[24]H.Liu,H.Lieberman,and T.Selker,“A model of textual affect sensing using real-world know ledge,”inProc.8th Int.Conf.Intelligent User Interfaces,M iam i,Florida,USA,2003,pp.125−132.

[25]C.Q.Quan and F.J.Ren,“A blog emotion corpus for emotional expression analysis in Chinese,”Comput.Speech Lang.,vol.24,no.4,pp.726−749,Oct.2010.

[26]S.Aman and S.Szpakowicz,“Identifying expressions of emotion in text,”inText,Speech and Dialogue,V.Matoušek and P.Mautner,Eds.Pilsen,Czech Republic:Springer,2007,pp.196−205.

[27]X.Kang,F.J.Ren,and Y.N.Wu,“Semisupervised learning of authorspecific emotions inmicro-blogs,”IEEJ Trans.Electrical&Electronic Eng.,vol.11,no.6,pp.768−775,Nov.2016.

[28]Y.N.Wu,K.Kita,F.J.Ren,K.Matsumoto,and X.Kang,“Modification relations based emotional keywords annotation using conditional random fields,”inProc.4th Int.Conf.Intelligent Networks and Intelligent Systems,Kunm ing,China,2011,pp.81−84.

[29]Y.N.Wu,K.Kita,F.J.Ren,K.Matsumoto,and X.Kang,“Exploring emotional words for Chinese document chief emotion analysis,”inProc.25th Pacific Asia Conf.Language,Information and Computation,Singapore,2011,pp.597−606.

[30]D.Dasand S.Bandyopadhyay,“Word to sentence level emotion tagging for Bengali blogs,”inProc.ACL-IJCNLP 2009 Conf.Short Papers,Suntec,Singapore,2009,pp.149−152.

[31]X.Kang,F.J.Ren,and Y.N.Wu,“Bottom up:Exploring word emotions for Chinese sentence chief sentiment classification,”inProc.2010 Int.Conf.Natural Language Processing and Know ledge Engineering(NLPKE),Beijing,China,2010.

[32]X.Kang and F.J.Ren,“Sampling latent emotions and topics in a hierarchical Bayesian network,”inProc.2011 7th Int.Conf.Natural Language Processing and Know ledge Engineering(NLP-KE),Tokushima,2011,pp.37−42.

[33]F.J.Ren and X.Kang,“Employing hierarchical Bayesian networks in simple and complex emotion topic analysis,”Comput.Speech Lang.,vol.27,no.4,pp.943−968,Jun.2013.