Guaranteed Cost Consensus for High-dimensional Multi-agent Systems With Time-varying Delays

Zhong Wang,M ing He,Tang Zheng,Zhiliang Fan,and Guangbin Liu

I.INTRODUCTION

RECENTLY many researchers paid much attention to the distributed coordination control of multi-agent systems due to its broad practical applications including formation control of mobile agents[1],synchronization in wireless sensor networks[2],distributed automatic generation control for cyber-physical microgrid system[3],and rendezvous[4]or flocking[5]of multiple vehicles.Consensus is an essential problem for multi-agent systems and it has been extensively investigated(see the survey papers[6]−[8]and the references therein).

In the existing works,an important topic on the consensus problems is the effect of time delays which include computational delays of agents and transmission delays in the transfer of data between agents.Based on the frequency domain analysis,the Lyapunov function and the concept of delayed and hierarchical graph,many conclusions for low-dimensionalmulti-agent systems with time delays were obtained for single integrator cases(e.g.,[9]−[12])and double-integrator cases(e.g.,[13]−[16]).For high-dimensional cases,the dynamics of each agent can be described as high-order integrator[17]−[19].In fact,agents of high-dimensional cases were depicted by the state space approach in most of works[20]−[23],where the analysis approach included the frequency domain analysis,the Lyapunov function approach and the property of nonnegative matrix.

With the development of the control theory,it is usually desirable to design a controller which not only stabilizes the system but also ensures an adequate level of performance.To this end,a design approach is so-called guaranteed cost control[24]−[26],where the performance and the energy consumption are considered simultaneously.In the aforementioned works on consensus problems,only the consensus regulation performance for multi-agent systems was considered.However,the energy consumption is also essential for the consensus.Thus,the idea of guaranteed cost control should be applied for the consensus problem to simultaneously consider the consensus regulation performance and the control energy consumption.To the best of our know ledge,there are very few works to investigate guaranteed cost consensus problems.In[27]−[30],the guaranteed cost consensus problems for lowdimensional multi-agent systems were investigated.For highdimensional multi-agent systems,[31]studied the guaranteed cost leader-follower control.In[32],the problem of event based guaranteed cost consensus for high-dimensional multiagent systems was considered based on a sampled-data event triggering mechanism.It should be pointed out that the effects of time delays for guaranteed cost consensus problems were not considered in[28]−[32].

Motivated by this,guaranteed cost consensus problems for high-dimensional multi-agent systems with time-varying delays are investigated in the current paper.Comparing with the existing works,there are two contributions.On one hand,the guaranteed cost consensus problems are introduced into high dimensional multi-agent systems.In[27]−[30],each agent of multi-agent systems was described as low-dimensional integrator dynamics.But those analysis approaches cannot be directly used to the guaranteed cost consensus problem for high-dimensional case.On the other hand,the effects of time-varying delays are considered,while the works in[28]−[32]did not consider this issue.In[27],the guaranteed cost consensus problem for first-order multi-agent systems with time delays were studied,but the time delay is time-invariant.

The remainder of this paper is organized as follows.In Section II,the graph theory is given and the problem descrip-tion of guaranteed cost consensus is presented.In Section III,sufficient conditions for guaranteed cost consensus are given,an upper bound of the cost function is determined,and an approach is proposed to obtain the consensus function.In Section IV,a numerical simulation is given.Finally,concluding remarksare stated in Section V.Throughout the current paper,{A1,A2,...,An}represents a block-diagonal matrix withAi(i=1,2,...,n)on its diagonal,1N∈RNdenotes anN-dimensional column vector with all components 1,0 is used to denote zero matrices of any size with zero vectors and zero number as special cases.IN∈RN×Nrepresents the identity matrix of sizeN.The symbol⊗is used to represent the Kronecker product.The notation asterisk∗represents the elements below the main diagonal of a symmetric matrix.

II.PRELIMINARIES

An undirected graphG=G(V,E,W)consists of anode setV={v1,v2,...,vN},an edge setand a symmetric adjacency matrixW=[wij]∈RN×Nwithwij≥0 andwii=0,wherewij＞0 if and only if(vj,vi)∈E.The node index belongs to a finite index setIN={1,2,...,N}.The neighboring set of nodeviis denoted byN i={vj∈V:(vj,vi)∈E}.The degree of nodeviis defined as∑ and the degree matrix ofGasD=The matrixL=D−Wis called the Laplacian matrix associated withG.If there does not exist an isolated node inG,thenGis said to be connected.

The following lemma shows basic properties of the Laplacian matrix of an undirected graph.

Lemma 1[33]:LetL∈RN×Nbe the Laplacian matrix of an undirected graphG,then 1)Lat least has a zero eigenvalue,and 1Nis an associated eigenvector;that is,L1N= 0.2)IfGis connected,then 0 is a simple eigenvalue ofL,and all the otherN−1 eigenvalues are positive;that is,0=λ1＜λ2≤···≤λN,whereλi(i∈IN)denotes the eigenvalue ofL.

A high-dimensional multi-agent system composed ofNhomogeneous agents is considered.The interaction topology can be described by an undirected graphG,each node stands for an agent,the edge between any two nodes denotes the interaction channel between them,and the weight of the edge corresponds to the interaction strength.Each agent can be described as general linear dynamics:

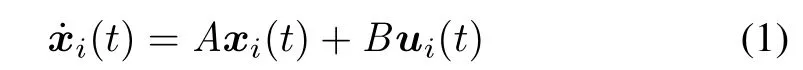
wherei=1,2,...,N,A∈Rd×dandB∈Rd×mare constant matrices,xi(t)is the state of agenti,ui(t)is the control input of agenti.The statex(t)ismarked asx(t)=.Then,the multi-agent system can be rewritten as

Consider the following consensus protocol

wherei,j∈{1,2,...,N},K∈Rm×dis a control gain matrix,N irepresents the neighboring set of agenti,wijis the interaction strength of the edge from agentjto agentiandτ(t)denotes the time-varying delay during the information communication.The time-varying delayτ(t)satisfies0≤τ(t)andwhereτmaxandℓare known positive constants.In global form,the consensus protocol is

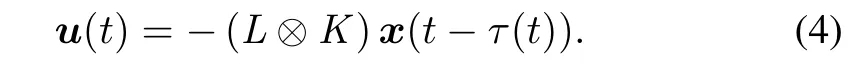
Then,the dynamics of multi-agent system(2)with protocol(4)can be described by

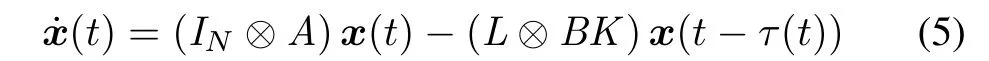
where

Letrepresents the state error between agentjand agenti,define the following cost function for multi-agent system(5)with symmetric and positive definite matrices

where

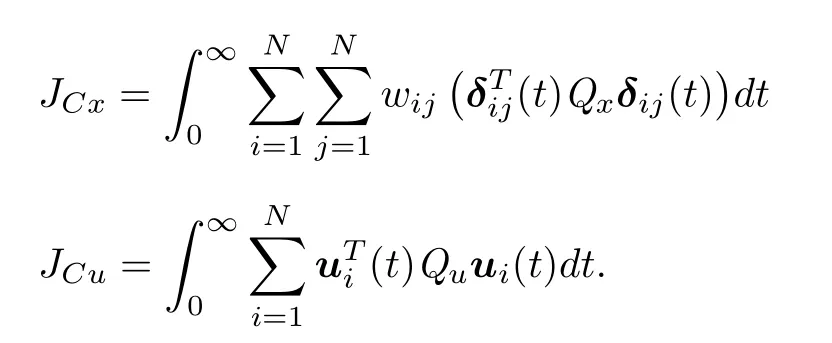
Definition 1:Multi-agent system(5)is said to achieve guaranteed cost consensus if there exists a vector-valued functionsuch thatand there exists a positive scalarsuch thatwherec(t)is called a consensus function andis said to be a guaranteed cost.

Definition 2:Multi-agent stem(2)is said to be guaranteed cost consensualizable by control protocol(4)if there exists a control gain matrixKsuch that the multi-agent system achieves guaranteed cost consensus.

Remark 1:In cost function(6),JCxandJCucan be regarded as the consensus regulation performance and control energy consumption for high-dimensional multi-agent systems,respectively.Because consensus problems for multiagent systems focus on state errors among neighboring agents instead of states of all agents,JCxis constructed by state errors.The guaranteed cost consensus problem is to find a control gain matrixKsuch that the cost functionJChas a guaranteed cost upper bound

III.MA IN RESULTS

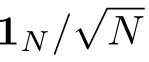
which satisfies thatUT U=INand

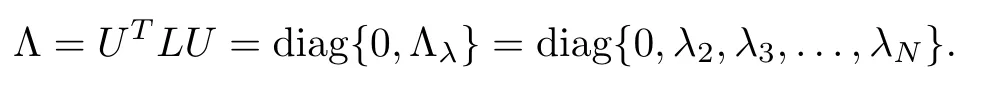
Let

whereκc(t)∈Rdandthen multi-agent system(5)can be transformed into

where

For cost function(6),it can be shown that

Thus,by(7)and(10),it can be seen that

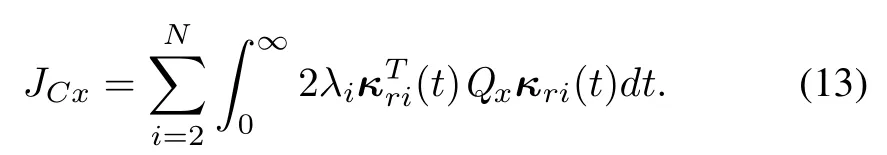
Similarly,by(7)and(11),one has

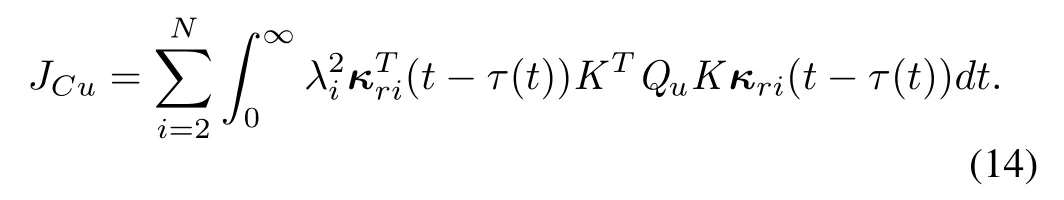
Thus,one can obtain that cost function(6)can be rewritten as

Before obtaining the main result,the following lemma should be introduced.

Lemma 2[34]:Letκ(t)∈Rdbe a vector-valued function with first-order continuous-derivative entries.Then the following integral inequality holds for any matrices Φ1,Φ2∈Rd×d,d-dimensional matrixW=W T＞0,and a scalar functionτ(t)≥0:

where

The following theorem presents a sufficient condition for guaranteed cost consensus.

Theorem 1:Multi-agent system(5)with an undirected and connected topologyGachieves guaranteed cost consensus if there existd-dimensional matricesP=PT＞0,R=RT＞0,W=W T＞0,Φ1and Φ2such that

where

Proof:Firstly,let

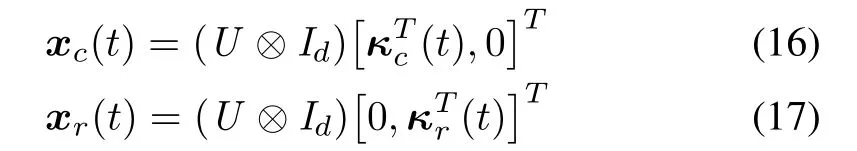
where 0∈R1×(N−1)din(16)and 0∈R1×din(17).Due toUis an orthogonal matrix,thenxc(t)andxr(t)are linearly independent.By(7),one has

By(16),it can be obtained that

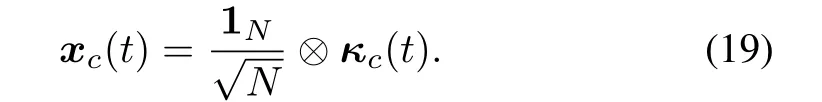
Thus,it follows that multi-agent system(5)achieves consensus if and only if subsystem(9)is asymptotically stable;that is,

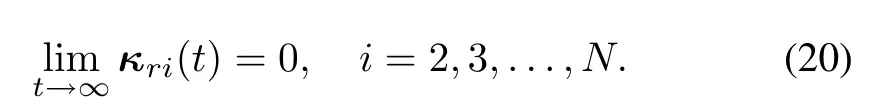
Next,consider the following Lyapunov-Krasovskii function(LKF)candidate

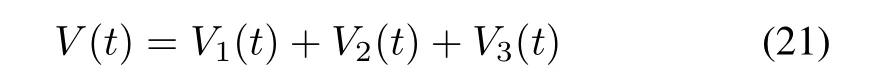
where

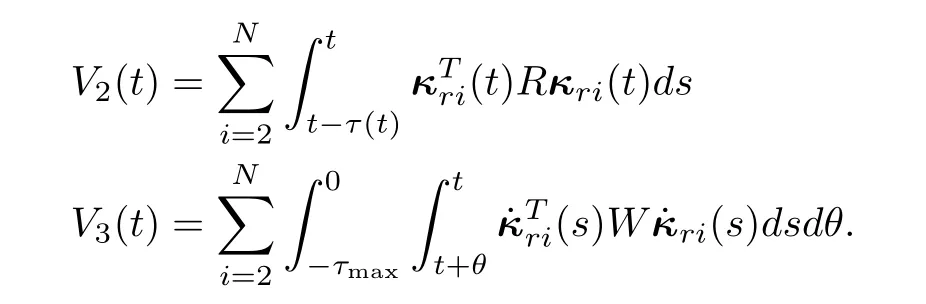
Then,the time derivative ofV(t)along the trajectory of(9)is

From(9),one has

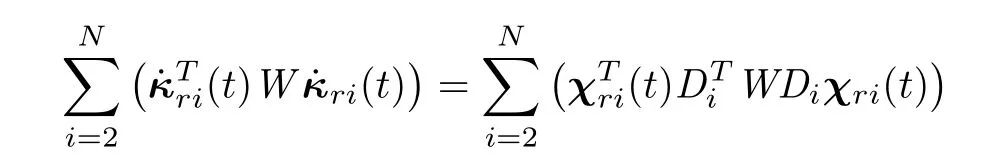
whereand the matrixD i=By Lemma 2,it can be obtained that

Then,

Moreover,define

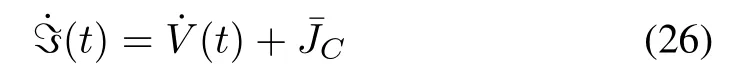
where

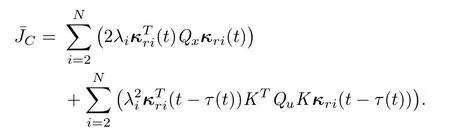
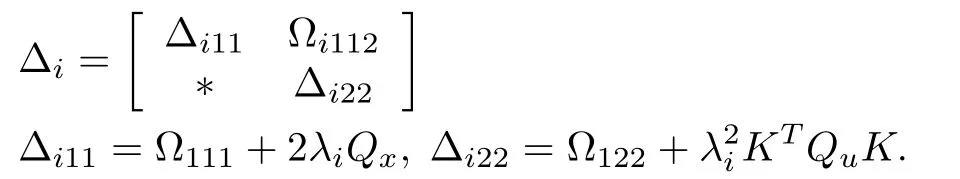
Hence,by the Schur complement,if Ωi＜0(i=2,3,...,N),then Θi＜0(i=2,3,...,N).Thus,andif and only ifThen,andif and only if...,N).Moreover,by the convex property of linear matrix inequalities(LM Is),ifΩi＜0(i=2,N)then Ωi＜0(i=2,3,...,N).Therefore,if Ωi＜0(i=2,N),subsystems(9)are asymptotically stable.

Sinceandthen limt→∞V(t)=0.Integrating both sides of(28),one haswhere the fact thathas been used.Therefore,from Definition 1,can ensure that multi-agent system(5)achieves guaranteed cost consensus and the cost function satisfiesJC≤V(0).The conclusion of Theorem 1 can be obtained.

Remark 2:By using the state space decomposition approach,guaranteed cost consensus problems for the high-dimensional multi-agent systems with time delays are converted into guaranteed cost stability problems forN−1 time-delayed subsystems.It is worth pointing out that Theorem 1 only needs to judge whether two matrices are negative;that is,the LMI criteria are only dependent on the second smallest eigenvalueλ2and the maximum eigenvalueλNofL.However,λ2andλNofLmay be difficult to be obtained when the dimensionNofLis huge.Fortunately,[33]gives a method to estimateλ2and the Gersgorin Disc Theorem in[35]can be used to approximately determineλN.

When multi-agent system(5)achieves guaranteed cost consensus,an upper bound of guaranteed cost function(6)and the explicit expression of the consensus function are obtained by the following theorem and corollary,respectively.

Theorem 2:When multi-agent system(5)achieves guaranteed cost consensus withKandd-dimensions matricesP=PT＞0,R=RT＞0,the guaranteed cost satisfies

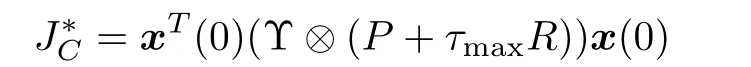
Proof:From(7),it can be obtained thatThen,one can obtain that

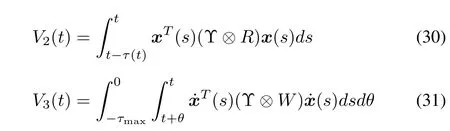
where

Thus,the conclusion of Theorem 2 can be obtained.

Corollary 1:When multi-agent system(5)achieves guaranteed cost consensus,the consensus functionc(t)satisfies

Proof:From(8),one can obtain thatBy(7),one has

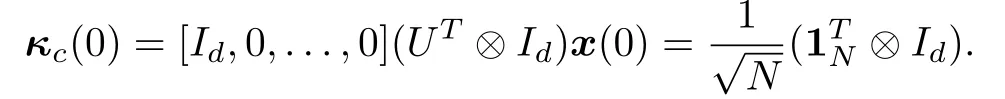
Thus,it can be obtained that

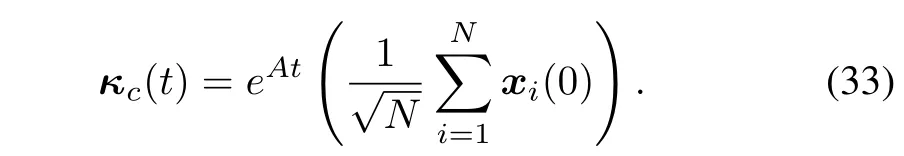
From the proof of Theorem 1,if multi-agent system(3)achieves guaranteed cost consensus,thenThus,from Definition 1 and(19),one can see that consensus functionc(t)satisfies

Then,by(33)and(34),the conclusions can be obtained.

Remark 3:Theorem 2 shows that the guaranteed cost is related to the initial statesx(0)and the maximum time delayτmax.Moreover,one can see that Corollary 1 implies that the time-varying delay and the guaranteed cost function do not impact on the consensus function.

In Theorem 1,it is difficult to give feasible LM I criteria for obtaining guaranteed cost consensus since there exists nonlinear term(PBKandK T BTW)whenKis unknown.In the sequel,the result presents a design method of the guaranteed cost consensus for multi-agent system(5),where gives an approach to determine the control gain matrix.

Theorem 3:Multi-agent system(2)is said to be guaranteed cost consensualizable by consensus protocol(4)if there existd-dimensional matricesandsuch that

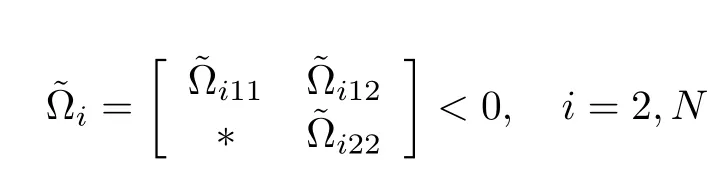
where

In this case,the control gain matrix of multi-agent system(5)satisfiesand the guaranteed cost function has an upper bound

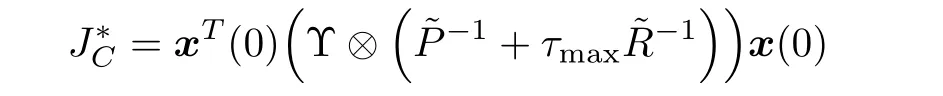
Proof:The method of changing variables is used to determineK.By the Schur complement,Ωi＜0,i=2,Nin Theorem 1 is equivalent to

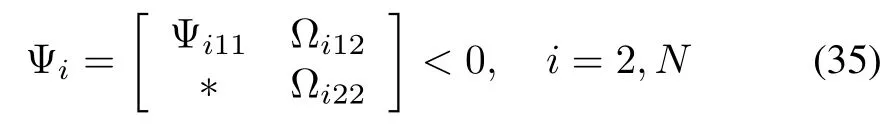
where

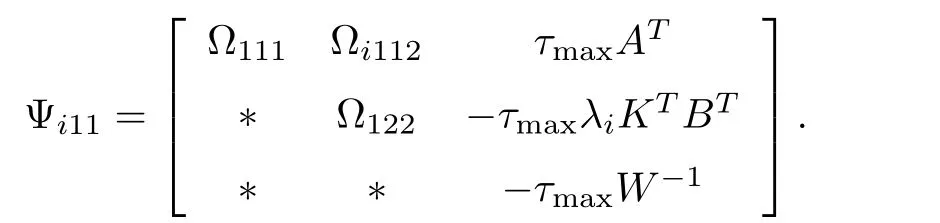
Let

then Ψican be rewritten as

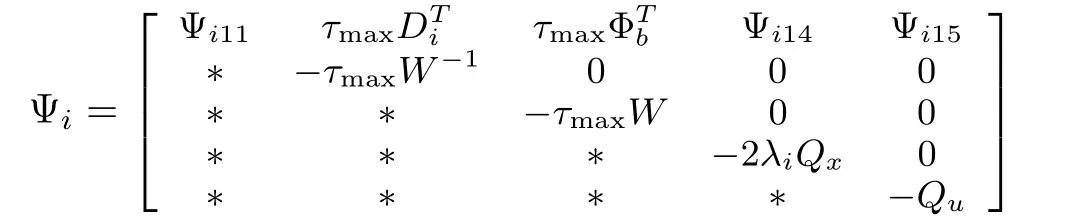
and

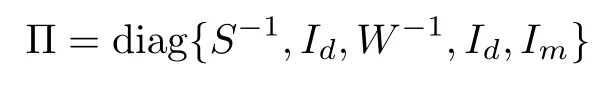
respectively,one has

where

Remark 4:Theorems1 and 3 present the LMI conditions for guaranteed cost consensus and consensualization respectively.The feasibility of these LMI conditions can be checked by using the MATLAB’s LMI Toolbox.

IV.NUMERICAL SIMULATIONS

A high-dimensional multi-agent supporting system is considered,where it is composed of eight agents labeled from 1 to 8.The dynamics of each agent is described as(1)withAandB.In the cost function(6),Qx=0.6I2andQu=0.4 are given.The interaction topologyGis given in Fig.1,where the weights of edges of the interaction topology are 1.Then,it can be obtained thatλ2=0.5858 andλN=4.7321.Let the time varying delay satisfiesτ(t)=0.05+0.04 sin(t),thenτmax=0.09 andℓ=0.04.The simulation step isTs=0.001s.The initial states of all agents are

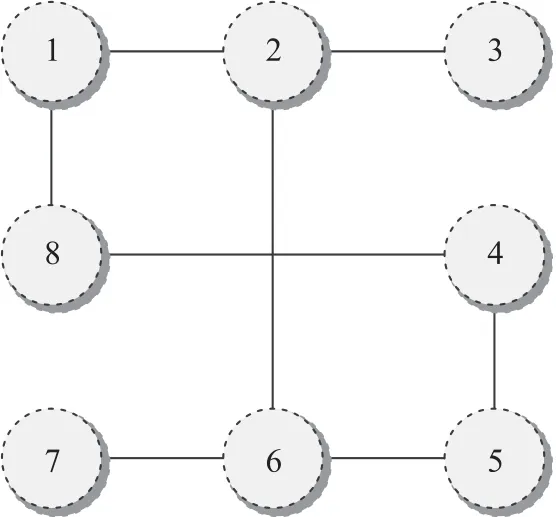
Fig.1. The interaction topology G.

Two cases with different system matrix(A,B)are considered as

Case 1:

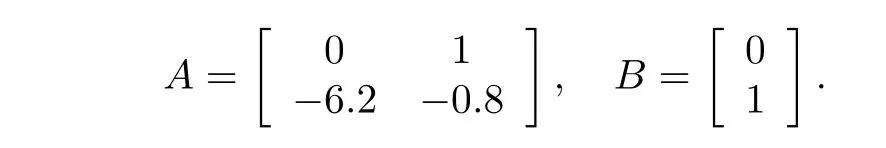
Case 2:

For Case 1,(A,B)are stable.From Theorem 3 andP=it can be obtained thatK=[−0.0019,0.2387]and

In Figs.2 and 3,the state trajectories of the multi-agent system are shown,where the trajectories marked by circles denote the curves of the consensus function obtained by Corollary 1.It is clear that the multi-agent system achieves guaranteed cost consensus.In this case,the guaranteed cost isand the consensus function satisfiesFig.4 shows the trajectories of the cost function.

For Case 2,(A,B)are unstable.Then,one hasK=[−0.2019,0.2839]and

In Figs.5 and 6,the state trajectories of the multi-agent system are shown,and Fig.7 shows the trajectories of the cost function.In this case,and the consensus function satisfies

From the simulation results of Case 1 and Case 2,three aspects should be pointed out.Firstly,one can see that the high-dimensional multi-agent supporting system is able to achieve the guaranteed cost consensus by the proposed approach.Secondly,the runtime may be different when the multi-agent system achieves the guaranteed cost consensus.

Fig.2. Case 1:State trajectories of xi1(t)(i=1,2,...,8).

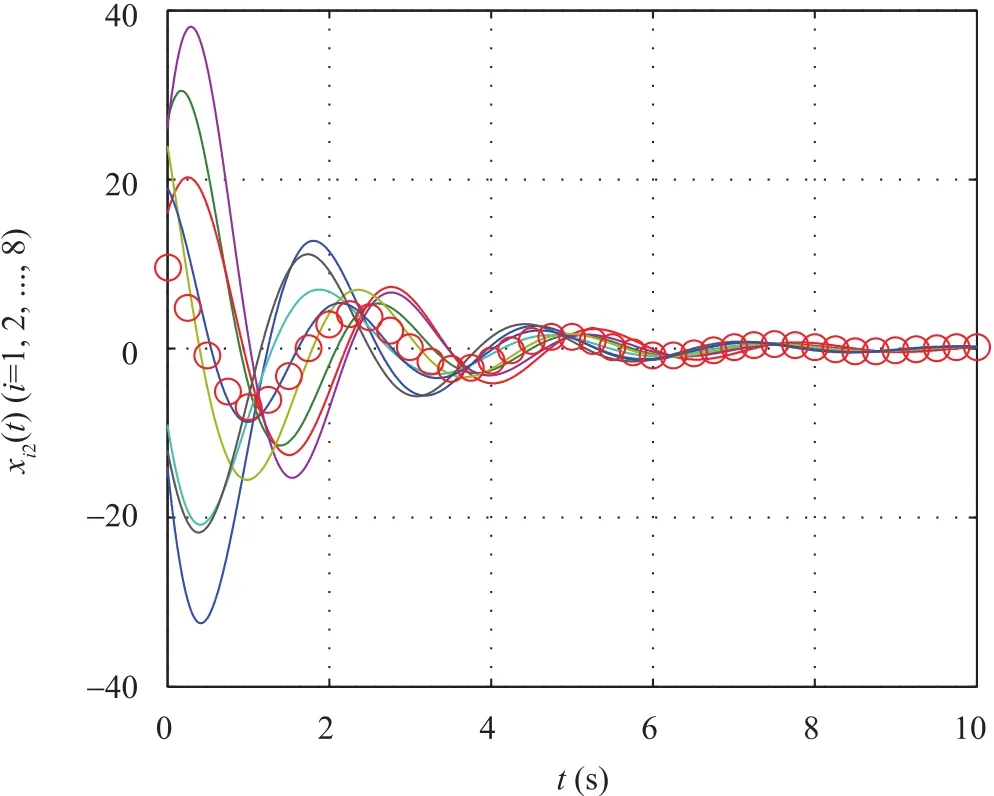
Fig.3. Case 1:State trajectories of xi2(t)(i=1,2,...,8).

Fig.5. Case 2:State trajectories of xi1(t)(i=1,2,...,8).

Fig.6. Case 2:State trajectories of xi2(t)(i=1,2,...,8).

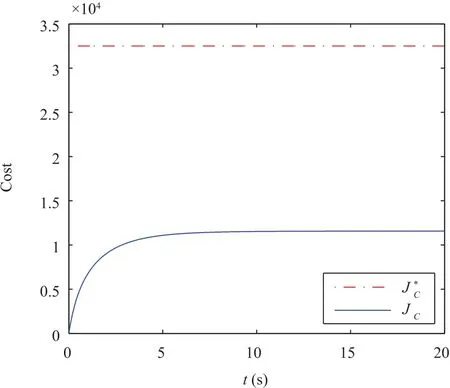
Fig.7. Case 2:Trajectories of the guaranteed cost function.

The runtime of the unstable cases is15s in the above example,while one of the stable cases is 5s.Thirdly,there exists some levels of the conservatism for the guaranteed cost function,where the conservatism can be depicted byandJCis used to represent the actual guaranteed cost.

V.CONCLUSION

The guaranteed cost consensus analysis and design for high dimensional multi-agent systems with time-varying delays were studied in the current paper.In order to simultaneously consider the control effort and consensus errors,guaranteed cost consensus problems for multi-agent systems were introduced.Sufficient conditions for guaranteed cost consensus problems were presented and an upper bound of the cost function was determined.Moreover,the analysis approach in the current paper is based on the fact that the Laplacian matrix is symmetric and only real Laplacian eigenvalues exist,and the Laplacian matrix associated with a directed topology is asymmetric and its nonzero eigenvalues may be complex numbers.In the future,the influence of directed topologies should be deeply studied.

ACKNOWLEDGMENT

The authors would like to thank Minghua Liu for providing numerical analysis and simulation.

[1]K.K.Oh and H.S.Ahn,“Formation control of mobile agents based on distributed position estimation,”IEEE Trans.Automat.Contr.,vol.58,no.3,pp.737−742,Mar.2013.

[2]J.P.He,H.Li,J.M.Chen,and P.Cheng,“Study of consensus-based time synchronization in wireless sensor networks,”ISA Trans.,vol.53,no.2,pp.347−357,Mar.2014.

[3]Z.W.Li,C.Z.Zang,P.Zeng,H.B.Yu,and H.P.Li,“MAS based distributed automatic generation control for cyber-physical microgrid system,”IEEE/CAA J.Automat.Sin.,vol.3,no.1,pp.78−89,Jan.2016.

[4]J.J.Yu,S.M.LaValle,and D.Liberzon,“Rendezvous without coordinates,”IEEE Trans.Automat.Contr.,vol.57,no.2,pp.421−434,Feb.2012.

[5]Y.Z.Sun,Y.J.Wang,and D.H.Zhao,“Flocking of multi-agent systems with multiplicative and independent measurement noises,”Phys.A:Stat.Mech.Appl.,vol.440,pp.81−89,Dec.2015.

[6]Y.C.Cao,W.W.Yu,W.Ren,and G.R.Chen,“An overview of recent progress in the study of distributed multi-agent coordination,”IEEE Trans.Ind.Inform.,vol.9,no.1,pp.427−438,Feb.2013.

[7]R.Olfati-Saber,J.A.Fax,and R.M.Murray,“Consensus and cooperation in networked multi-agent systems,”Proc.IEEE,vol.95,no.1,pp.215−233,Jan.2007.

[8]W.Ren,R.W.Beard,and E.M.Atkins,“Information consensus in multivehicle cooperative control,”IEEE Contr.Syst.Mag.,vol.27,no.2,pp.71−82,Apr.2007.

[9]W.Qiao and R.Sipahi,“Delay-dependent coupling for a multi-agent LTI consensus system with inter-agent delays,”Phys.D:Nonlin.Phenom.,vol.267,pp.112−122,Jan.2014.

[10]J.Z.Liu,H.T.Zhang,J.Liu,and W.C.Xie,“Distributed stochastic consensus of multi-agent systems with noisy and delayed measurements,”IET Control Theory Appl.,vol.7,no.10,pp.1359−1369,Jul.2013.

[11]X.W.Liu,W.L.Lu,and T.P.Chen,“Consensus of multi-agent systems with unbounded time-varying delays,”IEEE Trans.Automat.Contr.,vol.55,no.10,pp.2396−2401,Oct.2010.

[12]R.Olfati-Saber and R.Murray,“Consensus problems in networks of agents with switching topology and time-delays,”IEEE Trans.Automat.Contr.,vol.49,no.9,pp.1520−1533,Sep.2004.

[13]Z.H.Wang,J.J.Xu,and H.S.Zhang,“Consensus ability of multiagent systems with time-varying communication delay,”Syst.Control Lett.,vol.65,pp.37−42,Mar.2014.

[14]P.Lin,M.X.Dai,and Y.D.Song,“Consensus stability of a class of second-order multi-agent systems with nonuniform time-delays,”J.Franklin Inst.,vol.351,no.3,pp.1571−1576,Mar.2014.

[15]W.G.Zhang,J.Z.Liu,D.L.Zeng,and T.T.Yang,“Consensus analysis of continuous-time second-order multi-agent systems with nonuniform time-delays and switching topologies,”Asian J.Control,vol.15,no.5,pp.1516−1523,Sep.2013.

[16]J.H.Qin,H.J.Gao,and W.X.Zheng,“Second-order consensus for multi-agent systems with switching topology and communication delay,”Syst.Control Lett.,vol.60,no.6,pp.390−397,Jun.2011.

[17]Y.Cui and Y.Jia,“L2–L∞consensus control for high-order multiagent systems with switching topologies and time-varying delays,”IET Control Theory Appl.,vol.6,no.12,pp.1933−1940,Aug.2012.

[18]Q.J.Zhang,Y.F.Niu,L.Wang,L.C.Shen,and H.Y.Zhu,“Average consensus seeking of high-order continuous-time multi-agent systems with multiple time-varying communication delays,”Int.J.Control Autom.Syst.,vol.9,no.6,pp.1209−1218,Dec.2011.

[19]P.Lin,Z.Li,Y.Jia,and M.Sun,“High-order multi-agent consensus with dynamically changing topologies and time-delays,”IET Control Theory Appl.,vol.5,no.8,pp.976−981,May2011.

[20]W.Qin,Z.X.Liu,and Z.Q.Chen,“Impulsive observer-based consensus control for multi-agent systems with time delay,”Int.J.Control,vol.88,no.9,pp.1789−1804,Feb.2015.

[21]B.Zhou and Z.L.Lin,“Consensus of high-order multi-agent systems with large input and communication delays,”Automatica,vol.50,no.2,pp.452−464,Feb.2014.

[22]X.Wang,A.Saberi,A.A.Stoorvogel,H.F.Grip,and T.Yang,“Consensus in the network with uniform constant communication delay,”Automatica,vol.49,no.8,pp.2461−2467,Aug.2013.

[23]J.X.Xi,N.Cai,and Y.S.Zhong,“Consensus problems for high-order linear time-invariant swarm systems,”Phys.A:Stat.Mech.Appl.,vol.389,no.24,pp.5619−5627,Dec.2010.

[24]S.Hu,X.Yin,Y.Zhang,and E.G.Tian,“Event-triggered guaranteed cost control for uncertain discrete-time networked control systems with time-varying transmission delays,”IET Control Theory Appl.,vol.6,no.18,pp.2793−2804,Dec.2012.

[25]Y.Y.Wang,Q.B.Wang,P.F.Zhou,and D.P.Duan,“Robust guaranteed cost control for singular Markovian jump systems with time-varying delay,”ISA Trans.,vol.51,no.5,pp.559−565,Sep.2012.

[26]S.Chang and T.Peng,“Adaptive guaranteed cost control of systems with uncertain parameters,”IEEE Trans.Automat.Contr.,vol.17,no.4,pp.474−483,Aug.1972.

[27]Z.Wang,J.X.Xi,Z.Y.Yu,and G.B.Liu,“Guaranteed cost consensus for multi-agent systems with time delays,”J.Franklin Inst.,vol.352,no.9,pp.3612−3627,Sep.2015.

[28]Z.Wang,J.X.Xi,Z.C.Yao,and G.B.Liu,“Guaranteed costconsensus for multi-agent systems with fixed topologies,”Asian J.Control,vol.17,no.2,pp.729−735,Mar.2015.

[29]Z.Wang,J.X.Xi,Z.C.Yao,and G.B.Liu,“Guaranteed cost consensus for multi-agent systems with switching topologies,”Int.J.Robust Nonlin.Control,vol.25,no.16,pp.3099−3112,Nov.2015.

[30]Z.H.Guan,B.Hu,M.Chi,D.X.He,and X.M.Cheng,“Guaranteed performance consensus in second-ordermulti-agent systems with hybrid impulsive control,”Automatica,vol.50,no.9,pp.2415−2418,Sep.2014.

[31]Y.Cheng and V.Ugrinovskii,“Leader-follower tracking control with guaranteed consensus performance for interconnected systems with linear dynamic uncertain coupling,”Int.J.Control,vol.88,no.8,pp.1633−1677,Feb2015.

[32]X.J.Zhou,P.Shi,C.C.Lim,C.H.Yang,and W.H.Gui,“Event based guaranteed cost consensus for distributed multi-agent systems,”J.Franklin Inst.,vol.352,no.9,pp.3546−3563,Sep.2015.

[33]C.Godsil and G.Royle,Algebraic Graph Theory.New York:Springer-Verlag,2001.

[34]X.M.Zhang,M.Wu,J.H.She,and Y.He,“Delay-dependent stabilization of linear systems with time-varying state and input delays,”Automatica,vol.41,no.8,pp.1405−1412,Aug.2005.

[35]R.A.Horn and C.R.Johnson,Matrix Analysis.Cambridge:Cambridge University Press,1990.