Distributed Tracking Control of a Class of Multi-agent Systems in Non-affine Pure-feedback Form Under a Directed Topology

Yang Yang and Dong Yue,

I.INTRODUCTION

T HE consensus problem of multi-agent systems(MASs)has received compelling interest and has been studied extensively in the cybernetics community,over the past decade,due to their industrial applications in formation control of surface vehicles,cooperative control of mobile robots,distributed sensor networks,and so on[1]−[9].Distributed control methods are capable to coordinate the behavior by transmitting/receiving information to/from other neighboring agents,and the advantages imposed by this configuration include modularity,scalability and robustness[10].Consensus control problems of first-order MASs were reported in[5]and[11].The relevant research work were extended to a leader-follower multi-agent system with measurement noises in[12]and a leader escort problem in[13].Then,consensus protocols for second-order MASs and general linear systems were appeared in[14]−[17].Kimetal.considered the output consensus problem for a class of heterogeneous uncertain linear multi-agent systems in[18].However,systems in practice are usually with nonlinear dynamics due to unpredictable environmental disturbances,unmodelled dynamics or other uncertainties[19]−[22].In[23],Wanget al.investigated the consensus problem for heterogeneous agents with nonlinear dynamics in a directed communication network by employing a quadratic Lyapunov function and linear matrix inequalities.Dong and Huang considered an output regulation problem for arbitrary relative degree nonlinear MASs with trivial zerodynamics in[24].A distributed adaptive nonlinear control law was constructed by the backstepping method in[25].A tracking consensus approach for MASs in strict-feedback form with mismatched unknown parameters was reported in[26]and tracking scheme for the agents in semi-strictfeedback dynamics form was discussed in[27].As a result,a common disadvantage of the work in[25]−[27]was that the computational burdens increased drastically with the grow th of the order of the system because of repeated differentiations of immediate control signals inherent in the conventional backstepping method[28].Fortunately,a dynamic surface control(DSC)technique was proposed by Swaroopet al.in[29].The main idea of this technique was to take the place of differentiation computations by a first-order filter at each step.On the basis of this idea,effective efforts were made to combine this technique with neural networks(NNs)[30],wavelet NNs[31],and fuzzy logic systems[32].And then it was applied to control of several classes of nonlinear systems,such as single-input-single-output(SISO)systems in[33],[34],multiple-input-multiple-output(M IMO)systems in[35],[36],MASs in[37],[38],and so on.

It is noted that most of the reported results of consensus problem are developed for MASs with the homogeneous dynamics.Until recently,effective efforts have been taken to develop control methodologies for MASs consisting of heter-ogeneous agents.In[39],[40],consensus protocols were proposed for linear systems.An output control method was studied for a class of heterogeneous uncertain linear MASs in[18].And then the work in[18]was extended to more general cases in[41].For discrete-time heterogeneous multi-agent systems,the consensus issue with event-triggered scheme was investigated in[42].Output consensus problem of heterogeneous discrete-time MASs in presence of uncertainties and disturbances was reported in[43].

Motivated by the above mentioned analysis,we focus our attention to consensus tracking for heterogeneous MASs in non-affine pure-feedback form under a directed topology.In detail,this class of nonlinear MASs is transformed into the strict-feedback form with the aid of the function transformation and uncertain dynamics are approximated by NNs.Also,a first-order low-pass filter is exploited to replace differential operations at each step.The contributions of this paper are mainly summarized as below.1)First of all,unlike previous work in[25],[37],[38],[44],we extend the structure of individual agent to the heterogeneous non-affine pure-feedback form.It is nontrivial to be concentrated on the extension of the presented results to such form,which treats linearly parameterized and affine pure-feedback ones as special cases.2)In addition,uncertainties of the system are taken into account and precise know ledge about system parameters are not required since neural networks are employed to compensate unknown dynamics.3)Last but not the least,compared with the existing work in[26],[27]where control laws were studied based on traditional backstepping methods,the DSC technique is introduced during the design procedure and the shortcoming,the complexity grow th problem along with the increase of the degree and number of agents,is overcome.It leads to a much simpler and more practical control scheme.

The remainder of this paper is organized as follows.In Section II,we formulate the problem under discussion and review some necessary preliminaries;whereas Section III provides main results,including a design procedure for the proposed controller,as well as the closed-loop stability analysis.In Section IV,two simulation examples are presented to validate the effectiveness of the control.Finally,conclusions are drawn in Section V.

Notations:Letλmax(·)be maximum eigenvalue of a matrix.|·|stands for the absolute value of a scalar.‖ ·‖means Euclidean norm of vectors or induced norm of matrices.⊗represents Kronecker product.

II.PROBLEM FORMULATION AND PRELIMINARIES We consider a class of MASs composed of one leader andNfollowers in a directed topology,and the dynamics of theith follower are described as

Remark 1:Compared with the results in[25],[37],[38],[44],we restrict our attention to a more generalized system with non-affine pure-feedback architecture rather than especial cases in strict-feedback form.Accordingly,it is formidable to construct explicit virtual controls and the stability analysis is more challenging and complex since control signals are not of affine appearance and it might result in algebraic loop problem.In practice,the general form is applicable to describe several physical plants,such as biochemical processes,robotic manipulators,unmanned surface vehicles and so on[28].We are interested in the control design for system(1)directly,which is not only academically challenging but also of practical interest.

We consider the leader and followers are connected through a directed topologyG={V,E}whereV={υ0,υ1,...,υN}andE={(υi,υj)∈V×V}are used to represent a node set and an edge set,respectively.(υi,υj)denotes that nodeican obtain information from nodej,but not vice versa.The neighboring set of nodeiis defined asN i.A diagonal matrixB=diag[b1,...,bN]is introduced to represent the accessibility of the leader to the nodei,wherebi=1,if possible;andbi=0,otherwise.Further,a subgraphis used to express the interconnection among follower agents,whereandis the Laplacian matrix of the subgraph,where∈RN×N,aij=1 ifotherwise,andThe more details can be found in[37],[45]and references therein.

The control objective of this paper is to construct a distributed tracking control method for(1)to force the outputyiof followers to synchronize with the desired trajectory of the leaderydunder a directed graph while the tracking errors are cooperatively semi-globally uniformly ultimately bounded(CSUUB).The definition about CSUUB is given as follows.

Definition 1[37]:The distributed consensus tracking errors for followers with nonlinear dynamics(1)under the communication graph are said to be CSUUB if there exist adjustable constantsc1＞0,c2＞0,and the boundsβ1＞0,β2＞0,independent oft0,and for everyα1∈(0,c1)andα2∈(0,c2),there is a timeT≥0,independent oft0,such that‖yi(t0)−yd(t0)‖≤α1⇒‖yi(t)−yd(t)‖≤β1and‖yi(t0)−yj(t0)‖≤α2⇒‖yi(t)−yj(t)‖≤β2,for allt≥t0+Twherei=1,...,N,j=1,...,N,i/=j.

The preliminaries about the radial basis function(RBF)neural networks are omitted due to space limitation.In the rest of the paper,andare unknown ideal constant weight vectors,ϕi,j(Zi,j)andGi(Zi)are Gaussian function vectors with appropriate dimensions and corresponding input vectorsZi,jandZiwill be given later.Interested readers may refer to[46],[47]for more details.

The following assumption is necessary to be introduced.

Assumption 1:The trajectory signal of the leaderydis smooth andyd,˙yd,ÿdare bounded,that is to say,there exists a positive constant%i0satisfying that

Remark 2:In practice,the energy of command generators are limited.In this case,Assumption 1 is substantially common and it can also be found in existing literature,such as[33].

III.CONTROL LAW DESIGN AND STABILITY ANALYSIS

In this section,a distributed adaptive consensus tracking scheme for system(1)will be designed recursively by the backstepping approach,the DSC technology and NNs approximators to achieve the control objective stated in Section II.And the stability analysis of the whole system will be expatiated in the following paragraph.

A.Control Law Design

For theith agent(1),let

wherei=1,...,N,j=1,...,ni−1.

It follows that,from(2)and(3),

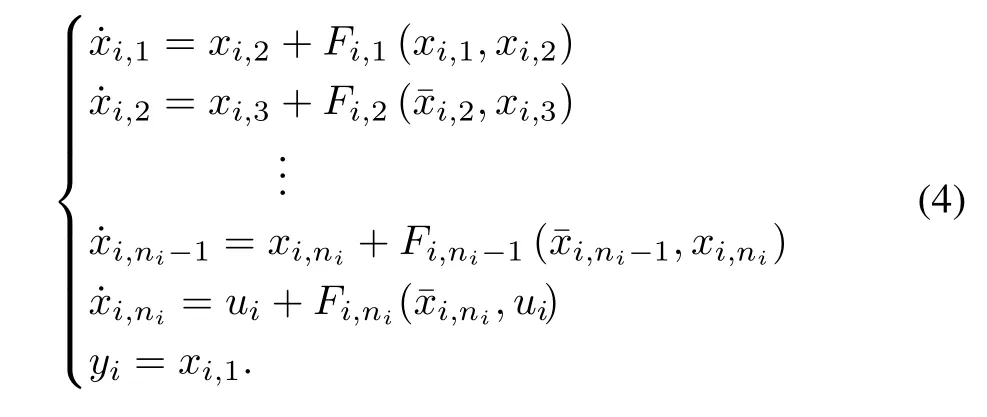
To circumvent the problem of the algebraic loop mentioned in[48],[49],xi,j,fandui,f,motivated by[50],are defined as the filtered signals

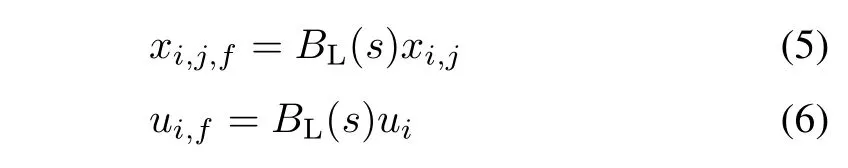
whereBL(s)is a Butterwoth low-pass filter(BLF).In[48],corresponding parameters of the filter whose cutoff frequencieswc=1 rad·s−1are listed for different filter order.To move on,the following assumptions are needed.

Assumption 2:For∀M1∈Rjand∀M2∈Rj,there exist known constantsm i,jsatisfying

wherei=1,...,N,j=1,...,ni.

Assumption 3:There exist positive constantsbi,j,0andbi,n i+1,0,such that

Remark 3:Since most physical actuators exhibit low-pass properties in a sense,the replacementsandui,fare reasonable in the control strategy design procedure.Assumption 3 is not very serious,and readers may refer relevant results in[48]−[50].

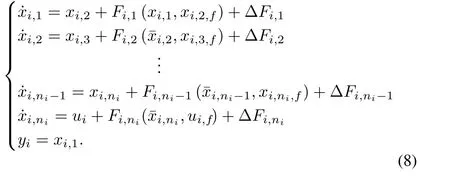
Define

wherezi,jis the immediate signal to be expounded later,i=1,...,N,j=2,...,ni.

Stepi,1:From(8)and(9),the derivative ofsi,1is computed as

Choose the virtual control lawαi,2as

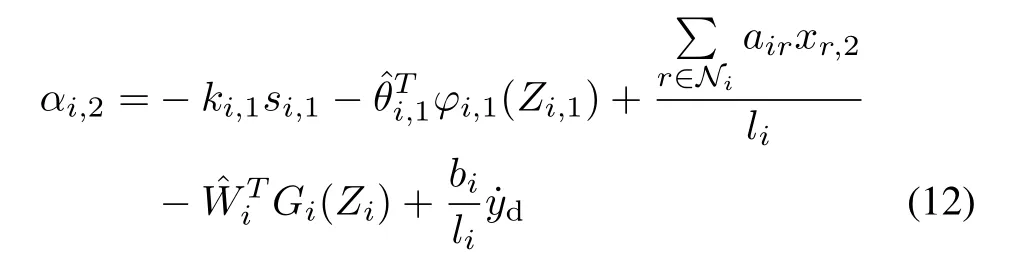
whereki,1＞0,NNsandare employed to approximate unknown functionsandrespectively.

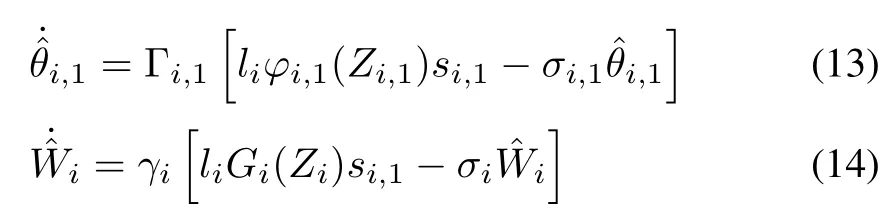
whereςi,2is the time constant of the filter.

Stepi,j(2≤j≤ni−1):Noting(8)and(10),we have

Accordingly,the virtual control lawαi,j+1can be taken as

with the adaptive law

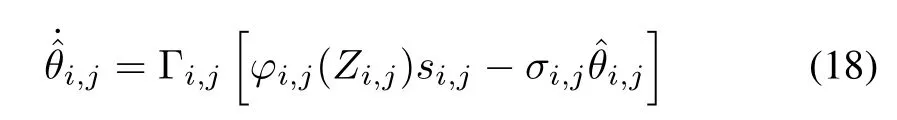
where

Similarly,letαi,j+1pass through a first-order filter

whereςi,j+1＞0.

Stepi,ni:The final control law for theith agent will be derived in this step.For the surface errorsi,ni=xi,ni−zi,ni,we have

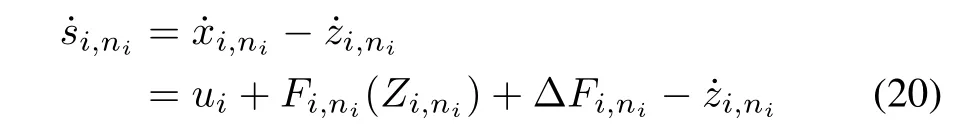
The control law is chosen as

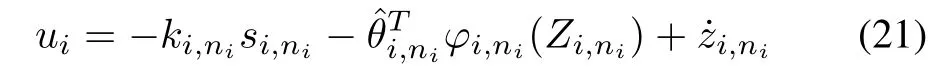
with the adaptive law

where

Remark 4:In the above design procedure,it should be emphasized that no differentiation of virtual controls have to be performed while the method introduced in[26]and[27]might result in heavy calculation burden along with drastic grow th of the degree of individual followers.Moreover,this problem seems more severe in the scenario in which the MASs contain a large number of followers.Compared with the structures of controller in[26]and[27],the proposed control law in this paper just carries out simple algebraic operations instead of repeated derivation calculations about the virtual control signals at each intermediate step in the sense of the DSC approach.It is further use of embedded microprocessors with alleviative calculation burden for individual agents,and this is preferable for industrial applications.

B.Stability Analysis

Letand considering(19),˙zi,j+1can be further written as

wherei=1,...,N,j=1,...,ni−1.

By noting(12)and(15),the equation follows

whereBi,2(·)is a continuous function.Similarly,forj=2,...,ni−1.

whereBi,j+1(·)is a continuous function.

The main result can be summarized in the following theorem.

Theorem 1:Consider a group of agents(1)under a directed graph satisfying Assumptions 1−3.Then,for bounded initial conditions,the output tracking errors are CSUUB and can converge to a small neighborhood around the origin by the control law and adaptive laws composed of(13),(14),(18),(21)and(22)with appropriate design parameters.

Proof:Defin,and choose the following Lyapunov function candidate for theith agent

DifferentiatingViyields

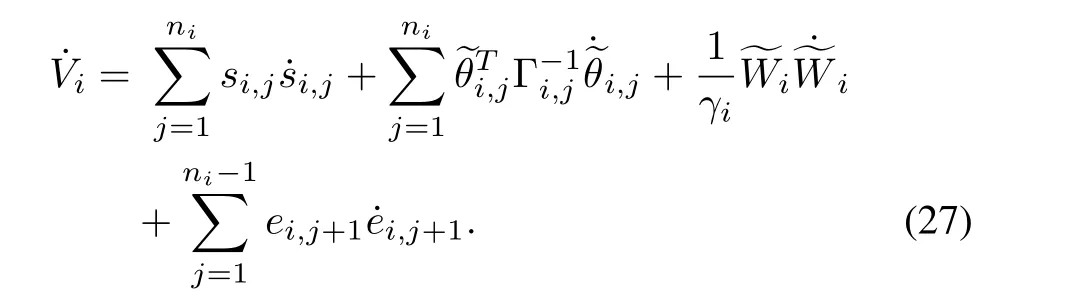
From Assumptions2 and 3,and the fact that,the following inequalities hold

(27)can be rewritten as

Since

and denoting

inequality(33)can be further written as

Chooseand its derivative is

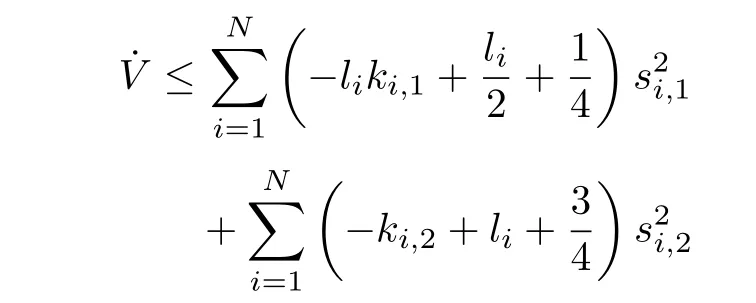
where

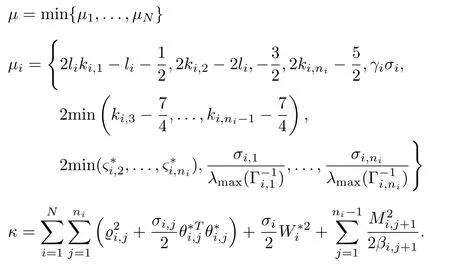
which indicates thatV(t)is uniformly ultimately bounded.Accordingly,signalsandei,lare bounded,l=2,...,ni,thenαi,l,zi,landxi,j,l=2,...,ni,j=2,...,ni,are also bounded.Because of the boundedness ofydmentioned in Assumption 1,the fact follows thatxi,1is bounded.Consequently,the signalsandare bounded by virtue of

From(39),one has(39)and unknown constantsTherefore,all signals in the closed-loop system remain bounded,fori=1,...,N,j=1,...,ni.

By virtue of(40),we deduce that

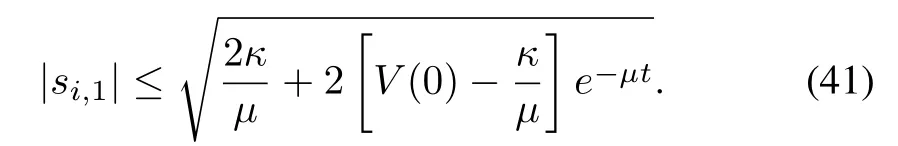
It implies that,as time increases,the tracking errorconverge to the compact setand the error can be made arbitrarily small by the suitable design parameters.Further,in light of the fact thatand Remark 1 in[37],whereis aN-vector of all ones,it means that the consensus tracking errorsare bounded and can be reduced.

IV.SIMULATION EXAMPLES

In order to illustrate the design procedure and the control performance of the proposed method,we present the following two simulation examples.

A.Example A

Taking a practical system of a group of one-link manipulators described in[51]as the first example.The dynamics ofith one are described as

whereandVirepresent angular position,velocity,acceleration,motor current and input voltage,respectively.And the parameters areD i=1,B i=1,N i=10,M i=0.05,H i=0.5 andKm,i=10.By notingxi,1=qi,xi,2=˙qi,xi,3=Iiandui=Vi,the above equation can be expressed in the form(1)as

where3.The output signals of three followers are forced to synchronize with the leader’s,that is,and the communication topology is shown in Fig.1.The initial conditions arex1,1(0)=−0.3,x1,2(0)=0.5π,x1,3(0)=0.0,x2,1(0)=−0.15,x2,2(0)=0.5π,x2,3(0)=0.0,x3,1(0)=−0.1,x3,2(0)=0.5π,x3,3(0)=0.0.The design parameters are chosen ask1,1=5,k1,2=4,k1,3=4,k2,1=5,k2,2=4,k2,3=4,k3,1=5,k3,2=4,k3,3=10,Γi,j=3IlNN×lNN,σi,j=1.5,ςi,p=0.1,i=1,2,3,j=1,2,3,p=1,2,wherelNN=15 is node number of the hidden layer for each neural network with centers of Gaussian functions evenly spaced in[−1,1].The initial values of neural weight estimation arej=1,2,3.Simulation results are given in Figs.2−9.Fig.3 and Figs.4−6 show control input signals and state variables,respectively.Responses of the norms of adaptive parameters are shown in Figs.7−9.

Fig.1.Communication graph for Example A.

In order to illustrate the relationship between control performance and control gains,we give the definition of the tracking error,errori=yi−yd,and consider the following three cases in Table I,where initial conditions and other parameters are the same as before.Takingerror2as an example,the dynamics of it in three cases are depicted in Fig.10.Comparing the tracking results,it can be observed that the steady-state tracking errors decrease aski,jare scaled up.Alternatively,inverse behaviors can be obtained if we scale downki,j.

Fig.2.Output trajectories of the followers with one leader.

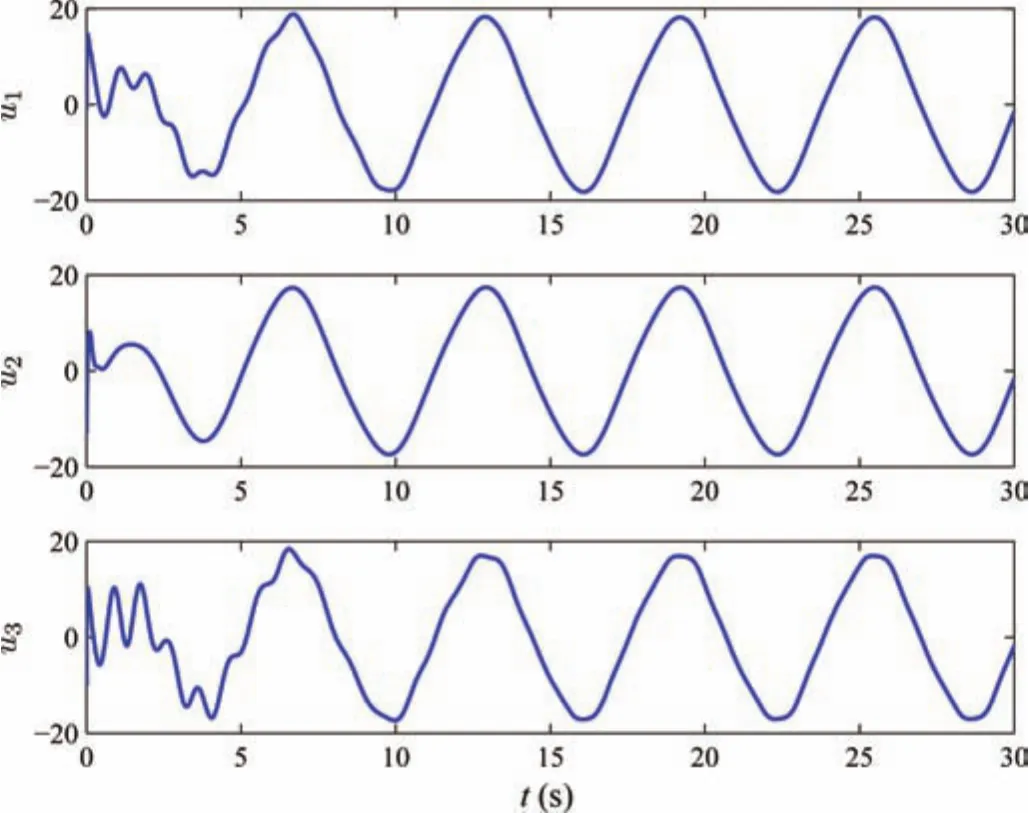
Fig.3. Control input signals.

Fig.4. State variables x1,2 and x1,3.

Fig.5. State variables x2,2 and x2,3.

Fig.6. State variables x3,2 and x3,3.

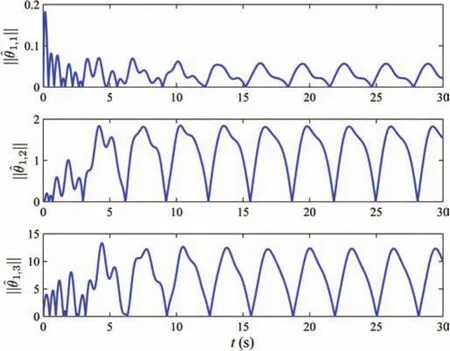
Fig.7.The norms of adaptive parameters

Fig.8.The norms of adaptive parameters

Fig.9.The norms of adaptive parameters

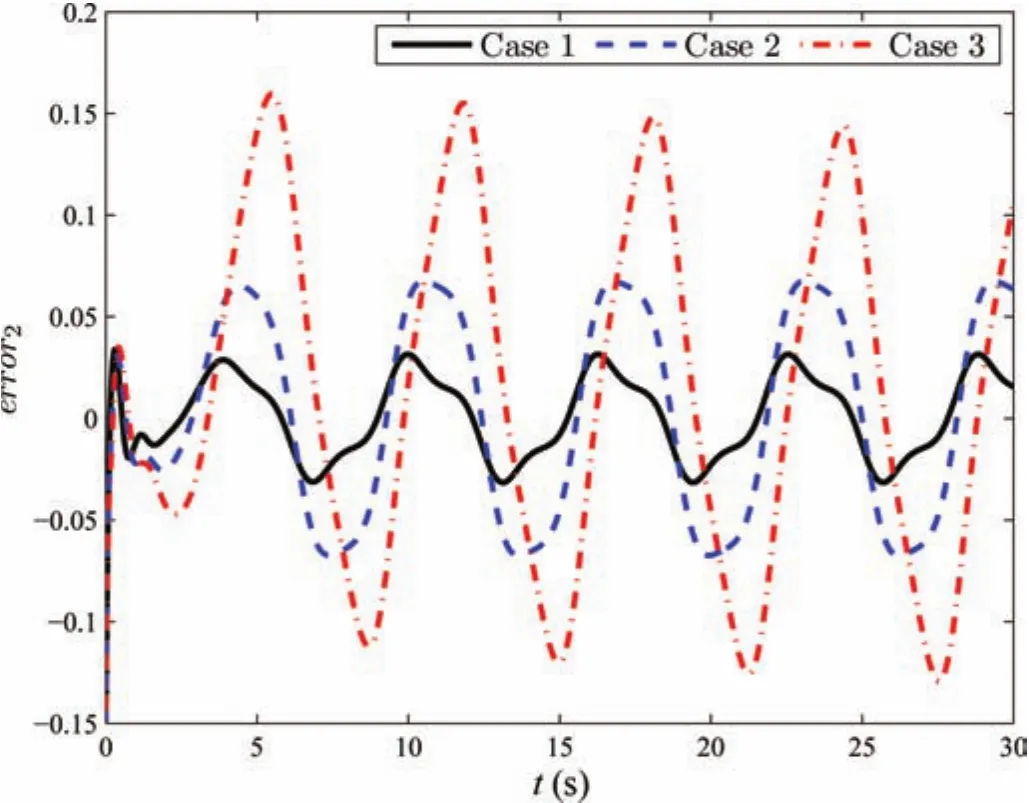
Fig.10.Comparison of tracking performances.

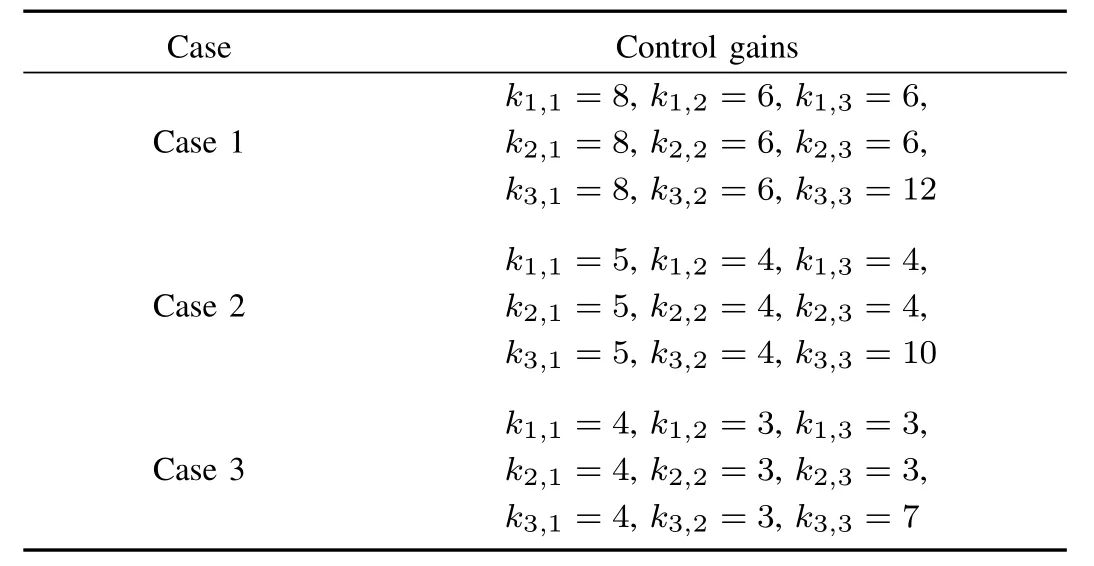
TABLE I CONTROL GA INS IN THREE CASES

Remark 1:From the proof analysis in Section IV,the transient and steady state tracking errors can be made smaller by suitable choice of the control gainski,j.From(41),it indicates that the inverse relationship exists between the size of the steady state compact set and the parameterski,jsinceµtends to increase as control gains are scaled up.However,it should be pointed out very large control gains would lead to unexpected large control input signals at the initial stage,which is not permissible from a practical point of view.These suggest intuitive tuning procedures for the control gains.

To further compare the computation complexity between the DSC approach and the backstepping approach,we list simulation times and the corresponding execution times in Table II,where all the cases are in the same conditions.From Table II,it indicates that the former one undergoes less program execution time than the latter’s;that is because of the inherent computation burden,i.e.,repeated differentiation operations,in the latter method.

TABLE II COMPARISON OF PROGRAM EXECUTION TIME

B.Example B

In the foregoing practical example,it is noted that the follower agents are in the same order and gain functions are constant,which can be viewed as a special case of the system(1).Next,we consider a group of four followers with one leader denoted as 0,and the fourth one is in non-affine purefeedback heterogeneous form.They are connected through the following digraphG2as shown in Fig.11.The dynamics of followers 1,2 and 3 are

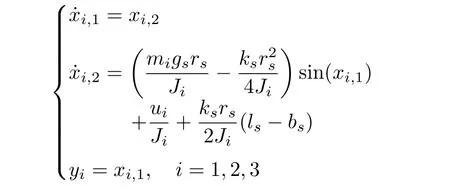
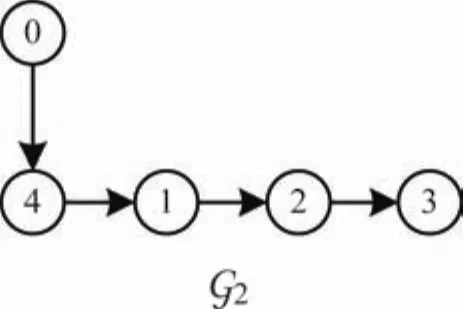
Fig.11.Communication graph for Example B.

and of the fourth one are

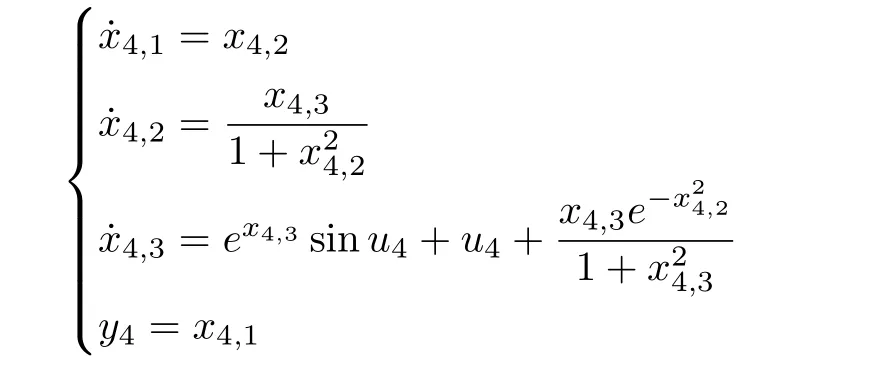
wherex1,1,x1,2,x2,1,x2,2,x3,1,x3,2,x4,1,x4,2andx4,3are state variables,u1,u2,u3andu4are input signals,y1,y2,y3andy4are outputs of follower agents,gs=9.8,rs=0.5,ks=10,ls=0.5,bs=0.4,m i=0.2,Ji=0.5,i=1,2,3.The trajectory of the leaderyd=0.5sin(0.5t)+0.5sin(t).We choose each neural network containsl=15 nodes and Gaussian functions with centers evenly spaced in[−1,1],respectively.The design parameters are taken ask1,1=2,k1,2=10,k2,1=2,k2,2=10,k3,1=2,k3,2=10,k4,1=4,k4,2=15,k4,2=5, Γi,j=3Il×l, Γ4,1=3Il×l,Γ4,2=2Il×l,Γ4,3=3Il×l,γi=3Il×l,γ4=3Il×l,σi,j=σi=1.5,σ4,1=σ4,2=σ4,3=σ4=1.5,ςi,2=0.1,ς4,3=0.1,i=1,2,3,j=1,2.The initial conditions arex1,1(0)=0.5,x1,2(0)=0.0,x2,1(0)=0.3,x2,2(0)=0.0,x3,1(0)=0.2,x3,2(0)=0.0,x4,1(0)=0.1,x4,2(0)=0.01,andx4,3(0)=0.01,and the initial values of neural weight estimation areˆθi,j(0)=ˆθ4,3(0)=ˆW i(0)=01×l,i=1,2,3,4,j=1,2.Simulation results are shown in Figs.12−22.Output trajectories of the followers with one leader and tracking errors,denoted aserrori=yi−yd,i=1,2,3,4,are depicted in Figs.12 and 13,respectively.It can be seen that the tracking errors converge to around zero as time increases,and it should be noted that the tracking performance of neighboring followers is better.Control input signals and state variables are shown in Figs.14−15 and Figs.16−17,respectively.Profiles of the norms of adaptive parameters are depicted in Figs.18−22.Obviously,all signals in the closed-loop system are bounded.The contribution of neural networks is illustrated by comparing the designed adaptive control scheme in this paper with conventional methods without uncertainty approximation.The two cases are with the same conditions and parameters.Tracking errors are denoted aserrorianderrori,cmp,respectively.Taking the first agent and third one for example,in Fig.23,we can observe that the proposed controller forces the tracking errors be smaller and performance better since NNs provide adequate compensation for uncertain dynamics.

V.CONCLUSION

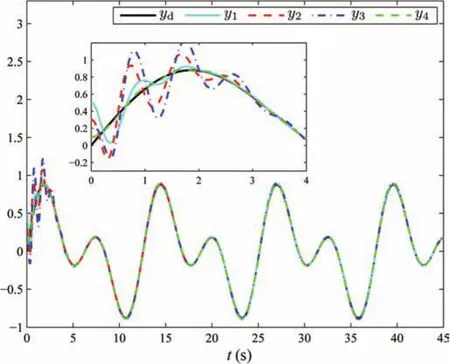
Fig.12.Output trajectories of the followers with one leader.

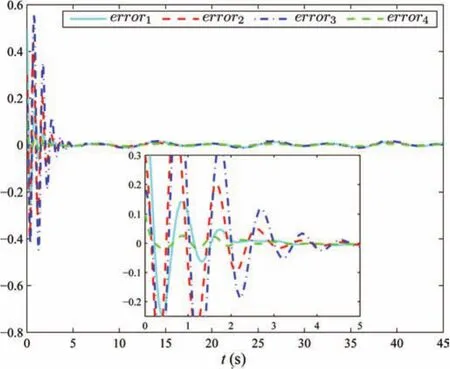
Fig.13.Tracking errors of the followers.

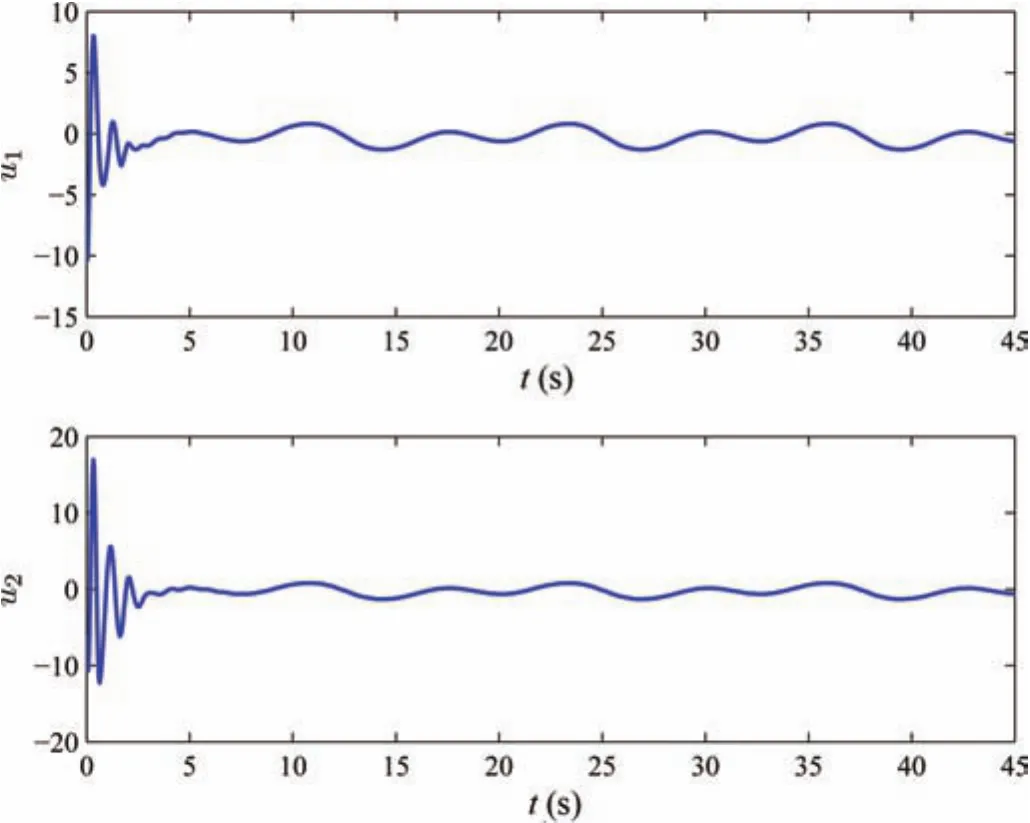
Fig.14.Control input signals u1 and u2.

Fig.15.Control input signals u3 and u4.

Fig.16. State variables x1,2 and x2,2.

Fig.17. State variables x3,2,x4,2 and x4,3.

Fig.18.The norms of adaptive parameters

Fig.19.The norms of adaptive parameters

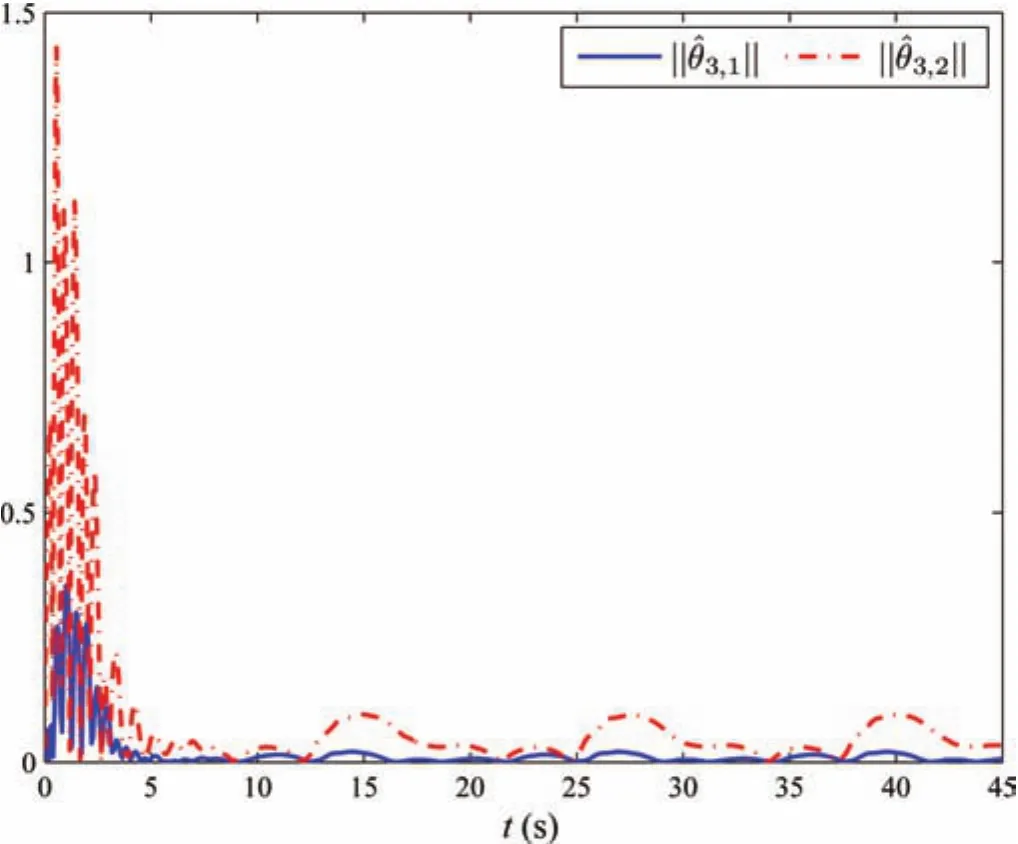
Fig.20.The norms of adaptive parameters

Fig.21.The norms of adaptive parametersand

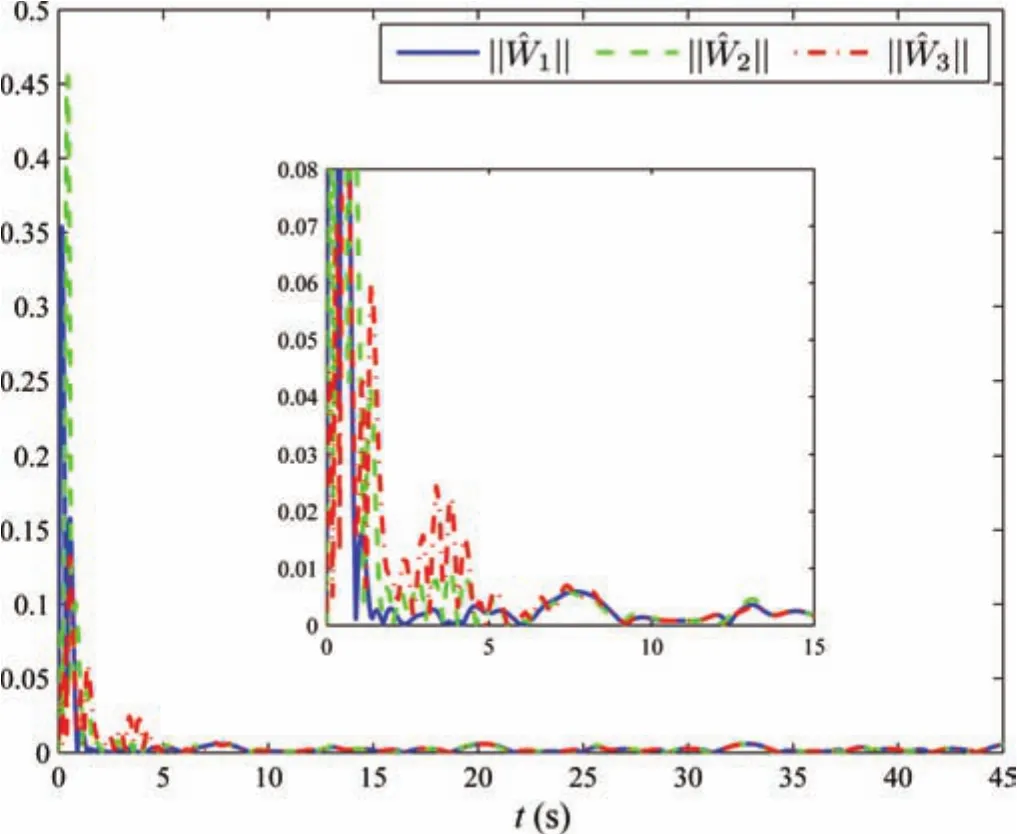
Fig.22.The norms of adaptive parameters

Fig.23.Performance comparison of tracking errors.

We have investigated the consensus tracking problem for MASs in non-affine pure-feedback form under a directed graph in the presence of one leader.The adaptive distributed control strategy is constructed by employing the backstepping approach,DSC technology and NNs approximators.It has been proven that all signals in the closed-loop system are bounded,and the simulation results are provided to illustrate the effectiveness of the proposed control strategy.The extension of this approach to system states with constraints[52],[53]and time-varying switching topologies deserves further research[10].Moreover,considerable effort is to be devoted to cases where networks are subject to delays,data packet dropouts,energy efficiency[54];these issues are critical from an industrial application point of view.

[1]Y.C.Cao,W.W.Yu,W.Ren,and G.R.Chen,“An overview of recent progress in the study of distributed multi-agent coordination,”IEEE Trans.Industr.Inform.,vol.9,no.1,pp.427−438,Feb.2013.

[2]L.Ding,Q.L.Han,and G.Guo,“Network-based leader-following consensus for distributed multi-agent systems,”Automatica,vol.49,no.7,pp.2281−2286,Jul.2013.

[3]G.Guo,L.Ding,and Q.L.Han,“A distributed event-triggered transmission strategy for sampled-data consensus of multi-agent systems,”Automatica,vol.50,no.5,pp.1489−1496,May2014.

[4]W.L.He,B.Zhang,Q.L.Han,F.Qian,J.Kurths,and J.D.Cao,“Leader-following consensus of nonlinear multiagent systems with stochastic sampling,”IEEE Trans.Cybern.,vol.47,no.2,pp.327−338,Feb.2017.

[5]H.W.Zhang,F.L.Lew is,and Z.H.Qu,“Lyapunov,adaptive,and optimal design techniques for cooperative systems on directed communication graphs,”IEEE Trans.Ind.Electron.,vol.59,no.7,pp.3026−3041,Jul.2012.

[6]Z.H.Peng,D.Wang,H.W.Zhang,and G.Sun,“Distributed neural network control for adaptive synchronization of uncertain dynamical multiagent systems,”IEEE Trans.Neural Netw.Learn.Syst.,vol.25,no.8,pp.1508−1519,Aug.2014.

[7]D.M.Yuan and D.W.C.Ho,“Randomized gradient-free method for multiagent optimization over time-varying networks,”IEEE Trans.Neural Netw.Learn.Syst.,vol.26,no.6,pp.1342−1347,Jun.2015.

[8]K.C.Cao,B.Jiang,and D.Yue,“Distributed consensus of multiple nonholonomic mobile robots,”IEEE/CAA J.of Autom.Sinica,vol.1,no.2,pp.162−170,Apr.2014.

[9]J.Huang,H.Fang,L.H.Dou,and J.Chen,“An overview of distributed high-order multi-agent coordination,”IEEE/CAA J.of Autom.Sinica,vol.1,no.1,pp.1−9,Jan.2014.

[10]X.H.Ge,F.W.Yang,and Q.L.Han,“Distributed networked control systems:a brief overview,”Inform.Sciences,vol.380,pp.117−131,Feb.2017.

[11]R.Olfati-Saber,“Flocking for multi-agentdynamic systems:algorithms and theory,”IEEE Trans.Automat.Contr.,vol.51,no.3,pp.401−420,Mar.2006.

[12]J.P.Hu and G.Feng,“Distributed tracking control of leader-follower multi-agent systems under noisy measurement,”Automatica,vol.46,no.8,pp.1382−1387,Aug.2010.

[13]Y.Q.Zhang and Y.G.Hong,“Distributed control design for leader escort of multi-agent systems,”Int.J.Control,vol.88,no.5,pp.935−945,May2015.

[14]Z.Y.Meng,Z.Y.Zhao,and Z.L.Lin,“On global leader-following consensus of identical linear dynamic systems subject to actuator saturation,”Syst.Control Lett.,vol.62,no.2,pp.132−142,2013.

[15]X.L.Liu,B.G.Xu,and L.H.Xie,“Distributed tracking control of second-order multi-agent systems under measurement noises,”J.Syst.Sci.Complex.,vol.27,no.5,pp.853−865,Oct.2014.

[16]L.P.Mo,Y.G.Niu,and T.T.Pan,“Consensus of heterogeneous multi-agent systems with switching jointly-connected interconnection,”Physica A,vol.427,pp.132−140,Jun.2015.

[17]Z.H.Wu,H.J.Fang,and Y.Y.She,“Weighted average prediction for improving consensus performance of second-order delayed multiagent systems,”IEEE Trans.Syst.Man Cybern.BCybern.,vol.42,no.5,pp.1501−1508,Oct.2012.

[18]H.Kim,H.Shim,and J.H.Seo,“Output consensus of heterogeneous uncertain linear multi-agent systems,”IEEE Trans.Automat.Contr.,vol.56,no.1,pp.200−206,Jan.2011.

[19]H.W.Zhang and F.L.Lew is,“Adaptive cooperative tracking control of higher-order nonlinear systems with unknown dynamics,”Automatica,vol.48,no.7,pp.1432−1439,Jul.2012.

[20]S.El-Ferik,A.Qureshi,and F.L.Lew is,“Neuro-adaptive cooperative tracking control of unknown higher-order affine nonlinear systems,”Automatica,vol.50,no.3,pp.798−808,Mar.2014.

[21]W.W.Yu,G.R.Chen,M.Cao,and J.Kurths,“Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics,”IEEE Trans.Syst.Man Cybern.BCybern.,vol.40,no.3,pp.881−891,Jun.2010.

[22]C.L.P.Chen,G.X.Wen,Y.J.Liu,and F.Y.Wang,“Adaptive consensus control for a class of nonlinear multiagent time-delay systems using neural networks,”IEEE Trans.Neural Netw.Learn.Syst.,vol.25,no.6,pp.1217−1226,Jun.2014.

[23]L.Wang,W.Feng,M.Chen,and Q.Wang,“Global bounded consensus in heterogeneous multi-agent systems with directed communication graph,”IET Contr.Theory Appl.,vol.9,no.1,pp.147−152,Jan.2015.

[24]Y.Dong and J.Huang,“Cooperative global output regulation for a class of nonlinear multi-agent systems,”IEEE Trans.Automat.Contr.,vol.59,no.5,pp.1348−1354,May2014.

[25]C.R.Wang,J.Sheng,and H.B.Ji,“Leader-following consensus of a class of nonlinear multi-agent systems via dynamic output feedback control,”Trans.Inst.Meas.Contr.,vol.37,no.2,pp.154−163,Feb.2015.

[26]W.Wang,J.S.Huang,C.Y.Wen,and H.J.Fan,“Distributed adaptive control for consensus tracking with application to formation control of nonholonomic mobile robots,”Automatica,vol.50,no.4,pp.1254−1263,Apr.2014.

[27]J.M.Peng and X.D.Ye,“Distributed adaptive controller for the output synchronization of networked systems in semi-strict feedback form,”J.Franklin Inst.,vol.351,no.1,pp.412−428,Jan.2014.

[28]M.Krstic,P.V.Kokotovic,and I.Kanellakopoulos,Nonlinear and Adaptive Control Design.New York:John Wiley&Sons,Inc.,1995.

[29]D.Swaroop,J.K.Hedrick,P.P.Yip,and J.C.Gerdes,“Dynamic surface control for a class of nonlinear systems,”IEEE Trans.Automat.Contr.,vol.45,no.10,pp.1893−1899,Oct.2000.

[30]D.Wang and J.Huang,“Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form,”IEEE Trans.Neural Netw.,vol.16,no.1,pp.195−202,Jan.2005.

[31]S.J.Yoo and J.B.Park,“Decentralized adaptive output-feedback control for a class of nonlinear large-scale systems with unknown time-varying delayed interactions,”Inform.Sciences,vol.186,no.1,pp.222−238,Mar.2012.

[32]S.C.Tong,Y.M.Li,G.Feng,and T.S.Li,“Observer-based adaptive fuzzy backstepping dynamic surface control for a class of M IMO nonlinear systems,”IEEE Trans.Syst.Man Cybern.B Cybern.,vol.41,no.4,pp.1124−1135,Aug.2011.

[33]T.S.Li,D.Wang,G.Feng,and S.C.Tong,“ADSC approach to robust adaptive NN tracking control for strict-feedback nonlinear systems,”IEEE Trans.Syst.Man Cybern.B Cybern.,vol.40,no.3,pp.915−927,Jun.2010.

[34]G.Sun,D.Wang,Z.H.Peng,H.Wang,W.Y.Lan,and M.X.Wang,“Robust adaptive neural control of uncertain pure-feedback nonlinear systems,”Int.J.Control,vol.86,no.5,pp.912−922,Apr.2013.

[35]Y.M.Li,S.C.Tong,and T.S.Li,“Adaptive fuzzy output feedback dynamic surface control of interconnected nonlinear pure-feedback systems,”IEEE Trans.Cybern.,vol.45,no.1,pp.138−149,Jan.2015.

[36]Y.Yang,D.Yue,and Y.S.Xue,“Decentralized adaptive neural output feedback control of a class of large-scale time-delay systems with input saturation,”J.Franklin Inst.,vol.352,no.5,pp.2129−2151,May2015.

[37]S.J.Yoo,“Distributed consensus tracking for multiple uncertain nonlinear strict-feedback systems under a directed graph,”IEEE Trans.Neural Netw.Learn.Syst.,vol.24,no.4,pp.666−672,Apr.2013.

[38]W.Wang,D.Wang,Z.H.Peng,and T.S.Li,“Prescribed performance consensus of uncertain nonlinear strict-feedback systems with unknown control directions,”IEEE Trans.Syst.Man Cybern.Syst.,vol.46,no.9,pp.1279−1286,Sep.2016.

[39]Y.Zheng,Y.Zhu,and L.Wang,“Consensus of heterogeneous multiagent systems,”IET Contr.Theory Appl.,vol.5,no.16,pp.1881−1888,Nov.2011.

[40]Y.F.Su and J.Huang,“Cooperative output regulation of linear multiagent systems,”IEEE Trans.Automat.Contr.,vol.57,no.4,pp.1062−1066,Apr.2012.

[41]Z.T.Ding,“Consensus output regulation of a class of heterogeneous nonlinear systems,”IEEE Trans.Automat.Contr.,vol.58,no.10,pp.2648−2653,Oct.2013.

[42]X.X.Yin,D.Yue,and S.L.Hu,“Distributed event-triggered control of discrete-time heterogeneous multi-agent systems,”J.Franklin Inst.,vol.350,no.3,pp.651−669,Apr.2013.

[43]S.B.Li,G.Feng,X.Y.Luo,and X.P.Guan,“Output consensus of heterogeneous linear discrete-time multiagent systems with structural uncertainties,”IEEE Trans.Cybern.,vol.45,no.12,pp.2868−2879,Dec.2015.

[44]X.F.Zhang,L.Liu,and G.Feng,“Leader-follower consensus of time varying nonlinear multi-agent systems,”Automatica,vol.52,pp.8−14,Feb.2015.

[45]Z.H.Qu,Cooperative Control of Dynamical Systems:Applications to Autonomous Vehicles.London:Springer-Verlag,2009.

[46]S.S.Ge,C.C.Hang,T.H.Lee,and T.Zhang,Stable Adaptive Neural Network Control.US:Springer,2002.

[47]C.Wang,D.J.Hill,S.S.Ge,and G.R.Chen,“An ISS-modular approach for adaptive neural control of pure-feedback systems,”Automatica,vol.42,no.5,pp.723−731,May2006.

[48]A.M.Zou,Z.G.Hou,and M.Tan,“Adaptive control of a class of nonlinear pure-feedback systems using fuzzy backstepping approach,”IEEE Trans.Fuzzy Syst.,vol.16,no.4,pp.886−897,Aug.2008.

[49]S.C.Tong,Y.M.Li,and Y.J.Liu,“Adaptive fuzzy output feedback decentralized control of pure-feedback nonlinear large-scale systems,”Int.J.Robust Nonlinear Control,vol.24,no.5,pp.930−954,Mar.2014.

[50]E.Kim and S.Lee,“Output feedback tracking control of MIMO systems using a fuzzy disturbance observer and its application to the speed control of a PM synchronous motor,”IEEE Trans.Fuzzy Syst.,vol.13,no.6,pp.725−741,Dec.2005.

[51]C.Kwan and F.L.Lew is,“Robust backstepping control of nonlinear systems using neural networks,”IEEE Trans.Syst.Man Cybern A Syst.Hum.,vol.30,no.6,pp.753−766,Nov.2000.

[52]W.He,Y.H.Chen,and Z.Yin,“Adaptive neural network control of an uncertain robot with full-state constraints,”IEEE Trans.Cybern.,vol.46,no.3,pp.620−629,Mar.2016.

[53]W.He,S.Zhang,and S.S.Ge,“Adaptive control of a flexible crane system with the boundary output constraint,”IEEE Trans.Ind.Electron.,vol.61,no.8,pp.4126−4133,Aug.2014.

[54]X.M.Zhang,Q.L.Han,and X.H.Yu,“Survey on recent advances in networked control systems,”IEEE Trans.Industr.Inform.,vol.12,no.5,pp.1740−1752,Oct.2016.