The Formation Control of Multi-agent Systems on a Circle

Qiang Wang,Yuzhen Wang,and Huaxiang Zhang

I.INTRODUCTION

MULTI-AGENT systems have attracted a lot of attention of researchers from various areas in the past decades[1]−[7].As an important and fundamental issue in multiagent systems,the formation control problem is an interesting topic in biology,automatic control,robotics,artificial intelligence etc,which requires each agent to move according to the prescribed trajectory.At present,many control strategies have been developed to achieve their control objectives.In general,the main research methods can be generalized as three categories[8],[9],namely,the leader-following approach[10]−[14],the behavior-based approach[15]−[17],and the virtual structure approach[18]−[21].

As a special issue,researchers are interested in the formation control problem based on the prescribed orbit,and there are some literature reports on this issue.In[22],the authors proposed a design methodology to stabilize isolated relative equilibria in a model of all-to-all coupled identical particles moving in a plane at unit speed.A cooperative controlalgorithm was provided to stabilize symmetric formations of motion around closed curves suitable for mobile sensor networks in[23],and a planar particle model with decentralized steering control subject to limited communication was studied in their research.S.Hernandez and D.A.Paley[24]considered the three-dimensional motion coordination in a spatiotemporal flow field,and provided a Lyapunov-based control design to steer a system of self-propelled particles traveling in three dimensions at a constant speed relative to a spatiotemporal flow field.

Motivated by the issues above,we consider the multi-agent system with a cyclic graph topology moving in the plane in this article,and investigate the formation control problem of the multi-agent system on a circle from the following two perspectives:the agents with single-integrator kinematics and the agents with double-integrator kinematics.

The main contributions of this study include the following contents:Firstly,for single-integrator kinematics,two control protocols are designed under which the multi-agent system is able to keep a uniformly-spaced formation based on the method of state-space decomposition[25],[26].Furthermore,the performances of the system under these two protocols are compared in detail.Secondly,for the double-integrator kinematics,we propose a control protocol under which a control protocol is designed for this case.Comparing with the existing results,our studies are based on a class of special topologies,named a cyclic graph,and our control protocols have the explicit physical meanings.Moreover,an analysis method based on complex matrix is presented which avoids trigonometric functions.Finally,three simulations are studied by using our presented results.The study of illustrative examples with simulations shows that our results as well as designed control protocols work very well in studying the formation control of this class of multi-agent systems on a circle.

The rest of the paper is organized as follows.Section II is about the problem formulation and preliminaries.Section III contains the main results of the paper.In this section,some properties on graph theory and hermitian matrix are provided first,and three control protocols are designed.In Section IV,we give three illustrative examples to support our new results followed by the conclusion in Section V.

II.PROBLEM STATEMENT AND PRELIMINARIES

In this section,we give the problem statement first,and then provide some preliminaries on algebraic graphs,which will be used in the sequel.

Consider the system withnagents moving on a circle in two cases,in the first case each agent has single-integrator kinematics described by

and in the other each agent has double-integrator kinematics described by

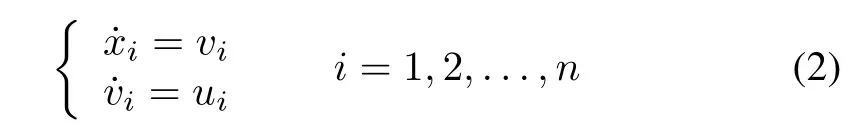
wherexi∈C is the state of agentiand satisfiesC is the velocity of agenti,andui∈C is the control input of agenti,i=1,2,...,n.Sinceris a constant,without loss of generality,we letr=1 in this study.

Remark 1:In this research,assume that the scale of an agent is much less than the radius of the orbit.Thus,an agent can be treated as a particle.

The objective of this paper is to design control protocols such that the system(1)and(2)can retain a stable uniformly spaced formation on a circle.

Case I:Considernagents on a circle,each with singleintegrator kinematics.

Case II:Considernagents on a circle,each with doubleintegrator kinematics.

In the following,we recall some fundamental know ledge on algebraic graph theory and matrix theory,which will be used in the development of this research.

SupposeG={V,E,A}be an undirected graph ofn-th order with the set of nodesV:={v1,v2,...,vn},the set of edges(i.e.,ordered pairs of the agents)andassigning a(positive)weight to each edge such that ifeij:=(vi,vj)∈E,A(eij)=aij.The matrixA=[aij]n×nis named the adjacency matrix of the graphG.For anyi,j∈V,aij＞0 if and only ifj∈N i,whereN i=For notational convenience,we just consider the case of the simple graph in this research,that is,eii/∈E,i=1,2,...,n.The matrixis the valency matrix of the topologyG,anddijis defined as

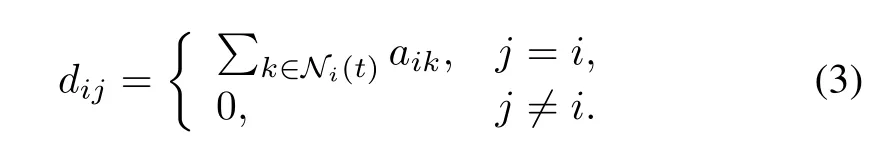
Moreover,the matrixL=D−Ais named the graph’s Laplacian matrix.

Definition 1:Assume that the adjacency matrixAsatisfies

then the matrixAis named a cyclic matrix.

Definition 2:Suppose that the adjacency matrixAis a cyclic matrix,then the corresponding graph is named the cyclic graph(see Fig.1).

It is apparent that the cyclic graph is a connected graph.

Fig.1.A cyclic graph with 5 nodes.

III.MA IN RESULTS

This section studies the uniformly-spaced formation of the multi-agent system(1)and(2)with a cyclic graph topology(see Fig.1),and presents a number of new results for the following two cases:I)each agent with single-integrator kinematics;II)each agent with double-integrator kinematics.

A.The Case of Each Agent With Single-integrator Kinematics

In this subsection,we consider a group ofnagents,each of which has single-integrator kinematics.

Consider the system(1),and assume that its information topology is a cyclic graph,denoted byG.

For this case,we first consider a control protocol as follows:

wherej2=−1.

Substituting(5)into the system(1)yields

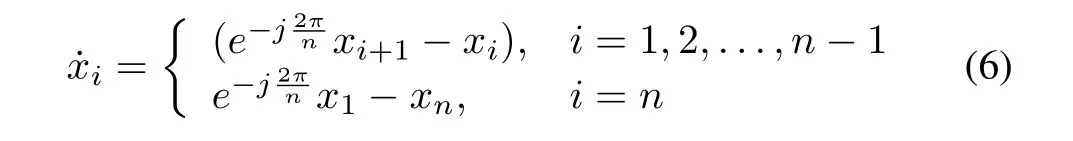
which can be rewritten as

whereandAis expressed as

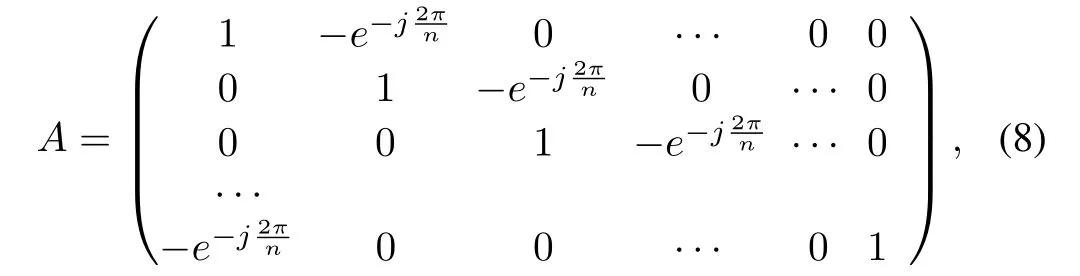
Before we give main results of this part,three lemmas will be presented in the sequel.

Lemma 1:Assume the matrixFis a hermitian matrix,then there exists a unitary matrixU,such thatF=UHΛU,where Λ is a diagonal matrix,and the diagonal elements are real numbers[27].

Letting the matrixG=A+AH,then the other lemma can be expressed as follows:

whereBis a matrix whose eigenvalues have positive realparts but a unique zero,and the eigenvector of zero is denoted asη1,then,x→z0η1,z0is a constant dependant onx0.

Proof:Consider the system(9),sinceBis a matrix whose eigenvalues have positive real parts but a unique zero,then rank(B)=n−1,andRe(B)≥0.

Denotel1,l2,...,lsandη1,η2,...,ηnas the eigenvalues andnlinearly independent generalized eigenvectors of the matrixB,respectively.Without loss of generality,we letl1= 0 andη1be its eigenvector.Construct the matrixT:=[η1,η2,...,ηn],and takez=T−1xas a coordinate transformation.Under the new coordinate transformation,the system(9)can be changed into

wherezzz=[z1,z2,...,zn]T∈Rn,andJis the Jordan canonical form ofB.

Definezzze=[z2,...,zn]T∈Rn−1.Thenzzz=[z1,zzzTe]T,with which the closed-loop dynamics(10)can be rewritten as

whereJe=diag{J2,J3,...,Js}∈R(n−1)×(n−1),Jiis the Jordan canonical block with respect to the eigenvalueli.

Consider the subsystem(12),sincefor alli≥2,it is easy to obtain thatzzze→0.On the other hand,˙z1(t)≡0 implies thatz1(t)≡z1(0).Therefore,zzz(t)→[z1(0),0,...,0]Tast→ ∞.Meanwhile,noticex=Tzand the construction ofT,we have

aswherezzz(0)= [z1(0),z2(0),...,zn(0)]T=T−1x(0),x(0)is the initial condition of the system(9).

Based on the lemmas as above,we will give the following theorem on the multi-agent system(1)under the protocol(5).

Theorem 1:Consider the multi-agent system(1)with a cyclic graph topologyG.Then,the system is stable and all the agents are uniformly-spaced on a circle under the protocol(5).

Proof:Consider the system(7),and choose the Lyapunov candidate functionV(X)=X H X,then we haveSince the matrixGis a hermitian matrix,then there exists a unitary matrixUsuch thatG=UHΛUfrom Lemma 1,where Λ =andλiis the real eigenvalue of matrixG,i=1,2,...,n.

From Theorem 1,the control protocol(5)can ensure the system(1)run on a circle in a uniformly-spaced formation.However,the topology information has not been used sufficiently and the robustness of this protocol is not strong enough,which is sensitive to the topology.Thus,we will consider another control protocol for the system(1)

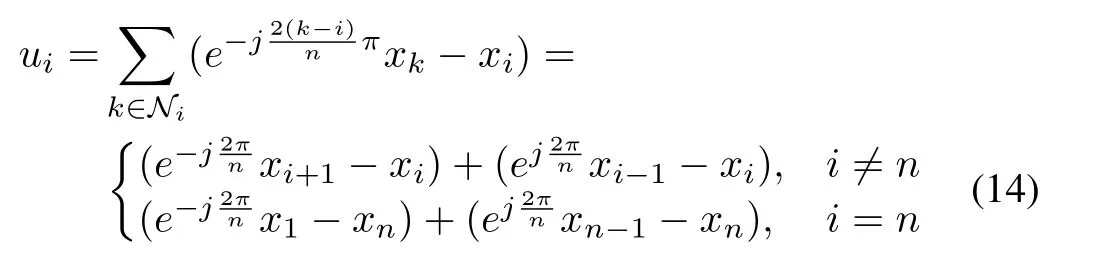
wherej2=−1.

Substituting(14)into the system(1)yields

which can be rewritten as

where,andGis expressed as

it is apparent that the matrixGis a hermitian matrix.

Now,we consider the stability of the system(1)under the control protocol(14),and present another main result of this part.

Theorem 2:Consider the multi-agent system(1)with a cyclic graph topologyG.Then,the system is stable and all the agents are uniformly-spaced on a circle under the protocol(14).

B.The Case of Each Agent With Double-integrator Kinematics

In this part,we consider the case that each agent has doubleintegrator kinematics on a circle.

Consider the system(2),and assume that its information topology is a cyclic graph,denoted byG,and the corresponding adjacency matrix isGas above.In this case,we design a control protocol as follows:

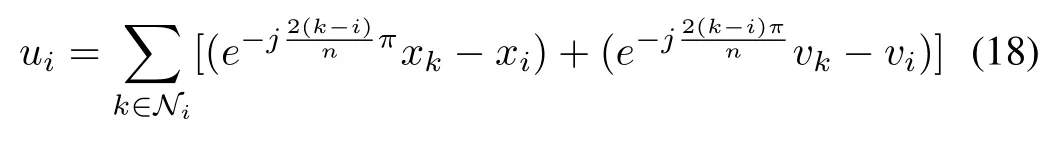
Now substituting(18)into the system(2)yields

Letthen the system(19)can be rewritten as

whereGis expressed as above.

According to the property of matrixG’s eigenvalues,we have the following theorem.

Theorem 3:Consider the multi-agent system(2)with a cyclic graph topologyG.Then,the system is stable and all agents keep a uniformly-spaced formation on a circle under the protocol(18).

Proof:Consider the system(20),denoted asthen we can obtain thatFurthermore,we letandthen denoting

It is apparent that

whenChoose the Lyapunov function candidate

Next,we will give the value ofω0.Let the initial velocitiesand the eigenvectors of the matrixGareη0,η1,...,ηn−1(ηican be obtained by Lemma 2),whereGηi=λiηiandλ0=0.Sinceλi/=λj,i/=j,the eigenvectorsη0,η1,...,ηn−1are linearly independent from Lemma 2.Denoting the matrixQ=[η0,η1,...,ηn−1],it is easy to obtain that the matrixQis nonsingular.Letk1η0+k2η1+...+knηn−1=v0,which implies thatQk=pmbv0,wherek=[k1,k2,...,kn]T,it is easy to obtain thatk=Q−1v0.andk1is what we are interested,ω0.

Thus,we conclude that the multi-agent system(20)will keep a uniformly-spaced formation.

IV.ILLUSTRATIVE EXAMPLES AND SIMULATIONS

In this section,we give three illustrative examples to show how to use our results in this research to design control protocols for the formation on a circle.

Example 1:Consider the following 5-agent system running on a circle:

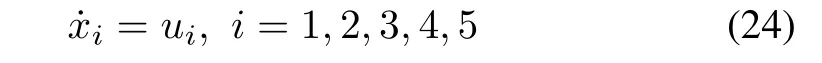
whose topology is shown as Fig.1 and initial conditions are given asin which4,5.

Now,we apply Theorem 1 to design a control protocol for the formation of 5 agents.From Theorem 1,the desired protocol can be designed as

To show the correctness of the above conclusion,we carry out the numerical simulations.The simulation results are shown in Fig.2,which are the curves on the real parts and imaginary parts of state differences with time.

Fig.2.The curves on the real parts and imaginary parts of state differences with time,

It can be seen from Fig.2 that the states of the 5 agents eventually keep a uniformly-spaced formation under the protocol(25)and the final results coincide with the theoretical analysis.Simulations show that our method is very effective in analyzing the formation of this kind of multi-agent system(24).

Example 2:Consider the multi-agent system(24),whose topology is shown as Fig.1 and initial conditions are given as the same as Example 1,in whichx(0)=[x1(0),x2(0),x3(0)and‖xi‖=1

Now,we apply Theorem 2 to design a control protocol for the formation control of 5 agents.The desired protocol is designed as

According to Theorem 2,the multi-agent system(24)can realize a uniformly-spaced formation under the protocol(26).

To show the correctness of the above conclusion,we carry out the numerical simulations with the same initial conditions as Example 1,The simulation results are shown in Fig.3,which are the curves of states.

Fig.3.The curves on the real parts and imaginary parts of state differences with time,

Comparing Fig.2 with Fig.3,it is easy to obtain that the system(24)converges faster under the protocol(26)than the protocol(26)with the same initial conditions.

Example 3:Consider the following 5-agent system moving on a circle:

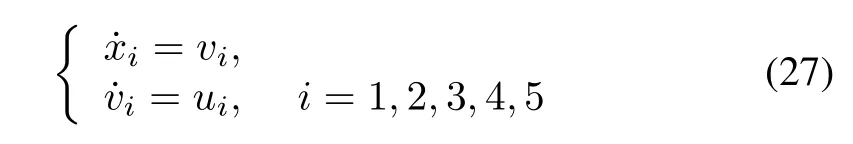
whose topology is shown as Fig.1 and initial conditions are given asandin which

According to Theorem 3,the control protocol could be designed as follows:

To show the correctness of the above conclusion,we carry out the numerical simulations.With the initial conditions above,Fig.4 shows real parts and imaginary parts of the simulation states on the trajectory,and Fig.5 is the results of real parts and imaginary parts of the velocities on the trajectory exp(−j2/5∗π)v(i+1)−v(i),respectively.

Fig.4.The curves of the real parts and the imaginary parts of state differences with time,exp(−j2/5∗π)x(i+1))−x(i).

From Figs.4 and 5,it is clear that the multi-agent system(27)will keep a uniformly-spaced formation under our protocol.

V.CONCLUSION

In this paper,we have investigated the formation control of a class of multi-agent systems moving on a circle,whose topology was a cyclic graph,and several new results were presented for the following two cases:the agents with single-integrator kinematics and the agents with double-integrator kinematics.For the case of single integrator kinematics,two control protocols were proposed under which the multi-agent systems kept a uniformly spaced formation,and the performances about these two protocols were compared in detail.For the case of double-integrator kinematics,a control protocol was designed and the stability of the formation was proved later.Finally,several simulations were studied by using our presented results.The study of illustrative examples with simulations showed that our results worked very well in studying the formation control of this class of multi-agent systems.

Fig.5.The curves of the real parts and the imaginary parts of velocity differences with time,

VI.PROOF OF LEMMA 2

Proof:First we prove the eigenvalues of matrix

are,k=0,1,2,...,n−1.

Let the determinant

[1]B.Xu,J.L.Bai,Y.L.Hao,W.Gao,and Y.L.Liu,“The research status and progress of cooperative navigation for multiple AUVs,”Acta Automat.Sin.,vol.41,no.3,pp.445−461,Mar.2015.

[2]W.Ni and D.Z.Cheng,“Leader-following consensus of multi-agent systems under fixed and switching topologies,”Syst.Control Lett.,vol.59,no.3−4,pp.209−217,Mar.CApr.2010.

[3]T.Liand J.F.Zhang,“Asymptotically optimal decentralized control for large population stochastic multiagent systems,”IEEE Trans.Automat.Control,vol.53,no.7,pp.1643−1660,Sep.2008.

[4]Y.Z.Wang,C.H.Zhang,and Z.B.Liu,“A matrix approach to graph maximum stable set and coloring problems with application to multiagent systems,”Automatica,vol.48,no.7,pp.1227−1236,Jul.2012.

[5]Y.Zhang and Y.P.Tian,“Consent ability and protocol design of multiagent systems with stochastic switching topology,”Automatica,vol.45,no.5,pp.1195−1201,May 2009.

[6]Q.Wang and Y.Z.Wang,“Cluster synchronization of a class of multiagent systems with a bipartite graph topology,”Sci.China Inform.Sci.,vol.57,no.1,pp.1−11,Jan.2014.

[7]Z.X.Wang,D.J.Du,and M.R.Fei,“Average consensus in directed networks of multi-agents with uncertain time-varying delays,”Acta Automat.Sin.,vol.40,no.11,pp.2602-2608,Nov.2014.

[8]F.Xiao,L.Wang,J.Chen,and Y.P.Gao,“Finite-time formation control formult-agent systems,”Automatica,vol.45,no.11,pp.2605−2611,Nov.2009.

[9]X.K.Wang,X.Li,and Z.Q.Zheng,“Survey of developments on multiagent formation control related problems,”Control Dec.,vol.28,no.11,pp.1601−1613,Nov.2013.

[10]H.S.Su,M.Z.Q.Chen,X.F.Wang,and J.Lam,“Semiglobal observerbased leader-following consensus with input saturation,”IEEE Trans.Industr.Electron.,vol.61,no.6,pp.2842−2850,Aug.2014.

[11]H.S.Su,M.Z.Q.Chen,J.Lam,and Z.L.Lin,“Sem i-global leader following consensus of linear multi-agent systems with input saturation via low gain feedback,”IEEE Trans.Circ.Syst.I,vol.60,no.7,pp.1881−1889,Mar.2013.

[12]J.Chen,D.Sun,J.Yang,and H.Y.Chen,“Leader-follower formation control of multiple non-holonomic mobile robots incorporating a receding-horizon scheme,”Int.J.Robot.Res.,vol.29,no.6,pp.727−747,May 2010.

[13]B.Liu,T.G.Chu,L.Wang,and G.M.Xie,“Controllability of a leader-follower dynamic network with switching topology,”IEEE Trans.Automat.Control,vol.53,no.4,pp.1009−1013,May 2008.

[14]D.V.Dimarogonas,P.Tsiotras,and K.J.Kyriakopoulos,“Leader follower cooperative attitude control of multiple rigid bodies,”Syst.Control Lett.,vol.58,no.6,pp.429−435,Jun.2009.

[15]C.W.Reynolds,“Flocks,herds and schools:A distributed behavioral model,”ACM SIGGRAPH Comp.Graph.,vol.21,no.4,pp.25−34,Jul.1987.

[16]A.Jadbabaie,J.Lin,and A.S.Morse,“Coordination of groups of mobile autonomous agents using nearest neighbor rules,”IEEE Trans.Automat.Control,vol.48,no.6,pp.988−1001,Jun.2003.

[17]G.Antonelli,F.Arrichiello,and S.Chiaverini,“Experiments of formation control with multirobot systems using the nullspace-based behavioral control,”IEEE Trans.Control Syst.Technol.,vol.17,no.5,pp.1173−1182,Apr.2009.

[18]H.S.Su,X.F.Wang,and Z.L.Lin,“Flocking of multi-agents with a virtual leader,”IEEE Trans.Automat.Control,vol.54,no.2,pp.293−307,Feb.2009.

[19]M.A.Lew isand K.H.Tan,“High precision formation control of mobile robots using virtual structures,”Autonom.Robots,vol.4,no.4,pp.387−403,Oct.1997.

[20]W.Ren and R.Beard,“Decentralized scheme for spacecraft formation flying via the virtual structure approach,”J.Guid.Control Dynam.,vol.27,no.1,pp.73−82,Jan.-Feb.2004.

[21]R.W.Beard,J.Law ton,and F.Y.Hadaegh,“A coordination architecture for spacecraft formation control,”IEEE Trans.Control Syst.Technol.,vol.9,no.6,pp.777−790,Nov.2001.

[22]R.Sepulchre,D.A.Paley,and N.E.Leonard,“Stabilization of planar collective motion:A ll-to-all communication,”IEEE Trans.Automat.Control,vol.52,no.5,pp.811−824,May 2007.

[23]D.A.Paley,N.E.Leonard,and R.Sepulchre,“Stabilization of symmetric formations to motion around convex loops,”Syst.Control Lett.,vol.57,no.3,pp.209−215,Mar.2008.

[24]S.Hernandez and D.A.Paley,“Three-dimensional motion coordination in a spatiotemporal flow field,”IEEE Trans.Automat.Control,vol.55,no.12,pp.2805−2810,Sep.2010.

[25]Q.Wang,Y.Z.Wang,and R.M.Yang,“Design and analysis of group consensus protocol for a class of multi-agent systems,”Control Dec.,vol.28,no.3,pp.369−373,Mar.2013.

[26]Q.Wang and Y.Z.Wang,“Cluster synchronization of a class of multiagent systems with a bipartite graph topology,”Sci.China Info.Sci.,vol.57,no.1,pp.1−11,Jan.2014.

[27]B.R.Fang,J.D.Zhou,and Y.M.Li,Matrix Theory.Beijing:Tsinghua University Press,pp.116,2013.