Collision-free Scheduling of Multi-bridge Machining Systems:A Colored Traveling Salesman Problem-based Approach

Jun Li,Xianghu Meng,and Xing Dai

I.INTRODUCTION

MULTI-BRIDGE machining systems(MBMS)as important processing equipment for production have been paid great attention by both academia and industry.Such a system contains at least two concurrent individual bridge machines and an over lapping work space shared by them.Each machine is required not only to perform the tasks in its own section of workspace but also to complete together with others the tasks in the overlapping section shared by them.Meanwhile,they are subject to some process and geometric

Such systems face three common problems at the operational level,i.e.,job partition/assignment,job scheduling and collision resolution or machine coordination.A job scheduling problem is to determine the best job sequence for each individual machine after job partition and assignment.Collision resolution is to implement orderly execution of jobs assigned to multiple machines while avoiding their collision.Solving them is crucial for promoting the production efficiency and enhancing the reliability of the systems.constraints,e.g.,collision avoidance.Two MBMS are cited as typical examples,i.e.,a dual-bridge waterjet machining center and a dual-manipulator hull welding system,as illustrated in Fig.1.Both consist of two independent individual machines,i.e.,cutting machines and manipulators.The overlap between two individual workspaces is required in order to guarantee no dead processing zone.Either but only one of two neighboring machines is allowed to perform any shared jobs in their overlapping zone.

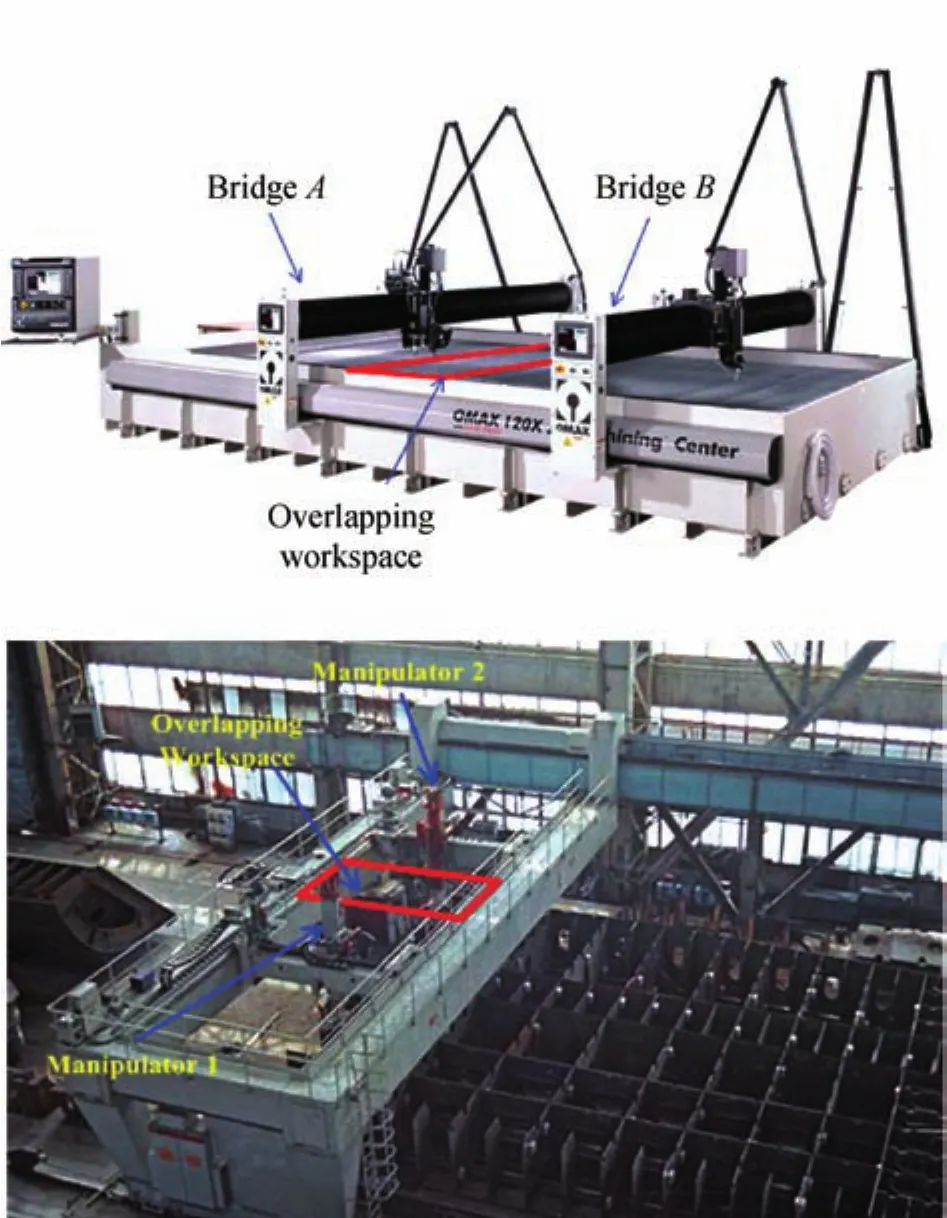
Fig.1.Two MBMS.(a)Dual-bridge waterjet cutting machine tool,and(b)Gantry dual-manipulator hull welding system.

Our prior work[1],[2 has presented a genetic algorithm for collision-free path planning of three-bridge waterjet cutting.Menget al.,[3]examine a cutting task sequencing method for dual-bridge waterjet cutting with collision avoidance via population-based incremental learning(PBIL).A ll achieve a collision-free schedule by searching first and then increasing time intervals among jobs to resolve potential collisions between two neighboring bridges once the search fails.Our prior work[4]−[7]proposes a colored traveling salesman problem(CTSP)in which each salesman has an exclusive city set of the same color and all salesmen share only one common city set of multiple colors.Here,we rename it a radial-CTSP(R-CTSP)to differentiate it from the one to be proposed.It has been applied to the path planning of a dual-bridge waterjet cutting machine tool[8].It is applicable to multiple machine systems containing radially arranged individual machines whose workspaces have a single common section.The scheduling of an MBMS with two machines can be formulated as a specific case of R-CTSP with two salesmen.However,R-CTSP cannot be applied to MBMS with multiple machines sharing multiple common sections.

This work proposes a serial-CTSP(S-CTSP)to abstract the scheduling problems of MBMS.Based on it and its solution algorithm,we develop an integrated method for resolving both job scheduling and coordination problems of MBMS.The main contributions are to:

1)Propose an S-CTSP in which each salesman has some exclusive cities and shares some cities with its neighbor(s).It differs from R-CTSP but they are identical when both have only two salesmen.A greedy algorithm is developed for solving S-CTSP.It assigns a shared city in a random manner during stepwise neighboring city search satisfying proximity.

2)Develop a collision-free scheduling method to perform both job scheduling and collision resolution of MBMS.It is an augmented greedy algorithm that introduces some timing constraints for a collision-free job selection together with a collision resolution mechanism which is only used when such a selection fails.

3)Apply S-CTSP and the proposed methods to a triple bridge waterjet cutting process of a large world map.The cutting job assignment,basic path scheduling,and collision free path scheduling are demonstrated.

The rest of the paper is organized as follows.Section II reviews the related work.S-CTSP and its algorithm are proposed in Section III.Section IV gives the collision-free scheduling method.A case study of a three-bridge waterjet cutting process is presented in Section V.Section VI concludes this paper.

II.RELATED WORK

In some multiple machine systems,machines are required to perform all jobs and a job can be executed exactly once by a machine.After all jobs are accomplished all machines return to their depots.It seems that the job scheduling problem of such a system can be attributed to a multiple traveling salesman problem(MTSP)[9]or transformed into a traveling salesman problem(TSP)[10].Namely,jobs,machines,and the objective of job scheduling can be represented as cities,salesmen,and an objective function of MTSP or TSP,respectively.For example,the motion of multiple robots is planned to cover a point set as multiple single TSP[11];the job scheduling of a dual-manipulator manufacturing cell is modelled as an MTSP[12];and the test ordering problem of a new equipment with four mobile probes for testing printed circuit boards is formulated as a TSP[13].The authors have made some changes to the original problems for convenience of solutions.Either of the similarity or difference of tasks is thus neglected.Note that some tasks in MBMS are exclusive for specified machines and some allow any one of neighboring machines to perform.Both MTSP and multiple individual TSPs cannot represent simultaneously such different and identical groups of tasks since their cities are either identical or different from each other in term of their accessibility by salesmen.Formulating the scheduling problems as MTSP or TSP may change their original solution space.Our prior work[4]−[7]presents an R-CTSP by differently coloring cities to catch the features of the scheduling problems.The differences among R-CTSP,MTSP and multiple single TSPs are disclosed in[4],[7].It confirms that CTSP has a much larger solution space than the combination of multiple individual TSPs but smaller than MTSPwith respect to the same problem size and coding scheme.Then,we apply R-CTSP to the path planning of a dual-bridge waterjet cutting machine tool[8].

There are many approaches to both the scheduling and coordination problems of multi machine systems not limited to MBMS.Motion planning and collaboration of robots are often addressed together in multi-robot collaboration systems[14],[15].A scheduling method for deadlock avoidance of a robotized manufacturing cell is reported in[16].As mentioned,Chakrabortyet al.[11]plan collision-free motions of multiple robots in an electronics manufacturing system to cover a point set as TSPs subject to geometric constraints,and Xidiaset al.[12]develop a genetic algorithm(GA)coding with an inverse kinematics solution for collision-free scheduling of a dual manipulator manufacturing cell.Gonzalez-Rodriguezet al.[13]examine new equipment with four mobile probes for testing printed circuit boards.They solve the test ordering problem for multiple probes as a TSP first and then implement their motion coordination.Other approaches to task allocation and interaction of multiple robots are reported by Dahlet al.[17],Korsahet al.[18],and Zhenget al.[19].Our prior works propose a motion control method for collaborative welding of multiple manipulators under the circumstance without fixtures[20],and a collision-free path planning method based on a genetic algorithm for three-bridge waterjet cutting[1],[2]and one based on PBIL for dual-bridge waterjet cutting[3].Liet al.[2]and Du[1]insert waiting time to the obtained schedule to avoid two neighboring bridges co-locating in the same overlapping processing zone to resolve their collision.Menget al.[3]give a method to derive a collision-free schedule.These methods have to be generalized in order to make their application wider.

III.S-CTSP AND GREEDY ALGORITHM

A.S-CTSP Formulation

Our prior work[4]−[7]propose a basic CTSP,radial-CTSP.This paper focuses on a new class of CTSP,i.e.,serial CTSP withmsalesmen andncities,wherem＜nandn,m∈Z={1,2,3,...}.It is defined over a complete digraphG=(ℵ,E),where vertex setℵ={1,2,...,n}numbers the cities;and each edge(i,j)∈E,i/=j,is associated with a weightωijrepresenting a visit cost(e.g.,distance)between two citiesiandj.ℵis divided into 2m−1 disjoint non-empty sets,i.e.,exclusive city setsVi,∀i∈Zm={1,2,...,m},and shared city setsUj,∀j∈Zm−1.A salesmaniis assigned with colori.∀a∈Vi,its colorican be only be visited by salesmani.∀a∈Uj,ρ(a)={j,j+1}meaning both salesmeniandjcan visita.For example,salesmen 1−3 visit,andU2∪V3,in Fig.2,respectively.Vertexdi∈Virepresents the depot where salesmanideparts and returns.The objective of S-CTSP is to determinemHamiltonian cycles overGwith the least total tour cost.

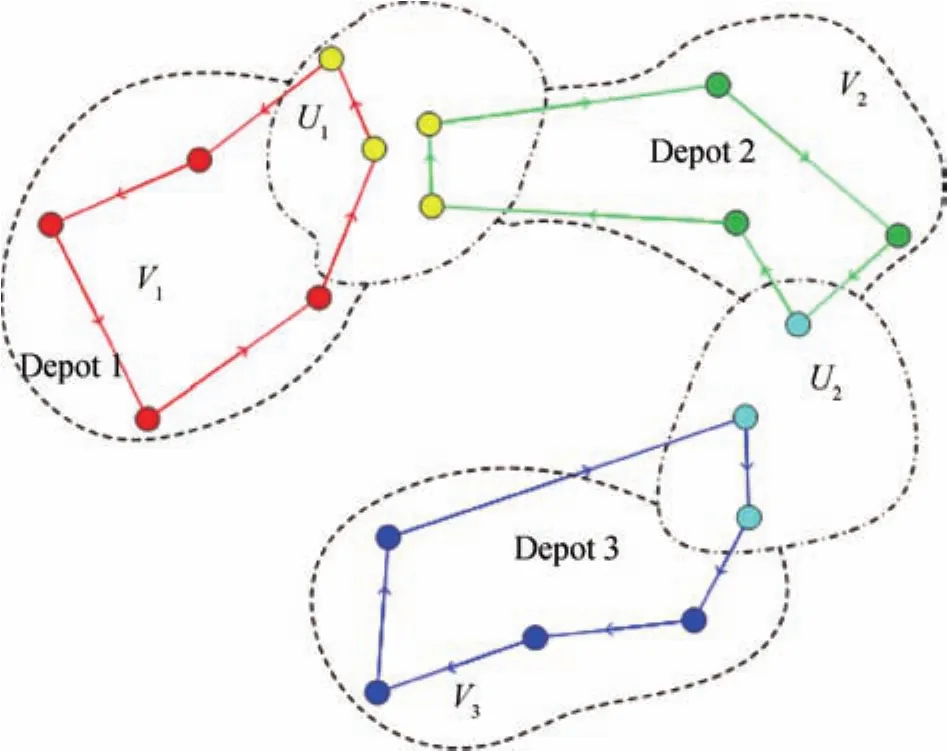
Fig.2.Example of S-CTSP with 3 salesmen sharing 2 common city sets.

Next,S-CTSP is formulated as a 0-1 integer programming model.LetU0=Um=Vm+1=Øfor mathematical convenience.The accessible city set of salesmankisℵk=.Binary access variablesxijk=1,i/=j,∀i,j∈ℵ,if salesmankpasses through edge(i,j);otherwise,xijk=0.uikis the number of nodes visited on the tour of salesmankfromdkto nodei.

Subject to:Each salesmankis required to start from and return to depotdk:

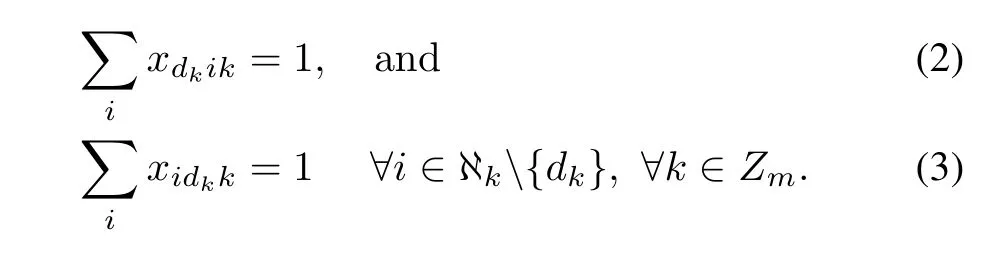
Salesmankcan neither travel to nor from a city outsideℵk:

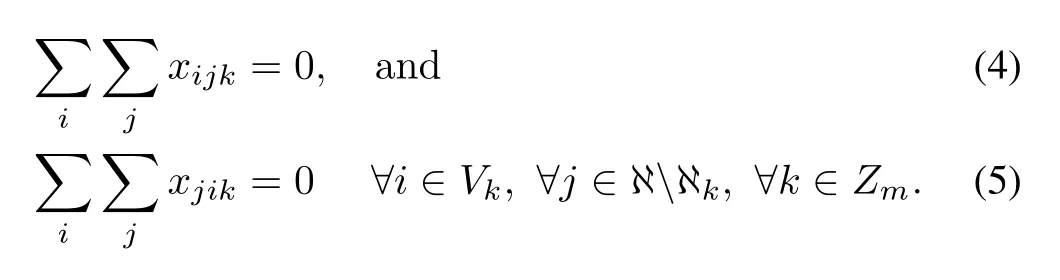
Another salesmanlis forbidden to travel to or from an exclusive city of salesmank:

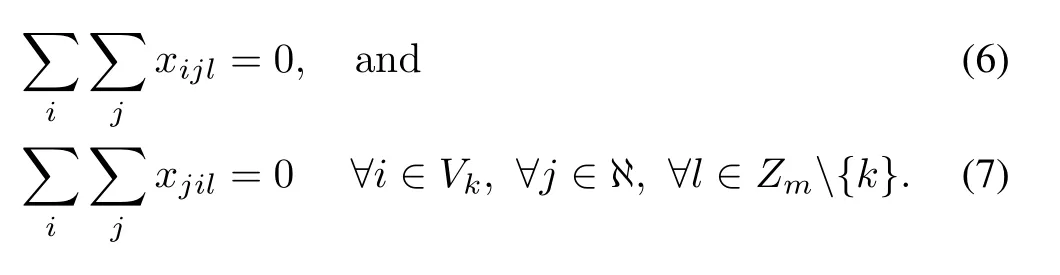
Salesmankcannot visit a city outside its accessible city set from or back to its shared cities:

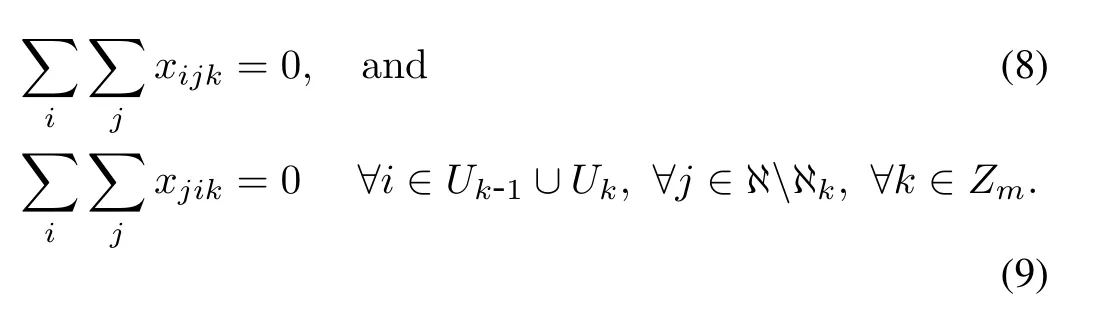
A salesman other than salesmenkandk+1 is forbidden to visit the cities inUkshared by salesmenkandk+1:

Each city can be visited by one salesman exactly once:

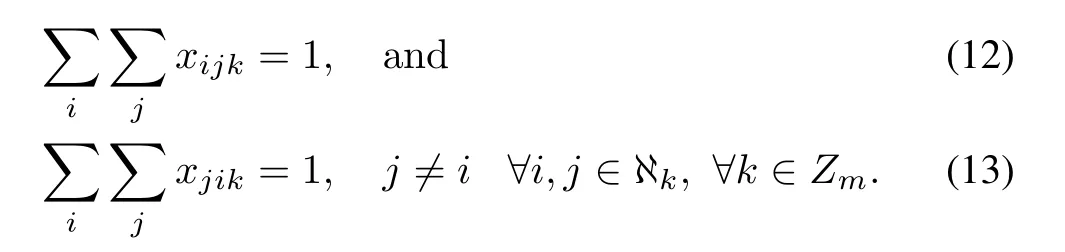
A shared city cannot be disconnected from a tour once it is visited by a salesman:

Any solution consisting of several disconnected sub-tours for a salesman must be forbidden,as indicated by the following equation incorporated with(14):

S-CTSP is new and was never formulated before to the best know ledge of the authors.S-CTSP and R-CTSP become identical when they have only two salesmen.R-CTSP is proven to be NP-hard[6].So is S-CTSP.

B.Greedy Algorithm for S-CTSP

We cannot solve exactly S-CTSP with city size 40 via LINGO within two days.A greedy algorithm is an algorithm that follows the problem solving heuristic of making the locally optimal choice at each stage with the hope of finding a global optimum[21].In many problems,a greedy strategy may not produce a global optimal solution but a local one that approximates the global one in a reasonable time.This algorithm has been applied to TSP and can quickly yield an effectively short route[22].We develop it to solve S-CTSP.To grasp the characteristics of S-CTSP,we allow the algorithm to assign a shared city to a salesman in a random manner during stepwise neighboring city search satisfying proximity.It contributes to the greater solution space and more chances to achieve the best solution than the original greedy algorithm does.Note that the assignment of shared cities is fixed and thus only one solution exists in the original greedy algorithm.

Suppose that the solution of an S-CTSP is denoted asX=(X1,X2,...,Xm),whereX irepresents the route of salesmani,∀i∈Zm.The depot of a salesman is only regarded as the head of the corresponding route sequence and is taken into account as the home to close the route so as to satisfy(2)and(3).A ll the following symbols are the same as those mentioned in Section III.We letqk=|Uk|,rk=|Vk|,andnk=|ℵk|,∀k∈Zm.

Each salesman in an S-CTSP needs to not only traverse all its exclusive cities but also visit randomly some shared cities.The city visit needs to meet proximity stepwise.Proximity represents a criterion of the least visit cost not limited to the shortest visit distance.A salesman at the current city selects the next unvisited one that is closest to it.It is different for a salesman to select an exclusive city and a shared city.Particularly,given candidate cityaunvisited from accessible city setℵk,ifa/∈Uk,it must belong toVkand should be added to the route of salesmank;otherwise,the Roulette method with a fixed probability is used to determine ifashould be added into the route of salesmankor assigned to salesmank+1 for later selecting.This route search process generates in turn a path for each salesman,starting from and returning to its depot.

Algorithm 1:_Greedy algorithm for S-CT__S_P

7.if a/∈Uk then 8. Add a into X k 9. else assign a to salesman k or k+1 by Roulettewith r 10. if a assigned to salesman k then 11. Add a into X k 12. end if 13. end if 14. ℵk:=ℵk{a}15. until more than nk citieswere searched 16. k:=k+1 17.until k＞m 18.until maximum of running ismet__19.Output:the best solution X=(X1,X2,...,Xm)

IV.S-CTSP-BASED COLLISION-FREE SCHEDULING OF MBMS

A.Job Assignment,Scheduling,and Collision Avoidance Problems

The multi-bridge machining systems investigated herein have multiple bridge machines.A bridge moves along a long system rail and the machine on it performs tasks in a planar or spatial workspace that partially overlaps with its neighbor in series.For example,a waterjet cutting center and welding system have planar and spatial workspaces,as shown in Fig.1,respectively.

As shown in Fig.3,an MBMS hasmindividual bridge machines numbered from 1 tom.The entire system workspace can be divided intomnon-overlapping workspaces andm−1 overlapping workspaces,denoted asW iand,∀i∈Zm={1,2,...,m}and∀j∈Zm−1.Machine 1 has an accessible workspace consisting ofW1and,and machinem,WmandThe accessible workspace of machinei∈Zm{1,m}consists of¯Wi−1,W i,and¯Wi.

Fig.3.Topview of workspace partition of an MBMS.

Three problems arising from MBMS are job assignment,job scheduling,and collision resolution problems.Jobs are continuous line segments,curves,or shapes for machining.They usually distribute over different workspaces and even some cross multiple workspaces.First,these jobs should be partitioned and assigned to specific machines.Usually,there are many jobs in a large workspace in such systems.It is significant to find the best job sequences for multiple machines so as to improve processing efficiency and reduce energy consumption.It is basically a job scheduling problem.In addition,due to an overlapping processing region in such systems,two neighboring machines may collide when both colocate in it to perform their respective tasks.Hence,one has to resolve this collision problem to ensure the system reliability.

The numbered lines and curves,either planar or spatial such as cutting curves and weld seams,are the tasks to be performed.Note that a basic principle to be followed by during task assignment is that,i.e.,a task should be processed continuously by one machine as far as possible. Thus, we have the below policies of task partition and assignment:

a)A curve fully in a machine’s accessible workspace and partially in its non-overlapping workspace must be assigned to it;

b)A task totally in a shared workspace can be assigned at random to either neighboring machines;and

c)A curve crossing over a shared workspace should be partitioned first by the central line of the workspace and then the segments are assigned to the particular machines according to a).

For example,the line segment with endpoints 1 and 2 and ellipse 3 meeting a),should be assigned to machine 1.Rectangle 6 totally in a shared workspace can be assigned to either neighboring machines.Following c),the long rectangle crossing over shared workspace 1 is partitioned into two no noverlapping segments,i.e.,the left for machine 1 and the right for machine 2.

We call an assigned task or task segment a job.The jobs can be classified into several different types,namely,exclusive jobs for each machine and shared jobs for two neighboring machines.We note that the grouping of jobs is not in line with the partition of workspaces.For example,an exclusive job of a machine,e.g.,job 3,meeting a)is not necessarily a complete one in its non-overlapping workspace or partially appears in its overlapping workspace,while a shared job of a machine,e.g.,job 6,must fall entirely in one of its overlapping workspaces.

Each task can be abstracted as one or two dots with a processing duration.In particular,a closed curve will be abstracted to its most left point,e.g.,3 and 6;otherwise,it is abstracted into the two end points,e.g.,1 and 2.Such two endpoints cannot be separately accessed and the corresponding job’s duration will be set as an attribute to the starting point,e.g.,if point 1 is selected as a starting point,the processing duration of the line segment will be assigned to it and the endpoint of processing must be 2,accordingly.

B.Augmented Greedy Algorithm for Collision-free Scheduling

Job scheduling of MBMS can be modeled by an S-CTSP.The assigned jobs and individual machines are modeled as cities and salesmen in an S-CTSP,respectively.Namely,each group of exclusive(shared)jobs is represented as a set of exclusive(shared)cities.The objective of scheduling is to search a job sequence for each machine such that the total job visiting cost of all machines is the least.It can be formulated by the objective function of the corresponding S-CTSP with a specific definition of visit cost.Therefore,Algorithm 1 for S-CTSP is also for basic job scheduling of MBMS.

Collision resolution of any two neighboring bridges can be solved together by such a scheduling.A collision between two bridges must mean that their execution durations have an overlap in their workspaces.Therefore,it can be resolved by eliminating such overlaps when scheduling.Specifically,a solution can try its best to search a job sequence for a machine without such overlaps with its neighboring machine;and remove such an overlap only when it is inevitable in search.

We define theith time window of bridgekas the execution duration defined from its entering time to its exiting time its overlapping workspacek′,denoted as[sk′,i,ek′,i].Given a routeXk,the time window sequence of bridgek,Tk,k′is a sequence,[sk′,1,ek′,1],[sk′,2,ek′,2],...,and[sk′,l,ek′,l],wherelis the times of bridgekentering overlapping workspacek′,k′=kandk′/=m,∀k∈Zm,Before adding a current job into the present job sequence of the current machine,it is necessary to adjust if the job has any time overlaps with those of the previous bridge if it exists,in the corresponding overlapping workspace.When its job sequence is in searching,its time window sequence is unavailable.Therefore,it needs to define a job’s nominal time window(NTW)to represent the period from when a bridge enters an overlapping workspace from the outside to execute the job to when it exits this workspace.NTW is an extension to the job processing period.It makes it possible to estimate potential time overlaps between the current bridge and its previous neighbor.

Fig.4.Time window overlaps between two bridges in their overlapping workspace and their resolution.[sk′−1,i,ek′−1,i]and[sk,j,ek,j]represent time windows of bridge and nominal time window of bridge k’s job j,respectively.τis the delay required for overlap resolution.

Fig.5.Layout of triple-bridge waterjet cutting and a world map to be cut.

During search for a job sequence of the current machine,two cases of overlap resolution should be taken into account,as shown in Fig.4,if such a time overlap cannot be avoided by reselecting another job.First,the overlap between the NTW of a to-be-executed jobjby bridgekand one of the execution time windows of bridgek−1 in their overlapping workspace can be removed,once the former is shifted by a time span.Second,if a new overlap is brought by such a shift,it needs one more shift until no overlaps exist.Thus,solving both problems of an MBMS together can be realized by repeating the above process for bridges one by one.

We augment the greedy algorithm to deal with it as given in Algorithm 2.It takesO(2N N2)time in the worst case as same as Algorithm 1.Step 12 represents that bridgekcannot enter region¯Wk′−1until its neighbork−1 leaves the region so as to resolve the potential conflicts between them.As mentioned in Section II,some exclusive jobs may fall partially in the overlapping workspace besides the shared jobs.Therefore,it is necessary to analyze and deal with the emerging time window overlaps for an exclusive job once itappears in an overlapping workspace.

V.CASE STUDY OF MULTI-BRIDGE WATERJET CUTTING

At present,triple-bridge water cutting is under development.There are neither algorithms nor related CAM software,released for triple-bridge water cutting,to the best know ledge of the authors.In this section we apply the proposed greedy algorithms for S-CTSP and collision-free scheduling to a triple-bridge waterjet cutting application.Fig.5 illustrates the sketch of the center and a world map to be cut by it.Its maximum cutting size is 12m×6m,where the maximum travel of bridges 1−3 is 5m,6m,and 5m,respectively.The three non-overlapping workspaces and two overlapping ones have been marked out.In the map,all separated land shapes are numbered and to be cut from 16marble base plates of size 3m×1.5m×2 cm.The resultant cavities will be filled in with marble blocks of the same shapes but different colors so as to form a mosaic artwork for wall decoration.The traveling and cutting speeds of the machine tool are 10m/min and 40cm/min,respectively.

Algorithm 2: Augmented greedy algorithm for collision-free scheduling of MBMS_____________________________________

A.Cutting Path Planning Considering No Collisions

The land shapes to be cut are numbered from 1 to 64 and the black spots represent the starting or ending spots.Jobs are assigned,in accordance with the policies given in Section II,as follows:jobs 1−12 and 23 as the exclusive ones for bridge 1,jobs 24−33 for bridge 2,and jobs 38−61 for bridge 3.The close outline of the Eurasian and African continent is partitioned by the central line of the first overlapping workspace into two unclosed curves that are assigned to bridges 2 and 3,i.e.,the left curve with two endpoints 54 and 62,respectively.Jobs 13−22 in overlapping region 1 are shared by bridges 1 and 2 and jobs 34−37 in overlapping region 2 are shared by bridges2 and 3.Points65−67 represent the depots of bridges 1−3,respectively.

The optimization objective is to search a route for each head such that the total tour length of all heads is the shortest.The cutting path planning problem of the tri-bridge system can be modeled as an S-CTSP withm=3 andn=67.Namely,the three bridges are modeled as traveling salesmen,three collections of exclusive jobs as three sets of exclusive cities and the two sets of shared jobs as two sets of shared cities.Note that,it is necessary to sequence continuously both endpoints 54 and 62 of the left unclosed curve and endpoints 63 and 64 of the right unclosed curve when planning the cutting paths to represent that the two curves should be cut fully.

Algorithm 1 is used to solve the S-CTSP.The accessible city counts of the three salesmen aren1=23,n2=27,andn3=30;and shared city counts areq1=10 andq2=4.The maximum number of iterations is 214=16384.The probability of city selectionris set to 0.7.The algorithms are implemented in C#language with Microsoft Visual Studio 2012 and runs on Dell Optiplex 390 installed with Windows 7 with CPU Intel Core i3-2130 at 3.40GHz and 4GB RAM.After discarding the duplicate solutions,the total tour length(L)of 10000 different intermediate ones generated by Algorithm I is plotted in Fig.6,whereLis the distance sum between two shape endpoints,i.e.,the total distance of rapid travel.The obtained minimalL,denoted byL∗,is487563mm and meanLdenoted by¯L,52850.5mm.The total computing time spent is about 3.0 seconds.Taking arbitrarily 10 fixed assignments of the shared cities,we perform accordingly the basic greedy algorithm without randomized modification 10 times and obtain the worse results than Algorithm I does,i.e.,biggerL∗=50941.2mm and¯L=54357.1mm,as shown in Fig.7.The mean computing time is 0.0014 seconds.Predeter mined assignment of shared cities transforms S-CTSP into multiple individual TSP.The results indicate that S-CTSP has greater solution space than multiple individual TSP with the same problem size.

B.Collision-free Cutting Path Planning

We apply the augmented greedy heuristics to solve collision free cutting paths for the three bridges and the algorithm parameters remain as before.Its obtained results are listed in Table I.L∗is 50045.6mm when the maximum of concurrent processing time(MCPT)spent by the bridges is1338minutes,including travel and cutting time.A resolution of time window overlap has to be performed,thereby resulting in a delay of 18 minutes.The basic greedy algorithm with collision resolution is also applied to solve collision-free paths for the purpose of comparison.The ten assignments of shared cities above are adopted.It shows that the obtained best and mean results are worse than those of Algorithm 2 with respect toL∗,MCPT,and collision resolution delays(CRD)as listed in Table I.The total computing time spent by Algorithm 2 and the basic greedy algorithm with collision resolution are 3.5 and 0.015 seconds,respectively.We also note that collision-free path schedules are achieved at the cost of route length and processing delays.

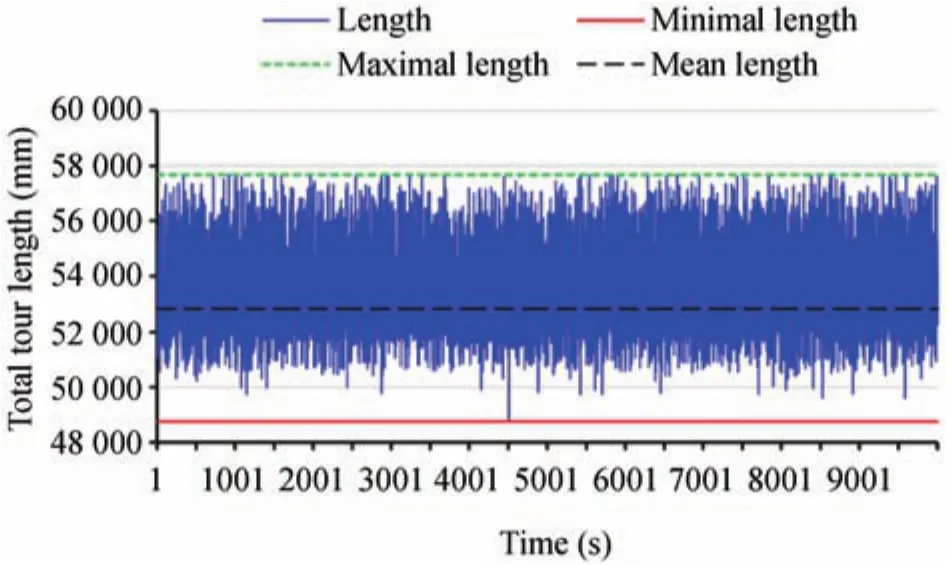
Fig.6.Total route length of 10000 different intermediate results obtained by Algorithm 1.

Fig.7. Total route length of 10 cases with predetermined shared city assignment by the basic greedy algorithm.

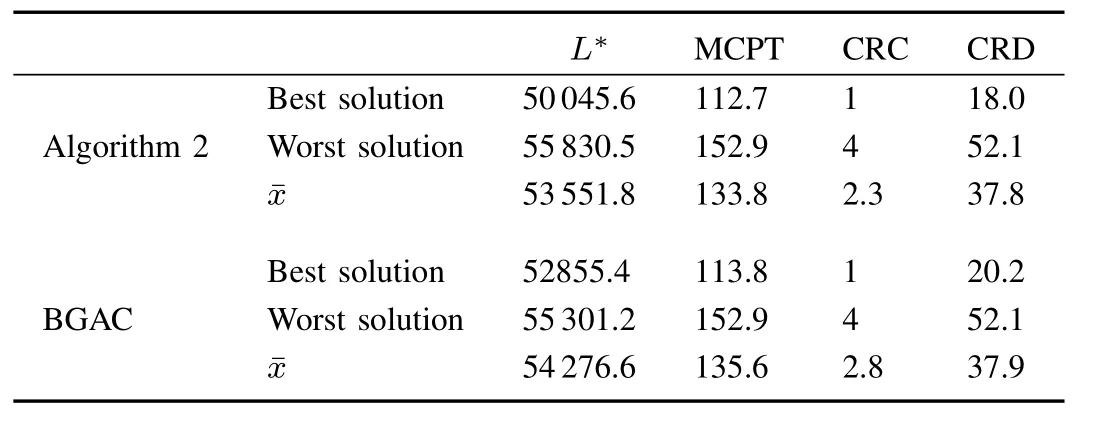
TABLE I RESULTS COMPARISON OF COLLISION-FREE PATH PLANN ING(UNITS:MM AND M IN)

We exploit the plug-in component for multi-bridge waterjet cutting simulation under the platform of AutoCAD to validate the above twenty solutions.It is built with the Object ARX programming environment by our group(Du,2011)and can simulate the travel and cutting processes of three workheads.The results show that no cases of two bridges both exist in the same overlapping processing region at the same time.It indicates that the potential collisions of bridges are avoided by all solutions in Table I.Also,with respect to the solutions with collision resolution,a bridge has to wait to enter an overlapping zone before its neighbor exits from it.In addition,we also note that a change in the timing and sequencing of a solution,e.g.,a change in the sequence of jobs or insertion of waiting,may incur new collisions of bridges.Such a change represents a fault.Usually,all bridges have to halt and resume their execution after the fault treatment.

V I.CONCLUSIONS

This work investigates the job scheduling and coordination problems commonly faced by multi-bridge machining systems.First,a serial colored traveling salesman problem and its greedy algorithm are proposed.The basic scheduling problems of MBMS can be modeled by S-CTSP and solved via our algorithms after the job partition and assignment following some process requirements.An integrated method is developed to solve simultaneously the job scheduling and coordination problems of MBMS.It is implemented by integrating timing constraints into the greedy algorithm to avoid collisions between any two neighboring bridges.Finally,we apply both to a triple-bridge waterjet cutting process and compare their performance.Our ongoing work is to develop new heuristics and evolutionary algorithms.In addition,to achieve fault tolerance ability for MBMS,we also intend to investigate dynamic multi-machine coordination solutions and combine them with S-CTSP-based scheduling.These methods will be applied to the challenging manipulation problem of large-size 3D printing.

[1]Z.Du,“A coordination and optimization method for cutting processes of multi-bridge waterjet systems,”M.S.thesis,School of Automation,Southeast University,China,2011.

[2]J.Li,Q.Sun,and X.Dai,“A coordination and optimization method for multi-bridge waterjet cutting processes,”inProc.42nd International Conference on Computers&Industrial Engineering,Cape Town,South Africa,pp.9575−9580,2012.

[3]X.Meng,J.Li,M.C.Zhou,and X.Dai,“Improved population-based incremental learning algorithm for scheduling multi-bridge waterjet cutting processes,”inProc.IEEE 11th International Conference on Networking,Sensing and Control(ICNSC),Miami,FL,USA,pp.496−500,2014.

[4]Q.Sun,“A colored traveling salesman problem and its application,”M.S.thesis,School of Automation,Southeast University,China,2013.

[5]J.Li,Q.Sun,M.C.Zhou,and X.Dai,“A new multiple traveling salesman problem and its genetic algorithm-based solution,”inProc.2013 IEEE International Conference on Systems,Man,and Cybernetics(SMC),Manchester,UK,pp.627−632,2013.

[6]J.Li,Q.Sun,M.C.Zhou,X.Yu,and X.Dai,“Colored traveling salesman problem and solution,”inProc.19th World Congress of the International Federation of Automatic Control,Cape Town,South Africa August 24−29,vol.47,no.3,pp.9575−9580,2014.

[7]J.Li,M.C.Zhou,Q.Sun,X.Dai,and X.Yu,“Colored traveling salesman problem.IEEE Transactions on Cybernetics,”vol.45,no.11,pp.2390−2401,2015.

[8]J.Li,X.Meng,M.C.Zhou,and X.Dai,“A two-stage approach to path planning and collision avoidance of multi bridge machining systems,”IEEE Transactions on Systems,Man and Cybernetics:Systems,DOI:10.1109/TSMC.2016.2531648.

[9]T.Bektas,“The multiple traveling salesman problem:an overview of formulations and solution procedures”Omega,vol.34,no.3,pp.209−219,2006.

[10]D.L.Applegate,R.E.Bixby,V.Chvátal,andW.J.Cook,“The traveling salesman problem,”Princeton:Princeton University Press,2006.

[11]N.Chakraborty,S.Akella,and J.T.Wen,“Coverage of a planar point set with multiple robots subject to geometric constraints,”IEEE Transactions on Automation Science and Engineering,vol.7,no.1,pp.111−122,2010.

[12]E.K.Xidias,P.Th.Zacharia,and N.A.Aspragathos,“Time-optimal task scheduling for two robotic manipulators operating in a three-dimensional environment,”Proceedings of the Institution of Mechanical Engineers.Part I:Journal of Systems and Control Engineering,vol.224,no.7,pp.845−855,2010.

[13]A.G.Gonzalez-Rodriguez and A.Gonzalez-Rodriguez,“Collision-free motion planning and scheduling,”Robotics and Computer-Integrated Manufacturing,vol.27,no.3,pp.657−665.

[14]R.Kala,“Multi-robot path planning using co-evolutionary genetic programming,”Expert Systems with Applicationsvol.39,no.3,pp.3817−3831,2012.

[15]H.Qu,K.Xing,and T.Alexander,“An improved genetic algorithm with co-evolutionary strategy for global path planning of multiple mobile robots,”Neuro computingvol.120,pp.509−517,2013.

[16]H.J.Yoon,“Scheduling for deadlock avoidance operation in robotic manufacturing cells,”Proceedings of the Institution of Mechanical Engineers,Part B:Journal of Engineering Manufacture,vol.224,no.2,pp.329−340,2010.

[17]T.S.Dahl,M.Mataric,and G.S.Sukhatme,“Multi-robot task allocation through vacancy chain scheduling,”Robotics and Autonomous Systems,vol.57,no.6−7,pp.674−687,2009.

[18]G.A.Korsah,B.Kannan,B.Browning,A.Stentz,and M.B.Dias,“xBots:an approach to generating and executing optimal multi-robot plans with cross-schedule dependencies,”inProc.IEEE International Conference on Robotics and Automation(ICRA 2012),St.Paul,MN,USA,pp.115−122,2012.

[19]T.Zheng and J.Li,“Multi-robot task allocation and scheduling based on fish swarm algorithm,”inProc.8th World Congress on Intelligent Control and Automation(WCICA 2010),Jinan,China,pp.6681−6685,2010.

[20]Y.Gan,X.Dai,and J.Li,“Cooperative path planning and constraints analysis for master-slave industrial robots,”International Journal of Advanced Robotic Systems,vol.9,no.88,pp.1−13,2012.

[21]G.Gutin,A.Yeo,and A.Zverovich,“Traveling salesman should not be greedy:domination analysis of greedy-type heuristics for the TSP,”Discrete Applied Mathematics,vol.117,no.1−3,pp.81−86,2002.

[22]D.S.Johnson and L.A.McGeoch,“The traveling salesman problem:a case study in local optimization,”Local Search in Combinatorial Optimization,E.H.L.Aarts and J.K.Lenstra(eds.),John Wiley and Sons,London,pp.215−310,1997.