Capture-aware Bayesian RFID Tag Estimate for Large-scale Identification

Haifeng Wu,Yang Wang,and Yu Zeng

I.INTRODUCTION

I NTERNET of things(IoT)has been considered as the third wave of world information industry,after waves of computer and internet.The purpose of IoT is to link realworld objects with virtual information and then to identify,track and manage all goods available [1]. IoT needs to be based on widely used sensors because plenty of objects’information is collected into network only by the sensors.Radio frequency identification(RFID)is a keystone of the sensors technology since small passive RFID tags make it possible to link millions and billions of physical products with virtual information.To enhance identification efficiency,the multiple tags in IoT need to be read quickly and the tags may simultaneously transmit their signals to the reader,which leads to collisions[2].Generally,an RFID system adopts anti-collision algorithms to solve the problem[3].Therefore,RFID tag anti-collision algorithm will play an important role in IoT.

In a passive RFID system,if two or more tags backscatter their signals to a reader simultaneously,a collision may happen and will disturb the identification[3],[4].However,two or more tags do not necessarily lead to collisions.Since the distances between the tags and the reader are different,the strengths of backscattered signals would also be different.The tag with stronger signal would be identified,and the weaker one would be missed.The phenomenon is called capture effect[5].Because capture effect is very common in an RFID system,optimal solution for the collision problem under capture effect has attracted much attention[5]−[8].

In the conventional anti-collision algorithms,a dynamic framed slotted Aloha(DFSA)algorithm is very popular[9]−[15].The algorithm configures an identification process with some continuous frames and each frame consists of slots.To achieve optimal identification efficiency,the frame will be dynamically adjusted according to the number of unidentified tags.Therefore,some new algorithms are proposed in recent years,but they do not take the capture effect into account.Here are several examples.Reference[16]presents the differential estimation problem to estimate the number of tags and the zero differential estimator(ZDE)is proposed to solve this problem without the capture effect.Reference[17]proposes an RFID estimation scheme with blocker tags(REB)while considering the privacy issue,but the phenomenon of capture effect is neglected.Reference[18]proposes a new scheme for estimating tag population size called average run-based tag estimation(ART),which is significantly faster than prior schemes regardless of the tag population sizes.But ART still does not take the capture effect into account.Under capture effect,however,the adjustment may not guarantee the optimal efficiency because the frame length is related not only to the number of tags but also to the occurrence probability of capture effect[7],and[8],[19],[20]have proposed algorithms to estimate the number of tags and the probability simultaneously.In general,both the number of tags and the probability of capture effect are unknown.Therefore,the number and the probability need to be estimated.For the problem,this paper proposes a novel algorithm called capture-aware Bayesian estimate.The contributions of this algorithm are summarized as follows.

1)Estimate the number of tags under large-scale RFID tag environment,where hundreds of tags or more are required to be identified at the same time.In the identification environment,the number of tags may be greater than an initial frame length of the DFSA algorithm.In this scenario,the estimation errors of existing algorithms will substantially increase.The proposed algorithm could reset the initial frame length from the first several slots in the initial frame.This guarantees that the estimation could be performed well via capture-aware Bayesian RFID tag estimate for large-scale identification under the large-scale tag environment.

2)Apply Bayesian rules[21]to estimate the number of tags and the probability of capture effect simultaneously.From three cost functions,three kinds of Bayesian estimates are derived.

From the numerical results,the estimation errors of the proposed algorithm are lower than those of conventional algorithms under the large-scale RFID tag environment with capture effect.Moreover,the identification efficiency from the proposed algorithm is also higher than that from the existing algorithms.

The rest of this paper is organized as follows.In Section II,the problems and related works are discussed.Section III describes identification efficiency and estimation under largescale tag identification.The capture-aware estimation for largescale identification is described in Section IV.The numerical results are shown in Section V.Finally,Section VI gives a conclusion.

II.PROBLEM DESCRIPTION AND RELATED WORKS

A dynamic framed slotted Aloha RFID algorithm configures an identification cycle with some continuous frames that consist of slots.Each tag responds at a random slot and only once in a frame.For a given time slot,there are only three possibilities:no tags,one tag,and more than one tag response.When capture effect does not occur,the three possibilities will result in an idle slot,a successful slot and a collision slot,respectively.The identification efficiency can be defined as the ratio between the duration of all successful time slots and total time slots.In DFSA algorithm,idle slots will increase when a frame length is too large.On the other hand,collision slots will increase when the frame length is too small.Both of them will lead to lower identification efficiency.Hence,the frame length requires to be dynamically adjusted for higher efficiency.When capture effect does not occur,the optimal frame length is only related to the number of tags[3],[10].In this scenario,we could estimate only the number of the tags.When capture effect occurs,however,the frame length is also related to the occurrence probability of capture effect.Thus,we need to estimate both the number of tags and the probability of capture effect.

Generally,a reader does not know the number of tags in its magnetic field before identifying,and an initial frame length in DFSA is set in advance.If the reader sets a very large value to the initial frame length,there must be excessive idle slots when the number of tags is less.Therefore,the value of length should be a compromise,e.g.,24in Q algorithm of electronic product code(EPC)C1Gen2[22],[23].Under large-scale tag environment,however,hundreds of tags or more need to be identified at the same time.The number of tags would be much larger than the initial frame length,which does not guarantee that the existing estimates perform well.

Vogt algorithm[10]is one of the estimates based on DFSA in RFID systems.The algorithm estimates the tag population by searching a minimum value between the observed and the expected number of the idle slots, successful slots and collision slots.However,the algorithm estimates only the number of tags frame length and does not consider the probability of capture effect.

Capture-aware backlog estimation algorithm(CMEBE)[7]adopts two-dimensional searches for a minimum value to estimate the tag population and the probability of capture effect simultaneously.Under large-scale tag environment,however,the number of tags would be much larger than the initial frame length.The minimum value may not exist at all.Capture-aware estimate(CAE)[8]could also estimate the tag population and the probability of capture effect simultaneously.Compared with CMEBE,CAE has lower computational complexity because it does not need to search for a minimum value.However,under large-scale RFID tags environment,the number of tags would be much larger than the initial frame length,and the number of idle slots in an initial frame is likely to be zero.CAE would be difficult to estimate the number of tags because the algorithm needs to compute the logarithm of the number of idle slots which must not be zero.

Maximum a posterior probability(MAP)algorithm[19]also searches for an extremum value to estimate the number of tags and the probability.Like CMEBE,MAP would not find a global extremum value,either when it is applied to largescale RFID tag environment.

Bayesian method is not new[21].Reference[13]has proposed three Bayesian methods to estimate the tag population.However,these methods take only the tag population into account.Reference[20]proposes a minimum mean square error(MMSE)method to estimate the tag population in large-scale RFID tag environment.In fact,the estimate could be derived by Bayesian method.This paper proposes three Bayesian estimates,which take both the number of tags and the probability of capture effect into account.Furthermore,the proposed methods could adapt well to the large-scale tag environment.

III.IDENTIFICATION EFFICIENCY AND ESTIMATION UNDER LARGE-SCALE TAG IDENTIFICATION

Ift0,t1andtkdenote the duration of an idle,successful and collision slot,respectively,the expected identification efficiency of a frame in a dynamic ALOHA can be defined as[10]−[12]

whereE(·)denotes an expected function,a0,a1andakdenote the expected numbers of idle,successful and collision slots,respectively and could be given by[7]

in whichαdenotes the probability of capture effect,andare the expected number of slots where no tags,one tag and at least two tags(k≥2)respond,respectively.From[10]−[12],andcan be given by

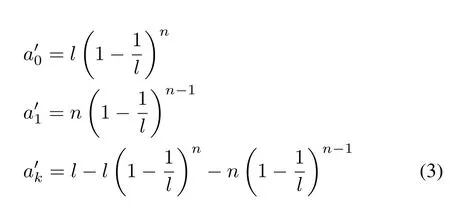
whereldenotes the frame length andndenotes the number of tags.In order to obtain the optimal identification efficiency,we have the optimal frame length

whereLdenotes the search range ofl.Substituting(2)and(3)into(1),we can find thatPsis in facta function ofnandα.Generally,the values ofnandαare unknown in advance.Therefore,we need to estimate them to obtain the optimal frame length in(4).

Vogt algorithm[10]estimates the number of tags from

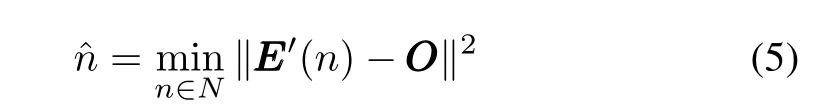
In(5),Vogt only estimates the number of tagsnand does not consider the probability of capture effectα.It sets the frame length byl=n[2].From(4),Vogt is difficult to obtain the maximum identification efficiency withoutα.

CMEBE estimates the number of tags and the probability of capture effect by

whereandNdenote the search range ofαandn,respectively.From(6),CMEBE needs the 2D searches for a minimum value ofUnder large-scale tags identification environment,the number of tags may be much greater than an initial frame length,and the number of idle slotsc0in the frame is likely to be zero.In this scenario,in(6)may not have a minimum value.Let

We give a 3D surface ofεabout searchingαandnin Fig.1.In the figure,the initial frame length is 128,the number of tags number is 800 and the probability of capture effect is 0.5.From Fig.1,there is no global minimum value ofεat all.Further,Fig.2 gives the 2D cross-sections close to the canyon of the curve surfaceεin Fig.1 whenαis 0.4,0.5 and 0.6,respectively.From Fig.2,we can see that both the curvesεofα=0.5 and 0.6 decrease monotonously withn.Although the curveεofα=0.4 has a minimum value,the value is not global.

CAE algorithm[8]estimates the number of tags by

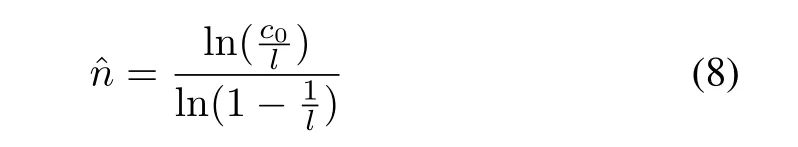
and then estimates the probability of capture effect from(2)[8].Since(8)does not need to search a minimum value like Vogt,CMEBE and CAE have lower computational complexity.When the number of tags is much greater than an initial frame length,however,the number of idle slots is likelyc0=0 and we would not figure out ln(c0/l)in(8).Thus,CAE is also difficult to be applied to the large-scale tag identification.Next,we will propose our estimation method.The proposed method would accurately estimate the number of tags and the probability of capture effect even when the number of tags is much greater.

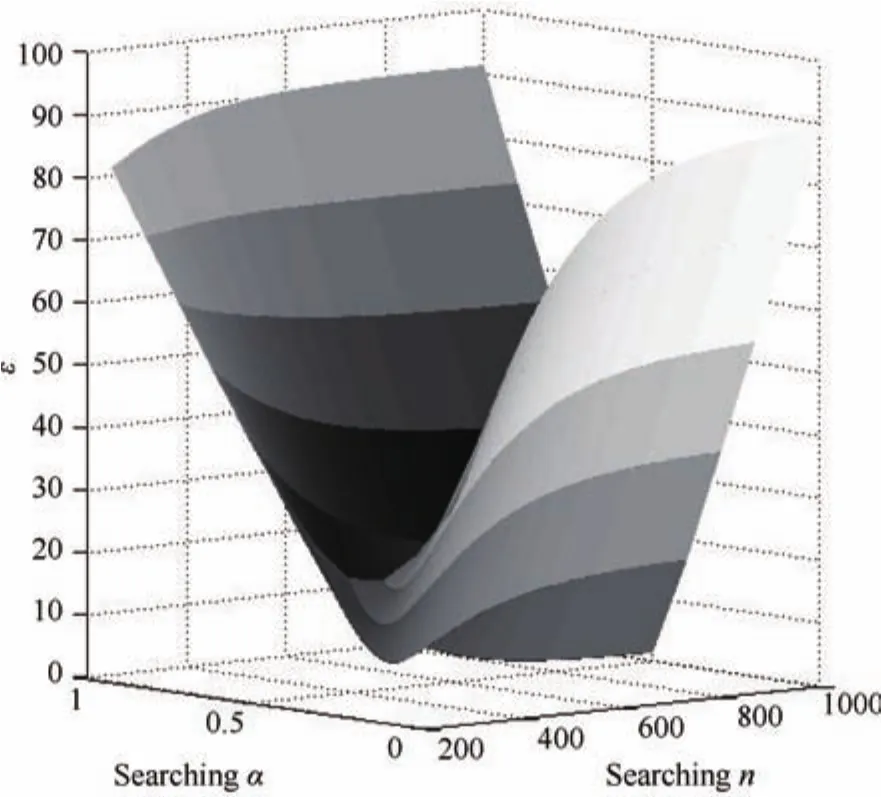
Fig.1.εin(7)about searching number of tags and probability of capture effect when l=128 and n=800.

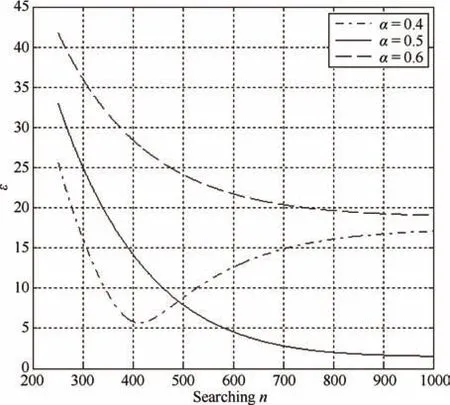
Fig.2.2D cross-sections close to the canyon of the curve surfaceεin Fig.1.

IV.CAPTURE-AWARE ESTIMATION FOR LARGE-SCALE IDENTIFICATION

A.Setting Initial Frame for Large-scale Identification

In large-scale identification,it is very likely that the tag population in the magnetic field of a reader is much larger than an initial frame length,i.e.,n≫l0.Thus,the number of idle slots would bec0=0.From the analysis in Section III,the reason why CMEBE and CAE are not applied to the large-scale tags identification isc0=0.Intuitively,we can lengthen the frame lengthl0untilHowever,how can we obtainc0?Generally,c0is obtained only after the frame completing.If,it will produce many collision slots after the frame completing.This will cause lower identification efficiency.Actually,we could predict whetherc0=0 or not from only the first several slots in the frame.Hence,excessive collision slots would be reduced.Next,we will describe the method.

Given one of slots in a frame ofl,the probability that the slot is idle,successful or collision can be shown as

wherej=0,1 andk,respectively.In DFSA,when the tag population isnand the frame length isl,the probability that the firstmslots are all non-idle is given as

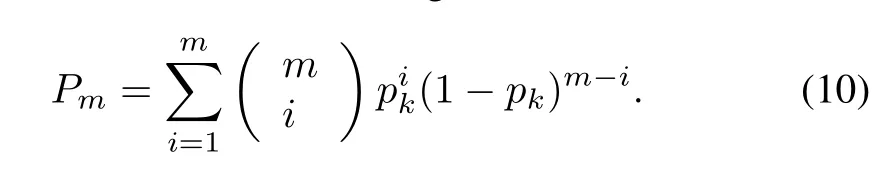
Table I gives the theoretical and experimental results ofPm,m=1,2,3,4 and 5whenl=128,α=0.5 andnvaries from 100 to 1000.The theoretical values are computed from(10)and the experimental values are the ratio of the number of the experiments where there is not less than one collision slot in the firstmslots and the total number of the experiments.From the table,all the values ofPmwill increase withn,regardless ofm.Especially,Pmis very close to 1 with a larger value ofmwhenn=1000.The results indicate that the probability that there is not less than one collision slot in the firstmslots increases with a larger value ofn.When it is in large-scale RFID tags environment,Pmis close to 1withm＞2.Hereby,the initial frame length can be set to

whereKis an integer greater than one,which ensures thatthe frame length becomes larger.But it does not mean thatKshould be as large as possible.Because if the frame length is too large,there will be more idle slots,which will increase the identification time and lower the performance of the algorithm.

TABLE I PROBABILITY OF NOT LESS THAN ONE COLLISION SLOT IN THE FIRST m SLOTS WHEN l0=128 ANDα=0.5

The method called self-adjusted frame length ensures the rationality of the initial frame length.Fig.3 gives the self adjusted frame length whenl0=128,n=600,m=3,K=2,0≤α≤1.The settings of initial frame length of Vogt,traditional Bayes,CMEBE and CAE algorithms mentioned in the paper all can be seen from Fig.3.Besides,Fig.3 gives two optimal lengths computed by(4)undert0=t1=tkandt0/=t1/=tk,respectively,and system parameters of the latter are specified in EPC C1 Gen2,which can be referenced to[23].From Fig.3,we can see that Vogt and traditional Bayes’curves remain unchanged whenαincreases,and CMEBE and CAE’s curves ascend far away from the curve of optimal length whenasαdecreases.On the other hand,the curve of self-adjusted frame length always comes close to the optimal lengths regardless of the value ofα.As a matter of fact,the proposed method can make sure the rationality of the initial frame length regardless ofα.

Fig.3.The frame length when l0=128,n=600 and 0≤α≤1.

Note that we judge whether there is more than one collision slot in the firstmslots instead of being all collision slots like the method in[22].The reason is that capture effect may occur in a slot.Even if the slot has more than two tag responses,this slot also can be a successful slot.

B.Bayesian Estimate

From the subsection above,our method requires to judge the three slots iteratively.This may produce identification more times if the iterations are more.The value of probability among frames may be time-variant,e.g.,mobile environment.Consider the environment without mobile identification,the probability may be slowly time-variant.Thus,we can estimate the tag and capture effect probability,and then set the next frame length from the estimated value.The duration of the followed self-adjusted frame length from the first three slots can be shortened because the iterations may be reduced.For the mobile environment,surely,self-adjusted step will be more important.

In this subsection,we will propose the Bayesian estimate.It could estimate both the number of tagsnand the probability of capture effectα.Hence,we call the proposed estimate captureaware.The estimate could be given as

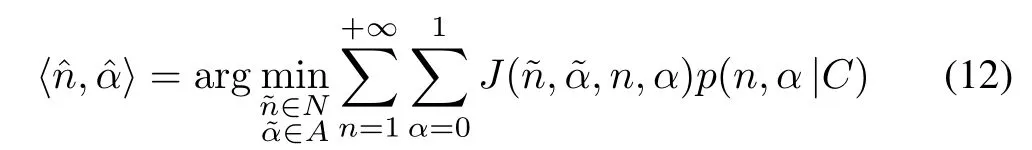
whereis a cost function,is a probability w.r.t.nandαunder condition

and could be computed by[15]

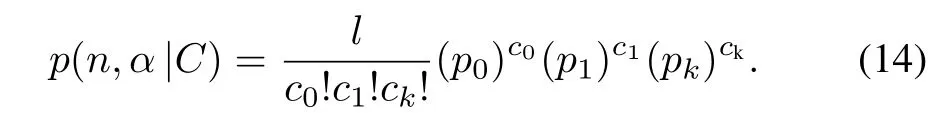
The search range of setNandAare given as

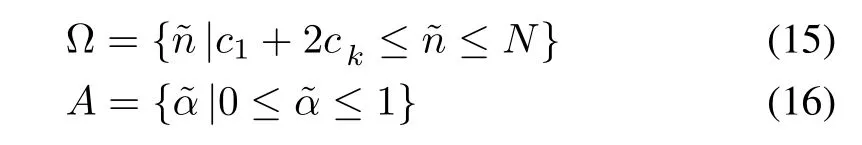
respectively whereNis the maximum number of tags read by the RFID system.

According to(12),different Bayesian estimates have different cost function.Here,we choose the following three kinds of cost functions.The cost function of capture-aware Bayesian mean square estimate(CBMS)is given as

Substitute(17)into(12),compute the first partial derivatives of ñ and ã,respectively and let them be zeros.Then,we can obtain the estimated values shown as

where

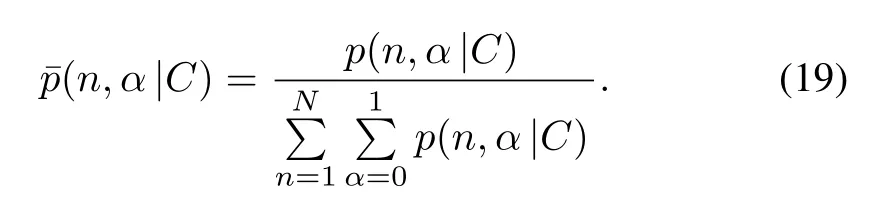
Equation(18)has the same form as(14)in[20].That is,MMSE could be derived by Bayesian method under the cost function(17).The cost function of capture-aware Bayesian absolute estimate(CBAV)is given as

Likewise,substituting(20)into(12),we can obtain the estimate values given as

The cost function of capture-aware Bayesian uniform estimate is given as

where Δ is a very small constant.Substituting(22)into(12),we give the estimate

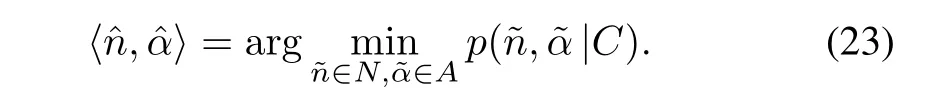
The estimate in(23)has the same form as a maximum posterior probability estimate[19].Thus,we could also call it capture-aware maximum posterior probability estimate(CMAP).

C.Frame Length Adjustment

How to adjust a frame length in DFSA is discussed in[6],[7],[11],[12].A ll of the methods assume that the three kinds of slots,i.e.,idle,collision and successful slots have the equal durations.However,in real RFID systems,such as EPC C1 Gen2 standard[23]and ISO 18000-6[24],[25],each kind of slot does not have the same duration.Further,[11],[12]do not consider the impact of capture effect on the frame length adjustment.Here,we consider the frame adjustment under different durations of the three types of slots and capture effect.We take a linear model into account.That is,l=rn[14].Then,we can obtain

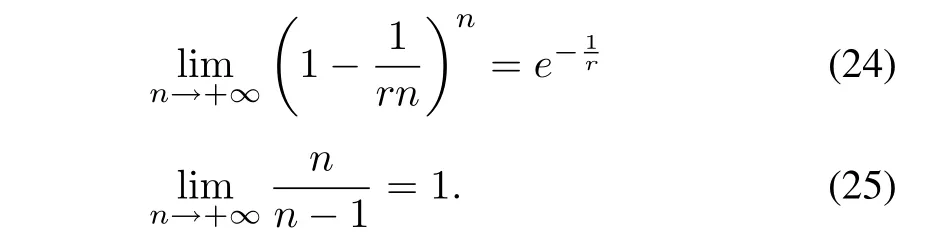
We substitute(2),(24)and(25)into(1),and letβ=t0/t1,Then,the identification efficiency is given by

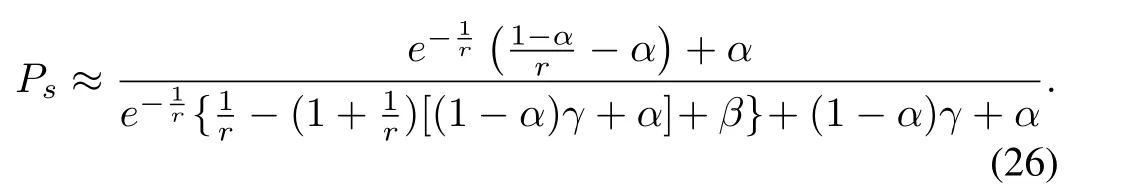
Let(26)be maximized,and we have

where R is the search range ofr.Then,the optimal frame length can be given as

D.Description of the Algorithm

In the proposed algorithm,an identification cycle is described as follows and the pseudo-code operation of a reader is shown in Algorithm 1.

Initially,the reader sets a frame length tol0and implements a functionInterrogate(·)to transmit a query command withl0.Tags will randomly select slots in the initial frame to respond.If the firstmslots are all non-idle,we setl0=K l0from(11)and the tags will re-select slots.If not,the reader will implement the functionInterrogate(·)with the set value ofl0and count all of idle slots,successful slots and collision slots in the frame.Then,the reader implements a functionto estimate the tag population and the probability of capture effect by(18),(21)or(23).The next frame length is adjusted from(28)with the estimated results above.

Finally,the reader judges whether all tags are identified or not.If the number of collision slots is zero,no tags need to be identified.Thus,the identification cycle ends.

V.NUMERICAL RESULTS

A.System Setup

In this section,we give the numerical results to verify the performance of proposed algorithm.In numerical experiments,we consider a scenario with a single reader and a set of passive tags that enter the reader’s zone and do not leave until all the tags are successfully identified.Numerical results are from Monte Carlo method and each result is the mean of 500 independent experiments.We compare the proposed CBMS,CBAV and CMAP estimate with the existing Vogt,traditional Bayes,CMEBE,CAE and MMSE algorithm,which are as follows:

1)CBMS:Capture-aware Bayesian mean square estimate derived from(19).

2)CBAV:Capture-aware Bayesian absolute value estimate derived from(21).

3)CMAP:Capture-aware Bayesian maximum posterior probability estimate derived from(23).

4)Vogt,traditional Bayes,CMEBE,CAE and MMSE are the algorithms in[7],[8],[10],[13],[20],respectively.Note that CAE requires computing the logarithm of the number of idle slots in a frame.Hence,the estimated value will be∞when the idle slot is zero.In practice,however,the number of tags could not be infinite.To assure CAE to have an estimated value in this case,the value is chosen as the upper bound of a set,N,i.e.,Nwhich is the same as in Vogt and CMEBE above.

Parameter settings of above algorithms are as follows:

1)The initial frame length isl0=128.

2)The search range of the tag population isN={c1+2ck≤n≤N|n∈Z},whereN=1000.

3)The search range of the probability of capture effect isA={0,0.1,0.2,...,1.0}.

4)m=3,i.e.,setting the frame length from the first three slots.

5)K=2,i.e.,the set frame length is twice length than before.We choose 2 instead of other larger integer,because larger adjusted frame length will lead to more idle slots.

6)The durations of each kind of slots aret0=50µs,t1=400µs andtk=200µs[13],respectively.

Here,we give the details of the choice ofm=3 andK=2 in the experiment.Fig.4 gives the comparison of self-adjusted frame length under different values ofmandK,and the other parameters arel0=128,n=600 and 0≤α≤1.As we can see from Fig.4,the curve of optimal length descends asαincreases,also do the curves under different values ofmandK.From Fig.4,whenα＜0.6,the curve ofK=2 andm=3 is more close to the curve of optimal length than the others.Besides,whenα＞0.8,the curve ofK=2 andm=3 is close to the curve of optimal length like that ofK=2 andm=4 andK=4 andm=4.Though the curve ofK=2 andm=3 is not good than the two curves ofK=2 andm=4 andK=4 andm=4 when 0.6＜α＜0.8,it is still not far from the curve of optimal length.From Fig.4 and Table I,we find that the set ofK=2 andm=3 would be a good choice.

Fig.4.Comparison of self-adjusted frame length under different values of K and m.

B.Estimation Errors

In this subsection,we measure the error of estimating the number of tags in a frame.The error for the number are defined as

whereˆnandndenote the estimation and the actual value of tags,respectively.

Fig.5 shows the estimation errorseof tag population for Vogt,traditional Bayes,CMEBE,CAE,MMSE,CBMS,CBAV and CMAP,respectively whenn=200 and the probability of capture effect varies from 0.1 to 1.From the figure,the curves are very close to each other and approximately between 3%and 8%except for Vogt and traditional Bayes.The two curves increase in value with the probability of capture effect.The results show that the proposed estimate,MMSE,CMEBE and CAE can all estimate the tag population accurately when the tag population is not greater than the initial frame length.Further,MMSE and CBMS have the same curve because MMSE is actually a Bayesian estimate when the cost function is a mean square error function.Moreover,the performances of proposed algorithms are a litter better than the others’whenα＜0.8.On the other hand,the estimation errors of Vogt and traditional Bayes are much more,especially when the probability is beyond 0.2.The reason is that the two algorithms do not consider the capture effect,while the other estimates have the capture-aware estimation.

Fig.6 shows the estimation errorseof the above algorithms whenn=600 and the other parameters are chosen the same as Fig.5.From the figure,CMEBE and CAE’s curves fluctuate between 18%and 31%while the proposed estimate curves are no more than 15%and much lower than the two former estimates.In addition,MMSE is also an algorithm with lower estimation errors and has the same curve as of CBMS.On the other hand,the estimation errors of Vogt and traditional Bayes are still much more and increase from 25%to 80%.

The reason is that,the proposed estimates consider the number of idle slotsc0=0 in large-scale identification environment.Although CMEBE and CAE could be aware of capture effect,on the contrary,they do not work better whenc0=0.

Fig.5.Estimation errors of tags(l=128,n=200,K=2,m=3).

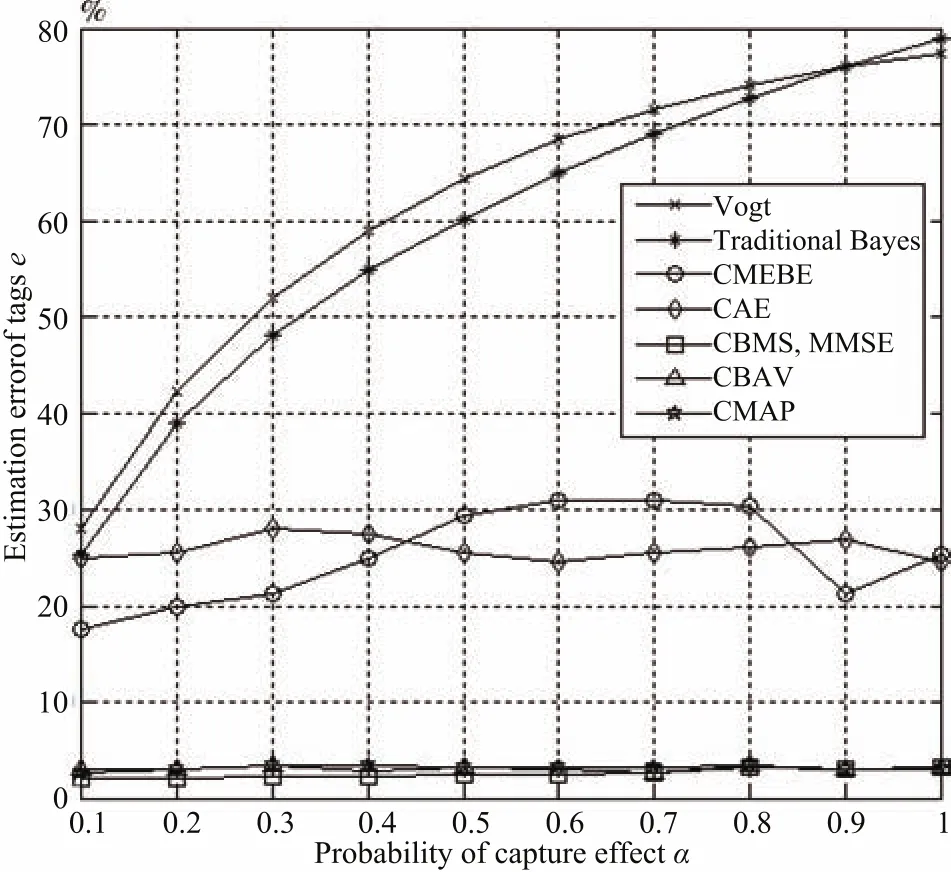
Fig.6.Estimation errors of tags(l=128,n=600,K=2,m=3).

C.Identification Efficiency

In this subsection,we will demonstrate the comparison of identification efficiency of each algorithm.Fig.5 gives the identification efficiencies of Vogt,traditional Bayes,CMEBE,CAE CBMS,CBAV and CMAP,where the frame length is adjusted from the estimated values of the algorithms above,respectively.The identification efficiency is given by

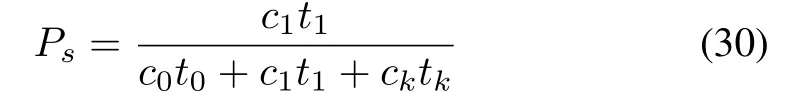
and the tag population isn=600.From the values oft0,t1andtk,we can getβ=0.125 andγ=0.5.The optimal frame length adjustments in the algorithms above are as follows.

The adjustment in Vogt is[10]

The adjustment in traditional Bayes is[13]

CMEBE and CAE adopt the same adjustment[7],[8]

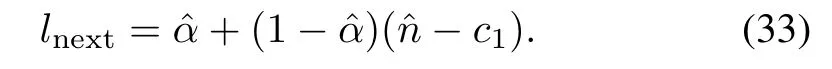
The adjustments in CBMS,CBAV and CMAPare from(31)−(33).The result values are given in Table II.

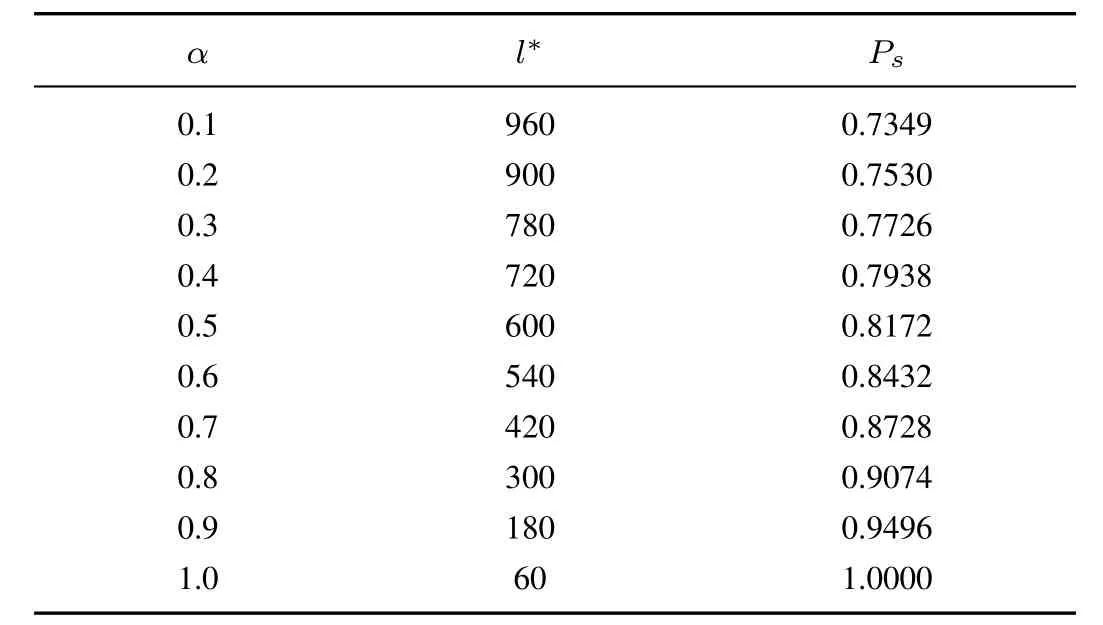
TABLE II THE VALUES OF Ps AND l∗WHEN n=600

From Fig.7,the curves ranging from the highest to the lowest are,the proposed algorithm curves,CMEBE and CAE curves,and traditional Bayes and Vogt curves.From the result,the algorithm’s identification efficiencies are related to their estimation errors.The algorithm with lower estimation error has higher identification efficiency,while the algorithm with higher estimation error has lower identification efficiency.Moreover,CBMS,CBTV and CMAP set the optimal frame length based on non-isometric time slots.Therefore,the results also show that the method of non-isometric times lots performs better than that of isometric slots.And with the self-adjusted frame length method,the frame length can be close to the optimal length in each frame including the initial frame length,which visibly improves the identification efficiency.

V I.CONCLUSION

In DFSA algorithms,we consider the influence of both capture effect and large-scale identification on the performance of RFID identification efficiency.For this reason,we propose the novel Bayesian estimates,CBMS,CBTV and CMAP.From our derivation,it is proved that the conventional estimate MMSE and MAP estimate are actually Bayesian estimates and could be obtained from CBMS and CMAP by different cost functions.The numerical results show that the estimation performance of the proposed algorithms is close to that of conventional algorithms when the tag population is small.Under large-scale RFID tags environment,however,the estimation errors of proposed algorithm are obviously lower than those of conventional algorithms.In addition,we derive the optimal frame length under different durations of an idle slot,a collision slot and a successful slot.The numerical results show that,the identification efficiency of the proposed frame length is higher than that of conventional algorithms.It can be deduced from the identification efficiency performance that the proposed estimation method would adapt better to the largescale RFID tags environment with capture effect.

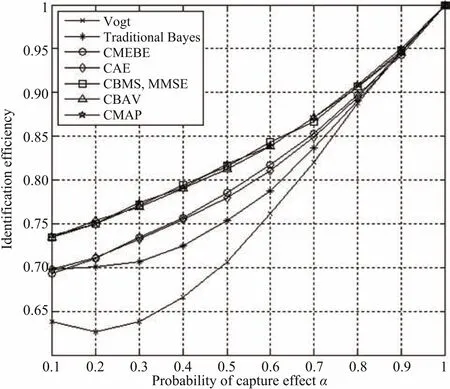
Fig.7.Identification efficiency(l=128,n=600,K=2,m=3).

[1]E.Welbourne,L.Battle,G.Cole,K.Gould,K.Rector,S.Raymer,M.Balazinska,and G.Borriello,“Building the internet of things using RFID:The RFID ecosystem experience,”IEEE Int.Comput.,vol.13,no.3,pp.48−55,May−Jun.2009.

[2]Q.J.Xiao,S.G.Chen,and M.Chen,“Joint property estimation for multiple RFID tag sets using snapshots of variable lengths,”inProc.17th ACM Int.Symp.on Mobile Ad Hoc Networking and Computing,New York,USA,2016,pp.151−160.

[3]D.H.Shin,P.L.Sun,D.C.Yen,and S.M.Huang,“Taxonomy and survey of RFID anti-collision protocols,”Comput.Commun.,vol.29,no.11,pp.2150−2166,Jul.2006.

[4]X.L.Jia,Q.Y.Feng,and C.Z.Ma,“An efficient anti-collision protocol for RFID tag identification,”IEEE Commun.Lett.,vol.14,no.11,pp.1014−1016,Nov.2010.

[5]Y.C.Laiand L.Y.Hsiao,“General binary tree protocol for coping with the capture effect in RFID tag identification,”IEEE Commun.Lett.,vol.14,no.3,pp.208−210,Mar.2010.

[6]Y.Maguire and R.Pappu,“An optimal Q-algorithm for the ISO 18000-6C RFID protocol,”IEEE Trans.Automat.Sci.Eng.,vol.6,no.1,pp.16−24,Jan.2009.

[7]B.Li and J.Y.Wang,“Efficient anti-collision algorithm utilizing the capture effect for ISO 18000-6C RFID protocol,”IEEE Commun.Lett.,vol.15,no.3,pp.352−354,Mar.2011.

[8]X.Yang,H.F.Wu,Y.Zeng,and F.Gao,“Capture-aware estimation for the number of RFID tags with lower complexity,”IEEE Commun.Lett.,vol.17,no.10,pp.1873−1876,Oct.2013.

[9]F.Schoute,“Dynamic frame length A loha,”IEEE Trans.Commun.,vol.31,no.4,pp.565−568,Apr.1983.

[10]H. Vogt, “Efficient object identification with passive RFID tags,” inProc.Int.Conf.Pervasive Computing,Berlin,Heidelberg,Germany,2002,pp.98−113.

[11]S.R.Lee,S.D.Joo,and C.W.Lee,“An enhanced dynamic framed Slotted ALOHA algorithm for RFID tag identification,”inProc.Int.Conf.Mobile and Ubiquitous Systems:Networking and Services,Washington,DC,USA,2005,pp.166−174.

[12]W.T.Chen,“Optimal frame length analysis and an efficient anticollision algorithm with early adjustment of frame length for RFID systems,”IEEE Trans.Veh.Technol.,vol.65,no.5,pp.3342−3348,May 2015.

[13]M.Mayerand N.Goertz,“RFID tag acquisition via compressed sensing:Fixed vs.random signature assignment,”IEEE Trans.Wirel.Commun.,vol.15,no.3,pp.2118−2129,Mar.2015.

[14]G.Khandelwal,A.Yener,K.Lee,and S.Serbetli,“ASAP:A MAC protocol for dense and time constrained RFID systems,”inProc.IEEE Int.Conf.Communications,Istanbul,Turkey,2006,pp.4028−4033.

[15]C.P.Wong and Q.Y.Feng,“Grouping based bit-slot ALOHA protocol for tag anti-collision in RFID systems,”IEEE Commun.Lett.,vol.11,no.12,pp.946−948,Dec.2007.

[16]Q.J.Xiao,B.Xiao,and S.G.Chen,“Differential estimation in dynamic RFID systems,”inProc.IEEE INFOCOM,Turin,Italia,2013,pp.295−299.

[17]X.L.Liu,B.Xiao,K.Q.Li,J.Wu,A.X.Liu,H.Qi,and X.Xie,“RFID cardinality estimation with blocker tags,”inProc.IEEE Int.Conf.Computer Communications,Kowloon,China,2015,pp.1679−1687.

[18]M.Shahzad and A.X.Liu,“Fastand accurate estimation of RFID tags,”IEEE/ACM Trans.Netw.,vol.23,no.1,pp.241−254,Feb.2015.

[19]X.Yang,H.F.Wu,Y.Tan,and R.Q.Lin,“Improving the performance of RFID tag anti-collision for capture effect,”Appl.Mech.Mater.,vol.416−417,pp.1484−1488,Sep.2013.

[20]Y.Wang,H.F.Wu,and Y.Zeng,“Capture-aware estimation for largescale RFID tags Identification,”IEEE Signal Process.Lett.,vol.22,no.9,pp.1274−1277,Sep.2015.

[21]F.Shen,Z.Ye,and Y.Qian,Statistics and Process of Signal.Hefei:China University of Science and Technology Press,2003,pp.389−392.

[22]Y.H.Cui and Y.P.Zhao,“A modified Q-parameter anti-collision scheme for RFID systems,”Proc.Int.Conf.Ultra Modern Telecommunications and Workshops,St.Petersburg,Russia,2009,pp.1−4.

[23]EPCglobal ClG2,“EPC radio-frequency identification protocols class-1 generation-2 UHFRFID protocol for communications at860MHz−960 MHz,”EPC global Inc,2008.

[24]ISO,“Information technology — radio frequency identification(RFID)for item management—Part 6:Parameters for air interface communications at 860 MHz to 960 MHz,”International Standard ISO/IEC 18000-6,2004.

[25]ISO,“Information technology — radio frequency identification(RFID)for item management—Part 6:Parameters for air interface communications at 860 MHz to 960 MHz,Amendment1:extension with type C and update of types A and B,”International Standard ISO/IEC 18000-6,2006.