An Intrusion Detection Algorithm for Wireless Networks Based on ASDL

Weijun Zhu,Miaolei Deng,and Qinglei Zhou

I.INTRODUCTION

INTRUSION detection(ID)is an important network security technique.Compared with the anomaly ID methods,the misuse ID ones cannot report unknown types of attacks.However,the latter methods have a comparatively low false positives rate with regard to known types of attacks.This is due to the principle of misuse intrusion detection:intrusion detection systems(IDS)developers predefine their known types of attacks,use appropriate language to describe these types,and establish libraries of attack patterns(called misuse signatures).The system will monitor the audit log.Once adata stream in the log is found to match with certain attack type,it means that an attack is found.

However,such a class of detection methods based on pattern matching(PM)suffers from their inherent problems,such as the lack of power of detecting various changing attack patterns[1],[2].To address these issues,a series of intrusion detection methods based on model checking[3]have been developed in[1],[2]and[4].Their basic principle can be formulated as follows:1)use a temporal logic formula to describe an attack pattern as well as an automaton to record what happened in the audit log;and 2)use a model checking algorithm to check whether the automaton satisfies the formula(i.e.,whether the records match the pattern).The logical constructs in temporal formulas can flexibly describe various logical relationships between attack actions.

Compared with the PM-based approaches,the MC-based ones can effectively portray the ever-changing attack patterns[1],[4].Furthermore,the MC-based approaches have an important advantage for intrusion detection over the PM-based ones.Pattern matching is usually applicable to detect inconsistencies between data while automata,temporal logic formulas and model checking techniques are applicable to detect inconsistencies of behaviors. Thus, the MC-based methods can do something more than the PM-based ones since intrusion attacks involve complex behaviors besides the comparatively simple data[5].

Linear temporal logic(LTL)and interval temporal logic(ITL)are employed to describe network attacks,respectively in[1],[2]and[6].However,these logics cannot describe a large number of complex repeated attacks and coordinated attacks,due to their insufficient expressive ability.In particular,a coordinated attack usually consists of multiple attacks on the same target.It is usually launched by multiple attackers under a unified strategy.A coordinated attack consists of many dispersed behaviors.And none of them is believed to be a danger by IDS algorithms.However,their combination may be fatal to a target.Furthermore,there are a large number of concurrent processes and their synchronized communication(communication for short),cannot be modeled conveniently,such a complex attack gets concealed in this way.

For example,a famous coordinated password cracking tool called Driver allows many machines in different subnets to collaboratively use a unified strategy to launch password guessing.It invokes various machines to scan available proxy servers,and assigns at least one agent to every machine in order to guess password.Even in every half second,driver makes a different machine send a password connection.In this way,a process of password guessing is greatly accelerated,and it does not result in any address conflict.Asa result,these attacks which are launched in a cooperative manner,are hard to detect with traditional IDS methods which handle local rules rather than global rules.Fig.1 provides us a brief sketch on the main points of this scenario.Fig.2 illustrates a scenario of a coordinated password guessing.See Section IV-B for more details on coordinated password guessing.

Fig.1.A roadmap to the open issue.

Fig.2.An illustration of scenario for a coordinated password guessing,which can be found by none of the existing MC-based IDS methods due to none of them are collaborative.

In order to detect some coordinated attacks,collaborative intrusion detection systems have been proposed to correlate suspicious evidence between different IDSs to improve the power of intrusion detection[7].Global correlation rules are important to collaborative IDSs,since these rules can be employed to find some unified attack strategies.However,the existing methods,based on the global rules that are applied for descriptions of coordinated attacks,are still not strong enough under some conditions.[7]and[8]give more intuitive examples on coordinated attacks in order to identify this issue.In particular,none of the existing MC-based methods is collaborative as yet,which has a direct consequence that no coordinated attack can be detected by the MC-based methods.

Therefore,motivated by detecting complex coordinated attacks,we,in this paper,present a new temporal logic language called ASDL to describe synchronization communications in network attacks.On the basis of it,an intrusion detection method is presented.The results of simulations show that:the new approach can detect the coordinated attacks with synchronization phenomenon,whereas the existing MC-based approaches cannot do it.This is the main contribution of this paper.

The rest of this paper is organized as follows.Section II illustrates some related works and compares them with the new approach.Section III introduces ASDL.Section IV uses ASDL programs to establish a series of models for some attack patterns,and some cases are given in this section.Section V explores the power of some constructs in ASDL in order to study the ability of the new attack models.An ASDL model checking algorithm and its misuse intrusion detection algorithm are formalized in Section VI.Section VII conducts some simulations and compares the new algorithm with the existing ones with regard to the detection capabilities for some types of intrusion attacks.Section VIII draws the conclusions of this paper.

II.RELATED WORKS

A.Detect Various Attack Types Using Model Check of the Temporal Logics Without Interval Construct

A tool called ORCHIDS was developed[4],which fulfilled the LTL-model-checking-based method for intrusion detection in reality[1].In one experiment,ORCHIDS found some p-trace attacks[9]which usually exploit the flaws in calls between processes to inject some malicious codes.It is difficult for traditional intrusion detection systems to find this type of attacks because they only match individual events[9].The ORCHIDS was improved in[10].In a real environment,it successfully detected a series of wireless network attacks[10],including de-authentication flooding,rogue access points,and Chop-Chop.This is the first IDS to successfully detect Chop-Chop attacks[10].Furthermore,in order to avoid repeated verifications needed by the algorithm in[1],[11]put forward an improved algorithm,which is able to compute the number of guesses in password attacks.

Furthermore,some extended versions of the LTL model checking technique can be also applied to detect intrusion attacks,such as an IDS approach based on the probabilistic LTL model checking which is presented in[12]and an extension of LTL with the past constructs for intrusion detection[13].

Computation tree logic(CTL)is another temporal logic without any interval construct.Different from LTL,CTL offers a formalism to express some branch properties.In fact,the CTL model checking can be applied to detect some network attacks,such as the intrusion behaviors for a zero know ledge system and the sliding window protocol,as shown in[14]and[15],respectively.

Compared with the methods mentioned above,our algorithm in this paper can be used for detecting some coordinated attacks.This is due to the fact that the logic embedded in the new algorithm has an await statement,a frame statement and a projection star statement,and these statements can describe some synchronization communications among concurrent processes in an attack(See Section III-B and Section VII).

B.Detect Various Attack Types Using Model Check of the Temporal Logics With Interval Constructs.

ITL was put forward in[16].With its successful and broader adoption and adaptation,ITL is becoming a class of logics,including some non-real-time interval logics[16]and some real-time interval logics[17]−[19].These temporal logics have the more expressive ability than LTL since all of the former logics have some interval constructs.That is to say,various constructs in these logics are put forward to express some interval properties.For example, “;”, “∗”,“prj”and “prjΘ”are the four interval constructs of the logic presented in this paper(see Table I for their intuitive meaning,or Definition 6 and Definition 7 for their formal definitions).

There are some studies that use the interval temporal logics for describing some attack patterns so that more intrusion behaviors can be expressed[6],[20],[21].However,these papers do not mention how to detect these attacks automatically.The methods presented in[2]and[5]can do it automatically.However,these methods cannot be applied to detect coordinated attacks.In comparison,the algorithm presented in this paper can overcome this flaw.This is due to the fact that the logic embedded in the new algorithm has an await statement, a frame statement and a projection star statement,and these statements can describe some synchronization communications among concurrent processes in an attack(See Section III-B and Section VII.)

C.Detect Malware Using Model Checking

Some studies,such as[22]−[27],employed the model checking technique to detect malicious behaviors in software.These methods detect antivirus in local software,not cyberattacks.

D.More Studies on Network Attacks and Defenses Using Model Checking

There are some different studies in this area.[28]employed a LTLmodel checker to successfully detect some errors in the signatures of IDS.[29]constructed a model for an intrusion system of an EPC network using a timed automaton,and it verified the correctness of the model in terms of the model checking tool UPPAAL.[30]showed that the model checking technique can decide whether or not a potential attack scenario of a cardiac implantable medical device is the source of the patient’s death.However,these methods do not detect any network attack directly.

III.ASL AND ASDL

A.ASL

A real-time interval logic called real-time attack signature logic(RASL)was presented in[5]for detecting various realtime concurrent attacks.We can get an interval logic called attack signature logic(ASL)by deleting the real-time constructs from RASL,so that some concurrent attacks without time constraints can be described by ASL.

The formal definitions of ASL are formalized in the Appendix A.And the main ASL formulas and their intuitive meaning are illustrated in Table I.

We will employ Fig.3 to illustrate the ASL formulas via an example in realworld,i.e.,the password guessing.Comparing Table I with Fig.3,we can further understand the intuitive meaning of the ASL formulas.

B.ASDL

Similar to ASL,projection temporal logic(PTL)given by[31]−[33]is another interval temporal logic which has an executable subset called modeling,simulation and verification language(MSVL)(see[34]and[35]).The MSVL is a temporal logic language which can describe synchronization communication.However,MSVL programs are not suitable for modeling network attacks due to the complex constructs embedded in MSVL.Therefore,we present an executable revised version of ASL,i.e.,ASDL.

The formal definitions of ASDL are for mulized in the Appendix A.And the main ASDL statements and their intuitive meaning are illustrated in Table II.

There are fourteen basic statements in ASDL,and an ASDL program can be obtained by calling recursively these fourteen ones.One can grasp the intuitive meaning of the ASDL statements by comparing some sketch and an example in real world in Fig.3,Table I and Table II.See Definition 10 for formal description of the relationship between these statements and the ASL formulas.

It is noticeable that a frame statement calledframe(x)is defined in ASDL.This statement is used for declaring that the values of the variablexare automatically inherited in the whole interval.On the basis of it,the await statement can be further defined for realizing synchronous communication among processes.

In brief,an ASDL statement corresponds to a formula in a decidable subset of the first order version of ASL.The formulas in this subset can be replaced by some ASL formulas in this way,as shown in the proof of Lemma 3 and Lemma 4.The execution of an ASL program means that it is looking for an interval in which the ASL formula can be satisfied.An ASDL program is executed successfully if its corresponding formula in ASL is satisfied.

IV.CONSTRUCTING ATTACK MODELS WITH ASDL PROGRAMS

With ASL and ASDL at hands,we can construct a universal formal model for descriptions of some attack behaviors and their communication phenomenon.Section IV-A will gives this model.And this ASDL model will guide us on the road to the case studies in Section IV-B and Section IV-C.

A.Model

The formal description of the new model is given in the Appendix B.Here we only use the various representative examples and their illustrations to depict and portray all of the key features of the new model,as shown in Table III.The illustrations of Tables I and II can also help us understand the intuitive meaning of the new model,by depicting the intuitive meaning of ASL and ASDL.

B.Case Study:Coordinated Password Cracking Attacks

1)The Attack Principle and Our Prolusion:As mentioned in Section I,driver allows many machines in different subnets collaboratively use a unified strategy to launch password guessing.At anytime,at most one machine can be permitted to send its password connection.Thus,the password guessingis greatly accelerated,and the conflicts in the addresses never occur.

TABLE I(INCLUDING CHROMATIC FIGURES)THE ASL FORMULAS AND THEIR INTUITIVE MEANING(WHERE THE CIRCLE IN RED MEANS THE CURRENT STATE)

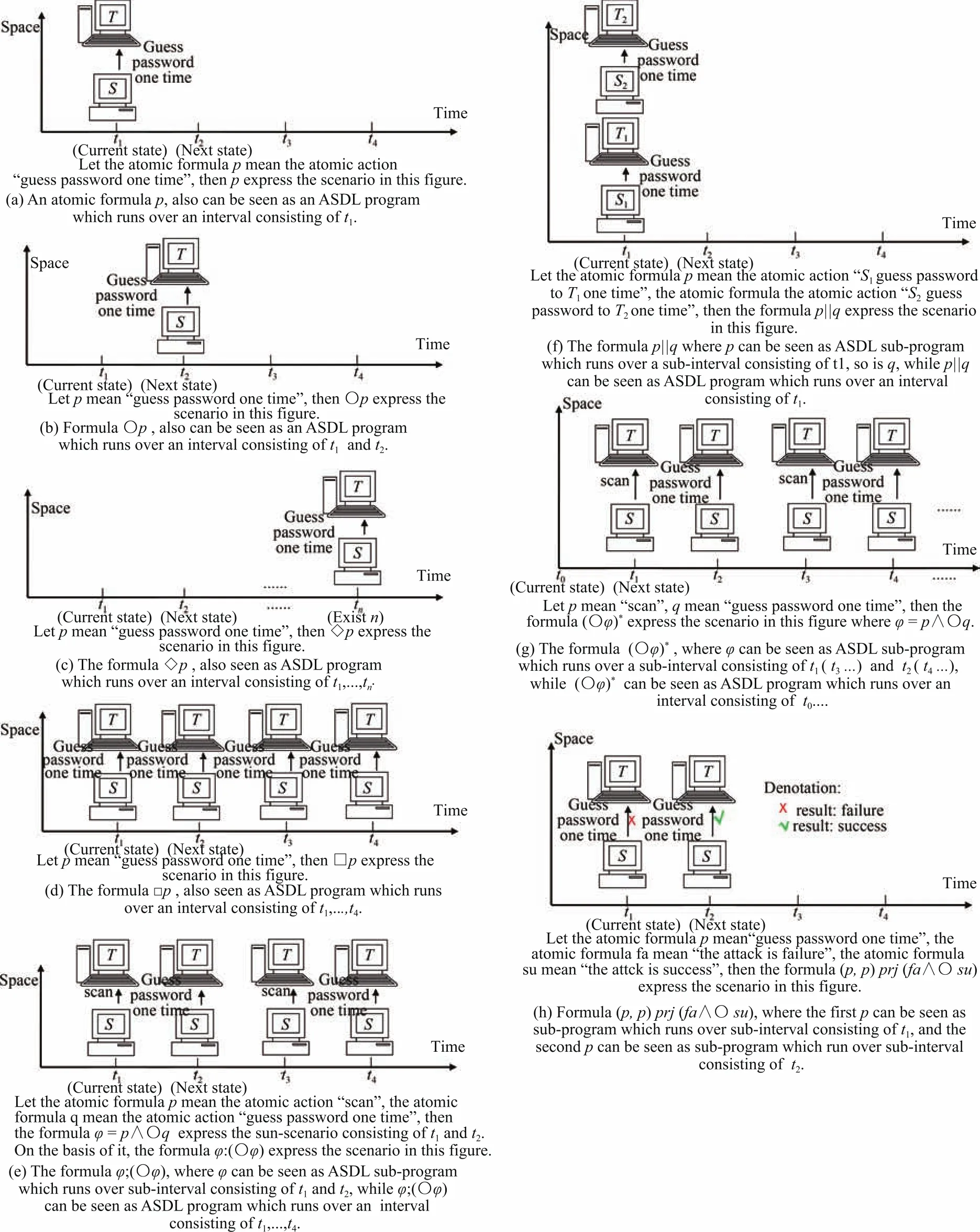
Fig.3.Illustrations of ASL formulas via example from realworld:password guessing.

The driver utilizes multiple source nodes to launch attacks.Steps of an attack from a source node can be formulated as follows.1)an intruder scans the victim machine,it is denoted as an atomic formulaw1;2)the intruder tries to generate a password and connect the victim machine,it is denoted as an atomic formulaw2.

For simplicity,we assume that there are two attack source nodes.Each time,one intruder selects a source node and launches an attack.During the implementation process of the second step launched by one source node,any other process of the second step conducted by another source node is forbidden.That is to say,it does not allow two processes to try a connection to input a password at the same time.We can use two Boolean expressions denoted asb1andb2to synchronizethe processes.Fori=1 ori=2,biis a Boolean expression which indicates whether Step 2)of theith process is being executed or not.

TABLE II(INCLUDING CHROMATIC FIGURES)ASDL STATEMENTS AND THEIR INTUITIVE MEANING(WHERE THE CIRCLE IN RED MEANS THE CURRENT STATE)

2)How to Get an ASDL Program for Expressing Coordinated Password Attacks:Fig.4 illustrates the procedure of getting this ASDL program.In this figure,the upper dotted square limns the process 1,whereas the lower dotted square limns the process 2.First,for each process,the logical relationships,in particular the temporal relationships among the various attack steps and attack actions are depicted,as shown in the circles and the arrows in the figure.Second,for each process,the atomic formulas and the sub-formulas whichare expressing these steps and actions are marked around the circles and the arrows.Last,according to the logical relationships including the temporal relationships among the atomic formulas and the sub-formulas,we get the two programsP1andP2which are expressing the two processes,respectively,as shown in the figure.Since the process 1 and the process 2 are concurrent,P=P1‖P2is the required ASDL program.

TABLE III(INCLUDING CHROMATIC FIGURES)SOME KEY FEATURES OF THE ASDL MODEL(A CIRCLE MEANS A STATE,WHEREAS A SQUARE MEANS A SEQUENCE OF STATES)

It is noticeable that the statementframeis very useful in this case.With this statement at hands,we no longer need to explicitly assign the specific values tob1andb2in each state,since these two variables can inherit the values from their previous states implicitly.As a result,the ASDL program modeling the process 1 can be described asP1=frame(b1)∧¬b1∧while¬successdom ore;ifb2then await(¬b2)elseempty;,and the ASDL program modeling the process2 can be described asP2=frame(b2)∧¬b2∧while¬successdo(w1∧m ore;ifb1then await(¬b1)elseempty;

It is noticeable that the statement“await”ensures that Step 2)of the two processes cannot be executed at the same time.The attacks are repeated until success,it is denoted by the statement“while”.

C.Case Study:Chop-chop Attacks Launched From Multimachines

1)The Attack Principle and Our Prolusion:In order to launch chop-chop attacks on wireless networks,an intruder frequently uses the following way.He or she revises a byte of an encrypting data packet and replays this packet to the access point(AP),while monitoring the AP.Chop-chop attacks can slowly crack the data packets protected by WEP without considering the size of keys.The principle of this type of attack can be summarized follows:

Fig.4.Illustration of getting ASDL program for coordinated password attacks.

At first,an intruder waits for the data to be transmitted.Even if there is no AP connecting some clients,the network also has a few packets.

And then,the intruder selects a byte and deletes this byte from a data packet.The checksum of this packet is recalculated on the assumption that the value of the deleted byte is 0.The modified data packet is sent again to a multicast address in order to check whether the AP will forward this packet or not.

If this packet is forwarded,apparently the recalculated checksum is correct,and so does the value of the guessed clear text.A byte of clear text and a byte of secret-key are cracked in this way.

If this packet is not forwarded,the value of the guessed clear text is not correct,and it will be added by 1.The above steps will be repeated until the correct value is hit(atmost 256 times loops for one byte).

The above procedure for one byte will be repeated until every byte of data packets has been cracked.

For AP,the following steps in each loop of every byte are visible:1)a data packet is sent,it is denoted asw1;2)the packet which has been modified for one byte is received,it is denoted asw2;3)the checksum is recalculated,it is denoted asw3;4)check whether or not the modified version of the packet is forwarded,it is denoted asw4.

Multiple attack processes will produce concurrency on the same target machine if a coordinated attack is launched from many source machines.Under the circumstance,Step 3)in different processes cannot be executed at the same time due to mutual exclusion of local resources.Therefore,Step 3)needs to be synchronized.

2)How to Get an ASDL Program for Expressing Coordinated Chop-chop:Supposing there are two concurrent processes,we can depict the illustrations for these two processes in the same way as the ones in Fig.4,as shown in the two dotted squares of Fig.5,respectively.

With the statement frame at hands,we no longer need to explicitly assign the given values tob1andb2in each state.As a result,we have:

Since the process 1 and the process 2 are concurrent,P=P1‖P2is the required ASDL program.That is to say,a coordinated chop-chop attack originated from double sources can be formulized as an ASDL programP1‖P2.

Fig.5.Illustration of getting ASDL program for coordinated chop-chop attacks.

V.A COMPARISON OF POWER BETWEEN

The question now is how about the expressive ability of ASDL?In order to make it clear,we make a theoretical study,through a formal proof.See Appendix C for more details on the process of the formal proving.

The result indicates that the constructsprj+prjΘhave a more expressive power than the constructschop+chop star.And the result also answers the following questions:what attack behaviors can be expressed by the former constructs rather than by the latter ones?The answer is that the attacks satisfy simultaneously the following two conditions:1)the length of the loop body,i.e.,repeated attack sub-behaviors,is no less than 2,and the length is a variable;2)the number of the execution of the loop is a constant.

This reveals the fact that it is just RASL in[5]and ASDL in this paper rather than LTL employed in[1]and ITL in[2]that can describe the attacks which satisfy the above two conditions due to the different constructs in the different logics.

VI.AN ASDL MODEL CHECKING ALGORITHM AND ITS IDS ALGORITHM

We can get an ASDL model checking algorithm via the formal theorem proving.The process of the theorem proving has been formalized.See Appendix D for more details.On the basis of it,we can detect some network attacks via the ASDL model checking algorithm.

The core of the ASDL-based intrusion detection method is:1)use an ASDL program to describe an attack signature;2)use another ASDL program to describe a record in an audit log;3)the signature and the record constitute the two inputs of the model checking algorithm;4)the output of the model checking algorithm is the result of intrusion detection.

The principle of the ASDL-based intrusion detection algorithm is illustrated by Fig.6.

Fig.6.An intrusion detection algorithm with ASDL.

V II.SIMULATIONS

The LTL-based method in[1],[4],[9],the ITL-based method in[2],the RASL-based method in[5]and the ASDL-based method presented in this paper,all of these approaches are based on the model checking technique.In order to compare the existing approaches with our new algorithm,we conduct some simulations and try to detect some analog password attacks and analog coordinated attacks mentioned above.The platform used is a PC with Dual Core 3.2GHz,8GB,and Windows 7,along with MATLAB 2010.

A.Experiment 1:for Password Cracking Without Time Constraints

At first,we randomly generate 500 analog attacks.In addition,any time constraint in these attacks is prohibited.Each of the attacks consists of no less than one processes,and each of the process only tries to connect just one time.In other words,none of loop actions occurs in any attack.An attack is a coordinated attack if it has more than one process.In order to detect these produced attacks,we employ the four methods mentioned above,respectively.Fig.7 illustrates the experimental results,where the integerndenotes the number of processes,and a value of y means a ratio of the number of attacks found by an existing method to the number of attacks found by the new method.

Fig.7.A comparison for password cracking(one connection per process).

As shown in Fig.7,the ASDL-based method finds more attacks than other methods.Whennis equal to 1,there is only one process in one attack.At this time,it is not a coordinated attack,and no communication is needed.The number of attacks found by the ASDL-based method is approximately equal to the number of attacks found by the RASL-based method.Whennincreases,more processes take part in the attack.As a result,more and more communication actions among these processes are needed.It is ASDL rather than RASL that can describe validly these communications.Thus,the ASDL-based method finds these communication actions,whereas the RASL-based method does not.As a result,the ratio decreases exponentially as the number of processes increases.In other words,the former method is becoming stronger when n increases,compared with the latter method.The same thing happens when we compare the ASDL-based method to the ITL-based one.And the LTL-based method finds nothing because this logic can not describe any password cracking attack.In a word,none of the MC-based methods except for the ASDL-based one finds communication phenomenon in password cracking attacks without time constraints.

And then,we randomly generate 500 analog attacks again.Each of the attacks consists of no less than one processes,and every process tries to connectktimes.In other words,there are some loop actions in every attack.Once again,we employ the methods mentioned above respectively.Fig.8 illustrates the experimental results.

As shown in Fig.8(a),the ASDL-based method finds more attacks than the RASL-based method.Bothnandkhave great influence on the ratio since each of the two integer variables reflects the requirement for increasing or decreasing the total number of communication actions in a password cracking attack without time constraints.It is ASDL rather than RASL that can easily meet this requirement for description.As a result,the ratio decreases exponentially as the communication actions increase.

Fig.8.Another comparison for password cracking(connect k times).

As shown in Fig.8(b),the ASDL-based method finds more attacks than the ITL-based method.However,only one variable i.e.,naffects the ratio.Whenkis no less than 2,a loop statement is needed to describe some loop actions.It is far beyond the expressive ability of ITL.In other words,ITL cannot describe any attack with loop actions.As a result,the ITL-based method finds nothing whenkis larger than 1.

Similar to Fig.7,Fig.8(c)shows that the LTL-based method finds nothing once again since this logic cannot describe any password cracking attack.

In a word,Experiment 1 suggests the following rules for checking the password cracking attacks without time constraints:1)The ASDL-based method can be employed to conveniently detect some communication actions among the processes and loop actions in an attack;2)The RASL-based method can be employed to conveniently detect some loop actions in an attack;3)The ITL-based method can only find trivial actions in an attack;4)Nothing can be found by the LTL-based method.These rules are valid since the different logic can express validly some different actions in an attack.

B.Experiment 2:for Password Cracking With/Without Time Constraints

Now,we random ly generate 500 analog attacks.Moreover,time constraints in these attacks are permitted.That is to say,some of the produced attacks have time constraints.Each of the produced attacks consists of no less than one processes,and every attack tries to connectktimes.In other words,some of them are coordinated attacks.In order to detect these produced attacks,we employ the RASL-based method and our ASDL-based method respectively.Fig.9 illustrates the experimental results.

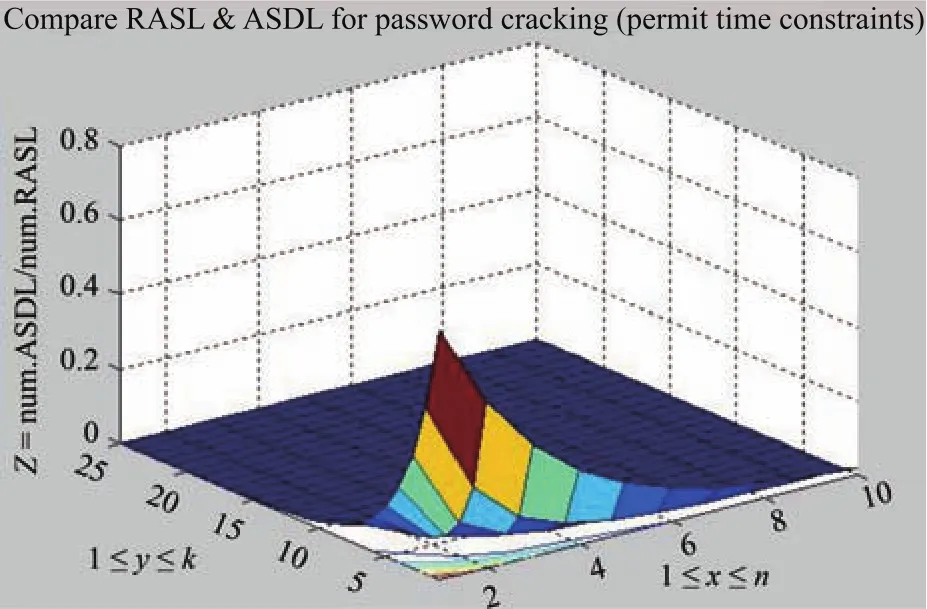
Fig.9.Comparison for password cracking(time constructs).

In contrast to Fig.8(a),this time the RASL-based method finds more attacks than the ASDL-based method,as shown in Fig.9.On the one hand,the latter method finds communication actions in an attack,as mentioned above.On the other hand,it is the former method rather than the latter one that finds time constraints in an attack since only RASL can describe some time constraints.Similar to the ASDL-based method,the ITL-based one and the LTL-based one do not find any time constraint in an attack because none of these logics can express time constraint.

C.Experiment 3:for Chop-chop

Now,it is chop-chop attacks.We random ly generate 500 analog attacks.In addition,any time constraint in these attacks is prohibited.Some of the produced attacks are coordinated ones.In order to detect these produced attacks,we employ the four methods mentioned above respectively.Fig.10 illustrates the experimental results.

Fig.10.Comparison for chop-chop.

Similar to password cracking attacks,more chop-chop attacks are found by the ASDL-based method rather than by other methods.With the increase of the number of processes,the advantage of the new method is more and more obvious.The direct cause of this phenomenon is essentially the same as in the case of password cracking attacks.

D.Some Discussions

Table IV gives the abilities of the four logics for describing some types of attacks.According to the three simulation experiments,we summarize some characteristics of the power of detection with regard to the new algorithm and the existing MC-based approaches,as shown in Table V.According to these two tables,we can infer that the different algorithm has the different power due to the different ability of attack description of the different logic.Compared with LTL,ITL and RASL,ASDL has the ability of convenient description of synchronization communications among concurrent attack processes.This is the reason why the new method can perform better.

V III.CONCLUSIONS

In this paper,we present an ASDL-based intrusion detection method.And some coordinated attacks with synchronization mechanisms are detected in our simulations.As a logical program language,ASDL can be executed directly to detect network attacks(see Table VI).As a result,it offers a much more convenient way to find complex attack behaviors.The LTL-based method is the first IDS which detects successfully chop-chop attacks,as reported in[10].To the best of our know ledge,the new algorithm is the first IDS method for detecting coordinated chop-chop attacks.

TABLE IV A COMPARISON OF DESCRIPTION ABILITIES OF THE DIFFERENT LOGICS FOR SOME TYPES OF ATTACKS(WHETHER THE ACTIONS CAN BE DESCRIBED OR NOT)

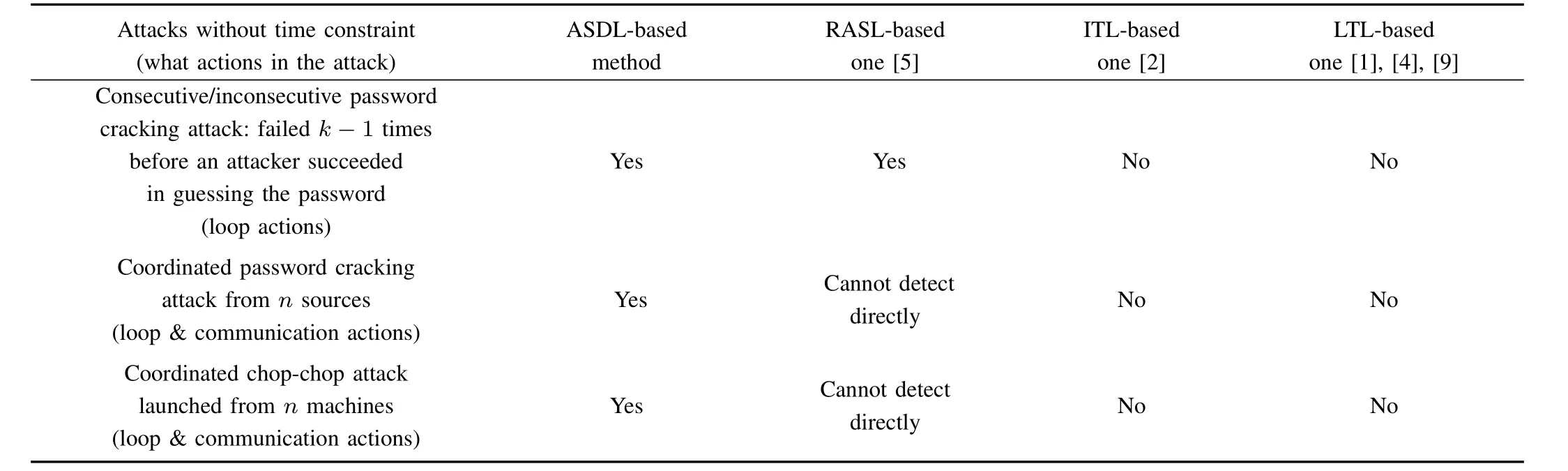
TABLE V A COMPARISON OF POWER AMONG THE MC-BASED IDS ALGORITHMS FOR SOME TYPES OF ATTACKS(WHETHER THE ATTACKS ARE FOUND OR NOT)

TABLE VI A COMPARISON OF THE WAY OF DETECTION BETWEEN THE FOUR ALGORITHMS

APPENDIX A ASL AND ASDL:THE FORMAL DESCRIPTION

A.ASL

The formal definitions of the ASL formulas are as follows.

Definition 1:ASL formulas have the following syntax given in the Backus-Naur form:

Definition 2:A state s is defined on Kripke structure,ands:p→Bwherepis an atomic proposition,andB={true,false}.

Definition 3:An intervalσis a state sequence〈si,...,sj〉,whereand|σ|=j−i.

Definition 4:An interpretation is a quadrupleI=(σ,i,k,j),wherei≤k≤j,andkis the current state.We use the notation(σ,i,k,j)|=ϕto mean that formulaϕis satisfied in the interval〈si,...,sj〉.And we use the notationlen(σ)to mean|σ|.

Definition 5:Letσ=〈s0,s1,...,s|σ|〉be an interval,r1,...,rhbe a series of integers,and 0≤r1≤r2≤···≤rh≤|σ|.We use notationσ↓(r1,...,rh)=〈st1,st2,...,stl〉to denote a projection fromσtor1,...,rh,wheret1,...,tlis obtained by deleting the duplicate numbers fromr1,...,rh.

Definition 6:The satisfaction relation|=is inductively defined as follows:

I−Ap:I|=pif and only ifsk[p]=true,wherep∈ApandApis a set of atomic propositions;

I−not:I|=¬ϕif and only ifI/|=ϕ;

I−or:I|=ϕ1∨ ϕ2if and only ifI|=ϕ1orI|=ϕ2;

I−skip:I|=skipif and only iflen(σ)=1;

I−prj:I|=(ϕ1,...,ϕm)prjΨ if and only if,there exists an integerk=r0≤r1≤···≤rm≤j,and(σ,i,k,r1)|=ϕ1,...,(σ,rn−1,rn−1,rn)|=ϕn,1＜n≤m,forσ′in the following two cases,(σ′,0,0,|σ′|)|= Ψ holds:a)rm＜jandσ′=σ↓(r0,...,rm)·σ(rm+1,...,j),b)rm=jandσ′=σ↓(r0,...,rh),0≤h≤m;

I−prjΘ:I|=(ϕ1,...,(ϕi,...ϕj)Θ,...,ϕm)prjϕ0if and only if there existsn∈N0,such thatI|=(ϕ1,...,(ϕi,...,ϕj)n,...,ϕm)prjϕ0.

TABLE VII FORMAL MODEL:SOME ASDL PROGRAMS AND THEIR ATTACK BEHAVIOR

Definition 7:The derived formulas are defined as follows:

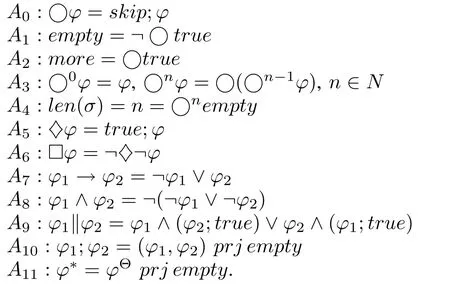
B.ASDL

The formal definitions of the ASDL statements are formalized as follows,wherexis a variable,eis a Boolean expression,bis a Boolean expression,andsis a statement.Furthermore,all ofx,bandeare finite and enumerable.

Definition 8:Letxbe a variable,bbe a Boolean expression,and the number ofbandxis finite and enumerable,we havewhereaf(x)holds if and only ifxis assigned at the current states.

Definition 9:frame(x)=□(more→○lbf(x)).

Definition 10:The basic ASDL statements are defined as follows:

1)Empty statement:empty.

2)Assignment statement:

3)Frame statement:frame(x).

4)Next statement:

5)Projection statement:(s1,...,sm)prj s.

6)Sequence statement:s1;s2≡(s1,s2)prj empty.

7)Disjunctive statement:s1∨s2.

8)Conjunctive statement:s1∧s2.

9)Parallel statement:

10)If statement:ifbthens1else2).

11)While statement:whilebdo).

12)Until statement:repeatsuntilb≡s;whiledos.

13)Await statement:await(b)≡frame(x1,...,xh)∧□(empty↔b),wherex1,...,xhis the variables ofb.

14)Projection star statement:(s1,...,(si,...,sj)Θ,...,sm)prj s.

APPENDIX B THE ASDL MODEL:THE FORMAL DESCRIPTION

The complete formal description of the ASDL model for expressing attack behaviors is shown in Table VII.

APPENDIX C FORMAL PROV ING:A COMPARISON BETWEEN

In brief,the following theorems tell us what the statements in ASDL rather than the statements in other temporal logic program languages can do,with the help of Figs.11−13.

Theorem 1:Let Ψ andϕbe the two interval formulas,whereandn∈Nis a variable.Supposingϕ= Ψ;...;Ψ,and Ψ is circulatedktimes,wherek∈Nis a constant,we have:1)ϕcan be replaced by a formula which just containsprjand Θ rather than;and*.2)ϕcannot be replaced by a formula which just contains;and*rather thanprjand Θ.

Proof:1)At first,we can construct a formulaϕ=((ΨΘ,b)prj(((true∧skip)∗∧len(k+1));c))∧□(b↔c).According toA11in Definition 7,we haveϕ=((ΨΘ,b)prj((((true∧skip)Θprj empty)∧len(k+1));c))∧□(b↔c).According toA10in Definition 7,we obtain the following formulaϕ=((ΨΘ,b)prj(((((true∧skip)Θprj empty)∧len(k+1));c)prj empty))Thus,prjand Θ instead of;and*occur in the formula.

TABLE VIII SOME NOTATIONS OCCURRED IN TABLE VII AND THEIR MEANS

Fig.11. Three cases on different length of projection.

Fig.12. ϕ =((ΨΘ,b)prj(((true∧skip)∗∧len(k+1));c))∧□(b↔c),where k=3.

And then,we will answer the question why does the formulaϕ=((ΨΘ,b)prj(((true∧skip)∗∧len(k+1));c))formalizes the preconditions or premises.The reasons are formulated as follows.According to the definition ofprj,for any stateholds,we can infer that the intervalΨΘand the interval(true∧skip)∗terminate in the same state.Sincelen(k+1)indicates that the sub-interval(true∧skip)circulates(k+1)times,we can infer that the sub-interval Ψ circulatedktimes according to the definition ofprj,as illustrated in Fig.12.

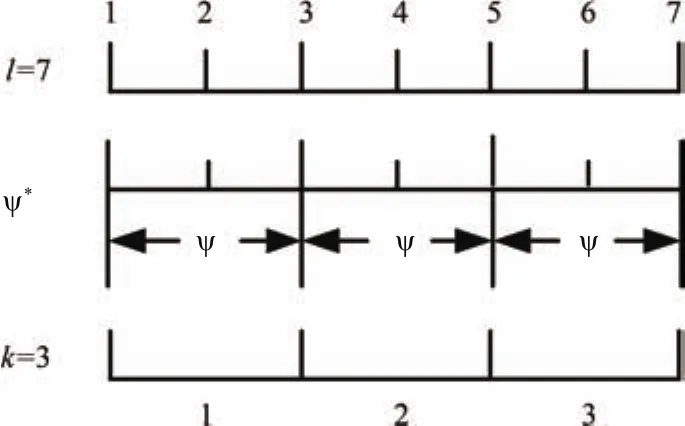
Fig.13. If Ψ is circulated three times,i.e.,k=3,and|σΨ|=a=3,|σΨ∗|=l=(a−1)×k+1=(3−1)×3+1=7.

2)Proof by contradiction is employed.Let us supposeϕcan expressed by a formula which just contains;and*rather thanprjand Θ.Only the constructlen(l),i.e.,,can define a given length for a sub-interval in which time elapses,due to the definition of the logic.Letϕ=···len(l)···,andl=khold.In order to control the number of the cycle of Ψ in Ψ∗,we just have the two following ways to allocate the position oflen(l)and*.a)len(l)is present in the scope of*,i.e.,(len(l)∧Ψ)∗.In this case,holds.b)len(l)is not present in the scope of*,i.e.,len(l)∧Ψ∗.In this case,where Ψ circulatesmtimes.We cannot obtain the value ofm,because the number of cycles,denoted asm,are relevant ton.Under this circumstance,l/=kholds,even ifm=k.Thus,we havel/=k,regardless of a)or b)And it leads to a contradiction since we have supposedl=k.Therefore,the property 2)holds.

Theorem 2:Let Ψ andϕbe the two interval formulas,whereanda∈Nis a constant.Supposingϕ= Ψ,...,Ψ,and Ψ circulatesktimes,wherek∈Nis a constant,we haveϕ=Ψ∗∧len(a·k−k+1).

Proof:According to b)in the proof of Theorem 1,we construct a formula denoted as.As shown in Fig.13,holds.Thus,l=a·k−k+1 holds ifm=k.Therefore,ϕ= Ψ∗∧len(l)= Ψ∗∧len(a·k−k+1)holds.

The following examples show more clearly what we can do with the statements in ASDL rather than the statements in other temporal logic program languages.

Example 1:Formulmeans thatrepeats one thousand times.

Example 2:The following formulaϕmeans thatΨ=circulates one thousand times:ϕlen(1001));c))∧□(b↔c).Andϕcannot be replaced by anyPITL∗formula.The reasons are formulated as follows.We are unable to determine the value of the variablelin the formulasuch that*just repeats one thousand times.And the value ofl=|σΨ∗|cannot be determined because the length of sub-interval Ψ cannot be determined.

APPENDIX D FORMAL PROOF:AN ASDL MODEL CHECK ING ALGORITHM

In fact,the proofs of Theorems5 and 6 will give the formal description of the ASDL model checking algorithm.

Lemma 1[5]:Any RASL formula is decidable.

Theorem 2:Any ASL formula is decidable.

Proof:ASL is decidable if RASL is decidable since the former logic is a subset of the latter logic.According to Lemma 1,we have a ASL formula is decidable.

Lemma 3:Supposing that the numbers ofbandxare finite and enumerable,we haveis decidable.

Proof:Letb1,...,bnbe all of the values of Boolean expressionb.Using a new atomic propositionpxto denoteaf(x),we haveLet the atomic propositionsq1,...,qndenotex=b1,...,x=bn,respectively.Thus,we have.It is quite evident thatis an ASL formula.According to Theorem 2,we haveis decidable.

Lemma 4:Supposing that the number ofxis finite and enumerable,we haveframe(x)is decidable.

Proof:frameIt is quite evident thatframe(x)is an ASL formula.According to Theorem 2,we haveframe(x)is decidable.

Theorem 5:Any ASDL programPis decidable.

Proof:The proof proceeds by induction on the structure of ASDL programs.

Base:

IfP≡empty,it is quite evident thatemptyis an ASL formula.According to Theorem 2,we havePis decidable.

Induction:

SupposeP≡s1orP≡s2orP≡sm,wheres1,...smare ASDL programs.Then,

1)IfP≡skip∧○x=e,it is quite evident thatskip∧○x=eis an ASL formula sinceeis finite and enumerable.According to Theorem 2,we havePis decidable.

2)IfP≡frame(x),according to Lemma 4,we havePis decidable.

3)IfP≡○s,it is quite evident that○sis an ASL formula.According to Theorem 2,we havePis decidable.

4)IfP≡(s1,...,sm)prj s,it is quite evident that(s1,...,sm)prj sis an ASL formula.According to Theorem 2,we havePis decidable.

5)IfP≡s1;s2≡(s1,s2)prj empty,it is quite evident that(s1,s2)prj emptyis an ASL formula.According to Theorem 2,we havePis decidable.

6)IfP≡s1∨s2,it is quite evident thats1∨s2is an ASL formula.According to Theorem 2,we havePis decidable.

7)IfP≡s1∧s2,it is quite evident thats1∧s2is an ASL formula.According to Theorem 2,we havePis decidable.

8)IfP≡s1‖s2≡s1∧(s2;true)∨s2∧(s1;true),it is quite evident thats1∧(s2;true)∨s2∧(s1;true)is an ASL formula.According to Theorem 2,we havePis decidable.

9)IfP≡ifbthens1elses2≡(b→s1)∧(¬b→s2),it is quite evident that(b→s1)∧(¬b→s2)is an ASL formula sincebis finite and enumerable.According to Theorem 2,we havePis decidable.

10)IfP≡whilebdos≡(b∧s)∗∧□(empty→¬b),it is quite evident that(b∧s)∗∧□(empty→¬b)is an ASL formula sincebis finite and enumerable.According to Theorem 2,we havePis decidable.

11)If repeatsuntilb≡s;while¬bdos≡s;((¬b∧s)∗ ∧□(empty→b)),it is quite evident thats;((¬b∧s)∗∧□(empty→b))is an ASL formula sincebis finite and enumerable.According to Theorem 2,we havePis decidable.

12)If await(b)≡frame(x1,...,xh)∧□(empty↔b),it is quite evident thatframe(x1,...,xh)∧□(empty↔b)is an ASL formula sincex1,...,xhandbare finite and enumerable.According to Theorem 2 and Lemma 4,we havePis decidable.

13)IfP≡(s1,...,(si,...,sj)Θ,...,sm)prj s,it is quite evident that(s1,...,(si,...,sj)Θ,...,sm)prjsis an ASL formula.According to Theorem 2,we havePis decidable.

Thus:

Any ASDL programPis decidable.

We can express a property by an ASDL program which can be considered as an ASL formula.Furthermore,we can model a system using another ASDL program.Thus,the problem whether or not the system satisfies the property becomes a model checking problem.

Theorem 6:The ASDL model checking problem is decidable.

Proof:Let ASDL programPbe a model of a system,and another ASDL programϕbe a property.Clearly,Pandϕcan be considered as the ASL formulas.We rewrite the model checking problem in order to decide whether or not the following formula is a tautology:P|=ϕ.That is to say,we have to check whether or notP∧¬ϕis unsatisfiable.According to Theorem 5,we haveP∧¬ϕis decidable.The model checking will return“NO”ifP∧¬ϕis unsatisfiable.

[1]M.Roger and J.Goubault-Larrecq,“Log auditing through model checking,”inProc.14th IEEE Workshop on Computer Security Foundations,Washington,DC,USA,2001,pp.220−234.

[2]W.J.Zhu,Z.Y.Wang,and H.B.Zhang,“Intrusion detection algorithm based on model checking interval temporal logic,”China Commun.,vol.8,no.3,pp.66−72,May2011.

[3]E.M.Clarke,O.Grumberg,and D.Peled,Model Checking.Cambridge,Massachusetts,London,England:The M IT Press,1999.

[4]J.Olivain and J.Goubault-Larrecq,“The ORCHIDS intrusion detection tool,”inProc.17th Int.Conf.Computer Aided Verification,Edinburgh,Scotland,UK,2005,pp.286−290.

[5]W.J.Zhu,Q.L.Zhou,W.D.Yang,and H.B.Zhang,“A novel algorithm for intrusion detection based on RASL model checking,”Math.Probl.Eng.,vol.2013,pp.Article ID 621203,Feb.2013.

[6]E.Nowicka and M.Zawada,“Modeling temporal properties of multievent attack signatures in interval temporal logic,”[Online].Available:http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.100.488&rep=rep1&type=pdf.2006.

[7]C.V.Zhou,C.Leckie,and S.Karunasekera,“A survey of coordinated attacks and collaborative intrusion detection,”Comput.Secur.,vol.29,no.1,pp.124−140,Feb.2010.

[8]F.B.Cohen,“A noteon distributed coordinated attacks,”Comput.Secur.,vol.15,no.2,pp.103−121,Dec.1996.

[9]J.Goubault-Larrecq and J.Olivain, “A smell of orchids,”inProc.8th Int.Workshop,RV 2008,Budapest,Hungary,2008,pp.1−20.

[10]R.Ben Younes,G.Tremblay,and G.Bégin,“Extending orchids for intrusion detection in 802.11 wireless networks,”inProc.8th Int.Conf.New Technologies in Distributed Systems,New York,NY,USA,2008,pp.Article ID 8.

[11]Y.Zhang,J.M.Fu,and X.M.Sun,“A method of intrusion detection based onmodel-checking,”J.Wuhan Univ.Nat.Sci.Ed.,vol.51,no.3,pp.319−322,Jun.2005.

[12]M.Q.Ali and E.A -Shaer,“Probabilistic model checking for AMI intrusion detection,”inProc.2013 IEEE Int.Conf.Smart Grid Communications(SmartGridComm),Vancouver,BC,Canada,2013,pp.468−473.

[13]A.M.Ahmed,“Online network intrusion detection system using temporal logic and stream data processing,”Ph.D.dissertation,Univ.of Liverpool,Liverpool,UK,2013.

[14]T.Jacob,M.Raman,and S.Singh,“Intrusion detection in zero know ledge system using model checking approach,”inComputer Networks&Communications(NetCom),N.Chaki,N.Meghanathan,and D.Nagamalai,Eds.New York,NY,USA:Springer,2013,pp.453−465.

[15]A.Sinha,A.Ry,and S.Singh,“Modeling&verification of sliding window protocol with data loss and intruder detection using NuSMV,”inProc.2nd Int.Conf.Computational Science,Engineering and Information Technology,Coimbatore,India,2012,pp.352−357.

[16]B.Moszkowski, “Reasoning about digital circuits,”Ph.D.dissertation,Depart.Comput.Sci.,Stanford Univ.,Stanford,USA,1983.

[17]Z.H.Duan,Modeling and Analysis of Hybrid Systems.Beijing,China:Science Press,2004.

[18]W.J.Zhu,H.B.Zhang,and Q.L.Zhou,“On the decidability of satisfiability of discrete TITL formulae,”Acta Electron.Sinica,vol.38,no.5,pp.1039−1045,May2010.

[19]C.C.Zhou,C.A.R.Hoare,and A.P.Ravn,“A calculus of durations,”Inf.Process.Lett.,vol.40,no.5,pp.269−276,Dec.1991.

[20]M.G.Ouyang,F.Pan,and Y.T.Zhang,“ISITL:Intrusion signatures in augmented interval temporal logic,”inProc.Int.Conf.Machine Learning and Cybernetics,Xi’an,China,vol.3,pp.1630−1635,2003.

[21]M.G.Ouyang and Y.B.Zhou,“ISDTM:An intrusion signatures description temporal model,”Wuhan Univ.J.Nat.Sci.,vol.8,no.2,pp.373−378,Jun.2003.

[22]P.Beaucamps,I.Gnaedig,and J.Y.Marion,“Abstraction-based malware analysis using rewriting and model checking,”inProc.17th European Symp.Research in Computer Security,Pisa,Italy,2012,pp.806−823.

[23]J.Kinder,S.Katzenbeisser,C.Schallhart,and H.Veith,“Proactive detection of computer worms using model checking,”IEEE Trans.Depend.Secure Comput.,vol.7,no.4,pp.424−438,Oct.−Dec.2010.

[24]F.Song and T.Touili, “LTL model-checking for malware detection,”inProc.19th Int.Conf.Tools and Algorithms for the Construction and Analysis of Systems,Rome,Italy,2013,pp.416−431.

[25]F.Song and T.Touili,“Efficient malware detection using modelchecking,”inProc.18th Int.Symp.Formal Methods,Paris,France,2012,pp.418−433.

[26]F.Song and T.Touili,“Model-checking for android malware detection,”inProc.12th Asian Symp.Programming Languages and Systems,Singapore,2014,pp.216−235.

[27]F.Song and T.Touili,“Pushdown model checking formalware detection,”Int.J.Softw.Tools Technol.Transf.,vol.16,no.2,pp.147−173,Apr.2014.

[28]S.Schmerl,M.Vogel,and H.König,“Usingmodel checking to identify errors in intrusion detection signatures,”Int.J.Softw.Tools Technol.Transf.,vol.13,no.1,pp.89−106,Jan.2011.

[29]Y.Sun,T.Y.Wu,X.Q.Ma,and H.C.Chao,“Modeling and verifying EPC network intrusion system based on timed automata,”Perv.Mobile Comput.,vol.24,pp.61−76,Dec.2015.

[30]N.Ellouze,S.Rekhis,M.A llouche,and N.Boudriga,“Digital investigation of security attacks on cardiac implantable medical devices,”Electron.Proc.Theor.Comput.Sci.,vol.165,pp.15−30,Oct.2014.

[31]Z.H.Duan,C.Tian,and L.Zhang,“A decision procedure for propositional projection temporal logic with infinite models,”Acta Inf.,vol.45,no.1,pp.43−78,Feb.2008.

[32]C.Tian and Z.H.Duan,“Complexity of propositional projection temporal logic with star,”Math.Struct.Comput.Sci.,vol.19,no.1,pp.73−100,Feb.2009.

[33]C.Tian and Z.H.Duan,“Expressiveness of propositional projection temporal logic with star,”Theor.Comput.Sci.,vol.412,no.18,pp.1729−1744,Apr.2011.

[34]Z.H.Duan,Temporal Logic and Temporal Logic Programming.Beijing:Science Press,2005.

[35]X.B.Wang,“Object-oriented MSVL and its application to verification of composite web services,”Ph.D.dissertation,Univ.of Xidian,Xi’an,China,2009.