Data Gathering in Wireless Sensor Networks Via Regular Low Density Parity Check Matrix

Xiaoxia Song and Yong Li

I.INTRODUCTION

SINCE wireless sensor networks(WSNs)can change the interaction mode between the human being and the world,it has been deployed in a wide range of applications scenarios,such as military,environmental monitoring,physiological monitoring,transportation and agriculture[1]−[3].However,there are two main challenges in the development of WSNs.One is that it will face the impact of big data[4],whose research is still in its infancy.The other challenge is energy consumption problem of sensor nodes since each sensor node is usually powered by batteries which cannot be recharged in many cases[5].It is an important way to reduce energy consumption via data gathering in WSNs[6].The articles[5],[7],[8]utilize data gathering methods based on chain,hierarchy,and tree structures.In[9],a prediction-based data collection method using Kalman filter is provided.Clusterbased data gathering methods are used in[10],[11].However,these methods usually result in the early death of some sensor nodes since they are frequently used and consume more energy than others.So these methods have the drawback of unbalanced energy consumption,which will shorten the lifetime of the network inevitably.This paper considers the energy consumption problem from the aspect of data gathering based on sensing matrix.

It is well known that data gathering methods based on random sensing can reduce energy consumption of sensor nodes since they can capture the feature of ak-sparse signal by a small number of measurements[5],[12].The present study shows that random matrices,such as the Gaussian and Bernoulli matrices,satisfy restricted isometry property(RIP)with high probability and achieve the guaranteed reconstruction performance[13],[14].However,the randomness and density of those matrices usually result in the following problems.1)Random sensing matrices cannot be utilized in some situations where the samplers must be the deterministic matrices and their implementations are usually difficult[15].2)The density will lead to high computation complexity,large storage spaces and more sensors or detectors in practical settings[16],[17].

To solve problem 1),some deterministic matrices,such as chirp sensing matrices[18],BCH sensing matrices[19],and Toeplitz sensing matrices[20],have been proposed.Although RIP is an acknowledged performance metric,there is no algorithm to check whether a deterministic matrix satisfies RIP or not.So some other performance metrics,such as the mutual coherence[14],statistical restricted isometry property(StRIP)[21]andk-set correlation[22],are provided to measure the performance of sensing matrix.To solve problem 2),sparse sensing matrices are constructed respectively by adjacency matrices of a high-quality unbalanced expander graph and an optimized family of expander graphs in[16],[23].Reference[24]develops a sparse encoder matrix like low density parity check(LDPC)matrix and a belief propagation decoder under the Bayesian framework.Although it can accelerate encoding and decoding,it does not guarantee the performance of sensing matrix by the acknowledged metrics.

In this paper,we construct a class of deterministic sparse sensing matrices having small mutual coherence and satisfying StRIP via regular LDPC(RLDPC)matrices,and propose a data gathering method based on RLDPC sensing matrix.Firstly,we deduce that the mutual coherence of RLDPC matrix has the order ofO(1/ωc)in Proposition 2,whereωcis column weights of the matrix.And then the condition that RLDPC matrix satisfying StRIP is provided in Propositions 3 and 4 by introducing the relationship between StRIP and the mutual coherence.According to Propositions 2−4,the sensing matrix is constructed by con fining the column weights or sparsity level of RLDPC matrix and eliminating short loops of the corresponding tanner graph of the measure(the details of tanner graph can be referred to Section II-B).So the constructed sensing matrix has small mutual coherence and satisfies StRIP.In general,more measurements are needed to reconstruct the signal by deterministic sparse sensing matrix compared to random dense sensing matrix[24],[25].However,since the constructed sensing matrix obeys a special rule discussed in[25],it has the same scale of measurement numbers as the dense measurement ensembles for signal recovery,whose proof is given in Proposition 5 of Section III.Experimental results verify that the constructed sensing matrices have better reconstruction performance,compared to the Gaussian,Bernoulli,and CS-LDPC[24]matrices.And they also show that the data gathering based on RLDPC matrices can reduce energy consumption of sensor nodes compared with those via other three sensing matrices on the premise of the same reconstruction performance.

This paper has the following three contributions.Firstly,we construct a class of deterministic sparse sensing matrices with performance guarantee,which is important and difficult issue in the construction of sensing matrix area.Secondly,we prove that the constructed sensing matrix has the same scale of measurement numbers as the dense measurements.Thirdly,we propose a data gathering method via the constructed RLDPC matrix,which can reduce energy consumption compared to the data gathering methods via the random matrix and has higher reconstruction performance than the existing data gathering method via the other sparse matrices.In addition,the proposed data gathering method is suitable for the situations with strong temporal and spatial correlation in WSNs.It corresponds to the cases that the acquired data have sparse feature.

This paper is organized as follows.Section II illustrates the preliminaries of sensing matrix.Section III introduces the detailed algorithm and analyses the performance of RLDPC sensing matrix.Section IV proposes a data gathering method based on the constructed RLDPC sensing matrix.Section V shows the experimental results.The conclusions are given in Section VI.

II.PRELIMINARIES OF SENSING MATRICES

In this section,we firstly introduce some metrics to measure the performance of sensing matrix.Then,we illustrate the tanner graph of the measure.Finally we describe a class of sparse matrices called RLDPC matrix.

A.The Performance Metrics of Sensing Matrix

RIP,proposed by Candes and Tao[26],is the first and the most famous performance metric of sensing matrix.If a sensing matrix Φ,whose column vectors have unit norms,satisfies

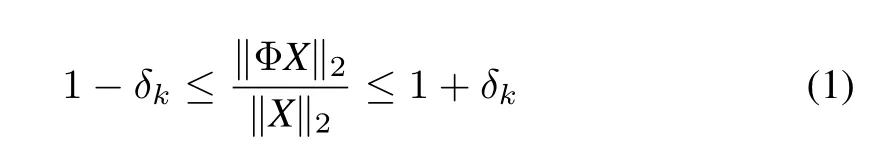
for allk-sparse vectorsXwith restricted isometry constantδk,then Φ is said to obey RIP of orderk(k-RIP).The condition that Φ satisfies 2k-RIP is sufficient to perfectly reconstructksparse vectors from a small number of measurements.Since random matrices,such as the Gaussian and Bernoulli matrices with independent and identical distribution,satisfy 2k-RIP with high probability,they are commonly used as sensing matrices in the compressed sensing framework.

However,there is no algorithm to check whether a given matrix satisfies RIP or not.So some relaxed performance metrics are proposed.StRIP[21]is a new performance metric to measure the sensing matrix.If anM×Nsensing matrix Φ satisfies

with probability exceeding 1−δ,then Φ is said to obey(2k,ε,δ)-StRIP.If Φ satisfies(2k,ε,δ)-StRIP,thenk-sparse vectors can be perfectly reconstructed from a small number of measurements with high probability.Obviously,StRIP is a weaker version of RIP.In addition,there are some other performance metrics like the mutual coherence[14]andk-set correlation[22],whose details refer to the related references.

B.The Tanner Graph of the Measure

When a random sensing matrix Φ is used to measure anN-length signalX,then compressive measurements can be obtained by

whereandThen,we have

The tanner graph of the above measure can be vividly illustrated in Fig.1.

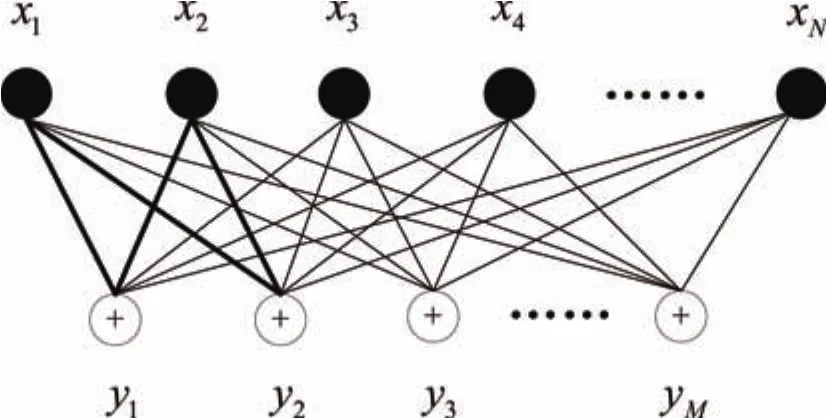
Fig.1.Tanner graph of the measure.

In Fig.1,when Φ is the Gaussian or Bernoulli matrix,there is always an edge betweenyiandxj.It will lead to the result that there always exists a short loop with the length 4 betweenyi1andyi2(1≤i1,i2≤M,i1/=i2),for example,the loop marked in bold linesx1→y1→x2→y2→x1.Such short loops will result in the coherence of the two measurements.So it is possible to reduce the coherence of compressive measurements by decreasing the number of the edges and short loops in the tanner graph.Actually,the number of the edges of tanner graph is right equal to the number of non-zero elements of the sensing matrix.So the coherence of compressive measurements may be reduced by sparse sensing matrix whose tanner graph contains a few edges and short loops.

C.RLDPC Matrix

LDPC matrix is the check matrix of LDPC code.RLDPC matrix is a class of sparse matrices with the following four properties[27],[28].1)Each row consists ofωrelements with the value 1,whereωris called as row weights.2)Each column consists ofωcelements with the value 1,whereωcis called as column weights.3)The number of the element 1 at the same row among any two columns,denoted byλ,is no more than one.4)ωrandωcare less than the length of the code and the row number of the matrix.

LDPC code is the closest to the Shannon limit and its dual code is called as low density generator matrix(LDGM),which is a good compression code[29],so LDPC matrix may be a good sensing matrix.In[24],sparse sensing matrix like LDPC matrix is constructed.Since it satisfies all the above properties 1),2)and 4)except 3),it is not RLDPC matrix.Nevertheless,the property 3)is closely related to the mutual coherence of the sensing matrix.Inspired by it,we construct RLDPC matrix with small mutual coherence in the next section.

III.THE CONSTRUCTION OF RLDPC MATRIX

RLDPC matrix is able to acquire the information uniformly due to its regularity,and has small mutual coherence because of its property 3).Both features are desired in the construction of the sensing matrix.So we construct a class of deterministic sparse sensing matrices via RLDPC matrix.

A.Theoretical Support of the Construction

The StRIP property in[21]provides a metric to measure the performance of deterministic sensing matrix.When a given matrix satisfies StRIP property,the signal can be perfectly reconstructed by a small number of measurements with the overwhelming probability.By analyzing StRIP property,[30]deduces a relationship between StRIP and the mutual coherence,which is described in Proposition 1.

Similarly,we can compute the order of the mutual coherence of RLDPC matrix,which is illustrated in Proposition 2.

Proposition 2:The mutual coherence of RLDPC matrix Φ has the order ofO(1/ωc).

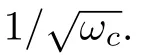
whereAlandAmare any two columns of the matrixA(l/=m),we can deduce

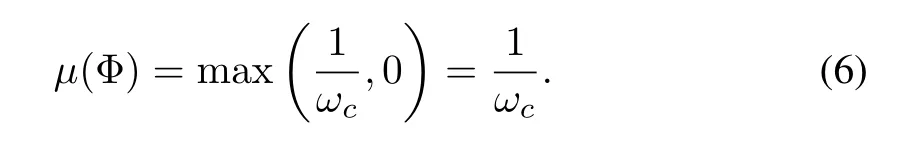
So the mutual coherence of RLDPC matrix Φ has the order ofO(1/ωc).

Based on Propositions 1 and 2,we have a condition that RLDPC matrix satisfies StRIP property,and it is described in Proposition 3.

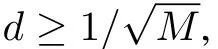
Proof:The sparsity leveldcan be expressed as

In Proposition 3,the relationship between RLDPC matrix Φ with StRIP property and column weightsωcis built.And then we build the relationship between RLDPC matrix Φ with StRIP property and the sparsity level of Φ in Proposition 4.These conclusions can be used to construct sensing matrix via RLDPC matrix.

B.Construction Algorithm of the RLDPC Matrix

In Algorithm 1,we firstly input row numbersMand column numbersNof the constructed sensing matrix,and the column weightωc.In 1),compute the maximal number of 1 allowed in each row denoted byNr,generate an initial matrixaccording to the constraint ofωc,then countc=[c(1)c(2)···c(M)],where is the number of 1 in theith row,and set the row indexi=1,the index of the iteration timesloop=1,and the total iteration timesrloop=R.In 2),ifc(i)＞Nr,then(c(i)−Nr)elements with the value 1 in theith row are moved to other rows withc(i′)＜Nr(1≤i′≤M,i′/=i).In 3),seti=i+1 and repeat 2)and 3)to adjust the row weights of the next row untili＞M.In 4),ifloop≤rloop,setr=1 and go to 5)to eliminate short loops;otherwise go to 7)to stop the computations and output Φ.In 5),search the positions of the elements with the value 1 in therth row,denoted byp,and compute the length ofp,denoted byL.For each rowiexceptr(1≤i≤r−1,r+1≤i≤M),search the short loop(formed by therth andith rows)with the length 4,and eliminate it.Then setr=r+1 and repeat 5)to eliminate the short loops related to therth row untilr＞M.In 6),setrloop=rloop+1 and repeat 4)−6)to continue eliminating the short loops remained in the tanner graph untilloop＞rloop.In 7),output anM×Ndeterministic and sparse RLDPC matrix Φ.In Algorithm 1,steps 2)and 3)constructed the matrix Φ with the same column weightsωcand the almost same row weightsωr.Namely,each column of Φ containsωcelements with the value 1 andM− ωcelements with the value 0,and its each row containsωrelements with the value 1 andM− ωrelements with the value 0.The next steps 4)−6)will eliminate short loops with the length 4 in the tanner graph of the above construction.Next,we will analyze the performance of the constructed deterministic sparse RLDPC matrix in the next subsection.

Algorithm 1.___Algorithm of constructing RLDPC sensing matr_ix

Input.M,N,ωc

Output.Φ

1)Initialize.ComputeNr,generate ΦM×Nsatisfyingωc,computec;seti=1,rloop=Randloop=1.

2)Adjust.Ifc(i)＞Nr,then move(c(i)−Nr)elements with the value 1 from theith row to other rows whose number of 1 is less thanNr.

3)Iterate_1.Seti=i+1 and repeat 2)−3)untili＞M.

4)Judge.Ifloop≤rloop,setr=1,go to 5);Otherwise go to 7).

5)Eliminate.Computep=find(Φ(r)==1)andL=length(p).For each rowi(1≤i≤r,r+1≤i≤M),search the short loops with the length 4,and eliminate.Setr=r+1 and repeat 5)untilr＞M.

6)Iterate_2.Setloop=loop+1 and repeat 4)−6)untilloop＞rloop.

7)Output.______________________________________________

C.Performance Analyses of the Constructed RLDPC Matrix

In this subsection,we will analyze the performance of the constructed RLDPC matrix from two aspects including StRIP property and the scale of measurement numbers.

Although dense measurement ensembles like the Gaussian measurements can obtain the optimal scaling of measurement numbers,it will lead to high computational complexity and huge storage spaces.Sparse measurement ensembles can reduce the costs of computation and storage.Intuitively,sparse measurements should need more measurement numbers to reconstruct the signal than those of dense measurements.Fortunately,[25]gives information-theoretic limits on sparse signal recovery of dense and sparse sensing matrices,and draws the following conclusion for a special case.When,ifthenO(Ms)=O(Md),whereO(Ms)andO(Md)respectively represent the order of measurement numbers of sparse,dense measurement ensembles for signal recovery.

Based on the above conclusion,we give Proposition 5 to illustrate the order of measurement numbers of the constructed sparse sensing matrix.

Proposition 5:SupposeO(Mφ)is the order of the constructed sparse sensing matrix,we haveO(Mφ)=O(Md).

Proof:In our construction,d=ωc/Mandk=βN,whereβis the sparsity level of the underlying signal.So we have

Since 0＜ ωc/M,β＜1,whenN→∞,thendk→ ∞.According to the above conclusion,we can deduce

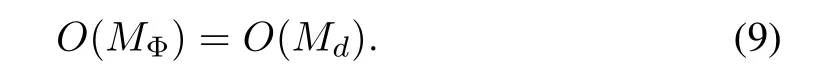
Namely,the constructed sparse sensing matrix has the same scale of measurement numbers as the dense measurement ensembles for signal recovery.

IV.THE PROPOSED DATA GATHERING METHOD BASED ON THE CONSTRUCTED RLDPC MATRIX

A.The Data Gathering Model Based on Sensing Matrix

It is obvious that the vectorYis the low-dimensional measurement,whileXis the high-dimensional signal.The data gathering problem can be considered as data extraction problem whose model is given in(10),i.e.,the signalXis extracted fromY.

However,it is an ill-posed problem due toM＜N.Fortunately,since the signalXin WSNs has the correlations,it has sparse feature.So we can utilize the sparsity of the signal to solve the above ill-posed problem.IfXis compressible,it can be projected to its certain sparse domain Ψ,thenyj=ΦjΨθ,where the coefficientθis sparse,the model illustrated by(10)can be represented as

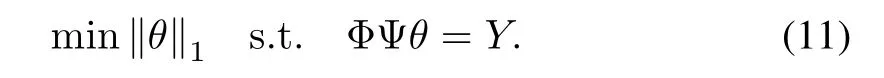
Therefore,we can obtain the data of sensor nodes by solving the optimization problem(10)or(11).

B.The Proposed Data Gathering Method Based on RLDPC

Algorithm 2._Data gathering algorithm based on RLDPC matrix

1)InitializeM,N,d,and generate anM×NRLDPC sensing matrix Φ,and letj=1,i=1,andY=0.

2)ifj≤M,letD=Φiand markD=[d1,d2,...,dN];otherwise go to 6).

3)ifdi=1,thenyi=yj+dixi;otherwise go to 4).

4)Leti=i+1,ifi≤N,then repeat 3)and 4);otherwise go to 5).

5)Letj=j+1,repeat 2)−5).

6)Stop the collection and extractXfromYby using the model__(10)or(11).

V.EXPERIMENT RESULTS

In this section,we firstly compare the reconstruction performance of the constructed sensing matrices with the Gaussian,Bernoulli and CS-LDPC[24]sensing matrices for the measurements with and without noise in Section V.A.In Section V.B,we provide reconstruction performance of the constructed sensing matrices with different sparsity.Then,we show that the data gathering method based on the constructed sensing matrices can reduce the communication energy consumption compared with the methods based on the above mentioned sensing matrices in Section V.C.Homotopy method is selected as the reconstruction algorithm because it is suitable to the recovery of sparse signals[31],[32].

A.The Reconstructions From Measurements Without and With the Noise

In the experiments,random sparse signals are selected as test signals since the data of sensor nodes in WSNs have the sparse feature.Concretely,ak-sparsity signal ofN-length is generated as follows:knon-zero locations are randomly generated and the correspondingkelements are assigned into random numbers between 0 and 1,and the other elements ofN−klocations are set 0.Fig.2 gives an example of random sparse signal withN=200 andk=10.Next,we compare the reconstruction performance of the constructed sensing matrices with the Gaussian,Bernoulli,and CS-LDPC sensing matrices for the measurements with and without noise.And we also test the reconstruction performance of the constructed sensing matrices with different sparsity.In each test,reconstruction frequencies are computed by 1000-times statistical experiments.

Fig.2.An example of sparse signal with N=200 and k=10.

Firstly,the signals with different length and identical sparsity are randomly generated.We uniformly chooseNfrom 200 to 1000 with an interval of 200.Set the sparsity level of the signalβ=0.1,thenk=βN.Suppose the sparsity level of the constructed sensing matrices bed=0.25.For each sparse signal,the Bernoulli,Gaussian,CS-LDPC and the constructed matrices are respectively used as the sensing matrices.For each type of the sensing matrix,we respectively use the measurement numbersMto be 2.5k,3k,4k,5kand the corresponding reconstruction frequencies are shown in Table I.

TABLE I RECONSTRUCTION FREQUENCIES FOR RANDOM SIGNALS WITH DIFFERENT LENGTHS(β=0.1,d=0.25)

In Table I,the first column represents the type of the sensing matrix.The second columnMrepresents measurement numbers.Those data from the third column to the seventh column respectively show the reconstruction frequencies for the sparse signals with different lengths.According to this table,the reconstruction frequencies of the constructed sensing matrices are higher than those of Bernoulli,Gaussian and CSLDPC matrices for differentMandN.For example,whenM=3kandN=600,the reconstruction frequencies are respectively 0.214,0.188,0.109 and 0.999,shown in the bold font,for four types matrices.It is obvious that the constructed sensing matrices have better reconstruction performance than the other three sensing matrices.

To intuitively illustrate the reconstruction performance of four types of sensing matrices,Fig.3 shows the change of the reconstruction frequencies with the parameterM/kforN=400.From Fig.3,to arrive at high reconstruction frequency,the constructed sensing matrices need fewer measurements than those of Bernoulli,Gaussian and CS-LDPC matrices.

When the measurements are corrupted by the Gaussian noise with mean value 0 and variance 0.01,Fig.4 shows the change of reconstruction frequencies of four types of sensing matrices.In the experiment,N=400,β=0.1 andd=0.2.From Fig.4,we can find that the constructed sensing matrices need fewer measurements than those of Bernoulli,Gaussian and CS-LDPC matrices to arrive at high reconstruction frequency for the noisy measurements.

In addition,experimental results for the signals with different sparsity levels illustrate that the constructed sensing matrices have better reconstruction performance,see Table II.

B.The Reconstructions for the Constructed Sensing Matrices With Different Sparsity

Fig.3.Reconstruction frequencies for the measurements without noise(N=400).

Fig.4.Reconstruction frequencies for noisy measurements(N=400).

The above experimental results suggest that the constructed sensing matrices have better reconstruction performance.The reasons are analyzed as follows.1)Comparisons with dense Gaussian and Bernoulli sensing matrices:When the constructed sparse sensing matrices can extract the sketch of the underlying signal,dense sensing matrices with the same dimensions can also extract its sketch.However,dense sensing matrices have some superfluous extractions of signal components,which will resist signal reconstruction.2)Comparisons with CS-LDPC sensing matrices:According to our constructions,the constructed sensing matrices reduce the mutual coherence and further satisfy StRIP property under certain condition,which will lead to the better reconstruction performance.

TABLE II RECONSTRUCTION FREQUENCIES FOR RANDOM SIGNALS WITH DIFFERENT SPARSITY LEVELS(N=400,d=0.2)

TABLE III RECONSTRUCTION FREQUENCIES FOR SPARSE SENSING MATRICES WITH DIFFERENT SPARSITY d(N=400,k=40,M=120)

C.Energy Consumption of Data Gathering Methods Based on Four Sensing Matrices

In data gathering of WSNs,energy consumption of the sensor nodes includes two aspects,acquiring the measurements and transmitting the measurements to the sink node.Assume thatE1denotes the energy consumed by the sensor nodes to acquire the measurements,E2represents the energy consumption of transmitting the measurements to the sink node,andEillustrates the total energy consumption,and then the following equation can be concluded.

SinceE2is the same for the data gathering methods based on four sensing matrices when the measurement numbers are the same,the total energy consumptionEis determined byE1.Assume that the energy consumption of each communication is denoted byEe,then the reconstruction frequencies and energy consumptionsE1for four data gathering methods(N=200,k=20,d=0.2)are listed in Table IV.

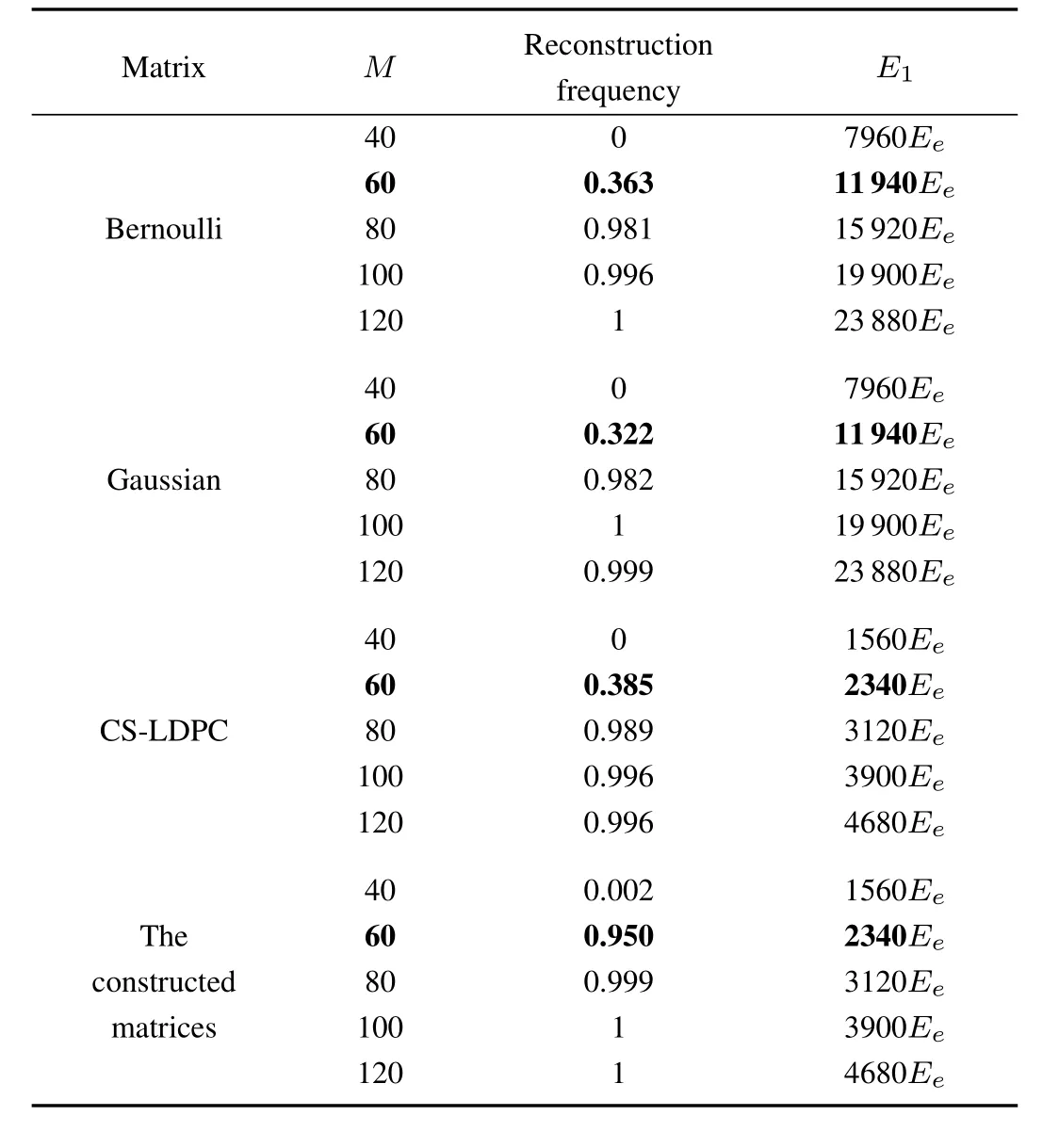
TABLE IV COMPARISONS WITH FOUR SENSING MATRICES(N=200,k=20,d=0.2)

In Table IV,the first column gives the type of the measurement matrices used in data gathering.The second columnMrepresents the rounds of data gathering.The third column lists the reconstruction frequency among 1000-times statistical experiments for each type of measurement matrix and differentM.The fourth column illustrates the corresponding energy consumptions.We takeM=60 marked in bold font as an example to illustrate from two aspects.1)Reconstruction frequencies:The Bernoulli,Gaussian,CS-LDPC and the constructed measurements are respectively 0.363,0.322,0.385 and 0.950.2)Energy consumption:Energy consumption of the Bernoulli and Gaussian measurements is 11940Ee,and that of the CS-LDPC and the constructed measurements is 2340Ee.For data gathering methods based on the Gaussian and Bernoulli sensing,the sensor node needsN−1 communications with other nodes for obtaining a measurement,and the sink node can receiveMmeasurements,then we can concludeE1=M(N−1)Ee.ForM=60,E1=60(200−1)Ee=11940Ee.While the sparsity level of CS-LDPC and the constructed matrix is0.2,these two data gathering methods only need the energy consumptionE1=M(0.2N−1)Ee.ForM=60,E1=60(0.2×200−1)Ee=2340Ee,while reconstruction frequencies are 0.385,0.950 for CS-LDPC and the constructed RLDPC matrix.Therefore,when almost the same reconstruction quality is achieved,the proposed method can reduce energy consumption than the other three methods.

To illustrate the change of energy consumption withd,Fig.5 shows the energy consumption whendis 0.1,0.15,0.2 and 0.25,respectively(Ee=1).From this figure,we can find that the energy consumption will increase with the increasing ofd.

Fig.5.The change in energy consumption with d.

V I.CONCLUSION

In WSNs community,it is a great challenge to balance energy consumption of sensor nodes whose imbalance may shorten the lifetime of the network inevitably.The data gathering methods based on uniform random sensing can reduce energy consumption of sensor nodes.However,the randomness and density of classical random matrices will lead to difficult implementations,high computation complexity,and large storage spaces.In view of this,some deterministic sparse sensing matrices are constructed.However,it is difficult to guarantee the performance of sensing matrix by the acknowledged metrics.In this paper,we construct a class of deterministic sparse sensing matrices having small mutual coherence and satisfying StRIP via RLDPC matrix,and propose a data gathering method based on RLDPC matrix.We deduce the condition that RLDPC matrix satisfies StRIP with high probability and the lower bound of the sparsity of sensing matrix.And we also prove that the constructed sensing matrix has the same scale of measurement numbers as the dense measurement ensembles.Experimental results verify that the constructed sensing matrices have better reconstruction performance,compared to the Gaussian,Bernoulli,and CSLDPC matrices.And they also show that the data gathering based on RLDPC matrix can reduce energy consumption of sensor nodes compared with those via other sensing matrices on the premise of the same reconstruction performance.We believe that the constructed sensing matrices and the proposed data gathering method are attractive due to their good reconstruction performance and energy consumption.

[1]R.S.Dilmaghani,H.Bobarshad,M.Ghavami,S.Choobkar,and C.Wolfe,“Wireless sensor networks for monitoring physiological signals of multiple patients,”IEEE Trans.Biomed.Circ.Syst.,vol.5,no.4,pp.347−356,Aug.2011.

[2]C.Perera,A.Zaslavsky,P.Christen,and D.Georgakopoulos,“Context aware computing for the internet of things:A survey,”IEEE Commun.Surv.Tutor.,vol.16,no.1,pp.414−454,Jan.−Mar.2014.

[3]X.J.Ding,Y.Tian,and Y.Yu,“A real-time big data gathering algorithm based on indoor wireless sensor networks for risk analysis of industrial operations,”IEEE Trans.Ind.Inf.,vol.12,no.3,pp.1232−1242,Jun.2016.

[4]D.Takaishi,H.Nishiyama,N.Kato,and R.M iura,“Toward energy gathering in densely distributed sensor networks,”IEEE Trans.Emerg.Top.Comp.,vol.2,no.3,pp.388−397,Sep.2014.

[5]C.Luo,F.Wu,J.Sun,and C.W.Chen,“Efficient measurement generation and pervasive sparsity for compressive data gathering,”IEEE Trans.Wirel.Commun.,vol.9,no.12,pp.3728−3738,Dec.2010.

[6]A.F.Liu,L.X.Cai,T.H.Luan,and A.Ranabahu,“QoS-aware data collection in wireless sensor networks,”Int.J.Distrib.Sensor Netw.,vol.2015,pp.Article ID 769083,2015.

[7]S.Lindsey,C.Raghavendra,and K.M.Sivalingam,“Data gathering algorithms in sensor networks using energy metrics,”IEEE Trans.Parall.Distrib.Syst.,vol.13,no.9,pp.924−935,Sep.2002.

[8]M.Khan,G.Pandurangan,and V.S.A.Kumar,“Distributed algorithms for constructing approximate minimum spanning trees in wireless sensor networks,”IEEE Trans.Parall.Distrib.Syst.,vol.20,no.1,pp.124−139,Jan.2009.

[9]Y.S.Liu and Z.Wang,“A prediction-based data collection method in wireless sensor network using Kalman filter,”ICIC Express Lett.,vol.2.no.6,pp.1439−1446,Dec.2011.

[10]O.Younisand S.Fahmy,“HEED:A hybrid,energy-efficient,distributed clustering approach for ad hoc sensor networks,”IEEE Trans.Mob.Comp.,vol.3,no.4,pp.366−379,Oct.−Dec.2004.

[11]H.Lin and H.Uster,“Exact and heuristic algorithms for data-gathering cluster-based wireless sensor network design problem,”IEEE/ACM Trans.Netw.,vol.22,no.3,pp.903−916,Jun.2014.

[12]X.X.Song and G.M.Shi,“Data gathering of WSNs based on sequential compressed sensing and sparse sensing,”Int.Rev.Comp.Softw.,vol.7,no.1,pp.397−402,Jan.2012.

[13]D.L.Donoho,“Compressed sensing,”IEEE Trans.Inf.Theory,vol.52,no.4,pp.1289−1306,Apr.2006.

[14]E.J.Candes and M.B.Wakin,“An introduction to compressive sampling,”IEEE Signal Process.Mag.,vol.25,no.2,pp.21−30,Mar.2008.

[15]A.Aminiand F.Marvasti,“Deterministic construction of binary,bipolar,and ternary compressed sensing matrices,”IEEE Trans.Inf.Theory,vol.57,no.4,pp.2360−2370,Apr.2011.

[16]S.Jafarpour,W.Y.Xu,B.Hassibi,and R.Calderbank,“Efficient and robust compressed sensing using optimized expander graphs,”IEEE Trans.Inf.Theory,vol.55,no.9,pp.4299−4308,Sep.2009.

[17]H.F.Zheng,F.Yang,X.H.Tian,X.Y.Gan,X.B.Wang,and S.L.Xiao,“Data gathering with compressive sensing in wireless sensor networks:a random walk based approach,”IEEE Trans.Parall.Distrib.Syst.,vol.26,no.1,pp.35−44,Jan.2015.

[18]L.Applebaum,S.D.Howard,S.Searle,and R.Calderbank,“Chirp sensing codes:deterministic compressed sensing measurements for fast recovery,”Appl.Comput.Harm.Anal.,vol.26,no.2,pp.283−290,Mar.2009.

[19]N.Ailon and E.Liberty,“Fast dimension reduction using Rademacher series on dual BCH codes,”inProc.19th Annu.ACM-SIAM Symp.Discrete Algorithms(SODA),San Francisco,California,USA,2008,pp.1−9.

[20]J.Haupt,W.U.Bajwa,G.Raz,and R.Nowak,“Toeplitz compressed sensing matrices with applications to sparse channel estimation,”IEEE Trans.Inf.Theory,vol.56,no.11,pp.5862−5875,Nov.2010.

[21]R.Calderbank,S.Howard,and S.Jafarpour,“Construction of a large class of deterministic sensing matrices that satisfy a statistical isometry property,”IEEE J.Sel.Top.Signal Process.,vol.4,no.2,pp.358−374,Apr.2010.

[22]S.Hong,H.Park,B.Shin,J.S.No,and H.Chung,“A new performance measure usingk-set correlation for compressed sensing matrices,”IEEE Signal Process.Lett.,vol.19,no.3,pp.143−146,Mar.2012.

[23]R.Berinde,A.C.Gilbert,P.Indyk,H.Karloff,and M.J.Strauss,“Combining geometry and combinatorics:A unified approach to sparse signal recovery,”inProc.46th Annu.Allerton Conf.Communication,Control,and Computing,Urbana-Champaign,IL,USA,2008,pp.798−805.

[24]D.Baron,S.Sarvotham,and R.G.Baraniuk,“Bayesian compressive sensing via belief propagation,”IEEE Trans.Signal Process.,vol.58,no.1,pp.269−280,Jan.2010.

[25]W.Wang,M.J.Wainwright,and K.Ramchandran,“Information theoretic limits on sparse signal recovery:dense versus sparse measurement matrices,”IEEE Trans.Inf.Theory,vol.56,no.6,pp.2967−2979,Jun.2010.

[26]E.J.Candes and T.Tao,“Near-optimal signal recovery from random projections:Universal encoding strategies?,”IEEE Trans.Inf.Theory,vol.52,no.12,pp.5406−5425,Dec.2006.

[27]R.Gallager,“Low-density parity-check codes,”IEEE Trans.Inf.Theory,vol.8,no.1,pp.21−28,Jan.1962.

[28]S.Lin and D.J.Costello Jr,Error Control Coding.2nd ed.New York,USA:Prentice Hall,2004.

[29]M.J.Wainwright,E.Maneva,and E.Martinian,“Lossy source compression using low-density generator matrix codes:Analysis and algorithms,”IEEE Trans.Inf.Theory,vol.56,no.3,pp.1351−1368,Mar.2010.

[30]L.Gan,C.Ling,T.T.Do,and T.D.Tran,“Analysis of the statistical restricted isometry property for deterministic sensing matrices using Stein’s method,”[Online].Available:http://dsp.rice.edu/sites/dsp.rice.edu/files/cs/Gan StatRIP.pdf,September 22,2017.

[31]D.L.Donoho and Y.Tsaig, “Fast solution ofℓ1-norm minimization problems when the solution may be sparse,”IEEE Trans.Inf.Theory,vol.54,no.11,pp.4789−4812,Nov.2008.

[32]M.S.Asif and J.Romberg, “Dynamic updating forℓ1minimization,”IEEE J.Sel.Top.Signal Process.,vol.4,no.2,pp.421−434,Apr.2010.