基于GPD模型的粮食作物巨灾的定量界定——以我国稻谷巨灾界定为例*

梁来存，皮友静

(1.广西财经学院 信息与统计学院，广西 南宁 530003；2. 广西财经学院 图书馆，广西 南宁 530003)

一、引言与文献综述

十八届三中全会通过的《中共中央关于全面深化改革若干重大问题的决定》提出了“完善保险补偿机制，建立巨灾保险制度”。2016年“中央一号文件”要求“进一步完善农业保险大灾风险分散机制”。2017年1月10日，中共中央、国务院发布《关于推进防灾减灾救灾体制机制改革的意见》，明确提出要加快巨灾保险制度建设，积极推进农业保险和农村住房保险等工作。粮食作物是农作物中的主导作物，在我国农业中处于不可动摇的基础地位。为了积极开展粮食作物的巨灾保险业务，首先需要对粮食作物的巨灾进行明确界定，这是合理确定“触发条件”、开发巨灾保险产品、进行巨灾风险管理等方面的现实需要，具有重要的意义。

巨灾没有严格统一的定义，并且一直随着社会的发展而变更(王和，2005[1]50-52)。巨灾的界定，可以分为两类：一类是定性的界定。这在国内外较为统一。一般根据其特点定义为：巨灾是指低概率、严重的、剧烈的极端因素造成人、财、物巨大损失的事件(OECD，2004[2]86-95；Erik Banks，2005[3]110-115； “地方政府应对重大自然灾害对策研究”课题组,2010[4]74-82;许飞琼，2012[5]82-88; 何振,2012[6]22-26)。更多地，是就巨灾进行定量的刻画。巨灾的定量界定，主要是从四个角度来界定：一是从一个国家或地区的角度，指死亡人数、经济损失达到一定程度的事件。Gad-el-Hak(2008)[7]1-4将灾害分为五级，其中死亡人数超过1 000人或受灾面积超过100km2的属于巨灾。汤爱平等(1999)[8]61-65从灾害损失占国内生产总值的比重、重伤和死亡人数的百分比按国家、省(市)和县(市)三级进行了界定。史培军等(2009)[9]428-435则提出死亡10 000人以上、直接经济损失1 000亿元人民币以上、成灾面积10万km2以上三条标准，认为只要符合其中两条即可划定为巨灾。二是从保险业的角度，给保险业的损失达到一定程度的事件。J.David Cummins, Neil Doherty 和 Anita Lo(2002)[10]557-583等认为巨灾是每次给保险业带来超过 100 亿美元损失的事件。美国保险服务局(ISO)的财产理赔服务部按照1998年价格将巨灾风险定义为“导致财产直接保险损失超过2 500万美元并影响到大范围保险人和被保险人的事件”。标准普尔(1999)把巨灾定义为导致保险损失超过 500万美元的一个或一系列相关风险事件。瑞士再保险的sigma杂志将巨灾风险界定为由自然力量引起的，造成至少3 870万美元(2005年的标准)的保险损失，且涉及大量保单和众多保险人的事件。三是从保险公司的角度，相对于保险公司的偿付能力而言的，即当保险赔款过多导致超过保险公司一般偿付能力的风险称为巨灾风险。四是从工作需要的角度。我国民政系统规定：作物收成因灾减产较少为受灾；因灾减产幅度在30%以上为成灾，其中，减产50%以上为重灾。

在巨灾界定方法方面，有的以对数正态分布拟合巨灾损失的分布(田玲，2016[11]141-150)，但更多的是极值理论GPD来有效拟合巨灾风险尾部损失，应用于地震(卓志，2013[12]13-19；朱钰，2016)、洪水(肖海清、孟生旺，2013[13]240-246；邹辉文，2017)、台风(周延、屠海平，2017[14]69-80)等巨灾风险研究。

我国农业保险由保险公司承保，所以，只有从保险公司角度的定量界定才适合粮食作物巨灾保险的需要。考虑到无论何种自然灾害，或者其致灾方式如何，它对粮食作物的影响程度最终都会反映在单产的变化幅度上。因此，应当从单产的视角来界定粮食作物巨灾。那么，如何从单产方面定量界定巨灾呢？这是研究巨灾保险必须首先解决的问题。由于粮食作物灾损数据的缺乏，本文以我国稻谷为例，在合理推算灾损数据的基础上，对灾损数据的分布形式进行诊断，据此选取GPD的分布形式；再对GPD的门限值进行初步估计，并建立GPD模型进行检验以最终确定门限值；最后再对确定的门限值从理论上、实践上进行了验证。

二、研究方法

(一)模型选择——GPD模型

极值理论为灾损数据中的极端值的数据处理提供了一种较好选择，它不研究数据序列的整体分布情况，只关心序列的尾部分布情况，也就是极端值分布。粮食作物巨灾事件是由极端气候引起的，属于极值事件，所以，可基于极值理论对粮食作物巨灾进行定量界定。

对于数据的尾部分布，极值理论利用广义极值分布(general extreme value distribution)或者广义帕累托分布(general pareto distribution)来描述。相应地，在极值分析中，前者称为GEV模型，后者称为GPD模型。GEV模型是首先将数据分为若干组，从各组中分别选取最大的一个数据，合并构成一个新的数据组，再对该新的数据组进行分析建模。而GPD模型则不同，它是首先设定一个门限值，把观测值中超过该门限值的数据集合成新的数据组，再基于该数据组建模。比较来看，GPD模型要求的原始数据可以少一些，它能够充分有效地利用有限的数据。粮食作物的灾损数据有限，因此，这里选择GPD模型来界定巨灾。

(二)粮食作物灾损数据的获取

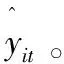
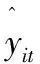
(1)

(三)灾损数据厚尾性的诊断

GPD具有厚尾分布的特征。对于粮食作物灾损数据，需要分析该组数据是否具有厚尾性的分布特征。诊断分布的厚尾性可以采用如下的方法。

1．样本经验平均超出函数图(EMEF图)

样本经验超出函数为：

(2)

2．指数QQ图

指数QQ图给出序列分位数分布相对于指数分布的异同。如果QQ图上凸，表明相对于理论分位数，经验分位数增长快，该分布是厚尾的；如果QQ图下凸，该分布就是薄尾的；如果QQ图大致形成一条直线，则该分布近似服从指数分布。

如果上述诊断结果认定灾损数据具有厚尾性，那么，有理由选择GPD作为该灾损数据的尾部的分布形式。

(四)巨灾界定值的初步估计

1.巨灾界定的理论依据

Balkema & Dehann(1974),Pickands(1975)证明了超额灾损数据zi(=xi-μ)的分布函数在MDA条件下收敛于GPD。即当μ→x0时，sup{Fμ(z)-Gξ,β(μ)(z)|:0zx0-μ}→0。这就是PBDH定理。该定理的统计意义在于，可以用GPD来拟合高出门限值的那一部分数据。

可见，只有估计了门限值μ，才能依据前述的灾损数据和门限值μ，确定巨灾年份，并得到超额灾损数据z。依据PBDH定理，超额灾损数据z趋于GPD，据此计算z的期望值E(z)，则E(z)+μ为巨灾数据的期望值。所以，要计算巨灾年份巨灾数据的期望值，厘定巨灾保险的费率，估计门限值μ是必要的。

2.巨灾界定值的初步估计法

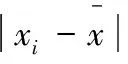
(五)巨灾界定值的检验和确定

根据GPD模型，对于超额灾损数据z=)z1,z2,…,zNμ}(z=x-μ)，采用极大似然估计法，其对数似然函数为：

建立的GPD模型还需要进行检验。根据V. Choulakian和M.S.Stephens(2001)[15]478-484的研究，检验GPD模型可使用假设检验法。原假设H0：样本来自于GPD，并计算统计量：

(3)

(4)

这里，Fi=F(zNμ.i)，zNμ.1,zNμ.2,…,zNμ.i,…,zNμ.Nμ为z1,z2,…，zNμ的递增顺序统计量。查阅GPD检验值表，根据W2、A2的值以决定是否接受原假设H0。

在第(四)步中，已经得到了巨灾界定值的初步估计值。对该值及其附近可能的门限值，逐一进行上述检验，直到检验通过为止，这时的巨灾界定估计值即为最终确定的巨灾界定值。

三、实证研究

假定农民以单产投保，在国家投入和技术创新变化趋势等稳定的前提下，单产的变化幅度反映了所有自然风险对稻谷作物的影响程度。这里以我国稻谷为例，从单产视角研究我国稻谷作物的巨灾界定值。

(一)数据搜集与灾损数据推算

1．数据搜集

根据相关年份的《中国农村统计年鉴》，可以搜集到如表1所示的我国30个省(市、区)稻谷作物1979—2015年分省、分年的实际单产数据yit(公斤/公顷)。

以省(市、区)为单位，为了得到各省(市、区)各年的单产趋势值，采用趋势方程拟合法。取1979—2015年各年的t为1～37(其中，广东、海南只有1988—2015年的单产数据，故t取1～28；四川、重庆只有1997—2015年的单产数据，故t取1～19)，根据各省(市、区)的实际单产数据，将各省(市、区)所拟合的单产趋势方程列于表1中。

从表1来看，拟合精度指标MAPE值都小于10，符合精度要求，可以接受上述所建立的趋势方程。

3．灾损数据的推算

将各年的对应t值代入表1的趋势方程中，即可得到各省(市、区)各年的趋势单产值。把各省(市、区)每年的实际单产与相应的趋势单产代入式(1)，便得到灾损数据。对于这些灾损数据，如果分省份分析，样本容量为37，广东、海南的样本容量只有28，四川、重庆只有19，样本太小，无法对灾损数据的分布形式进行较准确的判断。

假定农民以单产投保，在巨灾的影响下，单产的变化在各省(市、区)之间仍然具有可比性。以高单产地区为例，与低单产地区相比，一方面，由于单产相对较高，在同样灾害的影响下，单产的下降幅度会比较大；但另一方面，高单产地区的基础设施往往相对完善，抵御自然灾害的能力相对较强，单产的下降幅度会比较小。综合这两个方面，可以认为各地区间的单产变化具有可比性。因此，把各省(市、区)的灾损数据作为一个整体进行分析，这是合理的。

将得到的灾损数据按组距5%进行等距分组，将灾损数据进行整理，得到如图1所示的灾损数据次数分布直方图：

表1 各省(市、区)的单产趋势方程表

省(市、区)拟合的趋势方程拟合优度R2MAPE北京天津河北山西内蒙古辽宁吉林黑龙江上海江苏浙江安徽福建江西山东河南湖北湖南广东广西海南重庆四川贵州云南西藏陕西甘肃宁夏新疆y＾1t=4579．9t0．1147y＾2t=-4．4273t2+255．68t+3764．5y＾3t=246．55lnt+5430．1y＾4t=1．7653t2-99．468t+6573．8y＾5t=-1．5805t2+228．84t+1631．5y＾6t=0．2069t2+45．194t+6020．6y＾7t=3798．6t0．2029y＾8t=-1．8625t2+188．41t+2687．4y＾9t=-3．4187t2+235．55t+4318．8y＾10t=1165．7lnt+4246．6y＾11t=0．814t2+31．853t+5083．6y＾12t=706．39lnt+3690．4y＾13t=0．1886t2+52．525t+4058．6y＾14t=-0．2264t2+72．272t+3678y＾15t=-1．9714t2+193．29t+3983．7y＾16t=97．951t+4267．4y＾17t=-2．6495t2+194．59t+4369．9y＾18t=603．88lnt+4169．9y＾19t=297．49lnt+4695．1y＾20t=-1．0541t2+94．8t+3484．2y＾21t=636．66lnt+2541．6y＾22t=-2．2672t2+102．19t+6318y＾23t=6．7046t2-119．23t+7774．6y＾24t=-3．094t2+176．9t+3597．4y＾25t=-2．0375t2+145．1t+3437．1y＾26t=66．691t+3263．7y＾27t=0．6985t2+34．947t+4956．6y＾28t=-6．9031t2+370．99t+2584．2y＾29t=6669．2t0．0679y＾30t=1921t0．41490．45720．59570．08480．10020．90610．38020．61780．86620．85360．76200．72880．66370．83330．78110．67310．68910．85450．68740．26510．74870．69510．55140．52770．57000．82450．51820．51980．70310．26990．87168．01129．84019．34838．82339．24297．99369．44668．97135．52535．67584．94815．85813．64605．65408．18039．28924．92313．49705．50835．67997．17903．32481．90339．52324．79688．77549．43139．32027．32149．3401

(二)灾损数据的分布特征：厚尾性

对于灾损数据，是否存在巨灾的界定值，还需要进行诊断，也就是厚尾性诊断。现对上述灾损数据进行初步分析，分析结果列于表2中：

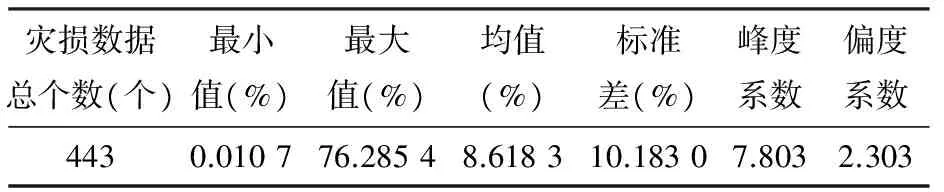
表2 我国稻谷灾损数据的统计分析指标

表2表明，灾损数据总共有443个，最小值为0.010 7%，即相对于正常单产，平均单产减少了0.010 7%，显然这不是巨灾。最大值为76.285 4%，即相对正常单产平均单产减少了76.285 4%，无疑这属于遭受巨灾导致的减产。

峰度系数为7.803，远远大于正态分布的峰度系数3，不能用常用的正态分布作为灾损数据的分布形式。偏度系数为2.303>0，呈右偏分布。这就是说，我国稻谷的灾损数据序列有极端值存在，即序列存在巨灾数据。

利用式(2)，计算与每一个可能门限值μ相对应的样本经验超出函数值en(μ)，据此做出灾损数据的样本经验平均超出函数图(即EMEF图)，如图2所示：

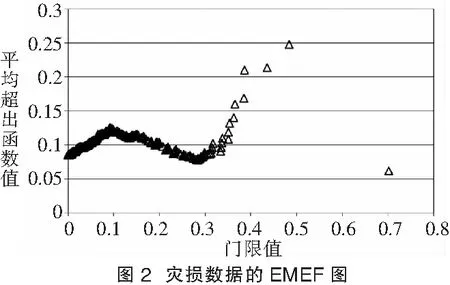
从图2的样本经验平均超出函数图来看，图形呈明显的向上趋势，说明分布是厚尾的。

再利用SPSS作指数QQ图，如图3所示：

图3的指数QQ图表明，图形呈上凸状，据此判断该分布为厚尾分布。

三种方法都得出了一致的结论：该灾损数据呈厚尾分布，存在巨灾数据。那么，巨灾数据的界定值，即门限值取多大呢？

(三)门限值的估计与确定

对于上述的灾损数据，样本平均超出函数法很难精确估计门限值。根据图2可以粗略地估计门限值应当在0.08～0.26之间，因为这个区间内的数值，都能保证其后数据呈一正斜率的线性趋势。

采用正态近似法估计时，参照样本平均超出函数法的估计结果，门限值只取从0.08～0.26之间，且每隔0.015估计一次。在计算Φ(x)时，均值与标准差都根据全体灾损数据计算得到。现将计算结果列于表3中。

从表3分析可知，门限值取0.125及其以下值时，Φ(x)<1-Nμ/n；门限值取0.140及其以上值时，Φ(x)>1-Nμ/n。我们取满足Φ(x)<1-Nμ/n的最大的x作为门限值，门限值应当在0.125～0.140之间。

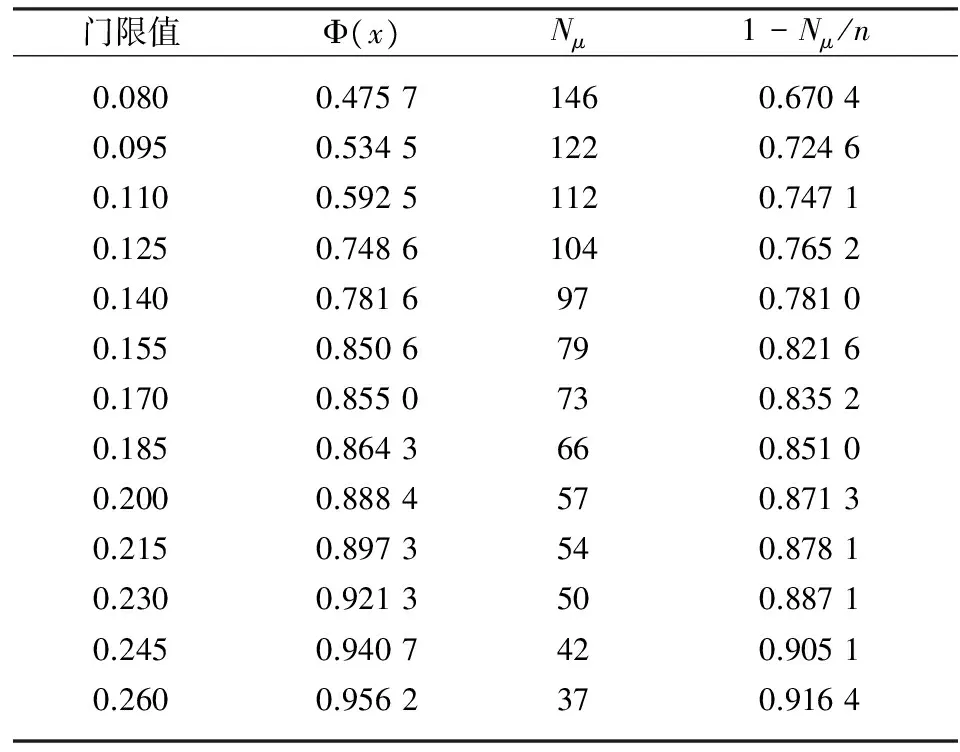
表3 正态近似法估计门限值

再采用峰度法，利用MATLAB R2017a软件，可以得到门限值为0.133 7，大于该门限值的灾损数据有98个。除去这98个巨灾数据，余留下来的灾损数据的峰度系数为2.977 1，相当于正态分布的峰度系数3。据此可以估计，我国稻谷巨灾的界定值即门限值在0.133 7附近，巨灾数据有98个左右。

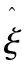
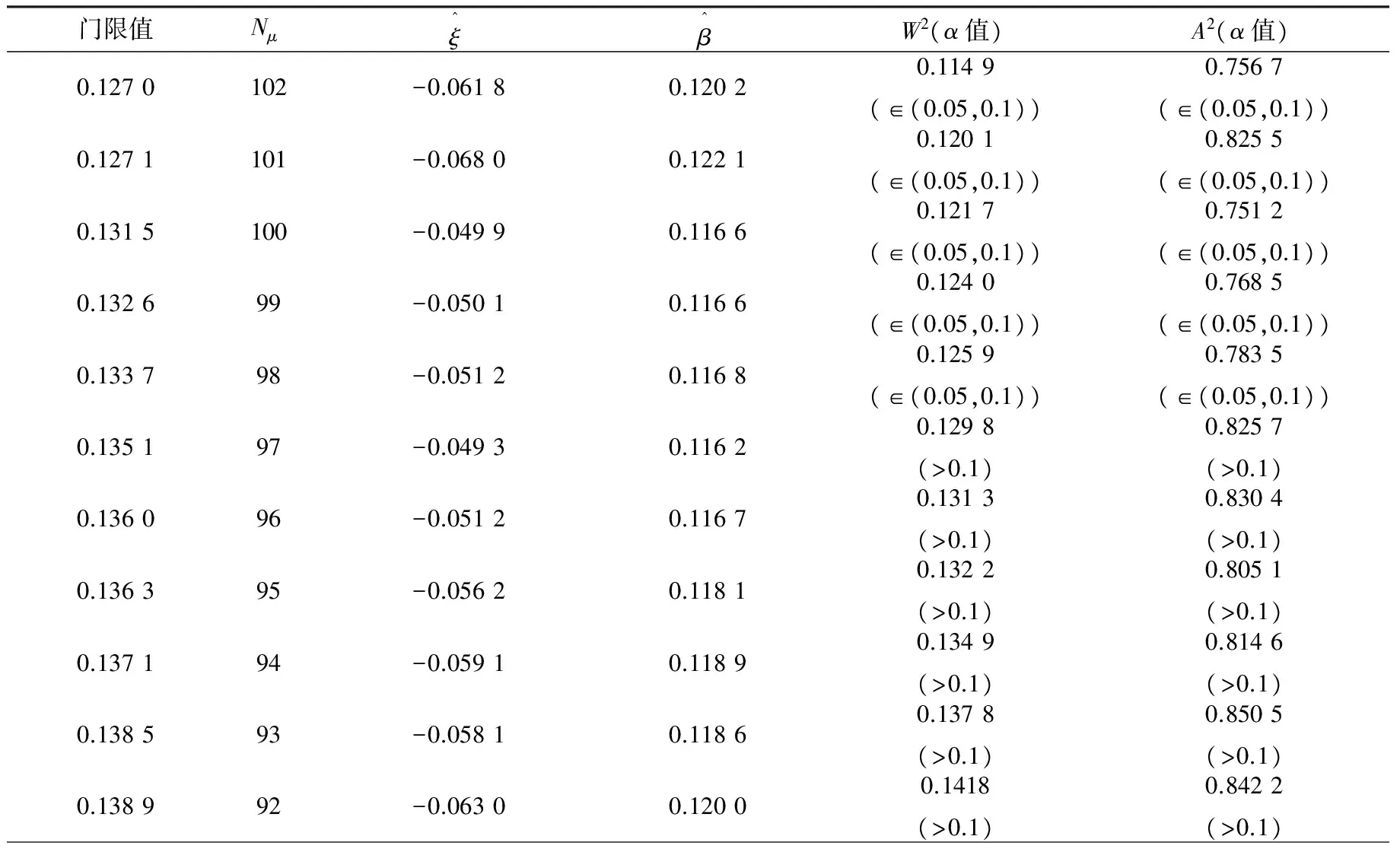
表4 门限值及其参数估计与检验表

注：对应于ξ、α的W2、A2临界值来源于V. Choulakian & M. A. Stephens(2001)模拟得到的临界值表。当ξ取其他值时，临界值通过线性插值法求出。

在表4中，α值就是假设检验中的P值，当α值很小时，就有理由拒绝原假设H0。当门限值μ≤0.133 7时，在10%的显著性水平上拒绝原假设H0，即相应的超额灾损数据不服从GPD。当μ≥0.135 1时，在10%的显著性水平上接受原假设H0，即相应的超额灾损数据服从GPD。为了尽可能扩大服从GPD的样本的容量，确定门限值μ=0.135 1，这就是稻谷单产巨灾的界定值。超过该单产巨灾界定值的灾损数据，均为巨灾数据。

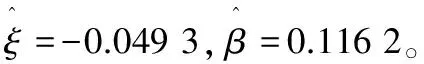
(四)实证结论的检验

上述实证已经得出结论：我国稻谷单产巨灾的界定值为0.135 1。也就是说，相对于正常单产(即趋势单产)，当实际单产下降幅度达到13.51%及其以上时，即认定巨灾发生。那么，这一界定结论是否正确合理呢？

1.理论上，PBDH定理得到了验证

仍以X表示灾损数据，当μ=0.135 1时，对超额灾损数据X-μ的分布形式进行分析。

可供选择的分布形式很多，常用的有正态分布、指数分布、逻辑分布、均匀分布、伽玛分布、GPD等。检验统计量能对模型的分布函数和经验分布函数之间的接近程度进行度量。这里采用三个检验统计量，即Cramer-von Mises (W2)统计量，Watson (U2)统计量和Anderson-Darling (A2)统计量分别进行检验，将分布的三个检验统计量的检验结果一并列于表5中。

表5 X-μ超额灾损数据的最优分布检验

在表5中，第(1)、(4)、(7)列为各检验统计量的值，第(2)、(5)、(8)列为各检验统计量的调整值，第(3)、(6)、(9)列为根据各统计量就分布进行假设检验时的P值。选出X-μ的分布形式的依据主要是两个：比较不同分布下的检验统计量的值，以及假设检验对应的P值。对于同一检验统计量，得出的最优分布列于最后一行的检验结论中。

检验结论表明，三个检验统计量得出了一致的结论，即X-μ的最优分布为GPD。这一结论与PBDH定理相一致，这也反映了μ=0.135 1是正确的。

2.实践上，实证结论与巨灾定义相吻合

上述的实证研究选取了1979—2015年间我国30个省(市、区)37年的数据。其中，广东、海南只有1988—2015年28年的数据，四川、重庆只有1997—2015年19年的数据。这样，样本容量为1 056。根据上述实证研究的结果，当巨灾界定值，即门限值为μ=0.135 1时，巨灾数据共有97个。97∶1056≈1∶11，这就是说，如果将μ=0.135 1定义为巨灾界定值，这样的巨灾大致每十一年发生一次。“十年一遇”，这与巨灾是低概率事件的定性定义是相吻合的。

四、结论

粮食作物巨灾事件属于极值事件，应当基于极值理论界定巨灾。上述研究表明，无论是从理论上还是从实践上来分析，该界定方法确定的巨灾界定值都能经得起检验。巨灾界定值的确定，确保了超额灾损数据的GPD分布形式，从而达到了从保险公司视角定量界定巨灾的目的。它为保险公司确定粮食作物巨灾保险的“触发条件”、费率厘定、产品及衍生产品的研发以及巨灾管理等方面提供了依据。所以，基于极值理论研究粮食作物的巨灾界定是科学合理的。

基于极值理论界定巨灾的方法是：依据趋势模型法可以得到粮食作物的趋势单产，推算出灾损数据；在对灾损数据进行厚尾性诊断的基础上，利用样本平均超出函数法、正态近似方法、峰度法对灾损数据的门限值进行初步估计；对于门限值的各个初估值，利用极大似然法、概率加权矩方法或EMP方法估计GPD模型，并对模型进行假设检验；GPD模型检验通过的相应门限值为最终确定的门限值，即为粮食作物巨灾的定量界定值。

粮食作物巨灾的界定值，既可以将全国粮食作物作为研究对象，得出全国粮食作物巨灾的界定值，也可以省(市、区)为单位，得出相应省(市、区)粮食作物的巨灾界定值，还可以县、乡为单位，测算相应的巨灾界定值。

[1]王和. 对建立我国巨灾保险制度的思考[J]. 中国金融，2005(7).

[2]OECD. Large-scale disaster：Lessons learned[M]. Paris：OECD Publishing,2004.

[3]Erik Banks. Catastrophic risk: Analysis and management[M]. New Jersey:John Wiley & Sons, Ltd，2005.

[4]“地方政府应对重大自然灾害对策研究”课题组.湖南地方政府应对重大自然灾害对策调研及其思考[J].湘潭大学学报(哲学社会科学版),2010(4).

[5]许飞琼.巨灾、巨灾保险与中国模式[J].统计研究，2012(6).

[6]何振,唐湘林,张卓.地方政府应对重大自然灾害的行政问责探究[J].湘潭大学学报(哲学社会科学版),2012(2).

[7]Mohamed Gad-el-Hak. Large-scale disasters:prediction， control， and mitigation[M].New York:Cambridge University Press,2008.

[8]汤爱平，谢礼立，陶夏新,等. 自然灾害的概念、等级[J].自然灾害学报，1999(3).

[9]史培军，李宁，叶谦,等. 全球环境变化与综合灾害风险防范研究[J].地球科学进展，2009(4).

[10]J David Cummins，Neil Doherty，Anita Lo.Can Insurers Pay for the “Big One”? Measuring the Capacity of the Insurance Market to Respond to Catastrophic Losses[J].Journal of Banking and Finance，2002,26(3).

[11]田玲，吴亚玲，沈祥成.基于CVaR的地震巨灾保险基金规模测算[J].经济评论，2016(4).

[12]卓志.巨灾风险厚尾分布：POT模型及其应用[J].保险研究，2013(8).

[13]肖海清，孟生旺.极值理论及其在巨灾再保险定价中的应用[J].数理统计与管理,2013(2).

[14]周延，屠海平.跨区域型台风巨灾保险基金设计[J].中国软科学，2017(6).

[15]Choulakian V,Stephens M A.Goodness-of-fit tests for the generalized pareto distribution[J].Technometrics,2001,43(4).