数学模型在金融资产配置中的应用
2018-01-24边灵玥
边灵玥
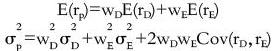
【摘要】本文首先介绍了资产配置的定义以及资产配置的必要性和重要性。其次讲解了资产配置自上而下的大致思路。接着定量地介绍了金融资产配置中三种不同的数学模型。最后反思现有模型的不足和未来模型的改进方向。
【关键词】资产配置 均值-方差模型 风险评价模型
【中图分类号】F8 【文献标识码】A 【文章编号】2095-3089(2018)48-0235-02
一、引言
资产配置是指资金在不同种类的金融资产之间进行分配的过程。资产配置的概念由来已久,名著《堂吉诃德》中的名句为大家所知晓——“不要把鸡蛋放在同一个篮子中”。投资者在被单一资产可观的收益率吸引时,却不能忽视投资单一资产承受的巨大风险。对于单一资产而言,收益和风险是相匹配的,并不存在高收益低风险的资产。因此如果投资者希望在不损失收益的情况下,降低资产风险,就需要进行分散投资,有效的进行资产配置——以合适的比例投资适当的资产组合。如此我们可以改善风险-收益比率,达到我们稳健投资的目的。
对于个人而言,进行合理的资产配置可以在保证可观的资产收益率的同时保证资产风险的可控。假设市场投资主体为理性投资者,都追求利益最大化,而市场具有客观的评价机制,这使得整个社会的资金具有更好的流通性和充分的使用效率,而最终达到资源优化配置的效果。
二、金融资产的配置思路
资产配置是自上而下的一个投资过程,大致思路如下:首先由投资者的风险偏好来决定以适当的比例将资金分配于资产配置风险资产和无风险资产之间,这里涉及到风险厌恶系数和无差异曲线的概念。无差异性表现在“曲线”上的每一点,即不同的资产配置组合对于投资者来说都是“无差异”的,即曲线上每个投资组合的收益和风险相匹配的效用值是相同的。我们可以由投资者的风险厌恶系数来计算出投资组合中投资风险资产的合适比例。
其次在风险类资产中的小类进行选择即确定投资组合的备选投资池应该如何进行选择资产种类。这里介绍一种通过选择逆周期性的投资标的而最大程度规避经济周期波动带来的不利风险的投资思路——“美林时钟”。该理论具体将经济划分为四个周期并对应于相应的逆周期投资标的,依次是:经济复苏期对应小盘股、房地产和新兴市场股票;经济过热期对应于大宗商品、发达市场股票、通胀保护债券;经济停滞期对应于大盘蓝筹股、短期国库券、成长型股票以及经济衰退期对应于中长期国债、公司债和價值型股票。而各类风险资产内部的相对比例则是由风险资产的证券特征来决定的,包括其期望收益率、方差、协方差等。在确定好投资的风险资产种类后,具体相对比例的计算将在第三部分详细说明。
最后是各小类风险资产内部中的证券选择,在实际操作中则会涉及到具体个股、具体债券等的证券选择。而具体的选择方法则根据投资者不同而不同。譬如在个股的选择上,投资者比较普遍的使用行业研究的方法:将个股按行业分类,研究同一行业的上中下游行业;研究该行业的市场格局、龙头企业等;最后研究行业中各家公司的财报、预期增长率等。
三、资产配置中的数学模型
在明确投资的风险资产种类范围后,具体各类资产的大类相对比例可由不同的数学模型进行定量分析,得到明确的配置比例。
1.固定比例的资产配置组合
在资产配置初期,投资者大多以固定比例进行资产配置。在仅考虑股票和债券这两种投资标的时,最常用而经典的配置方式是60/40投资组合,即在投资组合中持有60%的股票和40%的债券。当持有更多种类的风险资产时,有投资者则对每类资产分配1/N的权重,其中N为整个投资组合的风险种类总数,即对所有风险资产均匀分配。同时也有投资者依据自己的投资理念,对多种类的风险资产进行较为固定的配比,但在不同种类资产之间有所侧重。譬如著名的耶鲁捐赠基金投资人——大卫·斯文森,他在20余年期间保持了年均净收益率16%左右的优秀业绩。根据耶鲁捐赠金公开的近几年年度报告来看,投资组合中的各类资产占比较为固定,其中主要包括美国股票、国外股票、固定收益、房地产、自然资源和现金等其他类资产。
2.马科维兹资产组合选择模型
以投资组合的期望收益为纵轴、波动率为横轴绘制出的函数图像即为此两种投资标的的投资可行集。特别需要指出的是两种标的资产的协方差(大于两种资产标的则为协方差矩阵)会决定不同的投资可行集。当协方差为负时,投资组合的方差则会降低。更特殊的当相关系数ρ=-1时即完全负相关时存在零方差组合即可以完全对冲风险,此时最大化了分散投资的好处。由于对于任意风险水平,我们只关注期望收益率最高的组合集,因此将最小方差边界上方的点构成的集合称为风险资产有效边界。我们通过以无风险收益率为截距向风险资产有效边界做切线,切点即为最优风险组合。此时我们得到的报酬/波动性比率最高的一条资产配置线。最后我们可以通过投资者的风险厌恶系数和无差异曲线在风险资产与无风险资产之间确定最优组合。
3.风险平价模型
风险平价模型是指由风险的角度出发,给予投资组合中各类资产不同的权重,而实现各类不同资产在投资组合中所贡献的加权风险“平价”,即基本相当。风险贡献可以理解为各类资产的损失贡献。风险平价模型配置的不是“资产”而是“风险”。在模型中将资产价格的波动率作为衡量资产风险的指标,当资产价格服从或近似服从正态分布时,模型有较好的表现;相反当服从“尖峰厚尾”的分布时,则会出现偏差。
美国著名的基金公司——桥水基金被广为赞誉的“全天候策略”,就是应用了风险平价模型的核心思想,从而达到了多元化投资,保证投资组合风险可控,进而取得更为稳健的投资收益。
四、模型的改进和拓展方向
上述的资产配置模型方法尽管在实践中得到了广泛而有效的应用,但仍有不足之处和继续改进拓展的空间。以经典的马科维兹模型为例,虽然马科维兹模型将资产配置由定型分析发展到定量分析,具有里程碑的意义,但模型仍有改进的空间。模型中的一个重要前提假设是资产风险收益服从正态分布。但由大量的真实金融市场数据表明,资产收益率的分布,服从“尖峰厚尾”的分布。正态分布的偏度为0,峰度为3,而“尖峰厚尾”则名副其实:数据的分布有一定的偏斜、不对称并且更集中。由图像直观的来说,资产的收益率出现极端值的概率要比正态分布数据出现极端值的概率更大。这说明在模型中仅仅使用收益率的一、二阶矩——期望和方差来刻画证券的风险特征是不够的,仍有剩余的有价值信息隐含在收益率数据的更高阶矩形——三、四阶矩,即偏度和峰度中。更加充分的挖掘数据中的信息对于模型的构建势必有更好的效果。
参考文献:
[1]任飞, 李金林.资产配置理论与模型综述[J].《生产力研究》,2007 (7) :140-142.
[2]管鸿禧.马科维兹资产组合选择理论评述[J].《经济学情报》,2000 (5) :56-60.
[3]龙先文,邓纯阳.对马科维兹投资组合理论的反思[J].《特区经济》, 2005 (11) :351-352.
[4]蔡文捷.基于风险平价策略的大类资产配置实证研究[J].《浙江大学》,2017.
