数学课堂教学思维过程的设计

韩旭东 郑丽杰

摘要：课堂教学中，思维过程的设计起了很大的作用，好的思维设计，不但能帮助学生形成良好知识结构，提高学习兴趣，还能最大程度的提高课堂教学效果。本文从问题的提出、概念的形成、结论的探索、方法的思考几个方面入手，对思维过程的设计进行探讨。

关键词：数学教学;思维过程;设计

过程性原则是数学学习和研究过程中的重要原则，此原则要求老师从结果出发，精心设计，将数学思维活动融入数学课堂教学中，以求学生能够按照一定的思维规律逐步进行数学思维活动，不仅能让学生形成良好的知识结构，提高学习兴趣，而且能提高课堂教学效果。

数学设计思维过程的本质就是将数学思维的主要过程“重现”出来，这里面不但包括了提出问题、形成概念，还包括了探索结论、思考方法等。下面就这几方面进行探讨。

教学的重要过程之一就是问题的提出。为此在我们的教学中要尽可能做到从学生已有的认知结构出发来全方位展示提出问题的过程。

问题提出的过程是新课引入的实质，例如在教学新课“复数的模”时，我们可以设计如下教学过程来逐步将此概念引入并让学生留下深刻的印象：

（1）在学生已掌握实数绝对值概念情况下，引导其猜想复数是否具有相类似概念？这个概念到底是什么？

（2）从几何意义来解释，实数的绝对值表示数轴上对应点到原点的距离，类似的将“复数的绝对值”理解为复平面上表示复数的对应点到原点的距离。

（3）通过类比原则可以将复数的几何意义初步引导出来，然后正式介绍这个引导的概念具体是什么？并引导提出其有一些什么性质？

下面我们可以正式开始研究“复数的模”这一课题。

这样通过两项类比，复数的模的问题就可由实数绝对值概念引出，不仅避免新旧知识的混淆，还为模的性质研究提供了方法。

以上过程在学生本身已有的知识基础上，通过猜想、类比、转化等一系列数学思维活动，不仅使问题提出得更自然，而且使学生在知识迁移这一过程中能够产生更加强烈的求知欲。

一、 概念的形成过程

强调“从定义出发”，忽视揭示概念形成过程的传统教学，使教学呈单向性，“填鸭式”的教学只能让学生被动接受知识，缺乏主动性，导致学生学习兴趣不浓。教学中要尽可能让学生参与概念形成的思维活动。概念形成方式，一般可分成：描述、揭示、概括以及构造几个类型。但对于这些类型，研究的可能性、合理性和必要性都是不可或缺的。

在“复数概念”教学中，教材通过负数在实数范围内不能开平方这一现象表明实数集的不完善，接着引入实数集需要进一步扩充的必要性。这就是提出问题的过程，那么接下来就是如何解决这一问题？

1. 回忆小学到初中的几次数集扩充过程：

自然数集→非负有理数集→有理数集→实数集

均体现了如下规律：①规定了性质的新元素的增加。 ②扩充后，不影响原数集内的主要规律。③引入扩大范围的新数集后可以解决原数集不能解决的一些问题。

2. 借鉴以上规律，引进新元素，规定：

①i2=-1。②它可与实数进行四则运算，并且原运算律仍成立。

根据规定，实数与i相乘，再将实数与所得结果相加。得到的数即为复数。而复数集就是全体复数所构成的一个集合。

接着对复数的性质作必要的举例验证，并说明以后的学习将进一步验证扩充的必要性、合理性及扩充的重大意义。

这就是复数概念的形成过程，通过这一过程，学生就不会对复数的引入感到困惑，也不会对复数的相关概念觉得突兀，同时为以后概念的深刻理解和进一步探究做了基础工作。

二、 结论的探索过程

数学结论的发现过程，大量的猜想和假设是必不可少的一部分，如要选择正确的结论需要通过直觉思维，而要在教学中突出思维过程，就必须将直觉思维放大并逐步剖析，既要不断挖掘教材中蕴含因素，还要不断挖掘结论探索过程。

在“椎体体积”的教学中，可以根据已有柱体体积公式求法作如下教学情境设计：

首先回顾推导柱体体积公式的过程：引导学生通过长方体这个特殊的柱体体积公式，同时提出“等底面积等高的两个柱体体积相等”这一结论，推导出一般柱体体积公式。

通过类比原则来猜想：是否可以用以上思路来探索椎体体积？

先考虑底面积为S，高为h的三棱锥这个特殊的椎体，如何求出它的体积？

通过联想、类比三角形面积公式的推导过程，将三角形补成平行四边形得到公式。

作以下猜想：是否可以将三棱锥通过补成三棱柱，从而得出三棱锥体积公式。

图1如何补？我们已经知道可以将三棱柱通过下列方法割成三个不同的三棱锥。如图所示：

逆向思考：以上三个三棱锥重新补成三棱柱，这样三棱锥体积公式不就可以推出了。

如果再有“等底面积等高的两个椎体体积相等”这一条件，是否就可猜想：底面积为S，高为h的棱锥的体积为V=1/3Sh。

在老师引导下，学生通过类比、联想、猜想等一系列方法，亲身经历了棱锥体积公式的探索过程，如此能够激发学生的学习热情，从而使其将知识掌握得更牢固。

三、 方法的思考过程

教材通常都是直接给出数学结论的证明，然而这些巧妙的方法是怎么想出来的？学生都是不得而知，只能死记硬背。因此，我们在教学时首先要使学生掌握下列思考问题的方法：猜想、试验、类比、联想、观察、演绎、归纳等，以使学生在具体思维过程设计时能够灵活运用。

对于“点到直线的距离公式”证明，虽然教材采用的证明方法不难，但大多数学生对图中添加的辅助线却感到困惑。要解决这个问题，我们可以设计如下过程：

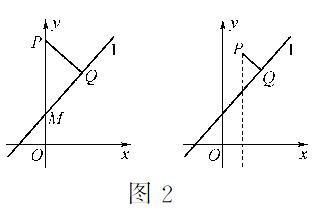
先用特殊位置思考，当点P在坐标轴y轴上时，点P到直线l的距离如何求？引导学生构建直角三角形，提出如图所示方案：d=|PQ|=|PM|cosα。

本方案采用方法是：找一直角三角形，假设确定了斜边和一已知角，便能将所求距离转化成求三角形的一条直角边，如此更清晰明了，学生也能更快地掌握。

学生解决这个特殊问题后，再回头解决原问题就简单许多。通过特殊问题的解决，可以使得一般问题得到提示，不会显得迷茫不知从何处下手：找一直线作为斜边所在的直线，构造一直角三角形。

图2如图，要构造一直角三角形，只需过P作一直线与直线l相交，就可构成直角三角形。如果任意作直线，内角就没法确定，我们能都作y轴（或x轴）平行的直线吗？引导学生作出图形，推导出点到直线的距离公式，从而使得一般性问题得以解决。

通过这样的教学，学生不仅能理解这样作辅助线的原因，而且深入研究探索还可以得到不同的解决方法。而学生在牢固掌握知识的同时，还知道了方式方法，得到了能力的发展。

如果每堂课都精心设计教学过程，那么就更能激起学生学习热情，进一步提高学生主观能动性，使得课堂效率更高。

參考文献：

[1]罗祖兵.教学思维方式：含义、构成与作用[J].教育科学研究，2008（Z1）.

[2]法鲁克.试论数学问题教学中常用的数学思维方式[J].新疆教育学院学报，2006，22（4）：124-127.

作者简介：

韩旭东，郑丽杰，江苏省宜兴市，江苏宜兴市官林中学。