平平淡淡才是真 别开生面领悟深

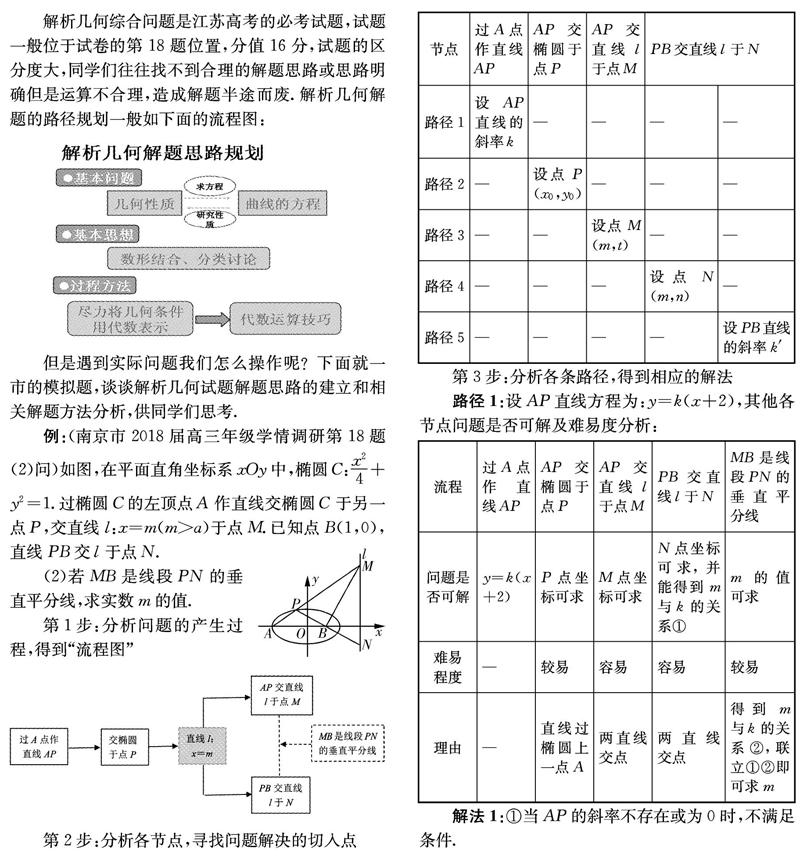
解析几何综合问题是江苏高考的必考试题，试题一般位于試卷的第18题位置，分值16分，试题的区分度大，同学们往往找不到合理的解题思路或思路明确但是运算不合理，造成解题半途而废.解析几何解题的路径规划一般如下面的流程图：

2.解题几何中的多动点问题，一直是同学们难以逾越的障碍，究其原因：“多且动”，大有牵一发而动全身的感觉，各个点都丝丝相连，环环相扣.而恰恰正是点多且动，反而给我们一个启发，多且动的点中肯定有一个“核心点”，正是这个点牵动了其他点，使其他点始终围绕这个“核心点”运动.

3.圆锥曲线综合问题，主要是找到解题切入点，优化解题过程.常用的解题策略有：①建立适当的平面直角坐标系；②设而不求，变式消元；③利用求根公式沟通坐标与参数的关系；④发掘平面几何性质，简化代数运算；⑤用函数与方程思想沟通等与不等的关系；⑥注意对特殊情形的检验和补充；⑦对于中点弦问题，通常有两种常见的处理方法，一是通过将直线与曲线方程联立，应用根与系数的关系来处理；二是应用点差法，找到直线的斜率与中点的坐标间的关系来处理.

（作者：熊如佐，江苏省东海高级中学）