小学数学与中学数学的有效衔接

黄依平

【摘 要】刚刚踏入中学门槛的学生在数学学习上存在诸多不适，有相当一部分学生出现了数学成绩下降的现象。本文对影响小学数学与中学数学课堂衔接的因素进行分析，主要从教材体系、教学方法、学生的认知发展等方面进行了比较，由此提出，应加强小学数学与中学数学课堂教学内容的衔接、课堂教学衔接应遵循的原则，并给出了促进小学数学教师与中学数学教师有效融合的建议和策略，以帮助学生顺利从小学过渡到中学。

【关键词】小学数学;课堂教学;有效衔接

一、问题的提出

从小学到初中，随着数学知识的增加、思维方式的改变、学习视野的扩展、教学教法的不同等一系列的变化，使得刚刚踏入中学门槛的学生在数学学习上存在诸多不适，有相当一部分学生出现了数学成绩下降的现象。而目前在小学与中学的课堂教学中，出现了比较严重的脱节现象，在新一轮的课程改革要求下，小学阶段与中学阶段的数学教学在教学内容、教学要求、教学方式、教学目标等方面都存在明显差距。为此，加强中小学数学课堂教学的衔接至关重要。

对中小学数学课堂教学衔接的研究，能够逐步扭转目前中学与小学数学课堂教学上的脱节现象，使中小学教师能够更加深入地了解《数学新课程标准》的教学目标和教学理念，能够为小学生进入初中后快速适应中学数学的学习搭桥铺路。

二、加强中小学数学课堂教学衔接的对策

中小学数学的知识较为丰富，要做好中小学数学的课堂教学衔接，就要对中小学数学的课堂教学内容进行分析、研究。一般认为，从小学算术到初中的代数、几何，有四个主要的知识衔接块：算术数与有理数;数与式;算术解法与代数解法;实验几何与论证几何。

（一）算术数与有理数的衔接

小学阶段学习的整数、小数、分数都是最基础的知识，属于算术数领域。而中学阶段，初一新生首先接触到的数是负数，再逐渐对数的认识扩充到了有理数域。负数似乎不难，但却扰乱了学生原有的数的观念，这实际上是一种质的飞跃，所以，做好算术数与有理数的衔接可以为中小学学生学好数学奠定基础。

1.充分解释有理数的概念

对于刚接触有理数的初一学生，教师需要清楚地解释有理数与算术数的区别，让学生了解有理数与小学的算术数相比只是增加了负分数与负整数，只有正确区分了算术数与有理数，学生才能在有理数域中进行运算。

2.清楚讲解有理数的运算法则

要让学生懂得运算前要先确定“符号”，再进行“算术数”的运算。显然学好“算术数”的运算，可以为有理数的运算奠定基础。因此，在课堂教学中，教师要让学生熟练掌握运算步骤，加强计算能力，进而使中学教师能在小学运算法则的基础上，让学生进行有理数的运算。

（二）数与式的衔接

小学生学习的主要是具体的数，初中生学习的主要是用字母表示数，而代数式是在数和表示数的字母的基础上形成的，是数的进一步拓展。初一学生学习代数时，要经历由数到代数的过渡，其实也就是学生由具体到抽象，特殊到一般的过渡，是学生学习的难点所在。因此，注意挖掘中小学数学教材本身的内在联系，如对整数与整式、分数与分式、有理数与有理式、无理数与无理式的联系进行分析和比较，弄清它们之间的区别和联系，对搞好由数到式的过渡衔接是有意义的。

在小学课堂教学中，教师在涉及到用字母表示数这一课时，不能一带而过，要注意总结所学知识中有关字母表示数的内容，让学生对其有个清楚的认识，从而为中学学习代数式打下扎实的基础。

（三）算术解法与代数解法的衔接

在中小学数学中，应用题的解法一般有两种，分别是算术解法和列方程解法，但小学生普遍倾向于使用算术解法，而中学数学则要求学生以列方程为主。小学生在解决问题时，常通过了解已知条件并进行思考，进而得出未知条件，这一个思维过程就是算术解法的思维过程。中学生在解决应用题时，往往会把未知量当做已知量，找出等量关系后再解决问题，所以往往会使用列方程的方法。从算术解法到代数解法，对学生而言是一大转变，因此，中小学教师要加强算术解法与代数解法之间的衔接。

1.注意有关解方程方法上的转变

小学教师在讲授解方程时，是依据“和”“差”“积”“商”公式中各个部分的关系来解方程的，中学教师则通过讲解等式的性质来解决方程问题，这两种解决方法思维过程不同，但实际运算步骤相同。所以，小学教师在讲解时，应注意将两种思维方式进行梳理、比较，从而让学生理解并熟练地掌握解方程的运算步骤，使学生能够明确每一步运算的依据。

2.比较算术解法与列方程解法的优缺点

在中小学课堂教学中，教师应有意识地将一些使用列方程解法更为简单的应用题作为例子，让学生比较算术解法与列方程法哪一种更为简便，让学生体会到列方程的优势，逐步增强其列方程解应用题的意识，提高其思维能力。

3.提高列方程解应用题的能力

要求列出方程，首先要找出数量关系。小学数学教师在讲解应用题时要大胆放手，让学生讨论、交流，准确找出题中的数量关系，并培养学生找数量关系的意识。中学数学教师在讲解应用题时，适时地点拨引导，让学生通过个体独立思考、小组合作互助、教师点拨指导，进而学会审题;让学生采用画图、列表等方法进行分析数量关系，进而找出等量关系、列出方程并解决问题，使之形成“观察—分析—归纳”的良好习惯，逐步提高解题能力。

（四）实验几何与论证几何的衔接

小學教材中涉及到的几何内容有：对长方形、正方形等平面几何的认识;对长方体、正方体、圆柱、圆锥等立体几何的认识，属于实验几何的范畴;而中学几何知识则涉及到有关几何图形的概念、性质以及相关的证明方法，可以归类为论证几何。从实验几何到论证几何知识的改变，要求中小学教师做好有关中小学几何知识的衔接。

1.注意几何语言的过渡

几何语言是学习几何知识的基础，只有学好了几何语言，才能准确掌握几何知识。在小数数学教学时，教师应注意准确叙述几何语言。如讲解点到线的距离时，应强调“点到直线的垂直距离”，注意纠正学生“直线到点的距离”的错误说法。初中教师则要注意对几何符号语言的讲解，注意∥、⊥、≌等几何符号的引入，应在学生充分理解两条直线平行、两条直线相互垂直、两个三角形相似等相关概念时，再引入几何符号语言的知识。

2.注重对学生论证能力的培养

初中数学重视学生的几何论证能力，所以，小学数学教师在讲解几何知识时，应该多问些“为什么”，让学生在掌握知识的同时能够进行思考;初中教师则要在小学所获得的知识的基础上，进行论证讲解。

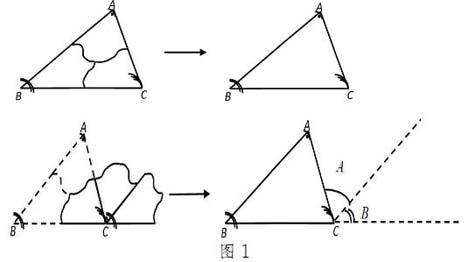
例：如图1所示，在讲解有关三角形内角和的知识时，小学教师可以通过实物让学生拼一拼、剪一剪，并能够讨论得出三角形内角和等于180°的结论，注意让学生说出原因和结果;而初中教师则可以在小学生的思维的基础上进行引导、提示，从而让学生能够通过论证的方法得出结论。

总之，从20世纪中国实行科教兴国以来，越来越多的专家学者开始注重对教育的研究，中小学数学课堂衔接研究也引起了广泛的关注。希望本研究能够对部分中小学教师有一些帮助与启发。当然，要解决学生难以适应中小学数学知识变化的问题，单从教师课堂教学方面进行研究是不够的，笔者希望通过与更多学者的交流，进一步对这一问题展开研究，共同促进中小学生数学成绩的提高。

【参考文献】

[1]邓国尧.加强中小学数学教学衔接的探索[J].现代教育论丛，1993.6：43-45

[2]黄豪杰，戴振祥.中小学数学教学衔接问题的研究[J].宁波教育学院学报，2009.11：112-115

[3]吕金林.谈中小学数学教学的衔接[J].延安教育学院学报，1994.13：42-45