论“小题大做”——基于数学抽象能力培养的例题设计与教学

数学抽象包含数学概念、命题、方法和体系的抽象，是重要的数学核心素养，在数学课堂例题教学中合理地设计数学抽象活动，积累数学抽象活动经验，这是基于数学核心素养的教学设计的必然要求，也是追求数学育人的必然要求.但是目前课堂教学“三多三少：学生做得多，思考得少；现成资料多，自主设计少；教师讲得多，提炼得少”的现象较为普遍.一些公开课上培养核心素养的环节被认为是不可复制的.这样的矛盾如何破解？我们不妨“小题大做”，即从课堂例题教学设计的小处入手，在培养核心素养的大处立意.

一、概念性例题“小题大做”，用充分的数学过程完成概念的抽象

“学生做得多，思考得少”在概念教学中尤为突出，概念的形成和同化不是一两句话的问题，更不能用做题来替代，只有在充分的数学经历之后的数学抽象才是有价值的、高质量的概念抽象.在概念教学中，应精心设计例题，带领学生从具体问题出发，抽象出一类数学现象的共同属性或本质属性，从而形成数学概念，并通过表达、判断、应用等多种途径，完成知识迁移、误区矫正，使最关键的“数学抽象”找到强有力的过程支撑，让学生的数学抽象能力在递进问题的探索中得到发展，思维在逐层探究中得以丰富.

案例1：在浙教版七上“3.1平方根”这节课中，在给出已知正方形边长求面积、已知正方形面积求边长的一些实例的基础上，与学生共同概括出平方根定义以后，教师给出：

生1：我认为49的平方根是±7.

师：用规范的格式来叙述.

生1：因为±7的平方等于49，所以49的平方根是±7.

师：0的平方根呢？

生2：0乘以任何数都得0，0乘以0也得0.

师：这个答案不怎么行.

生3：因为±0的平方等于0，所以0的平方根是0.

生4：不对，0既不是正数也不是负数.

师：0的前面不加性质符号.

师：刚才我们从互逆运算的角度，先进行平方运算，再逆过来进行开平方运算.这里我有几个问题：（1）一个正数有几个平方根？它们有怎样的数量关系？（2）0的平方根是什么？（3）负数有几个平方根？

生5：一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根.

生6：我不同意，正数并不一定有平方根，如10，没有一个数的平方是10.

师：如果正方形的面积为10，那么它的边长是多少？这样的边长一定存在啊.

师：你已经预习过课本了，我们今天就来学习这个符号.

师：那么负数呢？请说说你的理由.

生8：x2=a中，如果x是正数，两个正数相乘得正数a；如果x是负数，两个负数相乘也得正数a，所以负数没有平方根.

生9：一个数的偶次幂均为非负数，举个例子：（±4）2=16，一个数的偶次幂不可能是负数，所以负数没有平方根.

师生共同总结：一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根.

师：刚才生6的问题非常好，我们熟悉的乘法表中没有这样的公式：几几得10，所以必须有个新的符号，首先让我们来了解“”产生、演变的历史……

例1很短小，但是整个例题教学过程很细致.学生表达不规范时，教师耐心包容地解释；不同学生有不同的观点时，教师从不同的层次进行解释；学生有思维漏洞时，教师及时从不同的维度打补丁，并且反复强调“平方—开方”是互逆运算，强化新概念的逻辑起点和逻辑顺序，让学生感受学习平方根的必要性和思考的合理性.数学课堂教学应该是以这种“逻辑推理”的姿态影响着学生，让学生一次次纠正自己的漏洞，在行动和思考中变得周全，学生就是这样成长变化的.这些问题看起来很琐碎，但是，教学的目的就是教会学生思考，学会学习.

概念课的例题设计和教学应该揭示概念生成的生活背景，了解概念产生的必要性与合理性，让学生经历对概念由感性到理性的认识过程，通过典型的实例引导学生对概念的属性进行分析、比较，充分讨论、理解后归纳出共同属性.一定要让学生有充分的过程性体验，让学生以“发现者”角色经历概念的发现过程，辅助学生对知识进行同化与顺化，促进学生认知水平、抽象能力的发展.

二、相关性例题“小题大做”，用双向聚敛思维完成命题、方法的抽象

“现成资料多，自主设计少”，显然数学命题、模型要比数学题目少，数学思想方法比数学命题、题型要少.课堂中应经常将众多相关、相似的题目，从纵向、横向两个思维方向进行组织，运用聚敛思维直达本质，寻找出一类问题最好的解决方法，不断反思和总结，积累抽象活动经验，使学生学会学习，从而大幅度减少“刷题”的数量.

案例2：人教版八上数学P17第9题：如图1，∠1=∠2，∠3=∠4，∠A=100°，求x的值.

图1

在“三角形角平分线的专题复习”这节课中，教师针对此题进行了基于纵、横两个思维方向，指向抽象水平三个层次的设计.

环节1：基于横向思维设计，指向抽象水平一.

课堂上师生充分交流了各种解题方法.学生的解法主要有三种，方法1是将∠ABC+∠ACB看成整体，分步计算.方法2是分别由△ABC、△GBC的内角和列方程组，消元求解.方法3是利用基本图形结论.师生小结后，教师抛出了3个变式.

变式1：如图2，BG平分∠ABC，CG平分∠ACB，探究∠BGC与∠A的数量关系.

变式2：如图3，BO平分∠DBC，CO平分∠BCE，探究∠A与∠O的数量关系.

变式3：如图4，BH平分∠ABC，CH平分∠ACD，探究∠A与∠H的数量关系.

图2

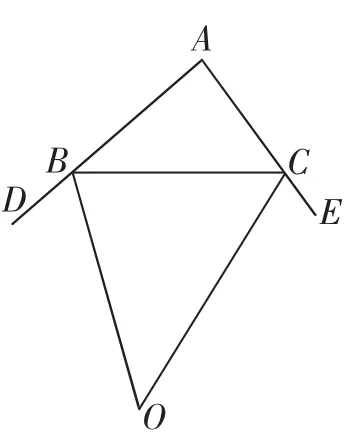
图3

从原题到变式1，从特殊到一般，学生唾手可得.对于变式2、3，三种方法均能迁移.学生用的最多的是方法1，但是渐显颓势，部分学生表达不规范、思路不清晰.而方法3，基本图形只有在长期训练下才能在较短的时间内被发现.几何问题代数化在几何中探究数量关系时是通法，用方法2始终清晰明了，教师重点引导，优选方法，归纳结论.

这样的设计让学生在具体的数学情境中，通过从特殊到一般，归纳并形成简单的数学命题，用规范的数学语言表达推理和论证，能够在相似、相关的问题中感悟问题的通性和通法.

环节2：基于纵向思维设计，指向抽象水平二.

教师引导学生观察变式1、2、3的共同点，启发学生运用化归思想，寻找新的解题方法.如在变式3中，学生作∠ACB的平分线交HB于点G，这时便将问题化归为变，更快、更简洁地得出结论，变式2亦是如此.为什么利用化归思想能够如此快捷呢？说明彼此之间必然存在内在联系.因此师生把重点放在探寻三者之间的内在联系上.学生大胆猜测，而后叠合图形（如图5），找出问题的本源是三个变式都是图5的一个部分.师生共同提炼模型并总结：相似的问题、相关的问题可以运用类比、化归思想，并善于用联系的眼光、整体的方法去反思解题.

图5

在此基础上，教师从纵向设问，从角平分线变化到角的n等分线时，结论是否发生改变？学生沿用刚才的方法得出结论.

这样的设计让学生能够理解和构建相关问题之间的联系，抽象数学模型，提炼出解决一类问题的数学方法，理解其中的数学思想，将已知数学命题推广到更加一般的情形.

环节3：基于横向思维设计，指向抽象水平三.

教师进一步问学生：你想进一步探究相关的哪些问题？学生们纷纷提出四边形、六边形甚至n边形，并一起合作，模仿环节1、2进行进一步的研究，验证环节2中发现的结论和方法在四边形中是否成立，并根据这些结论和方法快捷地解决一些复杂的问题.

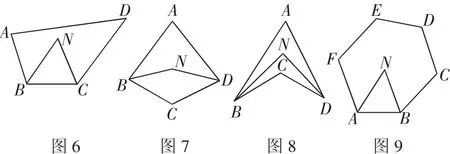
例2 如图6，四边形ABCD的内角∠ABC、∠BCD的角平分线交于点N，探索∠A、∠D与∠N之间的数量关系.

变式1：如图7，四边形ABCD的内角∠ABC、∠ADC的角平分线交于点N，探索∠N与∠A、∠C之间的数量关系.

变式2：如图8，凹四边形ABCD的内角∠ABC、∠ADC的角平分线交于点N，求∠N与∠A、∠C之间的数量关系.

变式3：如图9，在六边形ABCDEF中，∠FAB、∠ABC的角平分线交于点N，求∠N与∠C、∠D、∠E、∠F之间的数量关系.

环节3让学生能够在有序多级的情境中抽象出数学模型，使之更具普适性，针对具体问题运用或创造数学方法解决问题，并进行高度概括.

这节课以一个课本题为载体，将问题从横、纵两方面加以探究，通过问题间的相关性、相似性，循序渐进将问题迁移，学生从特殊到一般，进行合情猜想、类比、化归，层层递进，通过“小题大做”，系统有序地设计抽象过程的不同阶段的活动，让学生充分有序地经历数学抽象过程，通过及时反思和迁移，积累了数学抽象活动经验.

三、领域性例题“小题大做”，借整体性设计完成系统的抽象

“教师讲得多，提炼得少”，教师往往就题讲题，但数学知识系统之间往往是有关联的，对于例题设计和教学，考虑不同的局部知识系统之间的关联，应把已经建立的知识系统及其学习经验应用于新的内容的学习.

案例3：在函数学习中，我们从一次函数、反比例函数，到二次函数，应研究研究函数过程的共性，发现研究函数性质的共性，抽象研究函数的思路和方法，类比研究函数的思路和方法，确定函数领域的共同逻辑基础，从系统性的角度抽象学习的过程，并程序化（如图10），为后续的函数学习打下坚实的基础.如例3，中考数学经常考新定义型函数问题：

图10

（1）若矩形的两边长分别是2和3，当这两边长分别增加x和y后，得到的新矩形的面积为8，求y与x之间的函数关系式，并判断这个函数是否为“奇特函数”.

（2）如图11，在平面直角坐标系中，点O为原点，矩形OABC的顶点A、C的坐标分别为（9，0）、（0，3）.点D是OA的中点，连接OB、CD交于点E，“奇特函数”y=的图像经过B、E两点.

图11

向上平移_______个单位就可得到①中所得“奇特函数”的图像.过线段BE的中点M的一条直线l与这个“奇特函数”的图像交于P、Q两点，若以B、E、P、Q为顶点组成的四边形的面积为，请直接写出点P的坐标.

学生如果通过与研究函数的思想方法类比，从整体到部分、从粗略到精细、从定性到定量，运用函数问题研究的常用策略：（1）研究函数按图像-性质-应用的途径；（2）先运用特例研究，再归纳一般；（3）画图，归纳对称性、最值、特殊点、增减性等性质，必定可提升宏观的数学视野，不会再对此类问题心存恐惧.

因此，凡是能提升学生学习效率，提升学习和研究数学的水平，提升数学思维能力，发展核心素养的例题，就有必要“小题大做”.反之，应尽量避免.

在浙教版八上“5.1常量和变量”这节课中，有这样一道习题：

圆周长C与圆的半径r之间的关系式是C=2πr，其中常量是_____，变量是_____.

这里的常量是2π还是2、π呢？要不要在课堂上谈论呢？概念是思维的基本单位，为什么要学常量和变量？“5.1常量和变量”为什么是函数的起始课？课标是这样叙述的：“探索简单实例中的数量关系和变化规律，了解常量和变量的意义.”常量和变量是为函数学习所准备的概念，它服务于函数，离开具体函数谈常量和变量是毫无意义的.因此结合大量的生活中的、数学中的问题，让学生站在函数视角研究常量、变量，即在充分体验现实生活、数学问题、其他学科中各种量与量之间的变化规律和数量关系中，引导学生抽象出变量和常量的概念，才是本节课的重中之重.不能抛开核心素养的培养，纠结于这些细碎的有争议的问题，那真的是小题大做了.

1.吴增生.数学抽象的认知机制及其教学策略［J］.中国数学教育，2017（4）.