基于数学史的新知引入课例分析

◎ 陈晏蓉 汪晓勤

实践表明，HPM视角下的数学教学（即融入数学史的数学教学）不仅对学生的学习产生了积极的影响，而且也丰富和完善了教师面向教学的数学知识（MKT），其中包括内容与教学知识（KCT）。引入是课堂教学的主要环节之一，为整节课的知识传授做铺垫。巧妙的课堂引入可以在短时间内吸引学生的注意力，激发他们的学习动机，并引领他们主动参与到课堂中。因此，关于如何引入新知是KCT的重要组成部分。

早在20世纪50年代，美国学者琼斯（P. S. Jones）就曾指出，数学史为教师提供了引入新课的话题，也为学生提供了发现新概念或新思想的方法。［1］当代也有数学教育研究者提出，数学史丰富了教师的背景知识，教师通过数学史可以确定引入数学新知的动机。［1］

近年来，越来越多的一线教师对HPM视角下的数学教学产生兴趣，相关的课例（本文称之为“HPM课例”）日益增多。我们关心的是，在这些课例中，教师是如何引入新知的？数学史在新知引入中是否起作用？有关学者的上述论断是否可以得到印证？

为了回答上述问题，我们对部分高中HPM课例进行了考察和分析，试图为HPM课例开发与实践提供参考。

一、课例选取

我们选取2007—2016年10年间发表的11个HPM课例［2—13］作为研究对象。这些课例所属课型均为新授课，具体情况如下：6个代数主题，2个三角学主题，2个解析几何主题和1个微积分主题。大多数课例是由大学数学教育研究人员和中学数学教师合作开发而成的，课例研究的流程如图1所示。［1］实践中，第二个环节“研讨与设计”和第三个环节“实施与评价”之间往往会经历多次循环。

图1 HPM课例研究的流程

在已经开发的高中HPM课例中，并不是每一个课例都在导入环节融入了数学史，本文中的课例选择标准是新知引入与数学史密切相关。

二、新知引入的类型

数学教学中的新知引入方法很多，不同的作者都曾给出过各自的分类方法，一些作者还提到利用数学史料来引入［13—14］，但对于如何利用数学史料来引入，迄今很少有人作出进一步的探讨。通过分析，发现在本文所考察的11个HPM课例中，7个采用了问题引入，2个采用了故事引入，1个采用了演示引入，1个采用了实例引入。

（一）问题引入

问题引入是通过让学生解决一个或多个具体的问题，在解决问题的过程中引入新知。

在课例“对数”［2］的导入环节，教师由计算天文学中一光年的大小（299792.468×31536000）的问题引入，让学生从中体会运算之繁，了解16—17世纪天文学家在研究天体运行规律时要耗费大量的时间进行数据运算。接着，通过等差数列和等比数列之间的对应关系，体会数表的效用与局限，由此引入对数的概念。

在课例“两角和与差的三角公式”［3］中，教师根据古希腊数学家帕普斯（Pappus）的和角公式几何模型，设计一系列问题。

问题1：图2（a）、图2（b）展示的是两角和的正弦公式的证明方法，你能说明其证明过程吗？

图2（a）

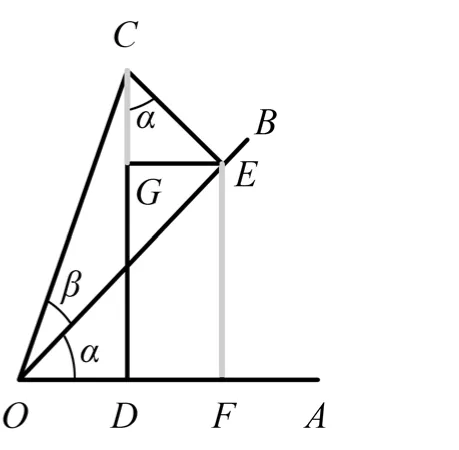
图2（b）

图3（a）

图 3（b）

问题2：参考了上述证法，再看看图3（a）、图3（b），能得到什么结论呢？

问题3：你能利用问题1与问题2的结果计算出sin75°与cos75°的值吗？

问题 4：求 sin25°cos65°+cos25°sin65°与cos40°cos35°－cos40°sin35° 的值。

问题5：问题1和2中的公式是否对任意角α与β都成立？

在课例“正弦定理”［4］中，教师以流星的测量问题引入。如图4所示，O为地球球心，A、B为观测者所在位置，观测者相距500km，AD、BD为地平线，交于D点，从A、B观测流星 C，仰角分别为 α=23.2°、β=44.3°，求流星与两位观测者的距离分别是多少。而后，教师通过引导学生将实际问题抽象为数学问题，即在三角形中，已知两角及所夹边，求其余两边的问题。从而引入本节课的主题。

流星测量引入是根据10世纪阿拉伯天文学家阿尔·库希（al-Kuhi）的流星测量方案改编而成的。

在课例“均值不等式”［5］中，教师首先介绍了《几何原本》第六卷命题13：求作两条已知线段的比例中项（即几何中项）。欧几里得的作法如图5所示。设AC、CB是两条已知线段，它们在同一条直线上，以AB为直径作半圆ADB，在点C处作AB的垂线CD，交半圆周于D，则CD就是所求的几何中项。

图4

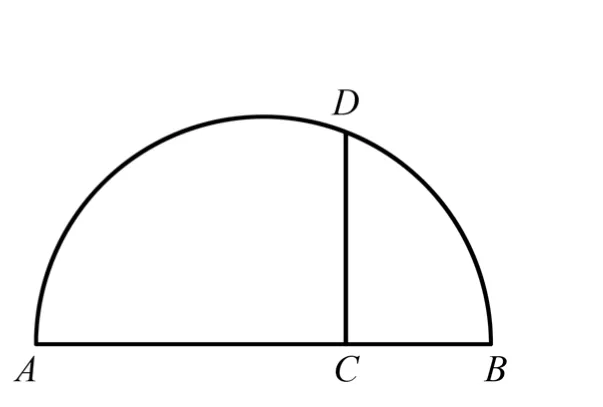
图5

据此，教师设计了以下问题串。

问题1：结合图5，证明CD是AC和CB的几何中项。

问题2：在图5中作出AC和CB的算术中项，然后比较算术中项和几何中项的大小。

问题4：正数a、b的几何平均数和算术平均数何时相等？请结合图5加以说明。

在课例“曲线与方程”［6］中，教师通过古希腊数学家阿波罗尼奥斯（Apollonius）的“二线”和“三线”轨迹问题引入：求到两条相互垂直的定直线距离相等的动点轨迹以及到两条平行线距离乘积与到第三条与它们垂直的直线距离的平方相等的动点轨迹。阿波罗尼奥斯原问题中，直线的位置关系是任意的，并且距离之比或距离乘积与距离平方之比为任意常数，教师对其进行了特殊化的处理。

在课例“数系扩充与复数的引入”［7］的开始，教师提出一个具体情景中的问题：要用20分米长的彩带制作一个面积为24平方分米的长方形框架，应该如何确定长和宽？学生通过求解得出长为6分米，宽为4分米。接着，教师给出卡丹（G. Cardan）在《大术》中提出的问题：“和为10，乘积为40的两数分别是多少？”教师由卡丹的解法引入虚数的概念。

在课例“导数的几何意义”［8］中，教师通过三个具体的问题引入：

·我们很容易画出平面的反射光线，那么在曲面上光是如何反射的呢？

·已知某物体的运行轨迹，我们如何确定它的速度方向呢？

·我们很容易确定斜坡的坡度，但拱桥的坡度又如何确定呢？

三个问题分别对应 17 世纪数学家研究过的三大问题——光在曲面上的反射问题、曲线运动的速度方向问题以及曲线的夹角问题，正是这三大问题促使数学家对曲线的切线进行研究。此处教师巧妙地运用了数学史。

（二）故事引入

所谓故事引入，即将数学史上有关知识的发生背景以故事的形式讲述给学生，以此来引入新知。

在课例“函数的零点”［9］中，教师由以下故事引入：在神圣罗马帝国时期，人们经常在公共场所举办数学竞赛。比赛常常吸引众多的观众，其盛大景况堪与今天的明星演唱会相媲美。神圣罗马帝国皇帝腓特烈二世也是个数学迷。有一次，他举办了一场宫廷数学竞赛，其中一道竞赛题是求三次方程x3+2x2+10x=20的根。来自比萨的大数学家斐波那契（L. Fibonacci）成功地获得了它的近似解，并精确到了小数点之后的6位数字。斐波那契赢得了比赛，深受皇帝的赞赏。教师进而引导学生作出相应的三次函数图像，寻找方程根与函数图像之间的关系。

在课例“递推数列”［10］中，教师以古代印度的故事引入：在世界中心贝那拉斯的圣庙里，一块黄铜板上插着三根宝石针。梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣按照下面的法则移动这些金片：一次只移动一片，不管哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界将在一阵霹雳声中毁灭，而梵天塔、宇宙和众生也都将同归于尽。由此引入汉诺塔游戏。

（三）演示引入

演示引入即教师设计具有启发性和趣味性的实验活动或是使用自备的教具、动态课件，通过实际操作来引入新知。

在课例“抛物线概念”［11］中，教师借鉴古希腊数学家发现圆锥曲线的过程，通过圆锥模型，展示了椭圆和双曲线的截法，然后引导学生思考：用平行于母线的平面去截圆锥，能截出什么图形？教师用实物（实际上是一个抛物面）来拟合圆锥的截口，然后将该实物与二次函数的图像进行比较，从而引出抛物线。

（四）实例引入

所谓“实例引入”，即将历史上与本课所教内容有关的具体例子用于引入部分。

在课例“数列概念”［12］中，教师以两河流域泥版（公元前7世纪）上记录的一张月相变化表（见表1）作为第一个实例来引入数列概念：将满月分成240部分，则从新月开始，每天的月相变化情况见表1。该表呈现的其实是一个月相数列：前5项构成公比为2的等比数列，第6—15项构成公差为16的等差数列。

三、基于数学史的新知引入的特点

表1 月相变化表

M·克莱因（M. Kline）曾提出四个数学课程原理——兴趣原理、动机原理、直观原理和文化原理［15］，而波利亚（G. Pólya）则提出三个数学教学原理——主动学习原理、最佳动机原理和阶段序进原理［16］。根据上述原理，结合课堂引入的功能，我们认为，一种理想的新知引入方式至少需要具备以下基本特征：

（1）可学性，即引入建立在学生已有知识基础之上，易于为学生所理解；

（2）有效性，即引入能够有效地揭示新知的必要性，激发学生的学习动机；

（3）关联性，即引入能够为后面的相关知识服务；

（4）趣味性，即引入能够激发学生学习新知的兴趣。

根据上述特点，我们对各HPM课例中的引入方式特征进行分析。

“对数”是人教版高中数学必修1中的内容，教科书通过人口增长模型y=13×1.01x来引入，符合知识的逻辑顺序，但不符合历史顺序。对数的发明源于数学家简化大数乘除运算的动机，在历史上，其主要功能就是简化计算。发明对数的主要方法是利用等差和等比数列之间的对应关系，事实上，“对数”中的“对”，就是“对应”的意思。HPM课例试图通过历史的重构，有效地揭示了对数的必要性，为对数的运算法则埋下伏笔，具备有效性、关联性和趣味性特点。

“函数的零点与方程的根”是人教版高中数学必修1中的内容，教科书由二次函数图像与x轴交点和一元二次方根之间的关系，引出函数的零点概念。学生对于一元二次方程的解法已经耳熟能详，为何还要通过二次函数的图像来解方程？HPM课例则通过斐波那契求解三次方程的故事引入，学生不了解三次方程的解法，通过作图发现三次方程的根与函数图像之间的关系，更能激发学生的学习动机和兴趣，因而满足有效性、关联性和趣味性特点，但可学性上不如教科书。

“两角和差的三角公式”是人教版高中数学必修4中的内容，教科书由电视发射塔的高度测量引入，贴近生活实际，体现了新知的必要性。HPM课例中由帕普斯和角公式几何模型引入，直接为和角公式的推导服务，具备关联性特点，但未能体现有效性。

“正弦定理”是人教版高中数学必修5中的内容，教科书由直角三角形三边与三角的数量关系引入。HPM课例中由历史上流星测量问题的引入，揭示了正弦定理的必要性，更具有效性和趣味性。

“数列的概念”是人教版高中数学必修5中的内容，教科书由毕达哥拉斯形数引入，是少数运用数学史的典型例子之一。形数突出了数列中序的特征，也为数列通项公式概念做好铺垫，但未能有效地揭示数列的必要性。HPM课例运用两河流域月相表，反映了数列知识与现实生活的密切联系，从而凸显新知的必要性，具备有效性、趣味性特点。但由于该数列的通项公式不易导出，因而在关联性上不如毕达哥拉斯形数。

“递推数列”是人教版高中数学必修5中的内容，教科书直接通过几个递推数列的例子来引入，学生感到比较突兀。HPM课例则通过汉诺塔的故事引出一个游戏，从操作中得出递推数列，寓教于乐，体现了可学性、趣味性、有效性和关联性。

“均值不等式”是人教版高中数学必修5中的内容，教科书采用第24届国际数学大会会标引入，融入了数学史元素，但更适用于不等式a2+b2≥2ab。HPM课例由《几何原本》第六卷命题13引入，更适用于均值不等式且有助于问题串的设计以及均值不等式链的建立，在关联性上更胜一筹。两种引入在有效性上均体现不够。

“曲线与方程”是人教版高中数学选修2-1中的内容，教科书通过平面直角坐标系中平分一三象限的直线方程y=x以及圆的方程，建立曲线与方程之间的关系，该引入建立在学生学过的直线和圆的基础上，具有可学性的特点，但在有效性上有所欠缺。HPM课例则再现了阿波罗尼奥斯的“二线”轨迹问题和“三线”轨迹问题，学生用原有几何知识可以解决前者，但难以解决后者，从而感受到几何方法的局限性与解析方法的必要性，因而既体现了可学性，也体现了有效性。

“抛物线的定义与方程”是人教版高中数学选修2-1中的内容，教科书直接通过对二次函数图像的思考以及运用《几何画板》作图引出本节内容，几何画板的动态演示让学生对于抛物线有一个直观的认知；HPM课例则通过实物模型的展示，再现了数学史上抛物线的发现过程，解决了“为什么抛物线属于圆锥曲线”以及抛物线焦点的来源问题，体现了有效性、关联性和趣味性的特点。

“数系的扩充与复数的引入”是人教版高中数学选修2-2中的内容，教科书通过方程x2+1=0引入，符合数系扩充的逻辑顺序。在初中阶段，学生已经习惯于“一个数的平方为正数”以及“方程允许无解”这样的观念。为什么一个方程非要有解不可呢？教科书的引入虽然直接、快速，但未能有效地解决虚数概念必要性问题。HPM课例则通过卡丹问题，让学生看到“两个数的和为实数，但这两个数却都不是实数”的事实，从而引发认知冲突，有效地揭示了新知的必要性。

表2 各HPM课例的新知引入特点

“导数的几何意义”是人教版高中数学选修2-2的内容，教科书由切线的动态形成过程引入，缺乏必要的铺垫。HPM课例借鉴历史，通过三个现实问题——“光在曲面上的反射”“曲线运动的速度方向”和“拱桥的坡度”引入，揭示切线研究的必要性，以此激发学生的学习动机。

表2总结了各课例中新知引入的基本特征。由表2可知，绝大多数HPM课例的新知引入都具备可学性、有效性和关联性特点。虽然一些课例在新知引入上也注重趣味性，但鉴于高中生（特别是数学基础较好的学生）的特点，一些教师主要关注数学史对学生认知上而非情感上的助益，因而引入的趣味性不足。

四 、结语

综上所述，我们所考察的11个HPM课例在新知引入中主要采用了问题引入、故事引入、演示引入和实例引入这四种方式，其中，问题引入方法采用得最多。通过数学史的融入，多数课例的引入能够有效地揭示新知的必要性，体现“知识之谐”，从而激发学生的学习动机；同时，也能满足通常的引入所应具备的可学性和关联性特点。数学史在为一线教师提供新知引入的素材的同时，也帮助教师更好地理解新知发生的动因，从而设计出更合理、更有效的引入。因此，HPM课例印证了本文引言部分所提及的数学史的价值。我们有理由相信，HPM课例中的新知引入设计为现行教科书提供了有益的补充。

另一方面，部分HPM课例的引入未能兼顾四种特点，因而在数学史料的选择、裁剪和加工上，还有很大的完善空间。此外，HPM课例的设计和实施需要建立在对教科书的深入理解之上。

［1］ 汪晓勤. HPM：数学史与数学教育［M］. 北京：科学出版社，2017.

［2］ 金惠萍，王芳. HPM视角下的对数概念教学［J］.教育研究与评论（中学教育教学），2014（9）：28-34.

［3］ 张小明. 两角和差的三角公式推导——数学史融入数学教学的案例研究［J］. 数学教学，2007（2）：42-44.

［4］ 张筱瑜,汪晓勤. “正弦定理”:用历史拓思维、润情感［J］. 教育研究与评论（中学教育教学），2015（6）：21-25.

［5］ 张小明. 均值不等式的 HPM 学习单设计［J］. 中学数学教学参考（高中版），2012（10）：68-70.

［6］ 石和飞. “曲线与方程”：用古希腊轨迹问题串联［J］. 教育研究与评论（中学教育教学），2016（3）：52-56.

［7］ 方国青，王芳. HPM视角下“数系的扩充与复数的引入”课例研究［J］. 数学教学，2013（4）：4-29.

［8］ 王芳，汪晓勤. HPM视角下“导数几何意义”的教学［J］. 数学教育学报，2012，21(5)：57-60.

［9］ 陈飞. “函数的零点”:用历史故事和问题激发动机［J］. 教育研究与评论（中学教育教学），2015（12）：28-31.

［10］ 李玲. “递推数列”:从汉诺塔游戏出发［J］. 教育研究与评论（中学教育教学），2015（9）：19-23.

［11］ 徐超. 抛物线概念教学：重构数学史［J］. 教育研究与评论，2015（8）：26-31.

［12］ 李玲，汪晓勤. 数列概念：通过历史体现“奇、趣、本、用”［J］. 教育研究与评论（中学教育教学），2016（4）：61-65.

［13］ 张守波.浅谈中学数学教学导入新课的方法.数学通报，1996，35（1）：1-2.

［14］ 于鸿丽.数学课堂教学的导入技能［J］.中学数学教学参考，2007（1-2）：10-12.

［15］ Kline M. The ancients versus the moderns：a new battle of the books［J］. Mathematics Teacher，1958，51（6）：418-427.

［16］ Pólya G. Mathematical Discovery［M］. New York：John Wiley & Sons，1965：132-133.