弹载器件的过载时间累积效应研究

钱立志， 蒋滨安， 宁全利， 李 俊,2

(1. 陆军军官学院 高过载弹药制导控制与信息感知实验室， 合肥 230031; 2. 陆军军官学院 二系， 合肥 230031)

火炮发射环境下弹载器件的动态响应研究是弹载器件抗高过载机理研究中一项重要内容，由于火炮发射时，弹丸在膛内的运动时间通常在几毫秒到十几毫秒之间，弹载器件随同弹丸承受峰值达上万g的高过载。国内外大量的研究实验表明[1]：同样过载峰值条件下，采用SHPB(Split Hopkinson Pressure Bar)冲击实验台测试时，弹载器件完好，但在火炮发射环境下，弹载器件则易损坏，原因在于过载持续时间的不同，即在长时间的持续外载作用下，作用于弹载器件上的应力相比短时间的外载要明显增大，测试器件也更易损坏，也即过载存在着时间累积效应。

有关过载时间累积效应对弹载器件抗过载能力的影响，国内外相关工程技术人员从结构上采取很多手段，解决了弹载器件在不同高过载环境下的使用问题。但对该效应的形成机理及对弹载器件的影响规律研究相对较少。文献[2]总结了近年来动态冲击实验运用与发展，提供了实验设计基础；文献[3-4]运用泡沫金属作为减载组件，通过仿真实验和理论计算获得了弹载设备侵彻过程中的过载时程曲线，对弹载器件抗高过载机理进行了研究；文献[5]通过冲击实验台对所选弹载器件进行反复冲击测试，研究了过载时间累积效应对弹载器件的影响规律，得到了计算弹载器件可承受最大过载的工程估算模型；文献[6] 研究了在过载持续时间较长情况下、作用于弹载器件上的应力计算方法，建立了基于过载时间累积的简化理论分析模型。本文以某型特种弹所用弹载光电器件及其减载组件为例，运用数值计算方法，从理论上分析弹载器件的过载时间累积效应形成机理，并通过Hopkinson压杆实验，验证理论计算方法的正确性，为不同火炮发射过载环境下弹载器件的抗高过载设计、应用提供理论分析和方法参考。

1 理论模型的建立与过载时间累积效应形成机理研究

研究所用的弹载器件及其减载组件在弹内装配结构如图1所示，弹载器件为某型特种弹装配的光学镜头，镜头旋拧在由铝合金制成的固定座上，减载组件采用7片内心中空的圆形橡胶垫叠合组成。镜头及其固定座、减载组件置于铝质套筒内，为防止减载组件反弹引起的反向冲击，在镜头固定座上方加装一片缓冲垫，通过环形扣板施加一定的预紧力予以固定[7]。

图1 弹载器件及其减载组件结构图Fig.1 The structure of projectile-based device with load-reliving subassembly

套筒底部与弹体固联，在弹丸发射时，随同弹体一起做刚性运动。加装减载组件的弹载器件在弹体内部装配结构如图2所示。

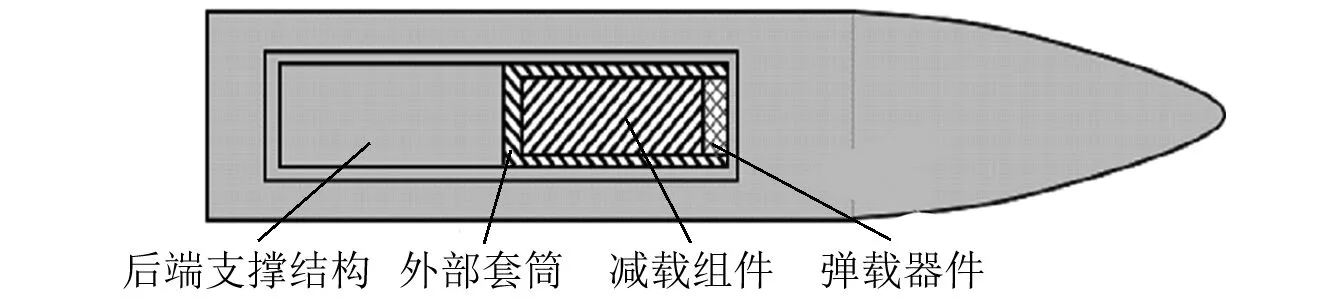
图2 弹体内部减载结构图Fig.2 The structure of internal bomb

根据图2，将弹载器件及其减载组件结构简化为图3所示的理论模型，A、B、C分别表示后端支撑结构、减载组件及其弹载器件，外载σ(t)为外加载荷。

由于B、C是一体安装，为了简化计算，可将B的等效形变参量视为弹载器件与减载组件的形变参量，将C等效屈服极限视为弹载器件与减载组件的屈服极限，用这样就可以解耦弹载器件与减载组件复杂的作用关系。

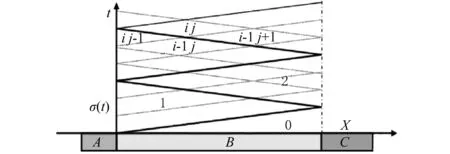
图3 弹载器件内应力波传播特征线Fig.3 The characteristic line of stress wave in projectile-based device

由于减载组件是橡胶材料，而橡胶材料在高过载环境下呈黏弹性特性，可以采用动力学守恒方程和ZWT非线性黏弹性本构方程[8]来描述黏弹性材料在高过载环境下的动力学过程。

(1)连续方程

(1)

(2)运动方程

(2)

(3)本构方程

(3)

式中：σe=Eε+αε2+βε3;E、G表征减载组件材料的弹性变形能力;ρB为B的密度;α、β表征构成减载组件材料的非线性关联度;θ为松弛时间;σ为应力;ε为应变;其中，E、G、α、β和θ是应变率的函数[9]。

根据应力波传播特点，可以采用特征线将图3所示的X-t平面离散成若干个计算区域，区域编号为0，11，12，13，…，ij。根据特征线相容关系，运用差分方法，可将式(1)～式(3)改写为差分形式

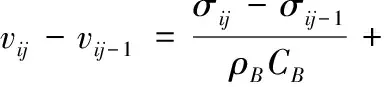
(4)

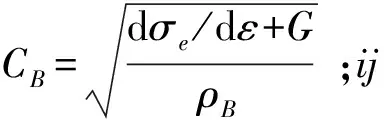
2 理论模型的实验验证

SHPB压杆冲击实验是用来测量材料动态本构关系的重要试验手段，本文所研究的弹载器件和减载组件在实际装配条件下是一体封装，在SHPB压杆冲击实验时，可视为整体当作被测试件，实验状态如图4所示，测试方法按照参考文献[10]进行。

表1是SHPB压杆冲击实验相关部件结构参数，表2是依据实验得到的被测试件动态本构关系参数。

将表1和表2中有关参数带入方程式(4)，输入应力按照SHPB压杆冲击实验得到的实测数据，计算得到作用于弹载器件的理论输出应力和SHPB压杆冲击实验得到的实际输出应力对比见图5和表3。

图4 SHPB冲击实验装配图Fig.4 The assembly of SHPB test

表1 SHPB冲击实验参数

表2 SHPB环境下被测试件的动态本构参数

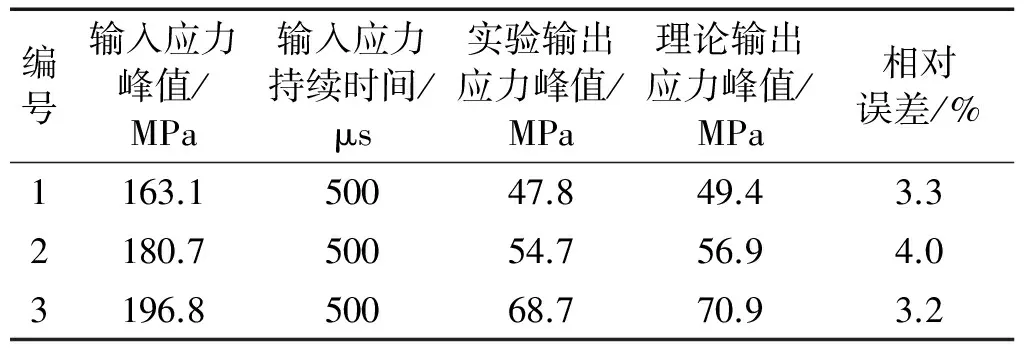
表3 不同输入应力下理论计算与实验数据对比

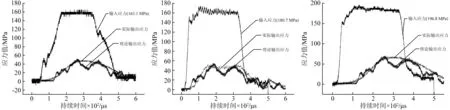
(a) (b) (c)图5 不同输入应力下理论输出应力与冲击实验输出应力曲线Fig.5 The relationship between theory output stress and test output stress curves in different input stress

通过图5和表3可知，在同样输入载荷情况下，理论计算得到作用于弹载器件的输出应力峰值与实验所测误差不到4%，说明模型计算结果和冲击实验结果一致性较好，验证了本文所建理论模型的正确性。这里特别指出，由于应力波传播后的原因，输出应力相对于输入应力存在着时延现象。

3 火炮发射环境下的过载时间累积效应分析

由于不同口径的身管火炮，采用不同发射装药时，弹丸在膛内的加速度随时间变化曲线均存在着较大不同。为研究问题的方便，可将弹丸发射时在膛内的加速度时程曲线拟合为折线，如图6所示。

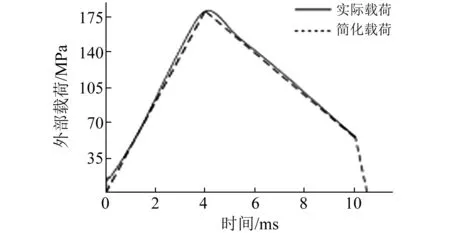
图6 火炮发射环境下弹丸在膛内的外载时程曲线Fig.6 The curve of external load in artillery launch environment

第一次到达左端面

第一次到达右端面

第二次到达左端面

(5)

以此类推，应力波经过奇数次传播后会到达减载组件的左端，经过偶数次传播后会到达减载组件的右端，故减载组件左、右两端的应力状态分别为奇、偶次应力波传播后应力的叠加，故得到减载组件左右端应力状态分别为

(6)

所以弹丸内部各截面上质点的应力状态并不相同，整个弹丸在应力波的反复传播过程中高速向前运动，此时弹载器件所受应力将会一直处在持续均匀化过程中，即产生过载的时间累积效应。

4 火炮发射环境下过载累积效应计算

经过前面分析，在SHPB实验环境下，将表2材料参数带入控制方程式(4)已经获得了和实验数据一致的结果，如表3所示。虽然火炮发射环境下控制方程组和SHPB实验一样，都是方程式(4)，但减载组件应变率在火炮发射环境下为10～100 s-1量级，远小于在SHPB实验环境下的100～1 000 s-1量级，故表2中的材料参数数值也会发生变化。注意到构成减载组件的橡胶材料是随着应变率增大，硬化效应增大的材料[11]，故火炮发射环境下材料硬化效应应该介于SHPB冲击环境和准静态环境之间，故虽然无法直接通过实验手段获得火炮发射环境下弹载器件及其减载组件的动态本构参数，但可以根据SHPB实验和准静态实验数据，将不同应变率下本构参数拟合，获得本构参数与应变率之间的关系[12]，从而得到火炮发射环境下弹载器件及其减载组件的动态本构参数，如表4所示。

表4 火炮发射环境下试件本构参数数值

将参表4中的本构参数带入方程式(4)，结合边界条件式(6)，从理论上求解弹载器件在火炮发射环境下所受应力，并且将SHPB杆冲击实验的数据作为对照，如表5所示。

从表5可以得知，在采用相同的减载组件材料和弹载器件时，取同样的输入应力峰值，火炮发射环境下计算得到作用于弹载器件的输出应力峰值，相比SHPB压杆冲击实验有明显的增大，这说明，在外载峰值相同的条件下，随着载荷作用时间延长，弹载器件承受的应力会出现明显的累积增长。

表5 冲击实验与火炮发射环境下的输入/输出应力对比

为进一步研究过载的时间累积增长规律，以文中所研究的弹载器件及其减载组件为对象，利用建立的方程式(4)，通过设定不同的输入应力峰值和输入应力持续时间，即可得到作用于弹载器件的输出应力峰值。

图7 输出应力峰值与输入应力持续时间变化关系Fig.7 The relationship between peak output stress and overload time of input stress

在作用于弹载器件上输入应力峰值一定的情况下，可以假设输出应力峰值Y与输入应力持续时间T的关系符合一次多项式，通过数值分析，可得到两者关系的近似表达式为

(7)

Y=1.133 4T+0.32σ0

(8)

式(8)即为过载时间累积效应的经验计算公式，也是方程式(4)的简化求解方法。从式(8)可以看出，对于文中所研究的弹载器件及其减载组件，在已知输入应力峰值σ0和输入应力持续时间T情况下，即可估算得到作用于弹载器件的应力峰值Y，并据此判断弹载器件在该火炮载荷环境下的可靠性。需要说明的是，式(8)中各项参系数的大小，是通过对本文所研究的弹载器件及其减载组件进行冲击试验并对试验数据进行拟合得来，对于其他类型的弹载器件及其减载组件，可根据本文所建的理论分析模型进行求解。

5 结 论

(1)针对弹载器件在不同冲击实验环境下承受的过载存在着时间累积现象问题，文章以某型特种弹所用弹载光电器件及其减载组件为例，采用应力波理论，研究了弹载器件在不同时延高过载环境下的过载累积效应和应力计算方法，实验验证了理论分析方法的正确性，为不同火炮发射环境下弹载器件的抗高过载设计提供了分析依据和方法参考。

(2)在同样过载峰值条件下，由于持续时间的不同，使作用于弹载器件上的应力也会存在着明显不同。作用于弹载器件上的应力会随着外载时间的延长出现累积增长，该应力值相比同样峰值的短时间外载要明显变大，导致弹载器件更易损坏；通过数值拟合，得到了过载时间累积效应的经验计算公式，简化了求解方法，为不同类型弹载器件及其减载组件的设计提供了方法参考。

[ 1 ] 钱立志，陶声祥.特种弹技术[M].北京：解放军出版社，2003：17-18.

[ 2 ] 胡时胜，王礼立，宋力，等. Hopkinson压杆技术在中国的发展回顾[J]. 爆炸与冲击， 2014, 34(6): 642-648.

HU Shisheng, WANG Lili, SONG Li, et al. Hopkinson bar technique development review in China[J]. Explosion and Shock Waves, 2014, 34(6): 642-648.

[ 3 ] 梁增友， 高位， 陈智刚. 泡沫金属/金属管塑性变形缓冲器降低弹载设备过载的数值模拟[J]. 兵工学报， 2013， 34(8): 1041-1045.

LIANG Zengyou， GAO Wei， CHEN Zhigang. The numerical simulation of metal foam /metal tube plastic deformation energy absorber for reduction in overload of projectile-borne equipment[J]. Acta Armamentarii, 2013, 34(8): 1041-1045.

[ 4 ] 王鹏飞，徐松林，李志斌，等．高温下轻质泡沫铝动态力学性能实验[J]．爆炸与冲击， 2014, 34(4): 433-438.

WANG Pengfei, XU Songlin, LI Zhibin, et al. An experimental study on dynamic mechanical property of ultralight aluminum foam under high temperatures[J]. Explosion and Shock Waves, 2014, 34(4): 433-438.

[ 5 ] 李俊. 弹载器件抗高过载机理研究[D]. 合肥： 陆军军官学院， 2011： 107-108.

[ 6 ] 宁全利， 蒋滨安， 梁希， 等．火炮发射环境下弹载光电器件结构动态响应研究[J]．兵工学报， 2015， 36(11)： 2185-2189．

NING Quanli, JIANG Bin’an, LIANG Xi, et al. The structural dynamic response of projectile-borne optoelectronic devices during launching[J]. Acta Armamentarii, 2015, 36(11): 2185-2189.

[ 7 ] 宁全利．高过载环境下弹载器件结构动态响应研究[D]．合肥： 陆军军官学院， 2014.

[ 8 ] 王礼立， 施绍裘， 陈江瑛, 等．ZWT非线性热黏弹性本构关系的研究与应用[J]．宁波大学学报(理工版)， 2000， 13(增刊1)： 141-149．

WANG Lili, SHI Shaoqiu, CHEN Jiangying, et al. The research and application of constitutive relation of nonlinear not ZWT[J]. Journal of Ningbo University (Nature Science & Engineering), 2000, 13(Sup 1): 141-149.

[ 9 ] 王礼立， 王永刚．应力波在用SHPB研究材料动态本构特性中的重要作用[J]．爆炸与冲击， 2005， 25(1)： 17-25．

WANG Lili, WANG Yonggang. The important role of stress wave in the study of dynamic constitutive properties of materials by SHPB[J]. Explosion and Shock, 2005, 25(1): 17-25.

[10] 钱立志， 宁全利， 李俊， 等．基于分离式霍普金森压杆的弹载器件动态特性模拟研究[J]．兵工学报， 2015， 36(10)： 1875-1881．

QIAN Lizhi, NING Quanli, LI Jun, et al. Dynamic characteristics simulation of projectile-borne device based on split Hopkinsion pressure bar[J]. Acta Armamentarii, 2015, 36(10): 1875-1881.

[11] 庞宝君， 杨震琦， 王立闻， 等. 橡胶材料的动态压缩性能及其应变率相关的本构模型[J]. 高压物理学报， 2011, 25(5): 407-415.

PANG Baojun, YANG Zhenqi, WANG Liwen, et al. Dynamic compression properties and constitutive model with strain rate effect of rubber material[J]. Chinese Journal of High Pressure Physics, 2011, 25(5): 407-415.

[12] 周相荣, 王强, 王保珍. 一种基于Yeoh 函数的非线性黏超弹性本构模型及其在冲击仿真中的应用[ J] . 振动与冲击, 2007, 26(5): 33-37.

ZHOU Xiangrong, WANG Qiang, WANG Baozhen. A based on Yeoh function nonlinear viscous elastic constitutive model in impact simulation application[J]. Journal of Vibration and Shock, 2007, 26(5): 33-37.