基于双势阱系统的混沌振动研究

刘树勇， 位秀雷， 王 基， 俞 翔

(海军工程大学 动力工程学院，武汉 430033)

混沌振动是混沌科学研究的重要课题，国内外学者围绕混沌振动的应用、控制和识别等问题开展了广泛的研究[1]。为了应用有益混沌振动，Yu等[2-3]提出广义混沌同步技术消减了船舶辐射噪声线谱，提高了其隐身性能；龙运佳等[4]研究了混沌振动压路机的应用，提高了压实效果。为了控制有害的混沌振动，韩建群等[5]应用滑模控制方法隔离了设备中的Lorenz混沌振动，消除了破坏仪器设备混沌运动；高远等[6]应用自适应跟踪控制方法，抑制了汽车悬架的大幅值混沌振动，有效降低了悬架垂向振动加速度；熊怀等[7]研究了非线性能量阱(Nonlinear Energy Sink, NES)对振动的抑制方法，得到了阻尼对NES的影响规律。目前，在混沌振动的研究方法上，数值仿真研究和试验研究仍然是两种主要手段[8]。陈立群等[9]通过仿真研究了混沌振动的开闭环控制技术；韩保红等[10-11]应用数值方法研究了混沌振动的主动隔振问题；梁山等[12]对两自由度汽车悬架模型的非线性混沌振动进行了仿真与实验研究，揭示了该系统存在混沌的可能性。

事实上，由于混沌振动问题的复杂性[13]，导致混沌试验研究具有一定的困难，目前大部分研究工作还局限在理论分析和计算层面，缺乏试验的验证，特别是要产生稳定的、可重复出现的混沌是一件非常困难的工作。然而，要将混沌应用于工程实际，必须开展深入的试验研究，掌握混沌产生的实际条件、混沌出现的规律以及不同参数对混沌的影响，在这方面，国内外学者都进行了尝试。任成龙等[14]为了模拟路面的复杂激励，应用多连杆机构设计了悬架振动台，取得了较好的实验结果。Moon[15]开展了悬臂梁的混沌振动试验研究，主要探讨了两种情况下系统的响应：一是梁的振动幅值处于较小的范围内，可以简化为线性方程，但其自由端受非线性力或边界条件有非线性特性；二是梁振动幅值非常大，本身有明显的几何非线性。在这些条件下，系统可能产生混沌振动。虽然这些研究工作为混沌试验提供了思路，但具体还存在如下问题需要解决：①如何在系统中产生持续稳定的混沌运动；②如何准确确定实际系统的混沌参数区域；③如何对复杂条件下的混沌信号进行有效分析；④如何在工程实际中实现小振幅的混沌运动。本文利用Moon提出的双势阱系统设计了单端磁吸式混沌振动试验装置，并开展了深入的理论和试验研究，通过对实测数据进行分析，结果表明，该装置切实可以产生稳定的、可重复实现的混沌振动，从而为后续混沌应用研究奠定了坚实的基础。

1 双势阱系统的非线性特征

由磁铁和悬臂梁构成的双势阱系统动力学方程可以简化为

(1)

式中：ξ为系统无量纲阻尼参数；γ为无量纲线性刚度；β为无量纲非线性刚度；f无量纲激励力幅值。对于式(1)，其弹簧作用力为：F(z)=-γz-βz3定义其势函数V(z)为V(z)=γz2/2+βz4/4。当参数的取值为γ=-1，β=1时，双势阱如图1所示。

因此，质点可以在双势阱M和N之间以及在单势阱M或N内运动。运动形式一般分为以下几种情况：质点在双势阱M和N之间周期振荡，物理系统呈现大幅值的周期振动，如图1(a)所示；质点在单势阱M和N内运动，物理系统呈现出小幅值的周期振动，如图1(b)和图1(c)所示；质点在双势阱M和N之间无规律来回振荡，具体表现为在单边势阱M和N内运动后，越过势阱壁垒进入到另一个势阱中，但在势阱中运动时间不同，是非周期振动模式，如图1(d)所示。但由于它是在确定性系统中产生的类随机行为，因而具有混沌性质。

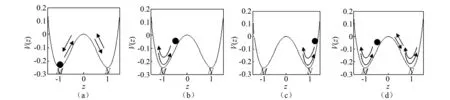
图1 双势阱示意图Fig.1 Two potential well sketch map

(2)

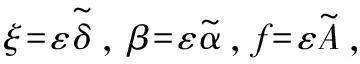
(3)

(4)

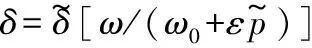
假设系统的响应中包含了快变和慢变分量，具有多时间尺度特征，分别设为T0=t，T1=εt，因此式(4)可以写为

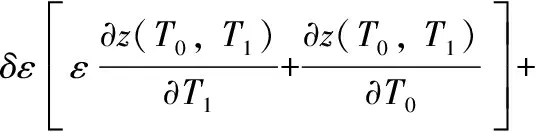
(5)

式(5)的解可以展开成

z(T0,T1)≈z0(T0,T1)+εz1(T0,T1)

(6)

将式(6)代入式(5)得到

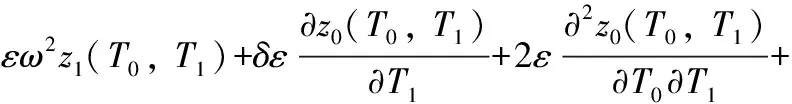
(7)

令等式两边小参量ε的系数为零得到

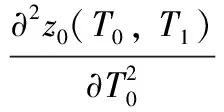
(8a)

pz0(T0,T1)+αz0(T0,T1)3+ω2z1(T0,T1)+

(8b)

令基本解幅值和相位为时变参数

z0(T0,T1)=B(T1)cos(T0+φ(T1))

(9)

联立式8(b) 和式(9)得到

(10)

将式(10)等式右边项应用三角函数关系展开，并消除共振项，即令cos(T0+φ(T1))和sin(T0+φ(T1))的系数等于零得到

δB(T1)+2B′(T1)=0

(11a)

(11b)

因此可以求出

(12a)

(12b)

(13)

式中，φ0为积分常数。联立式(10)和式12(a)得到

(14)

因此，可以由式(14)解出z1(T0,T1)为

z1(T0,T1)=-αB(T1)3cos(3T0+φ(T1))/4(ω2-9)

(15)

因此求得系统的解为

(16)

以T0=t，T1=εt替换后得到

(17)

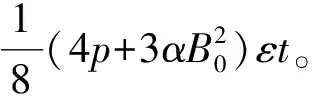
应用平均法[18]推导了式(5)的幅值和频率之间的关系

16γ2[p2ε2+δ2ε2+2pε(ω-1)2+(ω-1)4]}=0

(18)

式中，参数γ为平均法计算过程中所采用的极坐标幅值，其本质含义为Van der Pol平面上振动幅值的大小。当ε=1,α=1,ω=1,A=6,δ=0.5,δ=1.0,δ=1.5时，改变调节因子p的大小，得到p-γ曲线如图2所示。从图中可以观察到系统的非线性“舌状”结构特征。

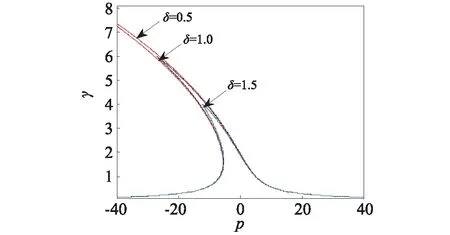
图2 系统的幅值特征曲线Fig.2 Amplitude frequency characteristic curve

2 试验台架结构设计

为了验证系统的非线性以及可能具有的混沌特征，开展了试验研究。根据混沌产生的必要条件，在混沌振动试验装置设计过程中，需要选择合适的非线性元件作为试验台的组成部分，主要利用系统结构非线性、材料非线性或者电路的非线性等产生混沌；其次确保系统中没有随机信号输入，从而实现由确定性系统产生类似随机的不确定性行为；在此基础上，编制混沌识别程序对系统的动力学行为进行识别，通过定性分析技术对采集的时间历程图进行目视观察，同时利用相空间重构原理，观察实测时间序列相平面图、Poincaré截面图；利用定量分析方法提取信号的特征，进行Fourier分析得到信号的频谱特征；计算信号的分形维数和Lyapunov指数；调节系统参数，观察到系统由不同周期态进入混沌态的途径。

基于以上考虑，双势阱单端磁吸式混沌振动装置如图3所示。装置由如下部分组成：激振器、支座、薄弹片、磁铁、小铁片、外部固定框架、固定弹片装置。各部件的具体功能为：①激振器，提供稳定外部激励，保持整个系统持续稳定振动；②支座，固定激振器，为了保证装置在水平方向上不受其他外力影响，需严格保持激振器水平放置；③薄弹性片，为整个装置的主体元件，为保证薄片具有良好的恢复力，刚度不易太硬，并且薄片的宽度不宜太小，这样可以减少薄片做水平摆动之外的运动；④磁铁(方形磁铁)， 提供弹片端部吸引力，固定磁铁的支座可以左右水平移动，进而调节磁力作用距离；⑤质量块，安装在薄弹片自由端，受到磁力作用，它和磁铁一起形成了装置的双势阱，为保证薄弹片不产生水平摆动之外的运动，其质量不宜过大；⑥外部固定框架，框架需满足两个要求，不能是磁性材料，以免对弹片运动形成外部干扰；质量不宜过大，否则难以保持整个框架的水平性，从而弹片的水平摆动会受到外部力的干扰；⑦弹片固定装置，在两个夹紧螺母和弹片之间设置一个方形铁片，将螺母和弹性片之间的点接触扩展成面接触，从而使弹片固定更牢靠；⑧设计实验参数，激光位移传感器，型号CD33-30NV，测试最大位移为±4 mm，最大允许误差为±0.1%F.S.；激光位移传感器与梁的距离为30 mm；梁的长与宽尺寸为155 mm×20 mm；磁铁尺寸长宽高为11 mm×6 mm×9 mm；磁铁顶端到底面高度为24 mm；质量块重量为5 g。

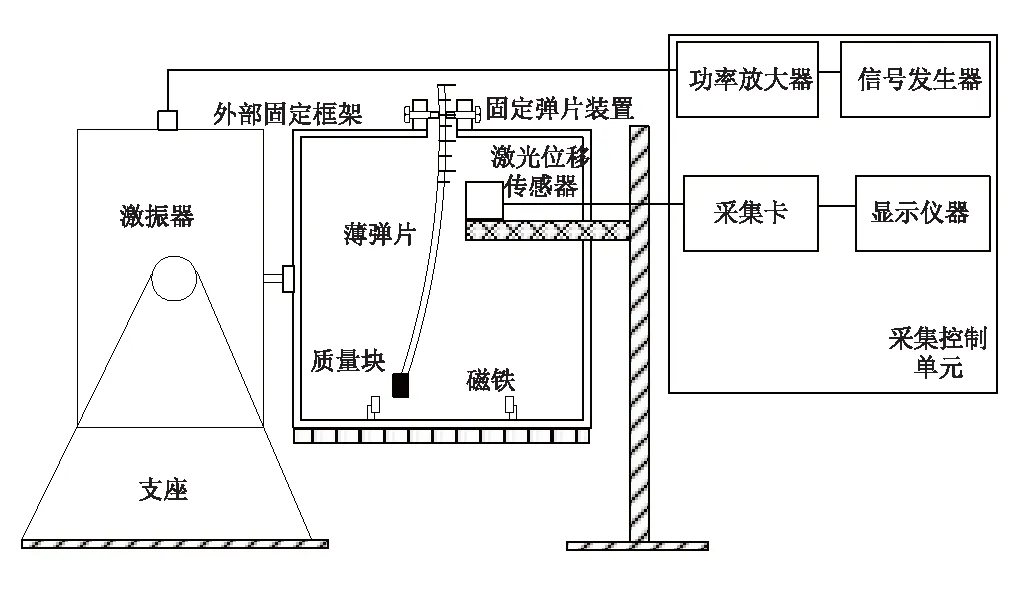
图3 双势阱单端磁吸式混沌振动装置Fig.3 Sketch of the experimental rig

3 试验步骤

实验本质为正弦信号的慢速频率扫描实验，扫描频率范围为5～25 Hz，采样频率为2 kHz，数据采集时长为5 s。具体实验步骤为：

步骤1 安装实验装置，设置磁铁距中心线的距离、无激励时薄弹片距底端的距离，布置位移传感器；

步骤2 将功率放大器置于高阻位置，设置最大电流限制值，并通过调节增益来实现激励力大小的改变；

步骤3 打开数据采集系统以及信号发生系统，打开LabVIEW软件，建立采集信号的时间历程窗口、功率谱窗口及相图以作实时观察；

步骤4 固定激励频率于特定值，调节功率放大器增益旋钮，观察信号的时间历程图与功率谱图，待其稳定后采集数据以备后处理之用，数据文件按H××L××S×××.lvm命名，H后为激励幅值，L后为磁铁距中心线的距离值，S后为无激励时薄弹片距底端的距离值，在文件名中以p标识小数点；

步骤5 以步长为0.1 Hz增加频率，重复步骤4，直至完成一定范围的频率扫描；

步骤6 改变磁铁距中心线的距离、无激励时薄弹片距底端的距离，重复步骤3～步骤5；

步骤7 信号分析流程，对信号时域图进行目视观察、提取和分析实测数据的频率特征、计算相空间重构参数、重构原系统的吸引子、计算吸引子的特征指数；

步骤8 根据分析结果，给出系统的可能的混沌参数区域；

步骤9 提出改进试验方案和进一步研究内容。

4 试验结果

4.1 系统响应随激振系统增益变化的结果

根据扫频调试，发现当激励频率大于10 Hz时，系统的响应呈现丰富的动力学特征，因此，本试验中将重点研究的频率范围设置在10 ～25 Hz。同时，考虑到功率放大器的增益过大时，将对试验装置产生破坏性作用，因此增益的范围确定为0～1.5 V。

当激励频率为15.6 Hz，激振系统功率放大器的增益为0.1时，系统在右势阱中处于周期1状态，时间历程曲线如图4所示，振动的最大幅值为0.056 mm，从频谱图中可以观察到系统出现了基频和三倍频46.8 Hz，系统的重构吸引子为一个极限环，从而证实了近似解析解分析的正确性。在这种状态下，用力杠加入小的外部扰动，系统在两个磁铁之间振荡，随后落入左势阱并进入周期1运行状态，这表明外部激励力不足以使其越过势阱壁垒，因而被限制在单边势阱内。

当激励频率为15.6 Hz，激振系统的增益为0.5时，系统的振动幅值增大，达到0.172 1 mm，但仍然处于周期1运动状态，如图5所示。从时域图和频域图中，可以观察到系统的规则运动以及明显的线谱特征。重构了系统的吸引子，它是一个极限环。应用改进的Poincaré截面法对系统的响应进行了分析，得到了截面图。注意实测数据Poincaré截面图和传统的仿真数据不同，它是一个点簇而不是单个点，因此在编程过程中，需要将距离近的截点归属到同一点，这样才能反映系统的本质特性，这和仿真研究有明显的差异，如图5(d)所示。

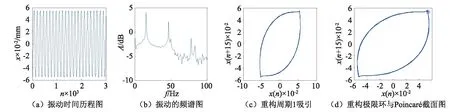
图4 激振系统增益为0.1 V时系统的振动响应Fig.4 The vibration response when the excitation gain is 0.1 V

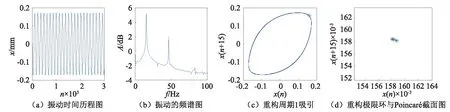
图5 激振系统增益为0.5 V时系统的振动响应Fig.5 The vibration response when the excitation gain is 0.5 V

继续增大增益为0.8时，系统的振动幅值进一步增加，但此时的状态是一种临界状态。用力杠加入小的扰动后，系统进入混沌状态。系统在左右势阱之间以混沌模式振荡。有趣的是，系统随后又落入左单边势阱并处于周期1振动，这是一种不稳定混沌现象。而增益参数为0.95时，系统出现1/2次谐波，频率为7.83 Hz，表明此时系统出现了倍周期分岔行为，如图6所示。

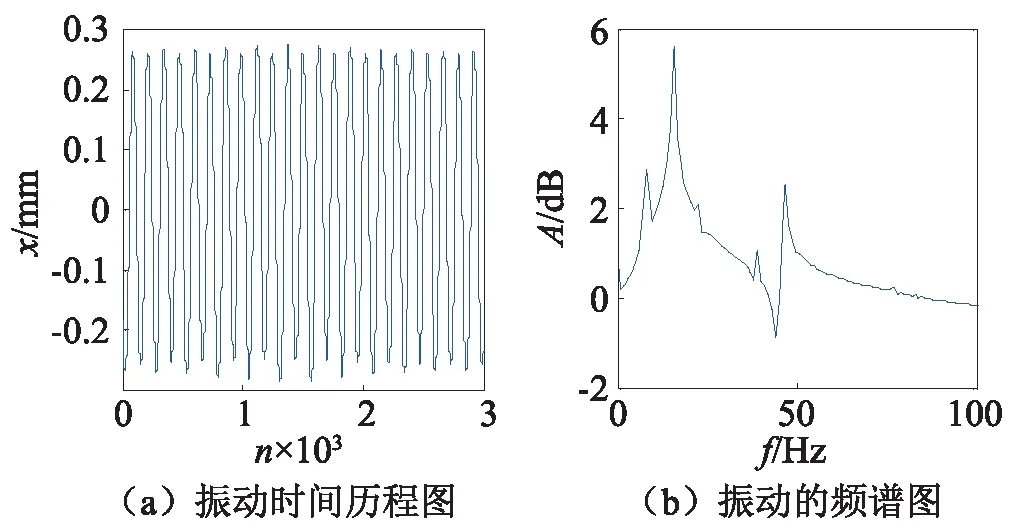
图6 激振系统增益为0.8 V时系统的振动响应Fig.6 The vibration response when the excitation gain is 0.8 V

在增益为0.98时，无需力杠扰动，系统自动进入稳定的混沌运动状态。时间历程图如图7(a)所示，具有明显的貌似随机特征，功率谱呈现宽谱。重构相空间参数中嵌入维数为4，延迟时间为16。得到的重构混沌吸引子如图7(e)所示，计算得到的最大LE为0.031 3，关联维数为2.129。

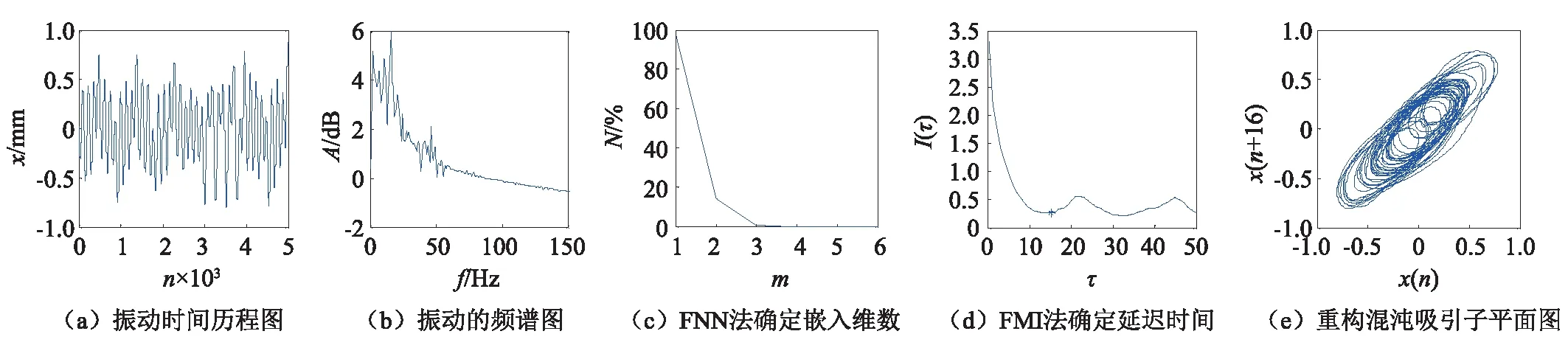
图7 激振系统增益为0.98 V时系统的振动响应Fig.7 The vibration response when the excitation gain is 0.98 V

4.2 系统响应随激振频率变化的结果

由前面的试验可总结出两个规律：①激振系统的增益为0.5时，不容易进入混沌状态，而是在单边势阱内处于周期1运动；②激振系统增益大于0.95时，系统的动力学行为非常丰富，可以产生包括混沌在内的不同振动模式。为了证实该结论，在增益为0.5的条件下，改变激励频率从10～20 Hz，系统的响应都为周期1模式。结果发现，在频率为15～17 Hz，加入小的外部扰动，系统能产生暂态混沌行为，随后落入势阱内，处于周期1状态。

为了观察系统的混沌响应并进一步证实以上规律的准确性，将激振系统的增益固定为1，由小到大增加系统的激励频率。当频率为5～10 Hz时，系统处于周期1状态；当激励频率大于10 Hz时，系统的响应特征非常丰富：在10～16 Hz时，产生混沌振动；在16.6 Hz时，系统出现周期2行为，如图8所示，计算其LE为-0.008 5。在17～19 Hz时，又产生并保持稳定的混沌运动，如图9所示。而在高频时，系统出现了逆分岔行为，由混沌自动进入周期运动，19 Hz时，产生周期3运动，如图10所示；在19.4 Hz时，产生单势阱内的多周期运动，如图11所示。此外，还观察到了一些有趣的现象，在23 Hz时，质量块穿越势阱壁垒在两个势阱之间来回运动，产生了大幅值的多周期振动；在30 Hz激励时，装置出现轰鸣声，系统可能出现了共振现象。越过共振频率后，振子在单边势阱内呈周期1运动模式。

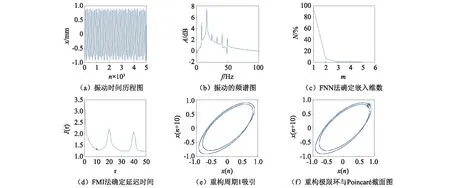
图8 系统产生的周期2振动Fig.8 Periodic 2 motion of the system

图9 系统产生的混沌振动Fig.9 Chaotic motion of the system

图10 激励频率为19 Hz系统产生的周期3振动Fig.10 Periodic 3 motion of the system

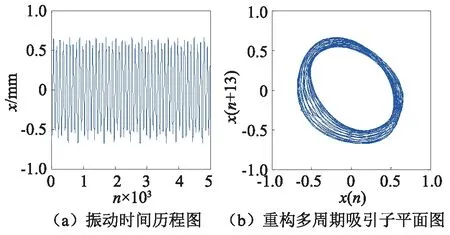
图11 激励频率为19.4 Hz时系统产生的多周期振动Fig.11 Multi periodic motion of the system

5 结 论

应用多尺度法可以有效求出双势阱系统自由振动响应的近似解析解，从响应表达式中可知系统动力学行为中存在慢变分量和快变分量，并存在超谐波响应。采用平均法得到了系统的幅频关系表达式，给出了振动幅值和频率调节因子之间的舌状结构曲线，揭示了系统的非线性本质特征。成功设计并加工了双势阱理论的机械式混沌振动试验装置，其意义在于进一步证实了机械系统中不仅能够产生可以复现的、稳定的混沌振动，而且可以通过试验获得混沌参数区域，为混沌的工程应用研究提供了可靠的试验手段。

通过实测数据的分析，观察到了试验中的次谐波现象，它的出现的预示着混沌产生；观察到了超谐波现象和混沌现象，同时观察到了一些有趣的新现象：如系统周期1运动存在两种模式，一种是在两个势阱之间周期振荡，另一种是陷入某一个势阱内做周期1运动，试验研究证实了理论分析的有效性。后续研究中，还需要完成一些工作：如弹片的长度变化与刚度变化对混沌的影响、附加质量的改变、多频激励、多自由度等因素对系统的影响、多势阱系统的三维混沌振动、设计能够精确控制初始条件的结构以及验证本项目组编制的混沌在线识别系统。

致谢：

杨庆超讲师和Southampton University Solent Institution of Acoustic: Jian Jiang, Chris, Lee, Lawrance的讨论。

[ 1 ] ZAMBRANO S，SABUCO J， SANJUAN M A F. How to minimize the control frequency to sustain transient chaos using partial control[J]. Communications in Nonlinear Science and Numerical Simulation，2014，19(3)： 726-737.

[ 2 ] YU Xiang， ZHU Shijian， LIU Shuyong. A new method for line spectra reduction similar to generalized synchronization of chaos[J]. Journal of Sound and Vibration，2007， 306(3/4/5)：835-848.

[ 3 ] 俞翔, 朱石坚, 楼京俊. 基于碰撞振动的隔振系统混沌化实验研究[J]. 振动与冲击, 2014, 33(18): 59-64.

YU Xiang, ZHU Shijian, LOU Jingjun. Tests for chaotification method of a vibration isolation system with a vibro-impact subsystem [J].Journal of Vibration and Shock, 2014, 33(18): 59-64.

[ 4 ] 龙运佳，杨勇，王聪玲. 基于混沌振动力学的压路机工程[J]. 中国工程科学，2000，2(9)： 76-79.

LONG Yunjia， YANG Yong， WANG Congling. Road roller engineering based on chaotic vibration mechanics[J]. Engineering Science， 2000， 2(9)： 76-79.

[ 5 ] 韩建群，郑萍.一种简单的Lorenz混沌振动主动隔振方法[J].系统工程与电子技术，2006，128(10)： 1566-1568.

HAN Jianqun，ZHENG Ping. Active control isolation for the Lorenz chaotic vibration with a simple method[J]. Systems Engineering and Electronics， 2006， 128(10)： 1566-1568.

[ 6 ] 高远，耿兆云，范健文. 汽车悬架系统中混沌振动的自适应跟踪控制研究[J]. 机械设计与制造, 2013(12)： 198-201.

GAO Yuan，GENG Zhaoyun，FAN Jianwen. Control chaos in automobile suspension system via adaptive tracking control method[J]. Machinery Design & Manufacture， 2013(12)： 198-201.

[ 7 ] 熊怀,孔宪仁,刘源.阻尼对耦合非线性能量阱系统影响研究[J]. 振动与冲击, 2015, 34(11): 116-121.

XIONG Huai, KONG Xianren, LIU Yuan. Influence of structural damping on a system with nonlinear energy sinks[J]. Journal of Vibration and Shock, 2015, 34(11): 116-121.

[ 8 ] WIERCIGROCH M， SIN V W T, LI K. Measurement of chaotic vibration in a symmetrically piecewise linear oscillator[J]. Chaos Solitons & Fractals， 1998， 9(1)： 209-220.

[ 9 ] 陈立群，刘延柱. 混沌振动系统的开闭环控制[J]. 应用科学学报，1999， 17(4)： 445-449.

CHEN Liqun， LIU Yanzhu. The open-plus-closed-loop control for chaotic oscillations[J]. Journal of Applied Sciences， 1999， 17(4)： 445-449.

[10] 韩保红，马英忱，闫石. 用Matlab仿真非线性混沌振动的主动隔振研究[J]. 控制与决策， 2003， 18(1)： 120-122.

HAN Baohong，MA Yingchen，YAN Shi. Active control isolation research for a class of nonlinear chaotic vibration systems[J]. Control and Decision， 2003， 18(1)： 120-122.

[11] 韩保红，闫石，焦耀斌，等.一类非线性混沌振动的主动隔振实验研究[J]. 噪声与振动控制，2002， 22(2)： 24-28.

HAN Baohong，YAN Shi，JIAO Yaobin，et al. Active control isolation research for a class of nonlinear chaotic vibration systems[J]. Noise and Vibration Control， 2002， 22(2)：24-28.

[12] 梁山，郑剑，朱勤，等. 非线性车辆模型混沌振动的仿真与实验研究[J]. 机械强度，2012， 34(1)： 6-12.

LIANG Shan，ZHENG Jian，ZHU Qin，et al. Numerical and experimental investigations on chaotic vibration of a nonlinear vehicle model over road excitation[J]. Journal of Mechanical Strength， 2012， 34(1)： 6-12.

[13] YOSHIDA K，SATO K, YAMAMOTO S，et al. Charac-terization of chaotic vibration without system equations[J]. International Journal of Non-linear Mechanics， 1997， 32(3)： 547-562.

[14] 任成龙，葛翔. 悬架混沌振动台的设计[J].南京工程学院学报(自然科学版)， 2009， 7(4)： 37-42.

REN Chenglong，GE Xiang. Design of suspension chaotic vibration table[J]. Journal of Nanjing Institute of Technology(Natural Science)， 2009， 7(4)： 37-42.

[15] MOON F C. Chaotic vibrations： an introduction for applied scientists and engineers[M]. New York： Wiley， 1987.

[16] YAN Yan, WANG Wenquan, ZHANG Lixiang. Applied multiscale method to analysis of nonlinear vibration for double-walled carbon nanotubes[J]. Applied Mathematical Modelling, 2011, 35(5): 2279-2289.

[17] MITCHELL L, GOTTWALD G A. On finite-size Lyapunov exponents in multiscale systems[J]. Chaos, 2012, 22(2): 1-26.

[18] OKABE T, KONDOU T, OHNISHI J. Elliptic averaging methods using the sum of Jacobian elliptic delta and zeta functions as the generating solution[J]. International Journal of Non-Linear Mechanics, 2011, 46(1): 159-169.