矩阵输入的多层前向神经网络学习算法

黄旭进,曹飞龙

(中国计量大学 理学院,浙江 杭州 310018)

随着现代科学技术的不断发展,现代社会的各个领域都得到了快速发展,尤其是以计算机和信息技术为代表的人工智能应用领域更是这样.在这些领域中,人工神经网络是最具有代表性的,它的发展给人类社会带来了巨大的进步.人工神经网络是一种旨在模拟人脑结构及其功能的智能信息处理系统(被简称为神经网络),其主要有两大功能: 一是通过存储信息和学习规则进行自适应训练的记忆功能；二是通过对大量样本对学习后提取蕴含在其中的函数映射功能.早期的神经网络具有简单的学习能力,一般只用于线性分类，如感知器(Perceptron)[1].随后经过许多科学家的努力和深入研究,神经网络由单层拓展到多层，特别是BP算法[2 -3](Back Propagation Algorithm)的诞生,给神经网络的发展注入了新能量,使得BP神经网络成为最广泛的应用[4-6].

神经网络已普遍应用于信息处理、自动化、工程、医学、经济等诸多领域，其中信息处理中的图像分类[7-8]是神经网络的重要研究内容.图像分类主要分为两大步骤：图像的特征提取和分类.图像的特征提取有很多种方法,如主成分分析法[9-10](PCA)、线性判别分析法[11-12](LDA)、前向神经网络提取法[13-14](FNN)、多尺度法[15-17](MDA).因为神经网络具有良好的特征学习能力,可以根据确定的学习规则分析出样本和输出的内在联系,故其相对于上述另外三种方法在特征提取上具有很好的优势.分类是在图像提取特征的基础上进行的,根据提取的特征信息来确定它的类属性.一般来说,特征提取原图像信息越完整,分类效果就越好.

在传统的神经网络里,其输入均是向量形式.特别是在利用神经网络作为分类器时,一般是把图像拉成列向量,这势必破坏了图像空间的原有信息.这一简单的处理肯定会给分类效果带来一定的影响，为了克服以上缺点,Dai等人在文献[18]提出了一种方法，即是通过左右投影向量将图像的二维空间信息投影到一维上.这一过程的转换避免了破坏图像的空间结构,将矩阵图像直接作为神经网络的输入.又因为它是单隐层的,故称之为单隐层矩阵输入的神经网络.通过与向量形式输入的单隐层神经网络的实验对比,单隐层矩阵输入的神经网络取得了很好的效果.但是由于单隐层矩阵输入神经网络的客观局限性,它不能足够好地表达样本特征信息.基于多层神经网络具有更好的特征提取能力和泛化能力,本文在文献[18]的基础上提出了多层矩阵输入的神经网络算法,并将此算法应用于图像分类中.通过实验对比,本文算法取得了良好的效果.

本文章节结构如下：第一节介绍向量输入和矩阵输入的单隐层神经网络.第二节提出多隐层矩阵输入的神经网络反向传播算法.第三节通过与向量输入和单隐层矩阵输入神经网络的实验对比,说明本文算法的优越性；通过固定隐层节点数和固定隐层矩阵的大小探究本文算法的内在关系.第四节给出本文结论.

1 单隐层前馈神经网络

在本节中,我们分别介绍向量形式输入和矩阵输入的单隐层前馈神经网络.

单隐层前向神经网络的一般形式为

(1)

式(1)中x∈Rn是输入向量,uj和bj分别是隐层的权重和偏置，βj和α是输出层的权重和偏置，L是隐层的节点数，σ是激活函数.当uj与bj满足某种随机分布，外权βj和通过最小二乘来确定时，则我们称该网络为随机权网络[19-20].在文献[21]中Igelnik和Pao已经证明随机权网络的收敛性.当uj,bj,βj和α用经典的BP算法训练获得时，我们把式(1)称为前向BP神经网络(FNN).

传统上，神经网络的输入是向量形式.如果将该网络模型应用于图像处理，如图像分类问题,我们必须要对样本图像进行预处理,即把图像拉成列向量作为网络的输入.这一简单的处理势必破坏像素与像素之间的关联性,破坏了图像的空间特征信息,势必会影响图像的分类效果.为了避免破坏图像的空间结构,文献[18]引进了单隐层矩阵输入的神经网络，分别利用左投影向量uj和右投影向量vj把矩阵投影到一维上.因为左右投影向量是经过BP算法反向更新学习的,所以保证了二维空间信息转换到一维的合理性.该网络的模型如下：

(2)

式(2)中X∈RM×N是输入矩阵；uj=[uj1,…,ujm,…,ujM]T，vj=[v1j,…,vnj,…,vNj]T和bj分别是隐层的左右投影向量和偏置；M和N分别为输入矩阵X的行数和列数；βj=[β1j,…,βoj,…,βOj]T和α=[α1,…,αo,…,αO]T为输出层的权重和偏置；L和O为隐层的节点数和输出层的节点数.

2 多隐层矩阵输入算法的提出

单隐层矩阵输入的神经网络从一定程度上解决了保持图像空间结构的问题.但是由于其客观局限性,对于具有复杂信息的样本,单隐层神经网络不能很好地学习到它的特征信息.根据深度学习的思想，多层神经网络具有更好的特征提取和泛化能力,为此我们把单隐层矩阵输入的神经网络拓展到多层矩阵输入的神经网络.即对于输入样本X,多层矩阵输入的神经网络的映射f:RM×N→RK.

(5)

记

(4)

(5)

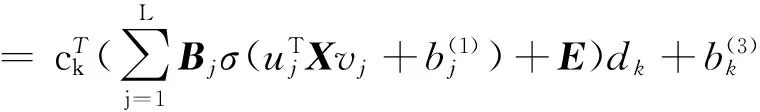
(6)

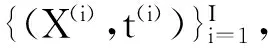
(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

Δw(i)=γΔw(i-1)-(1-γ)η▽w,

(16)

w(i)=w(i-1)+Δw(i).

(17)

3 实 验

3.1 实验环境与数据库

本文的所有实验都是在32 GB内存和CPU E5-1620 @3.5 GHZ的WIN10系统下完成的,实验工具是Matlab2015b.为了避免随机性,本文每个实验重复5遍，并取其平均值.

为了验证本文提出的算法的图像分类能力,我们将对ORL、UMist、Yale和FERET人脸数据库进行分类实验,如图1，这些人脸数据库广泛被用于图像分类中

•ORL人脸数据库诞生于英国剑桥大学Olivetti实验室.该数据库采集了40个不同年龄、不同性别和不同种族对象的图像.每个对象有10张的图像,其中图像含有表情变化和光照变化等信息.可在http://www.cad.zju.edu.cn/home/dengcai下载.

•UMist人脸数据库由20人共575张图像组成.每个人具有不同角度、不同姿态的多幅图像.其中不同角度的图像主要是指从侧面到正面连续拍摄的图像.图像大小为112×92,可在此链接http://www.cs.nyu.edu/～roweis/data.htm下载.

•Yale人脸数据库由15位人员各自11张的灰度图像组成,每位人员的图像包含快乐、正常、悲伤、瞌睡、眨眼、惊讶等表情.

•FERET人脸数据库是由美国国防部CTTP建立,目的是促进人脸识别算法的研究和实用化.它包括了1 564人共14 126张图像,每人的图像均是在不同表情、光照和姿态采集的.资源共享在https://www.nist.gov/programs-projects/face-recognition-technology-feret网站.

在ORL数据库中,我们随机选取280张作为训练样本,剩下的120张作为测试样本.UMist数据库,随机选取65%作为训练样本,35%作为测试样本.在Yale数据库中,每个人训练样本与测试样本的比值7∶4.因为FERET数据库中的类数较多,我们随机抽取50人的图像进行实验,每人的训练样本与测试样本的比值为5∶2.在实验中,所有图像都归一化到[0,1]之间.

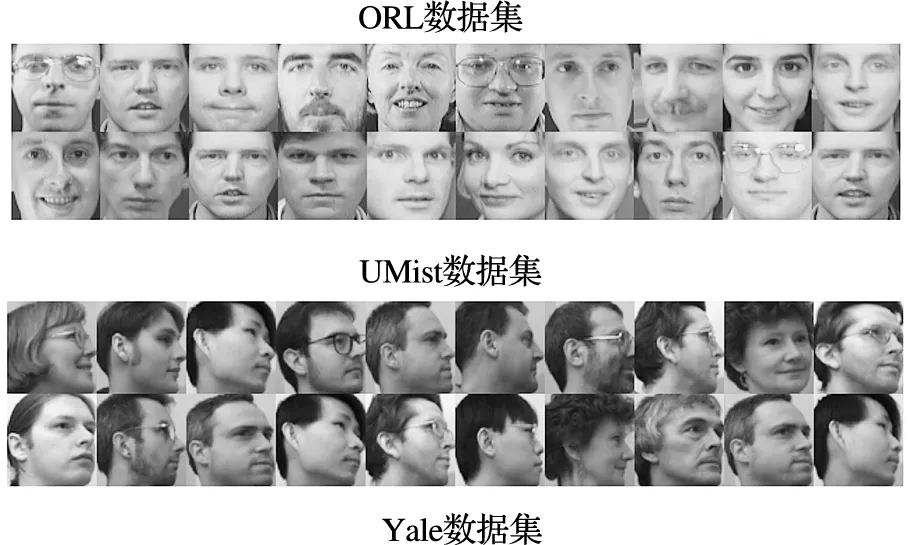
图1 不同数据库的样本Figure 1 Samples of Different Databases

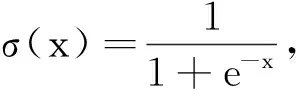
第一步： 产生网络模型并权值初始化,输入γ、η、Iters、L和bsize.

第二步： 1)根据公式(3)计算每一训练样本的输出；2)用公式(8)～(15)计算梯度▽w,根据公式(16)～(17)更新w；重复第二步

第三步： 迭代停止,确定网络.

第四步： 输入样本测试.

3.2 实验

为了验证本文提出的算法具有更好的分类能力,我们对四个数据库分别作了三个不同的实验.

实验3.2.1 本文算法与单隐层矩阵输入的神经网络(Dai)和以向量形式输入的单隐层神经网络(vecInput)算法的对比，见图2.

图2 不同数据库中三种模型算法的测试精度比较Figure 2 Comparison of testing accuracy of 3 model algorithms in different databases

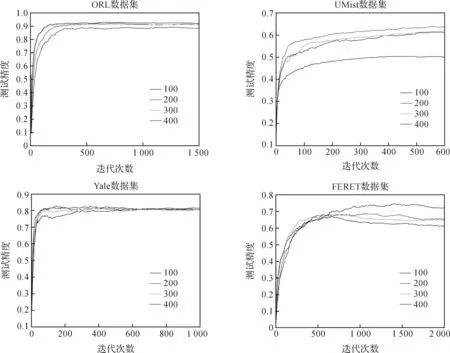
图3 第一隐层不同节点数的测试精度对比Figure 3 Testing comparison of different nodes in the first hidden layer

从图2可以看出,在不同的数据库中,本文的测试精度比单隐层矩阵输入的神经网络和单隐层向量输入的神经网络算法都要高,具体也可以看表1. 单隐层矩阵输入的神经网络采用左右投影向量把二维信息转换到一维上,没有破坏图像矩阵的空间信息.故其分类能力明显比向量形式输入的单隐层神经网络好.而本文提出的算法比单隐层矩阵输入的神经网络要好,说明本文提出的算法具有更好的特征提取能力.在UMist数据中,本文算法的分类效果相对于Dai[18]的网络只是超了少许.原因是其数据库中的图像特征信息较少.而对于具有多种表情和姿态信息的FERET数据库,本文算法的分类效果更明显.说明对于具有复杂特征的样本,多层矩阵输入的神经网络具有更好的分类能力.

实验3.2.2 固定隐层矩阵大小(bsize),探索本文算法不同节点数(nodes)的分类能力.见图3.本实验选取的节点数为100、150或200、300、400.通过图3发现,在一定范围内,测试精度随着隐层节点数的增加而增加.但也不是绝对的,如FERET数据库,随着隐层节点数的增加,它的测试精度反而下降了.原因是节点数过多,容易造成过拟合.

实验3.2.3 固定隐层节点数(nodes), 探索本文算法隐层矩阵大小(bsize)的分类能力.见图4.

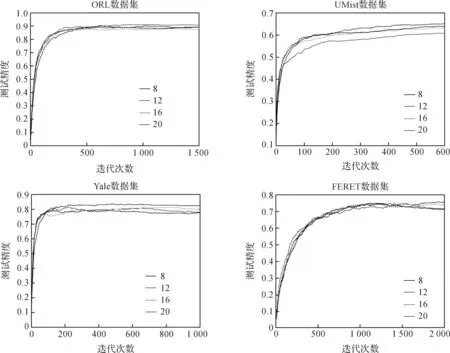
图4 第二隐层矩阵不同大小的测试精度对比Figure 4 Testing comparison of different matrix sizes in the second hidden layer

本实验隐层矩阵大小为8、12、16、20.从图4可发现,随着隐层矩阵变大,测试精度并没有增加,而是稳定在一定范围内变动.通过实验可以看出,UMist、Yale和FERET数据库的隐层矩阵大小在bsize=8时取得了最好效果,表明隐层矩阵的设置不宜过大.

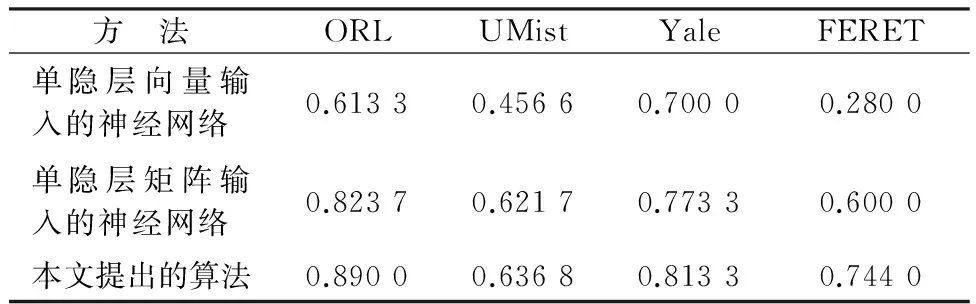
表1 多个数据库中不同算法的测试精度比较

4 结 语

本文在单隐层矩阵输入的神经网络的基础上,提出了多层矩阵输入的神经网络,并将此网络应用于图像分类中.通过与单隐层矩阵输入的神经网络的实验对比,验证了本文算法具有更高的识别率.通过固定隐层节点数或隐层矩阵大小,还探索了本文算法的内在关系.

[1] ROSENBLATT F. The perceptron: A probabilistic model for information storage and organization in the brain[J].Psychologicalreview,1958,65(6):386-408.

[2] WERBOS P J. Generalization of backpropagation with application to a recurrent gas market model [J].NeuralNetworks, 1988, 1(4):339-356.

[3] OOYEN A V, NIENHUIS B. Improving the convergence of the back-propagation algorithm [J].NeuralNetworks, 1992, 5(3):465-471.

[4] ZHANG Y, PHILLIPS P, WANG S, et al. Fruit classification by biogeography-based optimization and feedforward neural network[J].ExpertSystemstheJournalofKnowledgeEngineering, 2016, 33(3):239-253.

[5] BROWN W M, GEDEON T D, GROVES D I, et al. Artificial neural networks: A new method for mineral prospectively mapping [J].AustralianJournalofEarthSciences, 2015, 47(4):757-770.

[6] 杨凯杰,章东平,杨力.深度学习的汽车驾驶员安全带检测[J].中国计量大学学报,2017,28(3):326-333

YANG K J, ZHANG D P, YANEG L .Safety belt detection based on deep learning[J].JournalofChinaUniversityofMetrology, 2017,28(3):326-333.

[7] HANBURY A. A survey of methods for image annotation [J].JournalofVisualLanguagesandComputing, 2008, 19(5): 617-627.

[8] CHAN T H, JIA K, GAO S, et al. PCANet: A simple deep learning baseline for image classification?[J].IEEETransactionsonImageProcessingAPublicationoftheIEEESignalProcessingSociety, 2015, 24(12):5017-5032.

[9] KIRBY M, SIROVICH L. Application of the Karhunen-Loeve procedure for the characterization of human faces [J].IEEETransactionsonPatternAnalysis&MachineIntelligence, 2002, 12(1): 103-108.

[10] STONE J.PrincipalComponentAnalysisandFactorAnalysis[M]. Massachusetts:MIT Press,2004:129-135.

[11] OS A N. Face recognition using LDA-based algorithms [J].IEEETransactionsonNeuralNetworks, 2003, 14(1):195-200.

[12] ZHENG W S, LAI J H, YUEN P C.GA-fisher: A new LDA-based face recognition algorithm with selection of principal components [J].IEEETransactionsonSystemsMan&CyberneticsPartB, 2005, 35(5):1065-1078.

[13] KOTHARI S C,HEEKUCK O. Neural networks for pattern recognition [J].AdvancesinComputers,1993,37(1):119-166.

[14] RIPLEY B D. Pattern recognition and neural networks[J].Technomet-rics, 2008, 39(2):233-234.

[15] CHIEN J T, WU C C. Discriminant waveletfaces and nearest feature classifiers for face recognition [J].IEEETransactionsonPatternAnalysis&MachineIntelligence, 2002, 24(12):1644-1649.

[16] HUANG K, AVIYENTE S. Wavelet feature selection for image classification [J].IEEETransactionsonImageProcessing, 2008, 17(9):1709-1720.

[17] HU H. Variable lighting face recognition using discrete wavelet transform[J].PatternRecognitionLetters, 2011, 32(13):1526-1534.

[18] DAI K, ZHAO J, CAO F. A novel algorithm of extended neural networks for image recognition [J].EngineeringApplicationsofArtificialIntelligence, 2015, 42(C):57-66.

[19] SCHMIDT W F, KRAAIJVELD M A, DUIN R P W. Feedforward neural networks with random weights[C]//IAPRinternationalconferenceonpatternrecognition,conferenceB:Patternrecognitionmethodologyandsystems. New York: IEEE, 1992: 1-4.

[20] LU J, ZHAO J, CAO F. Extended feed forward neural networks with random weights for face recognition [J].Neurocomputing, 2014, 136(1):96-102.

[21] IGELNIK B,PAO Y H. Stochastic choice of basis functions in adaptive function approximation and the functional-link net [J].IEEETransactionsonNeuralNetworks, 1995, 6(6):1320-1329.