基于时频分析的混沌噪声背景下谐波信号频率估计

孙海欣，佐藤礼华

(1. 长春大学 电子信息工程学院， 长春 130022;2.大阪电气通信大学 综合信息学院，大阪 5408570)

0 前言

自从混沌现象受到关注以来，混沌信号已被证实广泛存在于大自然中，在气象、水文、通信等多个领域都有着广泛的应用[1]。信息在实际传输与交换的过程中，均通过信号这一物理实体来实现。由于产生信号的设备本身和信号的传输环境往往具有随机性，传输的信号中会出现附加噪声和干扰，呈现出传输信号和混沌噪声相混合的复杂信号，必须对其加以处理，才能提供给信息接收者使用。因此，必须有针对性地对混沌噪声和白噪声进行抑制，才能有效地提取传输信号的相关信息及参数。

本文采用由正交小波构造思想出发所构造的Daubechies小波和相关法相结合对淹没在混沌噪声背景下的谐波信号的频率进行估计。该方法利用周期信号和混沌噪声信号在小波不同尺度分解具有不同能量聚集性的特点，对混沌噪声信号进行削弱，再利用周期信号的自相关特性，即当时延为信号周期整数倍时，周期信号的自相关函数也具有周期性的特点对周期信号的频率进行提取。以谐波信号为例，对混沌背景下的谐波信号频率进行估计。

1 相关法和Daubechies小波变换

1.1 相关法

假设被测周期信号为s(t)，在传输过程中引入混沌噪声n(t)，s(t)和n(t)相互独立。x(t)为谐波信号和混沌噪声的混合，其形式如式(1)所示。

x(t)=s(t)+n(t)。

(1)

x(t)的自相关函数为：

Rx(τ)=E[x(t)x(t-τ)]=E{[s(t)+n(t)][s(t-τ)+n(t-τ)]}=Rs(τ)+Rn(τ)+Rsn(τ)+Rns(τ)。

(2)

由于n(t)和s(t)相互独立，假设n(t)的均值等于零，则Rsn(τ)=Rns(τ)=0，式(2)可简化为：

Rx(τ)=Rs(τ)+Rn(τ)。

(3)

根据周期信号的性质可知：周期信号的自相关函数仍为周期函数，且周期与周期信号的周期相同。设周期信号的周期为T，当τ=0或τ=T时，s(t)的自相关函数Rs(τ)取得最大值；而对于均值为零的非周期性混沌噪声n(t)，其自相关函数Rn(τ)仅在τ=0时取得最大值，但当τ逐渐变大时，Rn(τ)逐渐衰减至零。因此，对于含有混沌噪声的周期信号x(t)，当τ为T的整数倍时，自相关函数Rx(τ)仅仅体现Rs(τ)的变化情况，根据此性质即可估计出淹没在混沌噪声背景下的周期信号的频率。

若引入的混沌噪声均值不为零，则需要对噪声进行均值零化处理，即根据：

E[x(t)+m]=E[x(t)]+m,m为常数

(4)

将式(1)变形为：

x(t)=s(t)+[n(t)-m]。

(5)

式中，m为噪声的均值。式(5)保证了混沌噪声的均值等于零。此时利用式(3)，即可从混合信号的自相关函数Rx(τ)中估计出周期信号s(t)的频率[8]。

1.2 Daubechies紧支集正交小波变换

根据小波变换理论可知，正交小波分解具有良好的性质。可利用Mallat算法实现正交小波分解与重构的便捷递推算法。本文采用Daubechies小波来构造正交小波，该小波具有光滑性，可以高精度地模拟和分析信号，并且具有很强的时域和频哉局部化能力，Daubechies小波的构造原理如下：

紧支集标准正交尺度函数φ(t)满足：

(6)

其中，M为有界正整数，H(ω)是周期函数，其周期为2π。H(ω)2近似为周期函数，其周期同样为2π，且H(ω)2具有偶对称性。从滤波器的通带特性来看，H(ω)2具有低通特性，H(ω+π)2具有高通特性，H(ω)2和H(ω+π)2之和等于1。

由于H(ω)2是以2π为周期的偶对称函数，用余弦级数形式可表示成：

(7)

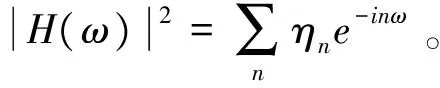
(8)

由于H(ω)2具有偶对称性，其Fourier展开系数ηn也具有偶对称性。对式(8)进一步改写为：

(9)

结合式(7)与式(9)，得出M=N，推导出H(ω)2的两种表示形式，分别如式(10)和式(11)所示：

(10)

(11)

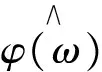
2 混沌噪声背景下谐波信号的频率估计

根据混沌信号的特性可知：混沌噪声n(t)的能量主要集中在低频段，而实际待测的谐波信号s(t)的频率相对较高。根据两种信号的频率成分不同的特点，实现混沌噪声和谐波信号的分离，从而有效估计出谐波信号的频率。本文利用小波变换法和相关法相结合对混沌噪声背景下谐波信号的频率进行估计，该方法的基本原理是对被测信号x(t)进行小波分解，利用混沌噪声与谐波信号在不同的分解尺度上具有不同的能量聚集性的特点，通过采取不同的尺度系数对含有混沌噪声的谐波信号进行Daubechies小波重构，可将混沌噪声和谐波信号分离。再利用相关法进一步计算，即可估计出谐波信号的频率。算法的具体步骤为：

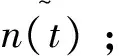
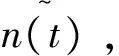
根据小波多尺度分解理论可知，N不同时，小波分解后的能量聚集特性不同。N越大，多尺度分解时滤波器的长度越长，滤波性能越好，但会导致时域定位性能恶化。对被测信号x(t)进行小波分解和重构时，对于不同类型的混沌噪声，N的长度各不相同。本文通过仿真验证，选取N=5 进行Daubechies小波分解。

本文通过信噪比来衡量Daubechies小波分解与重构前后，对混合信号x(t)中混沌噪声n(t)的抑制程度，信噪比定义为：

(13)

3 仿真实验及结果分析

本文假设混沌噪声信号为Lorenz系统输出的信号，Lorenz系统方程满足：

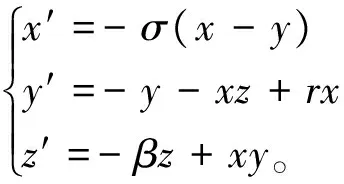
(14)

式中δ=10，ρ=28，β=8/3。

(15)

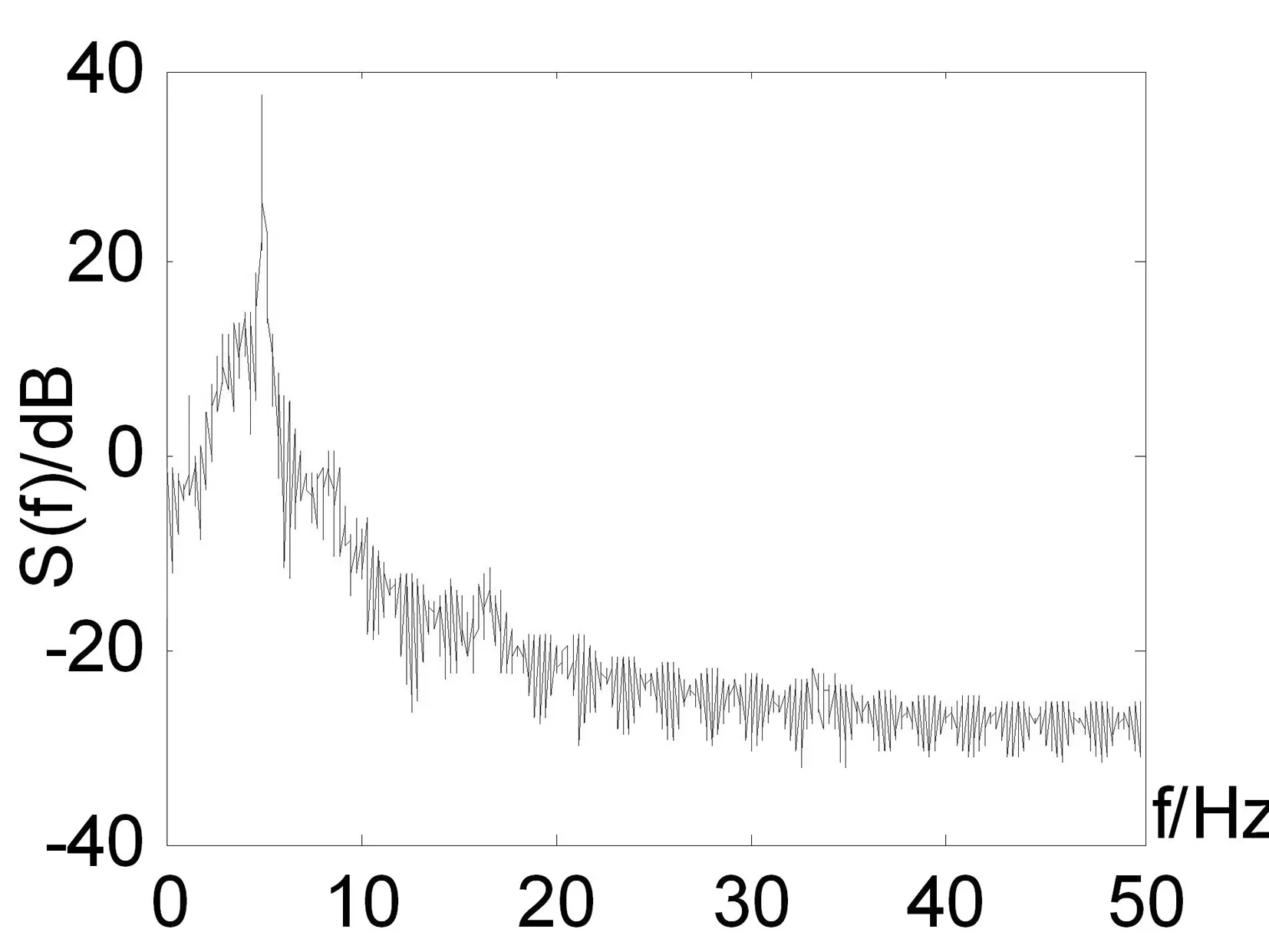
图1 估计出的谐波信号频率

在下面的仿真实验中，采用四阶龙格-库榙算法产生长度为5000的混沌噪声数据，步长为0.01，Lorenz信号初值为x0=y0=z0=1，采样频率为100Hz。

实验1：混沌噪声背景下谐波信号的频率估计。

假设n=1，A=5，f=5Hz，利用小波变换法和相关法相结合对Lorenz混沌噪声背景下谐波信号的频率进行估计，估计后的频谱仿真结果如图1所示。

保持谐波信号频率f=5Hz不变，当幅度A变化时，谐波信号和混沌噪声的信噪比变化如表1所示。根据表1的结果可知，当谐波信号的频率f固定不变，信噪比与谐波信号的幅度呈正比关系。

表1 谐波信号幅度与信噪比的关系

实验2：混合噪声背景下谐波信号的频率估计。

谐波信号参数为n=3，A1=3，f1=5Hz，A2=4，f2=7Hz，A3=5，f3=3Hz，淹没在白噪声和混沌噪声构成的混合噪声背景下，混合信号波形如图3所示。从图2中看不出任何谐波信息。利用小波变换法和相关法相结合，对混合信号进行频率估计，混合信号的自相关函数如图3所示，频谱仿真结果如图4所示。由图4可以看出，谐波信号的3个频率被准确的估计出来。

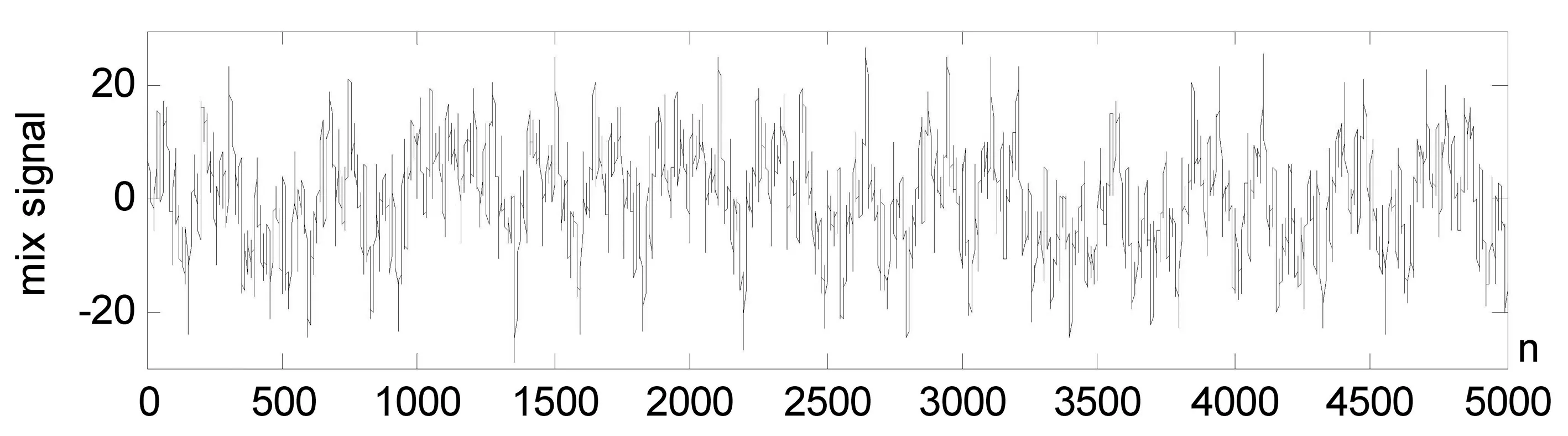
图2 混合噪声背景下的谐波信号波形图

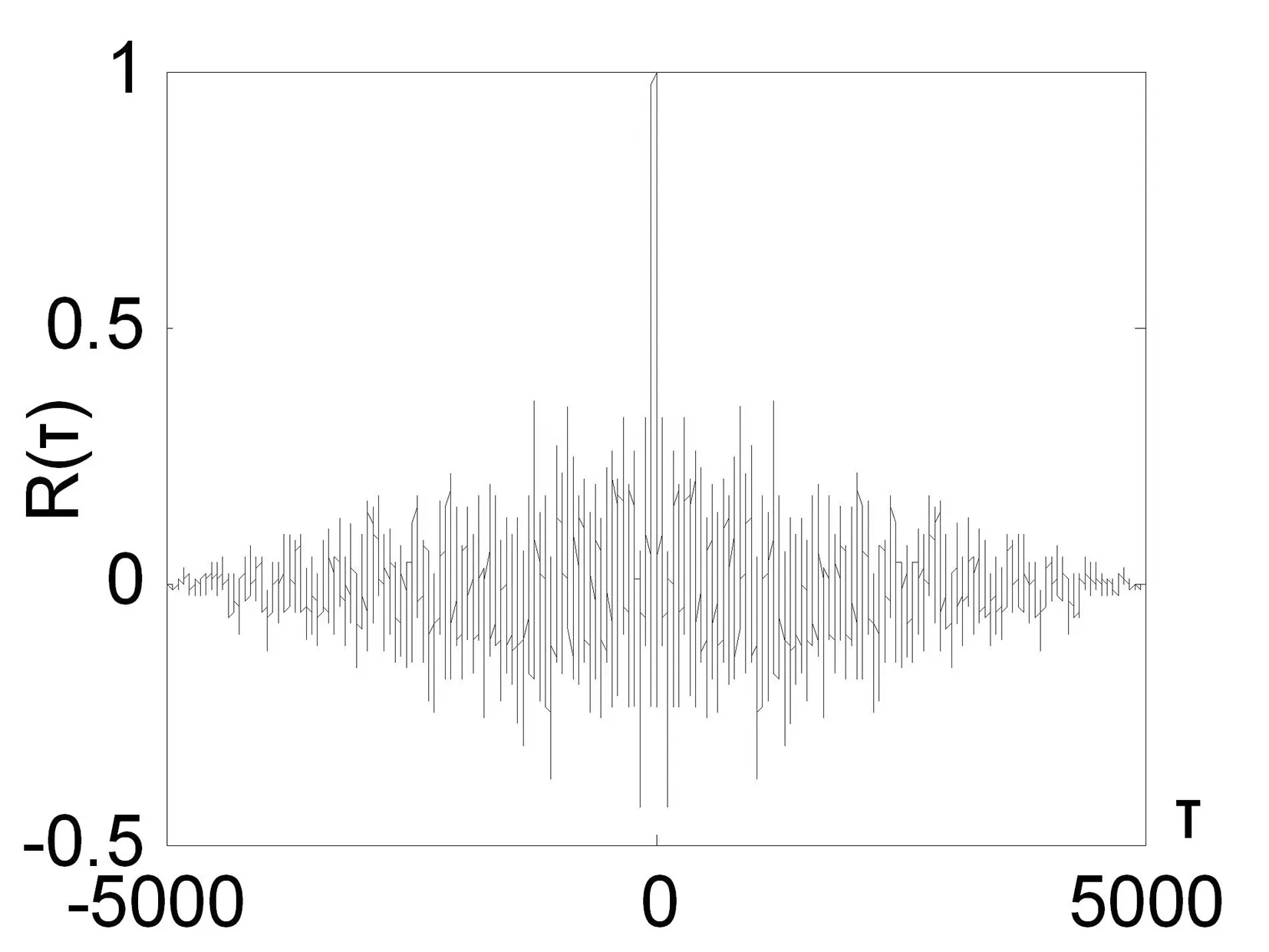
图3 混合信号的自相关函数

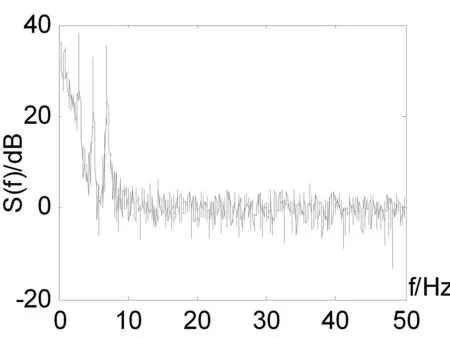
图4 估计出的谐波信号频率

4 结语

本文提出了一种基于小波变换法和相关法结合的方法对混沌噪声背景下谐波信号的频率进行估计。根据谐波信号和混沌噪声的自相关性不同以及在小波分解的不同尺度上的能量不同聚集性的特点，对混沌噪声进行抑制，从而有效估计出谐波信号的频率。该方法不需要对混沌噪声信号的相空间进行重构，计算量小，易于实现。理论分析和仿真实验表明，在信噪比较低的情况下，本文提出的方法能有效地估计出谐波信号的频率，具有良好的抗噪性和实用价值。

[1] 吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2002.

[2] 姜斌. 海杂波建模及目标检测技术研究[D].长沙：国防科学技术大学,2006.

[3] 许小可. 基于非线性分析的海杂波处理与目标检测[D].大连：大连海事大学,2008.

[4] 王国光,王树勋,何丽桥.强混沌和噪声背景下微弱信号的检测[J].吉林大学学报(工学版)，2016，36(S1)：116-121.

[5] Huang X G, Xu J X.Unmasking chaotic mask by a wavelet multiscale decompositionalgorithm[J]. Int.J.Bif & Chaos,2011,11(2):561.

[6] 李鸿光,孟光.基于EMD方法的混沌信号中周期分量的提取[J].应用数学和力学,2006,27(2):199-203.

[7] 李鸿光,孟光.基于经验模式分解的混沌干扰下谐波信号的提取方法[J].物理学报,2004,53(7):2069-2073.

[8] 孙海欣. 混沌噪声背景下周期信号的频率估计的方法研究[D].长春：吉林大学, 2008.