基于Simulink的伺服缸新型支撑结构控制系统仿真研究

马强俊，黄庆学,2，马丽楠，和东平

(1.太原科技大学 重型机械教育部工程研究中心，太原 030024；2.太原理工大学 机械工程学院，太原 030024)

大型重载伺服液压缸是伺服控制系统的关键元件，也是液压滚切剪机的核心设备，其性能的好坏严重影响着伺服缸的使用寿命以及滚切剪机的生产效率[1-3]。在滚切剪机上，伺服缸需卧式铰接安装，输出曲线力，旋转一定的角度，但是，由于缸筒自身重力的影响，会引起拉缸、泄漏以及输出力减小等不良反映，为了解决这些问题，提出一种在伺服缸端底铰接一个支撑小缸的新型支撑结构以及配套的外接液压控制系统。该控制系统是新型支撑结构的核心，可以精确控制支撑小缸的压力和位移，使其保证伺服缸的活塞杆全程无摩擦运行，进而改善伺服缸性能，以满足实际工况。

目前，国内外许多学者在压力和位置同步精确控制研究方面取得了显著成就[4-7]。MADANI et al[8]在外科手术中使用的医疗机械手，WELLS et al[9]在视网膜显微手术过程中的手持式机器人等方面成功实现了压力与位置的同步精确控制。谢苗等[10]提出的电液伺服位置与压力复合控制方法，王君等[11]提出的位置压力主从伺服控制系统，权龙等[12]提出的位置闭环在外，压力闭环在内的串并联复合控制策略等方法有效的提高了压力与位置同步控制的精确度与稳定性。

基于以上研究背景，本文设计了一种压力、位置双闭环独立PID控制系统，可以精确控制支撑小缸的压力和位移，使其保证伺服缸的活塞杆全程无摩擦运行，避免了由于伺服缸自身重量所引起的密封圈摩损、拉缸和泄漏等现象。通过对压力、位置控制系统耦合特性的分析和研究，进行解耦运算，推导出该系统的数学模型，并进行系统稳定性分析。运用MATLAB/Simulink进行控制仿真，验证该控制系统的可行性与可靠性，为新型支撑结构的工程应用提供了扎实的基础。

1 新型结构控制原理

滚切剪机上卧式铰接安装的伺服缸在做工时，需输出曲线力并旋转一定的角度，针对这种工况，本文提出了一种在伺服缸端底铰接一个支撑小缸的新型结构，并配套了该结构的控制系统。通过对支撑小缸压力、位置的精确控制，实现了伺服缸活塞杆全程无摩擦运行，其工作原理如图1所示。

1-伺服缸；2-支撑小液压缸；3-比例换向阀；4-比例溢流阀；5-控制器；6-液压泵；7-联轴器；8-电动机；9-压力传感器；10-位移传感器图1 新型结构控制原理图Fig.1 Schematic diagram of new structure control

该伺服控制系统通过对压力和位置的自适应调整，使伺服缸的活塞杆始终悬浮在缸盖导向套中，实现全程无摩擦运行，避免由于缸筒自身重量所引起的拉缸、泄漏以及输出力不足等现象。通过控制器对压力和位移传感器的反馈数据进行及时处理，分别实时控制比例溢流阀与比例换向阀，对支撑小缸的输出力及位置进行精确控制，从而控制活塞杆始终悬浮在缸盖导向套中，避免由于伺服缸缸筒自身重量引起的不利影响，达到一个动态平衡。

2 模型建立与稳定性分析

2.1 控制系统的耦合关系

根据控制系统原理可知，压力、位置双闭环系统存在着一定的耦合特性，使得压力、位置难以独立控制，因此需要进行解耦。通过对控制系统原理的分析，得到如图2的耦合系统框图。

图2 压力位置耦合关系框图Fig.2 Coupling relation of pressure and position

压力闭环控制系统是通过支撑小缸无杆腔的压力传感器将检测到的压力信号与给定信号反馈给PID控制器，实时控制比例溢流阀，通过比例换向阀压降后，使其输出给定力。位置闭环控制系统是通过位移传感器将检测到的位移信号与给定信号反馈给PID控制器，实时控制比例换向阀，使其输出适量的液压流量来控制液压缸活塞杆的位移，与此同时，压力的变化也会对位移造成一定的影响。

2.2 建立数学模型

比例溢流阀是压力闭环控制系统的核心元件，其数学模型比较复杂，为了便于分析研究，将其简化为二阶系统模型[13]。

(1)

式中：ω1为比例溢流阀固有频率，ξ1为比例溢流阀阻尼比。

由于活塞杆伸出与缩回运动类似，下面只做活塞杆伸出阶段的比例换向阀压降计算。

(2)

式中：Δp为比例换向阀总压降；ps为进油压力；p1为无杆腔压力；p2为有杆腔压力；Q1、Q2分别为比例换向阀进、出油流量；a1、a2分别为进、回阀口开启面积。

由一些相互关系可得：

(3)

式中:A1为无杆腔有效面积；A2为有杆腔有效面积；k为进、回阀口开启面积比值。

由式(2)、式(3)得:

(4)

由力平衡得：

p1A1=p2A2+F.

(5)

式中：F为外负载力。

由式(4)、式(5)得：

p1=k1ps+k2F.

(6)

令p2=0，则得比例换向阀压降比例环节：

p1=k3ps.

(7)

比例换向阀是位置闭环控制系统的核心元件，其模型十分复杂，为了便于分析研究，将其简化为二阶系统模型[14]。

(8)

式中：kq为流量增益，ω2为比例换向阀固有频率，ξ2为比例换向阀阻尼比。

阀控缸位移的数学模型比较复杂，为了便于分析，将其简化为[15]：

(9)

式中：ωh为液压缸的固有频率，ξh液压缸的阻尼比。

压力变化对位移的影响，根据力平衡公式可得：

(10)

通过对式(10)进行拉氏变化可得：

(11)

由以上的分析可以得到如图3所示的双输入双输出系统耦合框图。

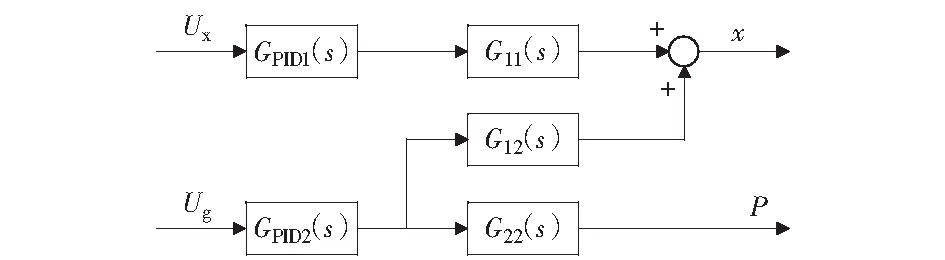
图3 系统耦合框图Fig.3 System coupling diagram

图中GPID1(s)为位置闭环PID控制器，GPID2(s)为压力闭环PID控制器。

位置闭环的控制对象传递函数为：

(12)

压力变化对位移的影响的传递函数为：

(13)

压力闭环的控制对象传递函数为：

(14)

2.3 解耦运算

本文采用前馈解耦来解除多变量系统的耦合性，简化解耦控制系统框图如图4.

图4 简化解耦控制系统框图Fig.4 Decoupling control system diagram

其中N(s)为解耦装置矩阵，由简化解耦控制系统可得：

(15)

由于解耦矩阵须为对角矩阵，则：

(16)

由式(15)、(16)可得解耦矩阵模型为：

(17)

解耦后的广义对象模型为：

(18)

通过对位置闭环控制系统分析与研究，可知比例换向阀的固定频率ω2=2.1 rad/s，比例换向阀的阻尼比ξ2=0.7，液压缸的固定频率ωh=370 rad/s，液压缸的阻尼比ξh=0.2，无杆腔的有效面积A1=0.007 85 m2，流量增益kq=0.037.将其代入式(12)得：

(19)

通过对压力变化对位移的影响的分析和研究，可知m=11 kg，Bp=2×105kg/s.将其代入式(13)得：

(20)

(21)

由式(17)—(21)可得：

(22)

(23)

2.4 稳定性分析

由以上解耦运算可得到压力和位置独立闭环的控制对象线性化模型，运用李雅普诺夫第二法对压力和位置闭环分别进行稳定性分析。通过对控制系统的研究可知压力传感器增益kp=0.42，位移传感器增益kx=0.2.

压力闭环控制系统传递函数为：

(24)

由传递函数可以得压力闭环控制系统的自治方程为：

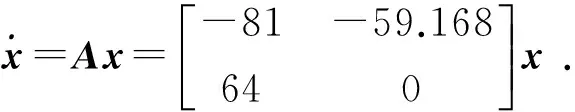
(25)

取正定二次函数V(x)=xTHx作为可能的李雅普诺夫函数，则：

(26)

只要ATH+HA正定，就可以判定系统是大范围渐进稳定的。令

ATH+HA=-E.

(27)

式中：E为单位矩阵。

只要判定H为正定矩阵，就可以得到ATH+HA为正定，设判定矩阵

(28)

通过计算可得：

(29)

由式(29)可知是H正定矩阵，因此可得该压力闭环控制系统为稳定系统。

位置闭环控制系统传递函数为：

(30)

同样，采用李雅普诺夫第二法对其进行稳定性分析，得判定矩阵：

(31)

由于D是正定矩阵，因此可得该位置闭环控制系统为稳定系统。

3 控制仿真

为了进一步验证该控制系统的合理性和稳定性，运用MATLAB/Simulink进行仿真控制，在Simulink上搭建压力闭环与位置闭环的控制仿真模型如图5、图6所示。

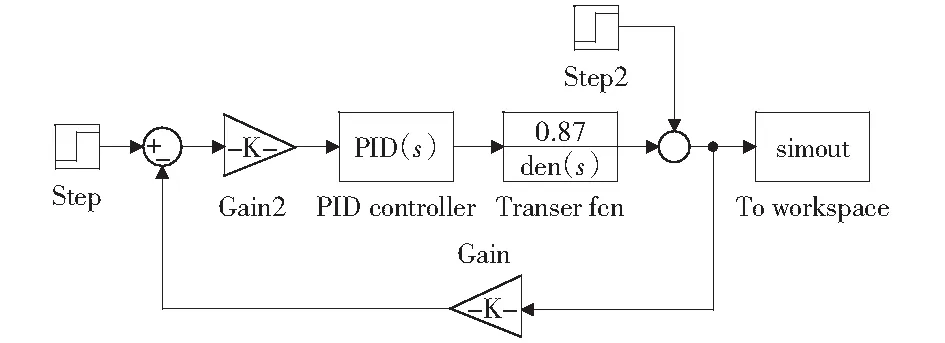
图5 压力闭环控制仿真Fig.5 Simulation of pressure closed loop control

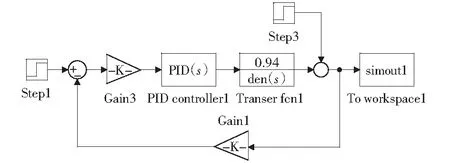
图6 位置闭环控制仿真Fig.6 Simulation of position closed loop control

为了验证该控制系统的跟踪性能以及抗干扰能力，在0 s时给予压力闭环控制系统与位置闭环控制系统单位阶跃信号，并在4 s时加入幅值为0.1的阶跃干扰信号。压力闭环控制系统的PID值分别为：2.1，0.02，0；位置闭环控制系统的PID值分别为：2，0.2，0.01，其仿真结果如图7、图8所示。

通过图7和图8可以看出，压力信号与位置信号跟踪性能良好，抗干扰能力强。由压力阶跃信号响应图7的局部放大图可以看到，在压力上升的瞬间产生微小振荡，在0.1 s后跟踪给定值，同样在4 s时加入干扰信号时，0.1 s后跟踪给定值，压力闭环控制系统实现了快速稳定跟踪给定值。由位置阶跃信号响应图8可以看出，位置信号可以快速无超调的达到跟踪给定值，在4 s时加入干扰后，很快能够跟踪到给定值。该仿真结果验证了压力、位置双闭环独立PID控制系统的合理性与可靠性。

图7 压力阶跃信号响应图Fig.7 Response diagram of pressure step signal

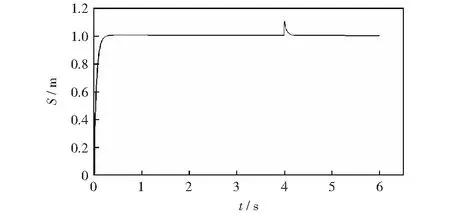
图8 位置阶跃信号响应图Fig.8 Response diagram of position step signal

4 实验验证

为了验证压力、位置双闭环独立PID控制系统的可行性与可靠性，搭建试验台，并对规格为Ø100/80-250的支撑小缸作为执行机构的液压控制系统进行现场测试。其中比例溢流阀型号为RZMO-P1ES-PS-010/315/1，比例换向阀型号为4WRDE16-125L-5X/6L24K9/M，液压泵的型号为EOS4VSO125OR/30R-PPB13U34，排量为125 mL/r，伺服缸的规格为Ø360/220-400，压力传感器型号为HDA3840-A-400-000，位移传感器的型号为RHM0420MD701S2G1102.

通过对新型结构的动力学研究，可知活塞杆往返全程运行8.4 s，前4 s为匀速伸出阶段，4 s后为匀速返程阶段，小缸的输出力曲线模型为：

(32)

式中：F为给定输出力函数曲线；s为给定位移函数曲线；G、m1分别为卧式伺服缸缸筒重量、质量；a为缸筒质点的切向加速度；θ为卧式缸的旋转角。

通过现场测试，结果得到如图9、图10所示。

图9 位移测试结果图Fig.9 Results of displacement test

根据位移测试结果图9可以看出，位置控制系统基本实现了快速稳定跟踪给定信号，其误差在0.004 m以内，达到了新型结构位置精确跟踪的工况需求。通过输出力测试结果图10可以看到，在前4 s的活塞杆在伸出阶段，实际输出力稳定跟踪给定值，达到了工况需求。在4 s后的活塞杆返程阶段，由于有杆腔压力变大，导致无杆腔背压增大，使实际输出力变大，其误差在3.8%以内，这是预测范围之内的，对实验结果不会造成影响。

图10 输出力测试结果图Fig.10 Results of output force test

通过实验验证了压力、位置双闭环独立PID控制系统的可行性与可靠性，实现了力与位置独立控制，为伺服缸端底铰接一个支撑小液压缸的新型结构提供了可靠的现实依据。

5 结论

由仿真试验结果可以看出，基于伺服缸端底铰接一个支撑小缸的新型结构的压力、位置双闭环独立PID控制系统设计是可行的，可以实现小缸压力与位置同步精确控制，使伺服缸活塞杆全程无摩擦运行，其误差在可以接受的范围之内。通过在伺服缸端底铰接一个支撑小缸的新型结构及其控制系统，有效的改善了滚切剪机伺服缸的工况，为解决类似问题提供了一定的依据，具有较高的应用价值。

[1] 马立峰,黄庆学,韩贺永,等.驱动复合连杆机构滚动的液压控制系统特性[J].北京工业大学学报,2012,38(11):1601-1607.

MA L F,HUANG Q X,HAN H Y,et al.Characteristics of hydraulic control system for using driving the composite connecting rod mechanism Rolling[J].Journal of Beijing University of Technology,2012,38(11):1601-1607.

[2] 楚志兵,黄庆学,马立峰,等.滚切式双边剪连杆机构的动力学仿真及实验研究[J].四川大学学报(工程科学版),2011,43(1):247-252.

CHU Z B,HUANG Q X,MA L F,et al.Experimental study and simulation of kinetics on linkage structure of rolling-cut bilateral shear[J].Journal of Sichuan University (Engineering Science Edition),2011,43(1):247-252.

[3] JIAN F M,WEI Z W,YING Z L.Experimental and theoretical investigation on the sealing performance of the combined seals for reciprocating rod[J].Journal of Mechanical Science and Technology,2012,26(6) :1765-1772.

[4] YAO J,LI B,KONG X D,et al.Displacement and dual-pressure compound control for fast forging hydraulic system[J].Journal of Mechanical Science and Technology,2016,30(1):353-363.

[5] JUN J P,JIN X,POTT A,et al.Hybrid position/force control using an admittance control scheme in Cartesian space for a 3-DOF planar cable-driven parallel robot[J].International Journal of Control,Automation and Systems,2016,14(4):1106-1113.

[6] 高炳微,邵俊鹏,韩桂华.电液伺服系统位置和力模糊切换控制方法[J].电机与控制学报,2014,18(5):99-104.

GAO B W,SHAO J P,HAN G H.Fuzzy switching control between position and force for electro-hydraulic servo system[J].Electric Machines and Control,2014,18(5):99-104.

[7] YANOU A,MINAMI M,TANIMOTO H.Continuous shape-grinding experiment based on model-independent force/position hybrid control method with on-line spline approximation[J].Artificial Life and Robotics,2013,18(3/4):219-227.

[8] MADANI M,MOALLEN M.Hybrid position/force control of a flexible parallel manipulator[J].Journal of the Franklin Institute,2011,348(6):999-1012.

[9] WELLS T S,YANG S,MACLACHLAN RA,et al.Hybrid position/force control of an active handheld micromanipulator for membrane peeling[J].Int J Med Robot,2016,12(1):85-95.

[10] 谢苗,刘治翔,池城,等.巷道超前支架的电液伺服位置压力复合控制方法[J].中国机械工程,2016,27(2):239- 245.

XIE M,LIU Z X,CHI C,et al.Electro-hydraulic servo position and pressure hybrid control method of fore poling system on tunneling[J].China Mechanical Engineering,2016,27(2):239-245.

[11] 王君,黄庆学,安高成,等.液压滚切剪机位置压力主从控制的研究[J].流体传动与控制,2015(5):5-10.

WANG J,HUANG Q X,AN G C,et al.Research on position-pressure master-slave control of rolling shear hydraulic system[J].Fluid Power Transmission & Control,2015(5):5-10.

[12] 权龙,许小庆,李敏,等.电液伺服位置、压力复合控制原理的仿真及试验[J].机械工程学报,2008,44(9):100-105.

QUAN L,XU X Q,LI M,et al.Simulation and test electro-hydraulic servo position and pressure hybrid control principle[J].Journal of Mechanical Engineering,2008,44(9):100-105.

[13] 王传礼,丁凡,殷建立,等.卷染机电液张力控制系统的动态特性研究[J].浙江大学学报(工学版),2004,38(5):631-635.

WANG C L,DING F,YIN J L,et al.Reseach on dynamic characteristics of jigger electro-hydraulic tension control system[J].Journal of Zhejiang University (Engineering Science),2004,38(5):631-635.

[14] 李胜,阮健,孟彬.二维电液比例换向阀动态特性及稳定性分析[J].机械工程学报,2016,52(2):202-212.

LI S,RUAN J,MENG B.Two-dimensional electro-hydraulic proporti onal directional valve[J].Journal of Mechanical Engineering,2016,52(2):202-212.

[15] 陈柏金,徐明昊,张红颖.液压锻造操作机大车行走机构的位置控制系统[J].华中科技大学学报(自然科学版),2011,39(8):7-9.

CHEN B J,XU M H,ZHANG H Y.Position control system for hydraulic forging manipulator cart movement mechanism[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2011,39(8):7-9.