平底筒仓中物料颗粒流动特性研究

牛雪梅，孟文俊，王爱红

(太原科技大学 机械工程学院，太原 030024)

由于筒仓是用于储存各种不同颗粒物料的容器，故其结构的安全性需要重点考虑，对此除了了解物料施加在筒仓壁的压力[1-2]，筒仓外加载荷[3-4]以及筒仓可能出现的事故[5-6]等方面外，还需要了解在卸载物料时对其产生影响的因素，如筒仓卸料方式[7-8]，筒仓中物料流动形态[9-10]，筒仓中物料流动速度和卸料率[11-12]等。筒仓的分类方式众多，其中最常见的是按筒仓底部形状将筒仓分为锥形底和平底筒仓，它们被广泛应用在工农业生产中，用来储存如煤，粮食等物料。

文献[13]研究了锥形漏斗筒仓自由流动时，卸料口出现堵塞时卸料率数学式和卸料口流动速度分布。文献[14]通过实验和DEM仿真分析了滚动摩擦对物料自由流动速度的影响，滚动摩擦减小了颗粒的水平速度，减小了NEDDERMANAND and TÜZÜN(1979)所提出的描述颗粒速度公式中的B值。文献[15]利用SIELAMOWICZ et al建立的实验，通过统计分析方法，用径向速度假设，抛物线函数和高斯函数对物料在筒仓中的自由流动现象进行了描述。文献[16]使用DEM仿真软件，研究颗粒尺寸，漏斗筒仓半顶角，摩擦系数和筒仓高度等参数对物料自由流动速度的影响。文献[17]主要使用有限元仿真卸料过程中锥形漏斗底筒仓壁的压力波动变化的影响因素发现，卸料速度减小，筒仓壁的压力波动幅度和频率都会减小。文献[18]使用DPIV方法测量筒仓中自由流动颗粒的速度值，并对3种垂直速度理论模型：运动学模型，经验运动学模型(及修改的经验运动学模型)和抛物线函数模型进行比较分析指出，抛物线函数较好地描述了速度的分布特性。文献[19]使用仿真和实验的方法研究平底和锥形底漏斗筒仓中放置改流体引起流动速度、卸料率以及筒仓壁所受压力发生的变化。

从以上文献看出，许多学者研究了锥形底筒仓，而且相关文献大多都是物料在锥形底筒仓中自由流动的情况，对于平底筒仓，尤其是配置有螺旋输送机封闭式大型平底筒仓的物料流动特性几乎鲜有研究。 本文主要研究平底筒仓中自由流动物料颗粒速度，以及有螺旋输送机辅助卸料下物料颗粒速度的变化情况，为大型平底筒仓中物料流动和筒仓结构分析提供理论依据。

1 大型封闭筒仓概述及相关研究理论

国外早在20世纪60年代就由ESI Eurosilo公司建造了全新的封闭储存系统——第一台大型平底筒仓，也称为猛犸仓。平底筒仓工作原理和平底筒仓结构如图1所示。

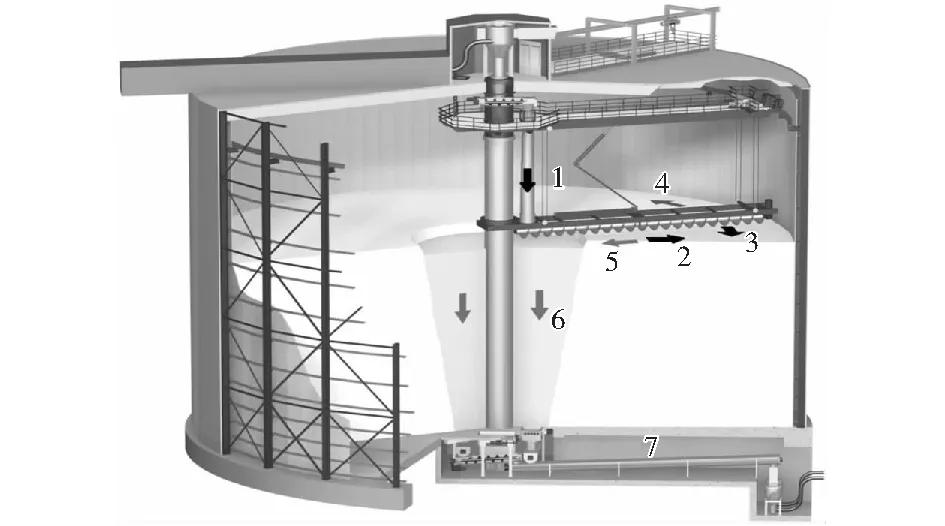
图1 ESI Eurosilo BV的猛犸仓运行示意图[20]Fig.1 Operational scheme of a mammoth silo of ESI Eurosilo BV[20]

物料从大型平底筒仓的顶部填入，沿伸缩溜槽输送到螺旋输送机中(1)，物料从溜槽处被输送到筒仓壁处(2)，随着螺旋机叶片的自转和公转运动，将平底筒仓中已有的物料上(3)再铺上一层物料。铺满一层后，螺旋输送机提升，这样直到物料全部装满筒仓。当取料时，螺旋输送机反向转动(4和5)，把物料从筒仓壁处输送到筒仓中心，通过中心卸料区从平底筒仓中卸出(6)，最后，物料通过输送系统输送到加工设备处(7).

大型封闭式筒仓具有高效空间利用率，封闭系统有助于避免空气和土地污染。空间扩展性强，可以集成其他设备，实现自动化。

筒仓中物料流动时出现的问题，大多数与颗粒流动形态有关，它既影响了物料颗粒对筒仓壁的压力，也影响筒仓的结构。物料颗粒的流动形态大致可分为整体流和漏斗流；整体流是筒仓中全部物料整体流动，漏斗流是指筒仓卸料口上方中央处颗粒首先流动，随后其余部分颗粒流动。

比较简单的识别整体流和漏斗流的定量分析方法是MFI(mass flow index)[21],依据物料颗粒流动过程中速度场的分布特性，筒仓壁处速度与筒仓中心线处速度是不同的，即平行与筒仓壁的物料平均垂直速度与筒仓中心线处物料颗粒的平均垂直速度比值(aMFI)大小来确定，JOHANSON et al[22]给出了判定标准。如下式所示：

(1)

将aMFI的值为0.3作为整体流和漏斗流的分界点，当aMFI>0.3时为整体流，当aMFI<0.3时为漏斗流。

筒仓中物料流动速度预测的运动模型[23]，认为速度特性是与几何尺寸因素有关，而与应力分布无关。垂直速度分布为高斯分布，公式如下：

(2)

式中：v表示某点的速度；Q表示卸料率；y表示该点的高度；B表示常数系数，与颗粒直径有关；x是与垂直轴的距离。

离散单元法(DEM)是把离散体看成许多离散的独立运动单元，即每个颗粒作为一个单元，系统中的每一个颗粒都服从牛顿运动方程，交替反复运用牛顿运动定律来预测散体的整体运动形态，可以弥补实验中无法看到的物料流动内部现象，所以许多研究者使用DEM仿真软件研究筒仓中物料颗粒的流动情况,并得到了有效性和准确性的验证。如文献[24]使用DEM仿真了筒仓中自由流动物料的垂直速度分布，即式(2)表示的速度分布曲线，文献[25]用实验方法研究了式(2)表示的速度模型，与文献[24]研究完全一致。而本文使用EDEM中Hertz-Mindlin(No Slip)模型，该模型对力的计算比前人所使用的更加准确且高效。

2 仿真模型和参数

EDEM仿真软件中静态生成法生成筒仓中的颗粒[11]，筒仓中物料瞬时被整体填满在一个虚拟体积中，物料颗粒位置和方向随机产生，依重力下降，当所有下降颗粒静止后，装料过程结束。玉米颗粒分别由2，2.4 mm的两个圆球颗粒物拟合形成，圆球颗粒间距为0.8 mm.模拟颗粒物料特性[26-28]和筒仓尺寸如表1和图2所示.

表1 物料参数表Table 1 Property parameter of granule

图2 筒仓模型及尺寸坐标设置示意Fig.2 Schematic diagram of silo model and size coordinate

3 卸料过程的速度仿真分析

3.1 物料速度随时间变化对比分析

玉米物料颗粒生成后1.5 s时刻时，分别选取物料颗粒群表面筒仓壁的左、右以及中点位置处的3组颗粒，跟踪这些颗粒自由流动的垂直速度和径向速度。

自由流动的垂直速度分析如图3(a)，中间玉米颗粒垂直速度随时间变化逐渐增大，大约5 s左右颗粒逐渐靠近卸料口，阻碍该颗粒流动的下方物料减少，在重力作用下，进行纯自由落体运动，速度突然增大，进入快速颗粒流流动，将近6 s时，物料颗粒流出卸料口。中间物料颗粒垂直速度大于筒仓壁处物料颗粒垂直速度，也说明平底筒仓的流动形态是漏斗流。只是在卸料口开启的短暂时间内，筒仓上部出现整体流流动现象。

两边玉米颗粒沿着各自的滑移面流动，受到周围颗粒的碰撞和挤压，从筒仓壁两边向卸料口上方中心区域流动到大约6 s后，进入卸料漏斗区，也就是图中垂直速度出现波动区，由于进入卸料漏斗相对狭小的空间，物料颗粒速度碰撞，挤压作用频繁并且作用大，所以垂直速度出现波动。

自由流动的径向速度分析如图3(b)所示，文献[29]对此也进行了研究，并与本文研究结果相一致。在流动开始时间，玉米中间物料颗粒的径向速度小于筒仓两边颗粒的径向速度，这主要是两边颗粒从筒仓壁处流动到中心区域时，受到摩擦作用较大。中间颗粒从卸料口流出时，做自由落体运转，只有垂直速度，3～4 s间中间玉米颗粒出现垂直和径向速度突然增大的现象，随后又迅速降低，估计物料颗粒下落运动中相互碰撞，发生能量相互传递，期间该玉米颗粒突然受到其他颗粒的剧烈碰撞而出现不规律的运动现象。

图3 玉米速度随时间变化关系Fig.3 Change of velocity with time for corn

由上述自由流动颗粒垂直速度和径向速度分析可以看出，左右两边颗粒的流动趋势没有较大区别，故任意选取处于螺旋运动时，处于筒仓壁右边的颗粒进行螺旋辅助运行下的速度进行分析，如图4(a)所示。1.1 s后颗粒径向流动速度小于垂直流动速度，说明物料颗粒在此时刻前主要被螺旋输送机从筒仓壁处向中心卸料区输送，此时刻后物料流入到中心卸料区处，垂直速度增大，物料开始自由下落并快速流出卸料口。螺旋运动影响筒仓壁处物料颗粒的速度变化趋势。

任意选取中间颗粒速度分析得出，部分位于卸料口上方的颗粒以极快的速度从卸料口处流出，其余部分位于卸料口半径附近的颗粒因颗粒间的相互作用如图4(b)所示，一边径向移动一边垂直下落，大约在0.5 s时，径向速度增大，物料颗粒移动到卸料口上方处，随后从卸料口流出。通过对自由流动物料颗粒分析也得出相同的结果，由此看出螺旋运动对于中间颗粒的运动影响不大。

图4 玉米速度随时间变化Fig.4 Change of velocity with time for corn

3.2 物料垂直速度随高度变化对比分析

由玉米颗粒的垂直速度随高度变化图(如图5所示)分析可知，自由流动的中间物料颗粒随着逐渐趋近卸料口，垂直速度逐渐增大，在中心卸料区主要为垂直速度，并且流动较为稳定，只是在趋近卸料口上方时，进行自由落体运动，进入颗粒快速流阶段，速度增大。筒仓壁两边颗粒由于从两边流动到中心卸料区，在流动过程中颗粒间产生摩擦、碰撞、挤压等作用使得颗粒运动的速度会出现波动。右边玉米颗粒在筒仓高度为100 mm处垂直速度有突然增大现象，发生这种变化，可能是由于物料之间碰撞剧烈，使得这些颗粒吸收了巨大的能量，从而导致速度幅度大地变化，引起不规律的运动情况。

图5 玉米颗粒的垂直速度随高度变化(自由运动)Fig.5 Change of vertical velocity with height for corn(free flowing)

分析在螺旋输送机辅助运行下筒仓壁处颗粒的垂直速度和径向速度随高度变化(如图6(a)所示)。可知，由于筒仓壁处螺旋运动的表面颗粒随着螺旋输送机的转动而从筒仓壁处向中心卸料区运动，此时其径向速度大于垂直速度；随着物料颗粒不断地做螺旋运动，它将会从螺旋运动的表面不断向下做垂直运动。对于中间的玉米颗粒在运动开始时(如图6(b))，由于受到周围颗粒的相互制约，垂直和径向速度都较小。大约离筒仓底部7 mm左右处，物料颗粒的速度增大，尤其径向速度，使得物料颗粒快速流向卸料口处，并以较高的垂直速度流出卸料口。

图6 玉米颗粒的运动速度随高度变化Fig.6 Change of velocity with height for corn

3.3 物料垂直速度分布对比分析

研究不同高度上任一瞬时垂直速度场，分析自由流动时，不同高度的速度分布情况(如图7)，与式(2)表述的图形一致，也与文献[24-25]研究结果一致。同时利用MFI公式，计算出每条曲线的流动指数(如式(1)所示)及速度分布的弯曲度，以表明此位置的流动形态。图中aMFI值均小于0.3，图7(c)展示了相应彩色带图列。定量分析aMFI值并结合所观察到的流动形态可看出，玉米颗粒在平底筒仓中的流动形态基本是漏斗流。

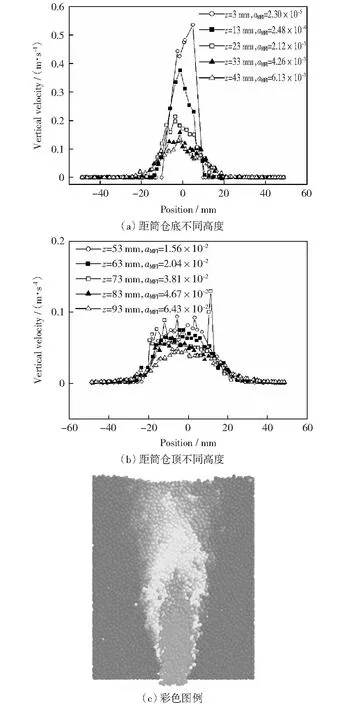
图7 玉米颗粒1 s时刻垂直速度分布图(自由运动)Fig.7 Vertical velocity profile at one second for corn (free flowing)

速度分布曲线剧烈波动位置，对应图7(c)中，颜色转变交界处。对于筒仓下部(高度大约43 mm处)靠近筒仓壁处的物料颗粒基本处于静止状态，因此速度曲线基本为水平线。而筒仓上部，靠近筒仓壁处的物料颗粒速度曲线呈现较短的水平线，表明物料颗粒正逐渐流入筒仓中心卸料区。

选取2 s时刻3个不同高度，分析螺旋辅助机运行下物料垂直速度(如图8所示)。由图可知，远离螺旋输送机的物料处，即离筒仓底部为3 mm处，垂直速度几乎不受螺旋运动的影响，与自由流动物料的速度分布几乎一致；即筒仓壁的附近物料颗粒几乎静止，中间卸料区物料颗粒运动速度成抛物线形，最高速度点为筒仓中心附近。距离筒仓底部13 mm处的速度变化规律也基本相似。但在高度23 mm处，由于受螺旋运动影响，与螺旋叶片接触的物料颗粒速度有明显波动，且速度值较高。速度幅度变化稳定部分，为卸料区漏斗型坡度处，叶片已经不与物料颗粒接触，只有物料的自由运动，因此螺旋运动没有改变物料的流动形态。

图8 玉米颗粒2 s时刻垂直速度分布图(螺旋运动)Fig.8 Vertical velocity profile at two second for corn(screw moving)

4 结论

本文使用EDEM软件仿真物料在筒仓中自由流动和螺旋辅助卸料情况下物料流动速度特性，得出如下结论：

1) 玉米颗粒在平底筒仓中自由流动形态是漏斗流。

2) 玉米颗粒自由流动时，在靠近筒仓壁处的颗粒运动速度与中间颗粒运动速度的变化趋势基本一致。当两边颗粒沿滑移面流向漏斗形卸料区域时，速度发生波动，而中间颗粒逐渐流向卸料口，进行自由落体运动，进入快速颗粒流动过程，进而加速流出卸料口，速度达到最大值。

3) 螺旋输送机会影响筒仓壁处颗粒的流动速度，而对于中间颗粒的运动速度趋势基本没有影响，距离螺旋机越近，物料颗粒速度波动越大。

[1] COUTO A,RUIZ A,AGUADO P J.Design and instrumentation of a mid-size test station for measuring static and dynamic pressures in silos under different conditions-part I:description[J].Computers and Electronics in Agriculture,2012,85:164-173.

[3] JACA R C,GODOY L A,FLORES F G,et al.A reduced stiffness approach for the buckling of open cylindrical tanks under wind loads[J].Thin-Walled Structures,2007,45(9):727-736.

[4] SONG C Y.Effects of patch loads on structural behavior of circular flat-bottomed steel silos[J].Thin-Walled Structures,2004,42(11):1519-1542.

[5] WILDE K,TEJCHMAN J,RUCKA M,et al.Experimental and theoretical investigations of silo music[J].Powder Technology,2010,198(1):38-48.

[6] WENSRICH C.Numerical modelling of quaking in tall silos[J].International Journal of Mechanical Sciences,2003,45(3):541-551.

[7] KOBYLKA R,MOLENDA M.DEM modelling of silo load asymmetry due to eccentric filling and discharge[J].Powder Technology,2013,233:65-71.

[9] CLEARY P W,SAWLEY M L.DEM modelling of industrial granular flows:3D case studies and the effect of particle shape on hopper discharge[J].Applied Mathematical Modelling,2002,26(2):89-111.

[10] KOBYLKA R,MOLENDA M.DEM modelling of silo load asymmetry due to eccentric filling and discharge[J].Powder Technology,2013,233:65-71.

[12] LANGSTON P A,AL-AWAMLEH M A,FRAIGE F Y,et al.Distinct element modelling of non-spherical frictionless particle flow[J].Chemical Engineering Science,2004,59(2):425-435.

[13] OLDAL I,KEPPLER I,CSIZMADIA B,et al.Outflow properties of silos:the effect of arching[J].Advanced Powder Technology,2012,23(3):290-297.

[15] SIELAMOWICZ I,CZECH M.Analysis of the radial flow assumption in a converging model silo[J].Biosystems Engineering,2010,106(4):412-422.

[17] YIN W,LU YONG,OOI J Y.Numerical modelling of dynamic pressure and flow in hopper discharge using the arbitrary lagrangian-eulerian formulation[J].Engineering Structures,2013,56(6):1308-1320.

[18] SIELAMOWICZ I,CZECH M,KOWALEWSKI T A,et al.Empirical description of granular flow inside a model silo with vertical walls[J].Biosystems Engineering,2011,108(4):334-344.

[19] YANG S,HSIAU S.The simulation and experimental study of granular materials discharged from a silo with the placement of inserts[J].Powder Technology,2001,120(3):244-255.

[20] OOSTERHUIS E,SCHOTT D,VAN WIJK A.The reclaim screw in mammoth silos operating on a free surface:comparison between horizontal and inclined operation on free flowing bulk solids[J].Part Syst Charact,2004,21(4):332-339.

[21] KETTERHAGEN W R,CURTIC J S,WASSGREN C R,et al.Predicting the flow mode from hoppers using the discrete element method[J].Powder Technology,2009,195(1):1-10.

[22] JOHANSON J R.Stress and velocity fields in the gravity flow of bulk solids[J].Journal of Appliect Mechanics,1964,31(3):499.

[23] NEDDERMAN R M.Statics and kinematics of granular materials[M].Cambrige:Cambridge University Press,1992.

[24] BALEVI IUS R,SIELAMOWICZ I,MRZ Z,et al.Effect of rolling friction on wall pressure,discharge velocity and outflow of granular material from a flat-bottomed bin[J].Particuology,2012,10(6):672-682.

[25] SIELAMOWICZ I,CZECH M,KOWALEWSKI T A,et al.Empirical description of granular flow inside a model silo with vertical walls[J].Bio Systems Engineering,2011,108(4):334-344.

[27] 周文秀.玉米籽粒的物理力学特性研究[D].哈尔滨:东北农业大学,2015.

[28] COETZEE C J,ELS D N J.Calibration of granular material parameters for DEM modelling and numerical verification by blade-granular material interaction[J].Journal of Terramechanics,2009,46(1):15-26.

[29] LI Y,XU Y,JIANG S.DEM simulations and experiments of pebble flow with monosized spheres[J].Powder Technology,2009,193(3):312-318.