一种新颖的模拟电路故障诊断方法

谢 涛， 李 珩

1 引言

自上世纪70年代开始，模拟电路故障诊断技术就已受到学术界的广泛关注，且在全球范围内获得一定探究成果[1-12].模拟电路故障诊断技术逐步形成相对系统的理论，使得其在网络理论当中的地位得以确立，发展成为网络综合以及网络分析理论后的第三大分支.模拟电路故障诊断技术正处于探究电路理论的前沿领域.

在对模拟电路诊断系统进行构建之前，对体现电路状态的故障信息特征进行有效以及快速提取，往往作为诊断以及测试工作的关键以及难点所在[13，14].一般来说，原始数据的获取，可结合需检测电路响应的波形曲线来实现，在对其进行采样操作之后加以映射，让其转换到样本空间之中，如位置、类型等模拟电路故障信息均可能被包括在上述数据之中；但对样本整体空间进行考察后，可认识到上述特征信息分布并不固定，就各类诊断故障的方法来说，往往不可以在故障模式分类时直接运用，需通过恰当的处理、转变，方可完成对电路故障特征的有效提取，针对故障模式开展相应的压缩变换工作，对原始样本集对应的特征信息进行提取，形成对应特征空间[14].一般而言，多以PCA特征，即主成分分析特征的提取运用为主.从一定程度上来看，该方法可实现对原始故障相应特征信息的保持，但若结合信息统计方面而言，该算法针对主成分，只进行了二阶统计量的考虑，其仅可对平稳高斯分布数据进行描述，而诸多非高斯分布的随机变量，它的高阶累积量还包含有很多信息[14]，如可结合高阶累积量的运用，来表示非高斯数据，可对信号独立分量进行抽取，而作为常规PCA而言，这一目的往往无法达成.此外，在对故障信号进行提取时，往往只涉及到电压信号的提取，有时对这种单一信号的提取，无法对电路故障特征进行最大限度的表示，故障诊断的正确率也无法得到保障.所以，为实现故障诊断正确率的提升，需通过对不同信息源的信息加以利用，并以此作为特征向量，来诊断电路故障.出于上述目的，论文在这一方面运用了信息融合技术，除了电压以外，同时以电流这一重要的模拟电路信息作为故障特征向量构造的一大信息源，对以故障信息偏度、峭度为基础的特征提取方式加以论述.

2 高阶累积量、峭度和偏度

近年来，高阶累积量技术获得了快速发展，在非线性、非高斯以及盲信号的处理方面，其重要性日益突出，也受到了更多人的关注.其优势相对较多，如可对信号耦合特性予以提取、或是对系统非线性特性进行检测，且针对高斯噪声其并不敏感，从理论上来看，噪声影响可以忽略不计，可让辨识以及分析精度得以提升.就模拟电路故障信号自身而言，其属于一种非线性信号，遭受环境等相关因素影响后，必然会导致噪声存在于故障信号之中.所以通过对这一方法的运用来处理模拟电路故障信号，这是一个极佳的选择.

2.1 高阶累积量

结合对特征函数的引入，可针对高阶累积量进行如下定义[14]，就单一随机变量而言，其定义为

其中 ψ（ω）＝lnφ（ω）

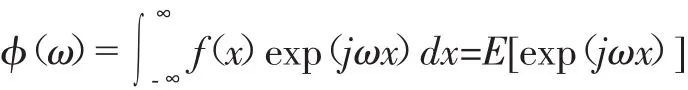
E{·}为求期望算子，代表统计平均.ψ（ω）、φ（ω）分别属于X这一随机变量的第一以及第二特征函数.就x=（x1，x2，…，xk）T这一随机矢量而言，高阶累积量定义具体如下：

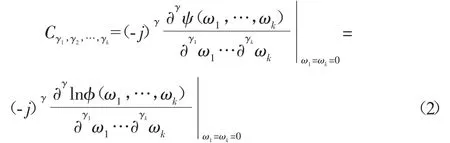
其中，φ（ω1，…，ωk）＝E[exp（j（ω1x1+…+ωkxk））]，γ=γ1+γ2+…γk.特别地，当取 γ1=γ2=γ3=1 及 γ=3 时，三阶累积量记为

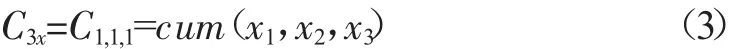
一般地，k阶累积量记为

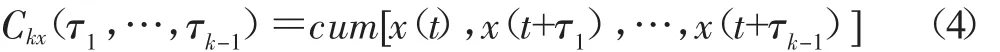
2.2 峭度和偏度

若{x（n）}为平稳随机过程且均值为零，则对应的一阶、二阶、三阶、四阶累积量如下：

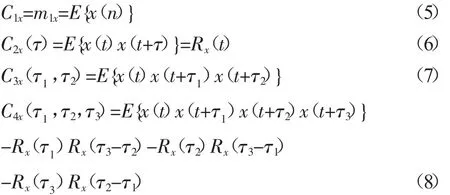
在（7）式中令 τ1=τ2=0，可获得三阶对应的 1-D 切片，即实信号{x（n）}的偏度（skewness）：Sx=E{x3（t）}；同样在（8）式中令 τ1=τ2=τ3=0，得到另一个重要的概念：峭度（kurtosis），记为：Kx=E{x4（t）}-3E2{x2（t）}.峭度常用作对随机变量或随机信号非高斯性的一个定量度量[15].

在此，Rx代表自相关.由上定义可得到：x这一高斯分布随机变量，其均值以及方差分别为一阶以及二阶累积量，其高阶累积量恒为零.若高斯随机过程x（n）阶次大于2，其对应的高阶累积量也是零.所以，高阶累积量对高斯过程并不敏感，若将高斯噪声外加于信号时，从理论上来看，高阶累积量可对噪声影响予以完全抑制，由此可实现识别、分析等精度的提升.

3 信息融合技术

上世纪70年代开始，信息融合这一概念被提出，在二十多年的发展历程当中，人们对这一技术更为关注[16-18].综合来看，信息融合活动，即属于处理多源信息的进程，结合信息计算动态进程，让信息量持续增加，转变无序信息为有序[14].本文集合对这一技术的运用，来识别以及诊断模拟电路的运行状态，其参考的思想如下：即电路运行状态，以及故障征兆之间，有一定的因果关系存在，但往往结合显式无法对上述复杂关系加以表达，因为自身特性，神经网络在识别电路运行这一不确定模式时，其具有特殊之处.结合信息融合抽象层次来进行划分，信息融合有决策层、特征层以及数据层融合.本文用到的方法是特征层融合方法[19].

4 基于峭度、偏度和信息融合技术模拟电路故障诊断原理

图1具体展示了诊断原理图.首先需将激励添加于待测电路之中，论文选用的是正弦激励信号，随后，在终端采样电流以及电压信号，通过高阶谱分析工具箱，求出其对应的skewness以及kurtosis值作为故障诊断的特征向量，再以此作为神经网络的输入，由神经网络来完成故障诊断.

5 诊断实例

图2展示的是四运放高通滤波器，R1=R4=5 kΩ，R2=R3=R5=R8=R9=R10=10 kΩ，R6=3 kΩ，R7=4 kΩ，C1=20 nF，C2=5 nF，激励为幅值6 V的交流电压.

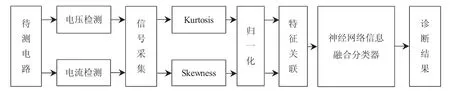
图1 故障诊断原理框图

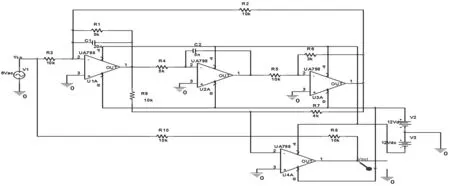
图2 四运放高通滤波器

对电路进行灵敏度分析后发现，针对电容C1﹑C2以及 R1﹑R4﹑R6﹑R7电阻而言，电路输出 Vout具有较大灵敏度.因此在 5%的元件容差范围内，对 R1﹑R4﹑R6﹑R7﹑C1﹑C2各正、负偏50%的电路软故障加以考虑，若包括无故障在内，则共有状态十三种.

在选取故障分类器时，对单隐层三层BP神经网络加以选用，以故障特征向量元素数量作为输入层.此处对故障特征向量的构造，选取输出电流以及电压的峭度和偏度，因此在输入层共有四个神经元，而在输出层，以故障状态数作为神经元数量，共有十三个，可针对输出向量进行如下定义：即假定电路状态为M种，则网络输出具体如下：（a1，a2，….ai….aj….aM）.如果此时电路为 i状态，则可令 ai=1，剩余均为零，也就是（0，0，….1，….0）为期望的网络输出向量；可结合经验公式[20]来求取隐层神经元数量.

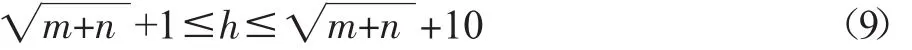
在此公式之中，输入以及输出的神经元数量分别为m以及n.

以5%为元件值容差范围，在0.5 kHz到1.5 MHz的频率范围内对电路所有状态开展100次Monte-Carlo分析，样本总数1 300个，其中训练样本为780个，测试样本则为520个.在不同电路状态时，表1对求取的电压和电流的偏度以及峭度进行了说明.神经网络诊断具体输出结果可参见表2.

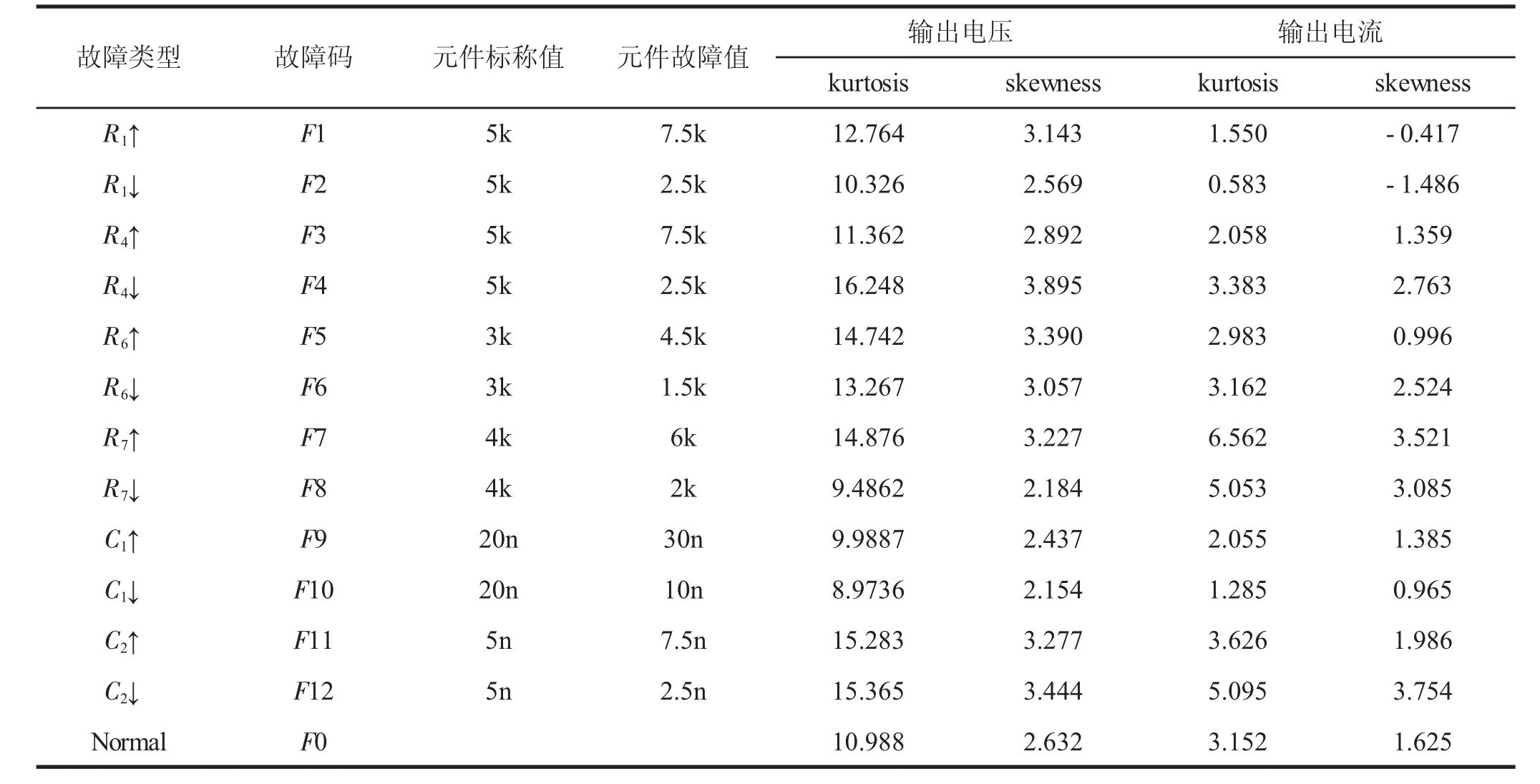
表1 电压、电流信号的kurtosis和skewness

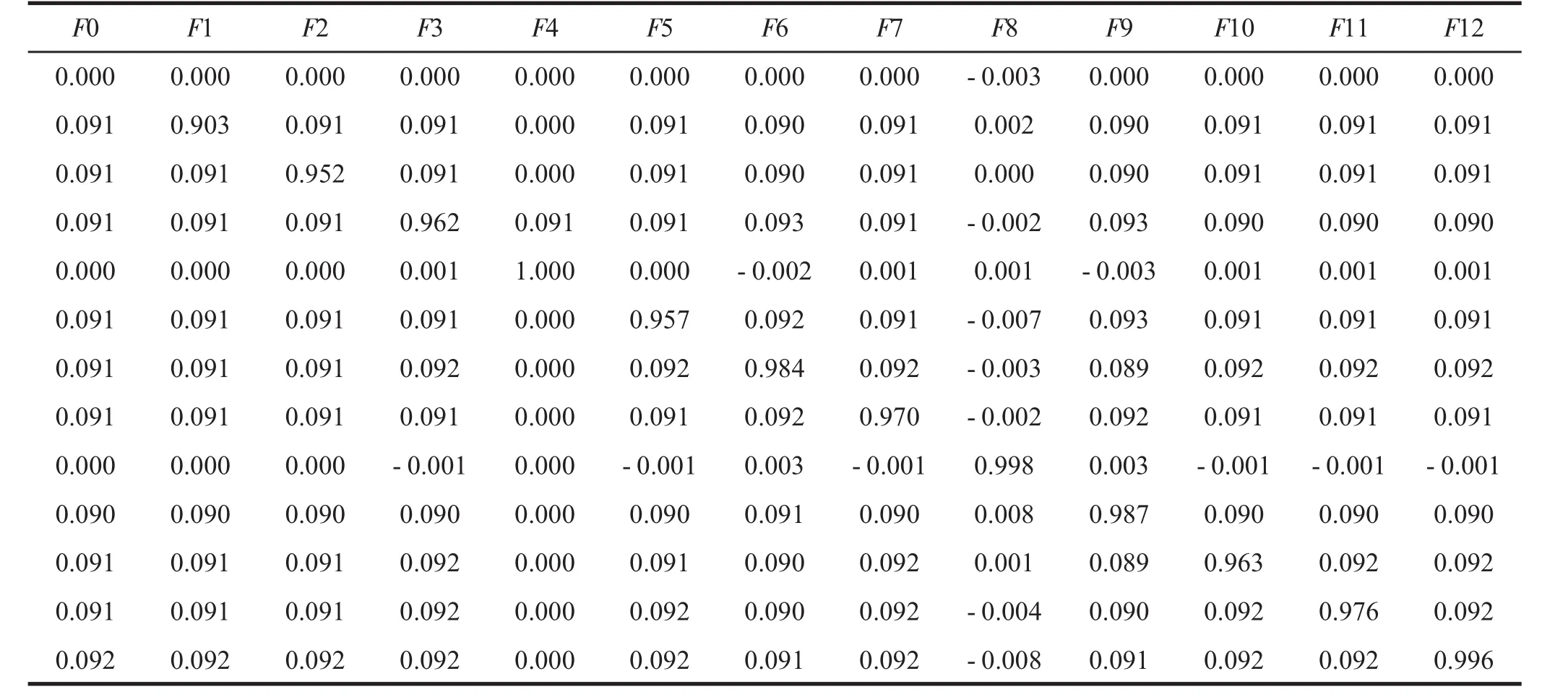
表2 神经网络诊断输出结果

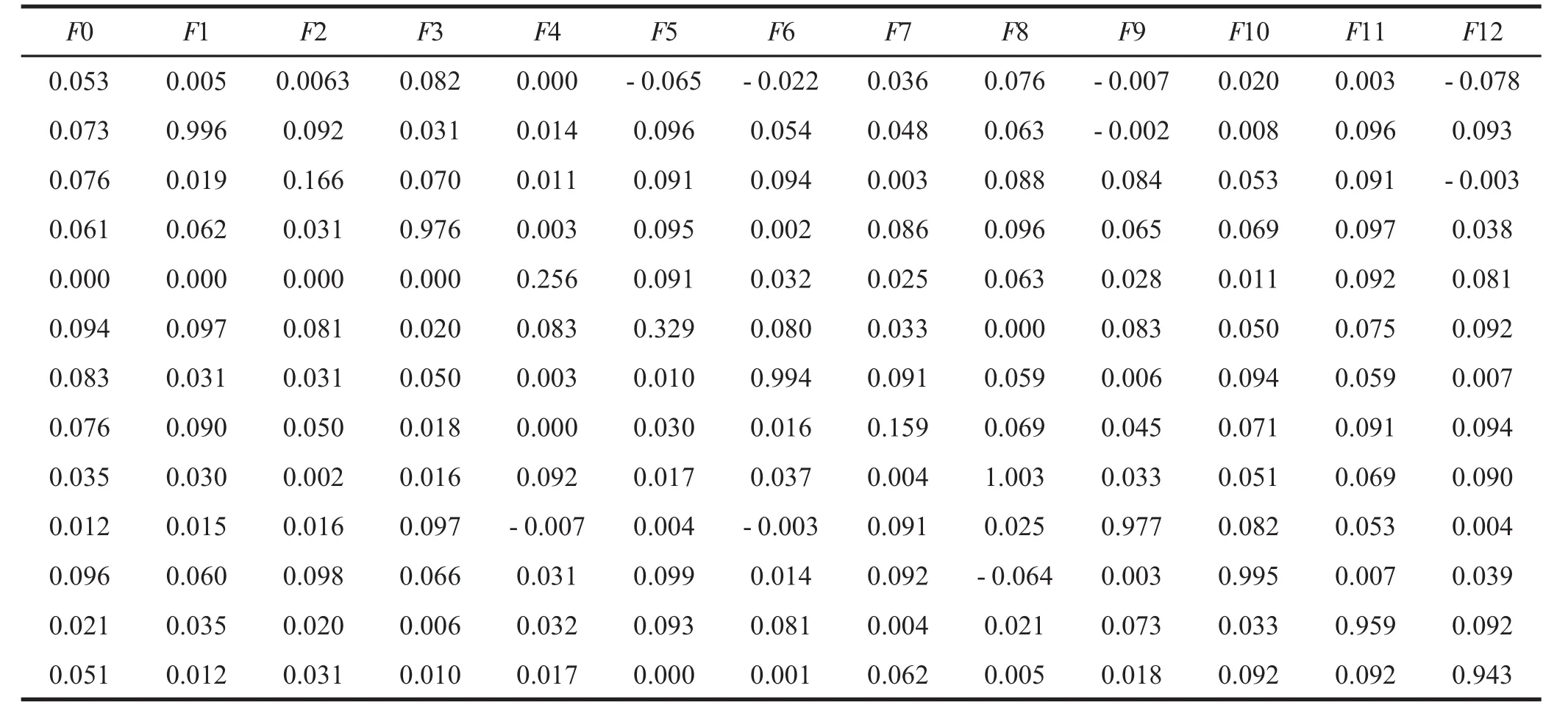
表3 小波神经网络诊断输出结果

kurtosis对各元器件的变化规律与skewness变化规律一致.

若用小波神经网络加输出电压信号的方式来进行诊断，不改变故障模式，在神经网络中输入电路输出电压的小波分解系数完成故障识别工作，表3具体展示了对应的诊断输出结果以及神经网络收敛曲线.

结合表1可以发现，在不同故障情况之下对应的输出电流以及电压，其skewness以及kutorsis数值差异相对较大，所以就上述四个数值构成的特征向量，具有较大的区分度，可更好的识别以及诊断故障.而结合表2的相应数据可以发现，其在诊断故障方面，准确率达到了百分之百.若在选定故障特征向量时，以输出电压信号小波分解系数作为向量，则对比论文提出方法而言，其准确率相对较差，结合表3可以看出，神经网络无法针对F2、F4、F5以及F7进行正确识别，分别和R1负偏，R4负偏，R6正偏和R7正偏4种故障相对应.

6 结论

本文从信号的峭度、偏度和信息融合技术多方面切入，对一种全新模拟电路故障诊断方法进行了论述：以输出电流以及电压信号的偏度、峭度为依据，完成故障特征向量的构造，打破了传统的二阶统计量刻画信号时要求信号高斯性、线性和平稳性等的局限；为了使得特征向量包含更多的故障信息，将电流信号这一极为关键的电路参量引入其中也作为故障特征，来完成故障特征向量的构造.诊断实例验证了该方法的可行性和高效性.

[1]He YG，Tan YH，Sun YC.Wavelet neural network approach for fault diagnosisof analog Circuits.IEEProc[J].Circuits Devices and Systems，2004，151（4）：379-384.

[2]谭阳红.基于小波和神经网络的大规模模拟电路故障诊断研究[D].长沙：湖南大学，2005.

[3]Tan YH，He YG Wu J.Neural network method of fault diagnosis for large-scale analogue circuits.Chinese Journal of electronics[J].2003，12（1）：57-60.

[4]谭阳红，何怡刚.模拟电路故障诊断的集团方法[J].电子测量与仪器学报，2003，17（4）：57-62.

[6]Yang CL，Tian SL，Long B，et al.Methods of Handling the Tolerance and Test-Point Selection Problem for Analog-Circuit Faulat Diagnosis[J].IEEE Trans.On Instrmmentation and Measurement，2011，60（1）：176-185.

[7]Wey CL，Krishman S.Bulit-in self-test （BIST）structure for analogcircuit fault diagnosiswith current test data[J].IEEETrans.On Instrumentation and Measurement，1992，41（4）：535-539.

[8]Slamani M，Kaminska B.Analog circuit fault diagnosis based on sensitivity computation an functional testing[J].Design&Test of Computers，IEEE，1992，9（1）：30-39.

[9]Robotycki A，Zielonko R.Fault diagnosis of analog piecewise linear circuits based on homotopy [J].IEEE Trans.On Instrumentation and Measurement，2002，51（4）：876-881.

[10]Aminian F，Aminian M，Collins H W.Analog fault diagnosis of actual circuits using neural networks[J].IEEE Trans.On Instrumentation and Measurement，2002，51（3）：544-550.

[11]Worsman M，Wong M W T，Lee Y S.Enhancing the fault diagnosis of linear analog circiuit steady-state DC testing through the analysis of equivalent faults[J].IEEE Trans.On Circuits and systemⅠ：Fundamental Theory and Applications，2003，50（7）：932-936.

[12]Yuan LF，He YG，Huang JY，et al.A New Neural-Network-Based Fault Diagnosis Approach for Analog Circuits by Using Kurtosis and Entropy as a Preprocessor[J].IEEE Trans.On Instrumentation and Measurement，2010，59（3）：586-595.

[13]虞和济，陈长征.基于神经网络的智能诊断[M].北京：冶金工业出版社，2000：9-32.

[14]谢涛.基于（多）小波（包）神经网络及优化的模拟电路故障诊断研究[D].长沙：湖南大学，2011.

[15]Aapo H，Juha K，Erkki O.Independent Component Analysis[M].周宗潭，董国华，徐昕，等译.北京：电子工业出版社，2007：15-30.

[16]Sun SL.Optimal and self-tuning information fusion Kalman multi-step predictor[J].Aerospace and Electronic Systems，2007，43（2）：418-427.

[17]Shivappa ST，Trivedi MM，Rao BD.Audiovisual Information Fusion in Human Computer Interfaces and Intelligent Environments[J].A Survey Proceedings of the IEEE，2010，98（10）：1692-1715.

[18]Zhang YM，Ji Q.Efficient Sensor Selection for Active Information Fusion[J].Systems，Man，and Cybernetics，Part B：Cybernetics，2010，40（3）：719-728.

[19]王承，孙秀斌，谢永乐.基于神经网络信息融合技术的模拟电路故障诊断[J].电路与系统学报，2007，12（5）：25-29.

[20]Deliyannis T，Sun Y，Fidler JK.Continuous-Time Active Filter Design Boca Raton[M].FL：CRCPress，1999：20-23.