ZnGeP2晶体力学性质的第一性原理研究
2018-01-19张顺如谢林华
张顺如, 谢林华
1 引言
磷锗锌(ZnGeP2)晶体是性能优异的中远红外高功率激光频率转换新材料,可实现红外激光倍频、二次谐波产生和光参量振荡、在红外跟踪、红外制导、激光雷达和激光医学等军事和民用领域具有广泛而重要的应用前景[1].近年来,美国和俄罗斯科学家对磷锗锌单晶体的生长技术进行了深入的研究,已经可以生长出高质量的ZnGeP2单晶体[2,3],国内四川大学朱世富课题组,哈工大杨春辉课题组,中科院安徽光机所吴海信课题组,四川省新材料中心康彬等人,山东大学顾庆天等人也相继开始进行了ZnGeP2晶体材料的生长及应用研究[4-8].然而,对这种晶体的理论研究报道还不多,有些实验现象的解释还不能令人满意、机理尚不够清楚.因此,继续深入从理论上研究它们的物理性质及其机理,对于高性能磷锗锌的多晶合成、单晶体生长及其应用,具有重要的理论意义和实用价值.
本文采用密度泛函理论的第一性原理方法,对非线性光学材料磷锗锌的几何结构、弹性常数进行了计算,发现沿晶体a轴和c轴方向的弹性常数是其它晶向的2倍左右,利用计算所得到的ZnGeP2晶体的弹性常数,采用Voigt-Reuss-Hill近似得到了黄铜矿结构的ZnGeP2晶体的力学性质,可为ZnGeP2晶体的机械加工提供参考.
2 计算方法
我们系统地计算了ZnGeP2晶体的结构参量和弹性常数.所有的计算都基于平面波赝势的密度泛函理论,软件为CASTEP[9,10].计算中采用Vanderbilt超软赝势(ultrasoft pseudopotentials)[11]描述电子与离子实之间的相互作用.Zn的3 d,4 s电子,Ge的4 s,4 p电子,以及P的3 s,3 p电子均视为价电子.交换关联能采用基于广义梯度近似Perdew Burke Ernzerhof(PBE-GGA)泛函[12].在结构优化时,采取平面波的截断能为600 eV,设置所有原子位置充分优化到每个离子上的力小于0.01 eV/Å,每个离子上的应力小于0.02 GPa,相继两次结构参数变化引起的原子位移的分量小于1.0x10-4Å,相继两次自洽计算得到的晶体总能量之差小于1.0x10-6eV/atom,以确保计算时能量是高度收敛的.计算中选取K点为8×8×8的Monkhorst-Pack网格.
用应力应变方法来得到弹性常数.在计算得到的弹性常数Cij的基础上,用Voigt-Reuss-Hill近似进一步估算出ZnGeP2晶体的体弹性模量B、剪切模量G、杨氏模量Y和泊松比ν.
3 结果及讨论
3.1 晶体结构
ZnGeP2晶体属于II-IV-V2型黄铜矿结构的化合物半导体,与目前广泛研究的III-V结构半导体GaP和GaAs是同构异分体.这类三元黄铜矿结构可以看作是从III-V型二元化合物通过有规律的交替用IIB族和IVB的金属阳离子替代沿C轴的IIIB族阳离子而得到.晶胞内的每个阳离子都被四个阴离子以四面体形式环绕包围,但是与理想的正四面体顶点位置有一个小距离的变形u,该变形量u可以表示成晶格参量的函数:
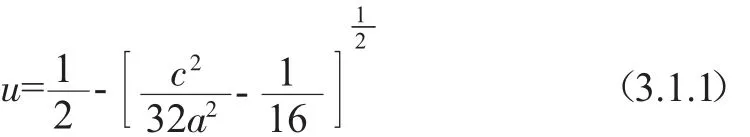
通常,II-V离子和IV-V离子之间的键长是不相等的,分别用dII-V和dIV-V表示.这两种不同的阳离子和阴离子之间的键长可由公式表示为:
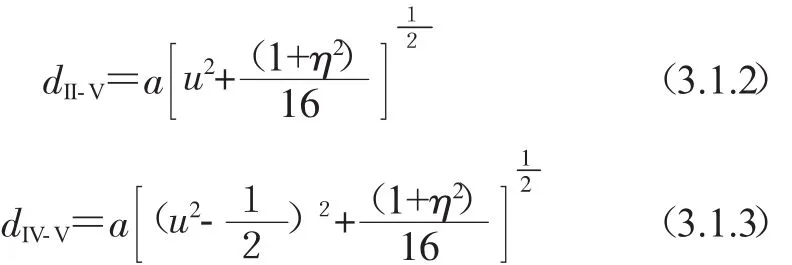
我们计算了ZnGeP2晶体在平衡结构附近总能量随体积变化的曲线(图1),计算出的曲线采用Birch-Murnaghan状态方程[13]拟合:
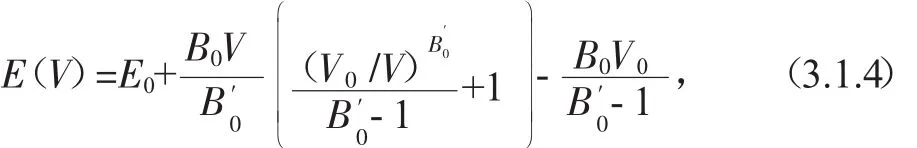
其中,E0为平衡结构时的能量,B0为体弹模量为体弹模量B0对压强P的一阶导数.拟合可以得到ZnGeP2晶体的平衡结构体积、体弹性模量、体弹性模量对压强的一阶导数.为了方便与文献[14-17]报道过的实验值相比较,计算出来的结构参量 a,c,u 和键长 d(Zn,p),d(Ge,p),体弹性模量B0以及体弹性模量对压强的一阶导数B′0都列在表1.从表1可以看出,计算出的ZnGeP2晶体平衡晶格常数a为5.480Å,c为10.791Å,与实验值相比较,分别偏离0.27-0.36%,0.75-0.84%,这种偏离程度是处于第一性原理允许的误差范围以内的,同时发现拟合得到的体弹性模量B0及体弹性模量对压强的一阶导数B′0跟实验值的差异较小.
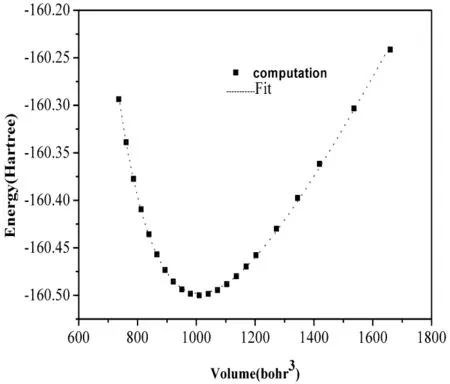
图1 ZnGeP2晶体体积-总能量变化曲线

表1 ZnGeP2的晶格参数a(Å),c(Å),内禀参数u,键长Zn-P(Å)和Ge-P(Å),体弹模量B(0GPa)和体弹模量对压强的一阶导数B′0
3.2 弹性常数
胡克定律表明,对于足够小的形变,应力与应变成正比,因此应力分量是应变分量的线性函数,可以把这个关系写成矩阵形式的表示式[18]:

式中Cij称为弹性常数,表征材料弹性的量.可以证明Cij=Cji,所以弹性常数张量最多只有21个独立的常数.随着晶系的对称性增高,独立张量元的数目减少.不同晶系的独立弹性常数数目不同,据我们所知,由于ZnGeP2晶体属于空间群,具有四方对称性,其弹性常数张量具有六个独立张量,根据杨氏的定义,分别为C11,C33,C44,C66,C12和 C13.
目前为止,尚没有关于ZnGeP2晶体弹性常数实验值的报道,学者们前后分别采用壳层模型[19],硬离子模型[20]来估计ZnGeP2晶体的弹性常数:由于模型较为简单,计算所得到的ZnGeP2的弹性常数存在疑点.
本文采用密度函数理论计算结合线弹性理论,可以较准确地计算出ZnGeP2单晶体材料的弹性常数,见表2. 可以发现,C11,C33是 C44,C66,C12和 C13的 2 倍左右,即沿晶体a轴和c轴方向的弹性常数是其他晶向的2倍左右.我们计算得到的弹性常数及其组合满足波恩力学稳定性标准[21],该标准要求四角对称的ZnGeP2晶体的弹性 常 数 满 足 :C11,C33,C44,C66>0,C11>C12,C11C33>C213,.这说明我们计算所得到的ZnGeP2的固体结构是机械稳定的,反证了我们计算的弹性常数是合理的.

表2 ZnGeP2晶体的弹性常数Cij(GPa)

表3 ZnGeP2晶体的体弹模量B H(GPa),剪切模量G H(GPa)、线性和体压缩率χa,χc,χ(TPa-1)以及弹性各向异性因子a1,α2
3.3 力学性质
由ZnGeP2单晶体的各向异性弹性张量组合可得到ZnGeP2晶体聚合物的各向同性体弹性模量.由于Voigt[22]和Reuss[23]近似所进行的各向同性平均所得到的体弹性模量和剪切模量分别代表理论上限值和下限值,Hill[17]认为多晶聚合物的真实(或可靠)体弹模量和剪切模量应该取Voigt和Reuss近似两种近似结果的算术平均,即:

其中BV是Voigt体弹模量,BR是Reuss体弹模量,GV是Voigt剪切模量,GR是Reuss剪切模量.此种方法估计的体弹性模量跟实验值非常接近,而用其他文献[19,20]报道的弹性常数数据通过Hill近似得到的结果并不如此.利用BH和GH,我们可以获得ZnGeP2单晶体的杨氏模量:

泊松比:
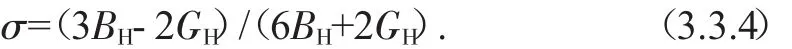
此外,根据已知的弹性常数Cij,我们很容易可以得出晶体沿a和c轴的线性压缩率χa,χc,以及体积压缩率χ[24],这些结果都集中在表3.
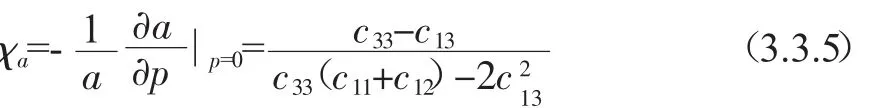
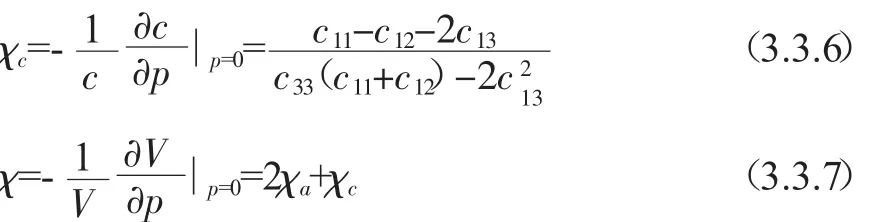
结果显示,沿晶体a和c轴方向的两个线性压缩率χa和 χc之间的差别很小,即比值 χa/χc≈1.而体积压缩率和其他两个文献得到的理论值非常接近[19,20].但是,利用这些弹性常数Cij,两个弹性各向异性因子分别为a1=2C11/(C11-C12)=1.7958,a2=C66/C44=0.9816,巨大的差异表明黄铜矿ZnGeP2单晶体强大的弹性各向异性;而且本工作得到的各向异性因子跟文献得到的理论值[19,20]相比有明显的差异,我们给出的弹性各向异性结果没有文献中的大,我们的结果表明ZnGeP2晶体在三个轴方向上更趋向于弹性各向同性,而这恰恰跟实验结论[20]更符合.
4 结论
本文用第一性原理的方法系统研究了黄铜矿结构的ZnGeP2晶体的结构性质,弹性性质.计算了ZnGeP2晶体的基态时的平衡结构参数,如晶格常数,内禀参量以及 d(Zn,P),d(Ge,P)的键长,计算出的结果与已有的实验值、理论值相符合.计算了ZnGeP2的弹性常数,研究发现沿晶体a轴和c轴方向的弹性常数是其它晶向的2倍左右,对比分析了以往两种方法所计算的ZnGeP2晶体的弹性常数的不足,证实我们计算的弹性常数比文献报道的理论值更可靠.根据我们计算所得到的ZnGeP2晶体的弹性常数,采用Voigt-Reuss-Hill近似计算了黄铜矿结构的ZnGeP2晶体的各向同性体弹性模量B,各向同性杨氏模量Y,各向同性剪切模量G,各向异性因子A,泊松比v.
[1]赵欣,朱世富,李梦.磷锗锌生长技术进展[J].半导体技术,2016,41(4):241-260.
[2]G.A.Velozubova,A.Y.Trofimov,et al.Melt nonstoichiometry and defect structure of ZnGeP2crystals[J].Crystallogr.Rep,2010,55:65-70.
[3]E.Buehler,J.H.Wernick,J.D.Wiley.The ZnP2-Ge system and growth of single crystals of ZnGeP2[J].Journal of Electronic Materials,1973(2):445-453.
[4]杨春晖,王猛,夏士兴,等.ZnGeP2晶体的合成与生长[J].人工晶体学报,2009,38(3):812.
[5]赵欣,朱世富,赵北君,等.ZnGeP2的多晶合成与单晶生长研究[J].无机化学学报,2009,25(1):99-103.
[6]林彦霆,顾庆天,刘宏,等.ZnGeP2多晶料合成与晶体生长[J].功能材料,2006,37(6):864-866.
[7]吴海信,倪友保,耿磊,等.红外非线性晶体ZnGeP2的生长及品质研究[J].人工晶体学报,2007,36(3):507-511.
[8]康彬,窦云巍,唐明静,袁泽锐,等.水平梯度冷凝法生长优质ZnGeP2单晶及性能表征[J].硅酸盐学报,2016,44:503-507.
[9]M.C.Payne,M.P.Teter,D.C.Allen,etal.Iterativeminimization techniques for ab initio total-energy calculations:molecular dynamics and conjugategradients[J].Rev.Mod.Phys.1992,64:1045-1097.
[10]V.Milman,B.Winkler,J.A.White,et al.Electronic structure,properties,and phase stability of inorganic crystals:A pseudopotential plane-wavestudy[J].Int.J.Quantum Chem,2000,77:895.
[11]D.Vanderbilt.Soft self-consistent pseudopotentialsin ageneralized eigenvalueformalism[J].Phys.Rev.B,1990,41:7892-7895.
[12]J.P.Perdew,K.Burke,and M.Ernzerhof.Generalized Gradient Approximation Made Simple[J].Phys.Rev.Lett,1996,77:3865-3868.
[13]F.Birch.Finite Elastic Strain of Cubic Crystals[J].Phys.Rev,1947,71:809-824.
[14]A.A.Vaipolin Inherent structural defects in AIIBIVC2Vcompounds[J].Fiz.Tverd.Tela,1973,15:1430.
[15]M.D.Lind and R.W.Grant.Structural dependence of birefringence in the chalcopyrite structure.Refinement of the structural parameters of ZnGeP2and ZnSiAs2[J].J.Chem.Phys,.1973,58:357-362.
[16]J.L.Shay and J.H.Wernick.Ternary Chalcopyrite Semiconductors:Growth,Electronic Properties,and Applications[M].New York:A.Wheaton Pergamon Press,1975.
[17]R.Hill.The Elastic Behaviour of a Crystalline Aggregate[J].Proc.Soc.Lond.A,1952,65:349.
[18]方俊鑫,陆栋.固体物理学[M].上海:上海科学技术出版社,1980.
[19]P.Zapol and R.Pandey.Atomistic calculations of defects in ZnGeP2[J].J.Appl.Phys,1996,79:671-675.
[20]A.S.Poplavnoi.Lattice-dynamics and chemical bond in semiconductor compound-II,compound-IV,compound-V2[J].Izv.Vyssh.Uchebn.Zaved.Fiz,1986(8):5.
[21]Born M and Huang K.Dynamical Theory of Crystal Lattices[M].Oxford:Clarendon,1954.
[22]W.Voigt.Lehrbuch der Kristallphysik[M].Teubner,1928.
[23]A.Recussand Z.Angew,Math.Mech,1929(9):49.
[24]Neumann H.Latticedynamicsand related propertiesof AIBIIIand AIIBIVcompounds,I.Elastic constants[J].Cryst.Res.Technol,2004,39:939-958.
