人体神经系统中的电势差和电流

李晨曦 刘玉颖 吕洪凤

(中国农业大学 1工学院， 2理学院，北京 100083)

电学是物理学研究领域中的一个重要分支。电不仅仅只存在于雷电、摩擦起电等无生命的物质中，自1780年意大利科学家伽伐尼在解剖青蛙时偶然发现电对肌肉的作用以来，人们逐渐认识到，在生物体内存在微弱电流，并发生着电势差的变化[1]。

生物有机体中电现象最显著的应用是动物体内神经系统中的电流。体内的特殊细胞——神经元交互链接形成的复杂网络可以接收、处理和传导电信号。该网络的中心位于大脑，储存并分析信息。神经系统根据这些信息控制机体的其他部位。神经系统非常复杂，人体内的神经系统包含1010个互相联系的神经元。信息通过神经元以电信号的方式传导，当神经元接收到外部刺激时，它将产生一个电信号脉冲并且沿着其细胞结构进行传输，不同数目的电信号脉冲则可以用来表现不同的信号强度，当信号传输到神经元细胞的末端时，继续激发其他神经元或肌肉细胞[2]。

本文以人体神经系统为例，详细介绍神经系统中神经细胞电势差及其神经脉冲信号传递的基本物理原理。

1 神经系统结构和功能简介

人体神经系统中充满了电荷流动的现象，这种生物电为我们感知外界世界提供可能；电信号在神经系统的神经元上传导。

神经元是一种具有特殊形状的活细胞，如图1所示，连接在主胞体上的是一些叫做树突的附属物和一根长长的轴突。信号被树突接收后沿着轴突进行传导，当一个信号到达神经末梢时，信号被传递给下一个神经元或突触连接处的肌肉。部分神经元有许多分离细胞(许旺细胞)包绕轴突，它们形成了一个被称为髓鞘的分层鞘来隔离彼此。

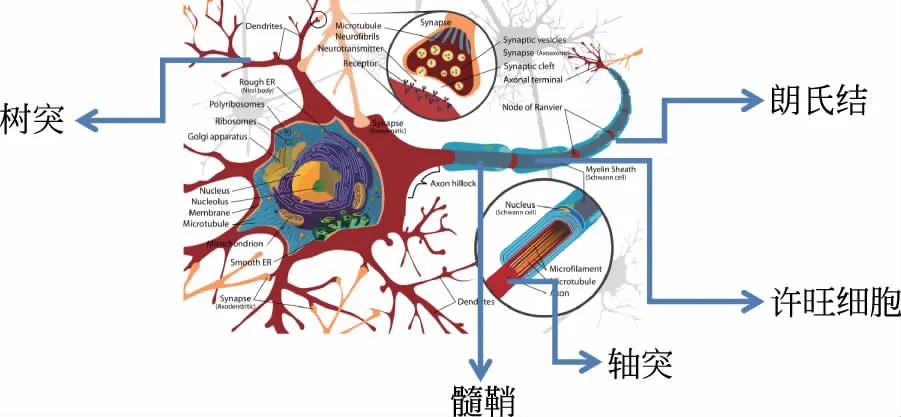
图1 神经元的基本结构示意图[3]

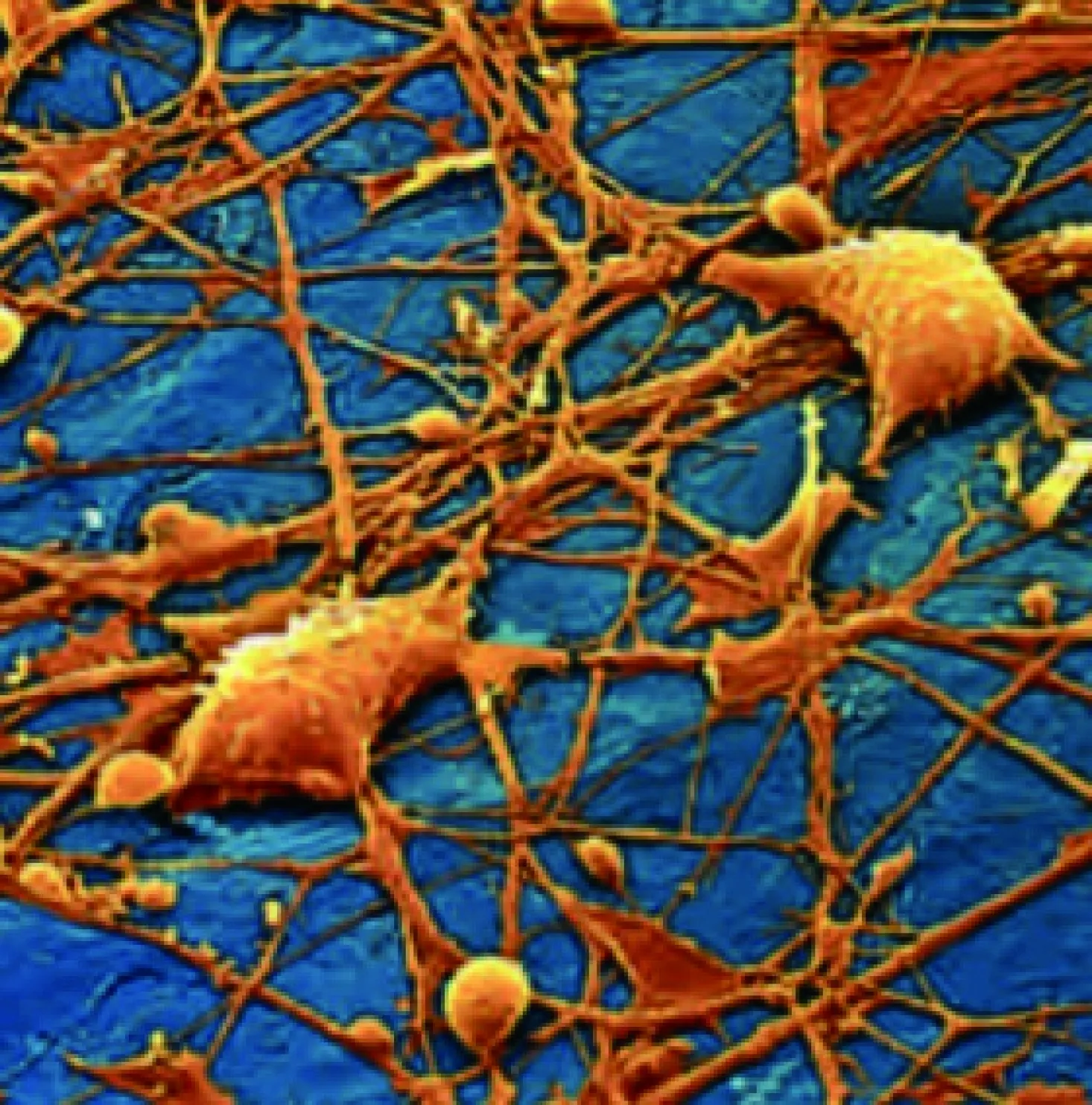
图2 人体内神经元网络[4]

神经系统的3大主要功能：第一，神经元能够传导来自感受器官或其他器官的信息并传递到由大脑和脊柱组成的神经中枢；第二，神经元加工来自神经中枢的信息并传递至肌肉或其他器官；第三，神经元可以在神经中枢内部进行信息加工和传递。大量的神经细胞纵横交错连接使这个系统精密而神奇(如图2所示)。神经传导是神经元传递电信号的一个基本术语，它是生物电的一个重要分支[4]。

2 神经细胞产生的电势差——静息电位与动作电位

2.1 静息电位

每一个神经元都由连接输入端的树突、胞体和将信息从细胞内传输出去的轴突相连而成，一个简单的感觉神经元电路如图3所示，从肌肉产生的神经冲动传输至脊柱，在这里信号被传输到运动神经元，反过来传输冲动来控制肌肉。

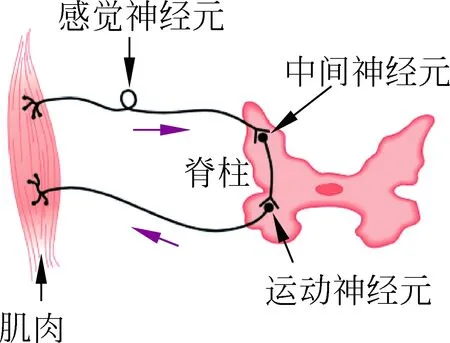
图3 感觉神经元电路[4]

如图4所示，在轴突中插入细针状的探针可以检测到流入轴突的电流，因为轴突的直径都非常小，即使是人体神经系统中最大的轴突其直径只有20μm，该实验难度较大。幸运的是大王乌贼神经轴突直径为0.5mm，足以容纳探针的插入，所以大部分神经系统信号传输的信息来自大王乌贼神经的实验[2]。

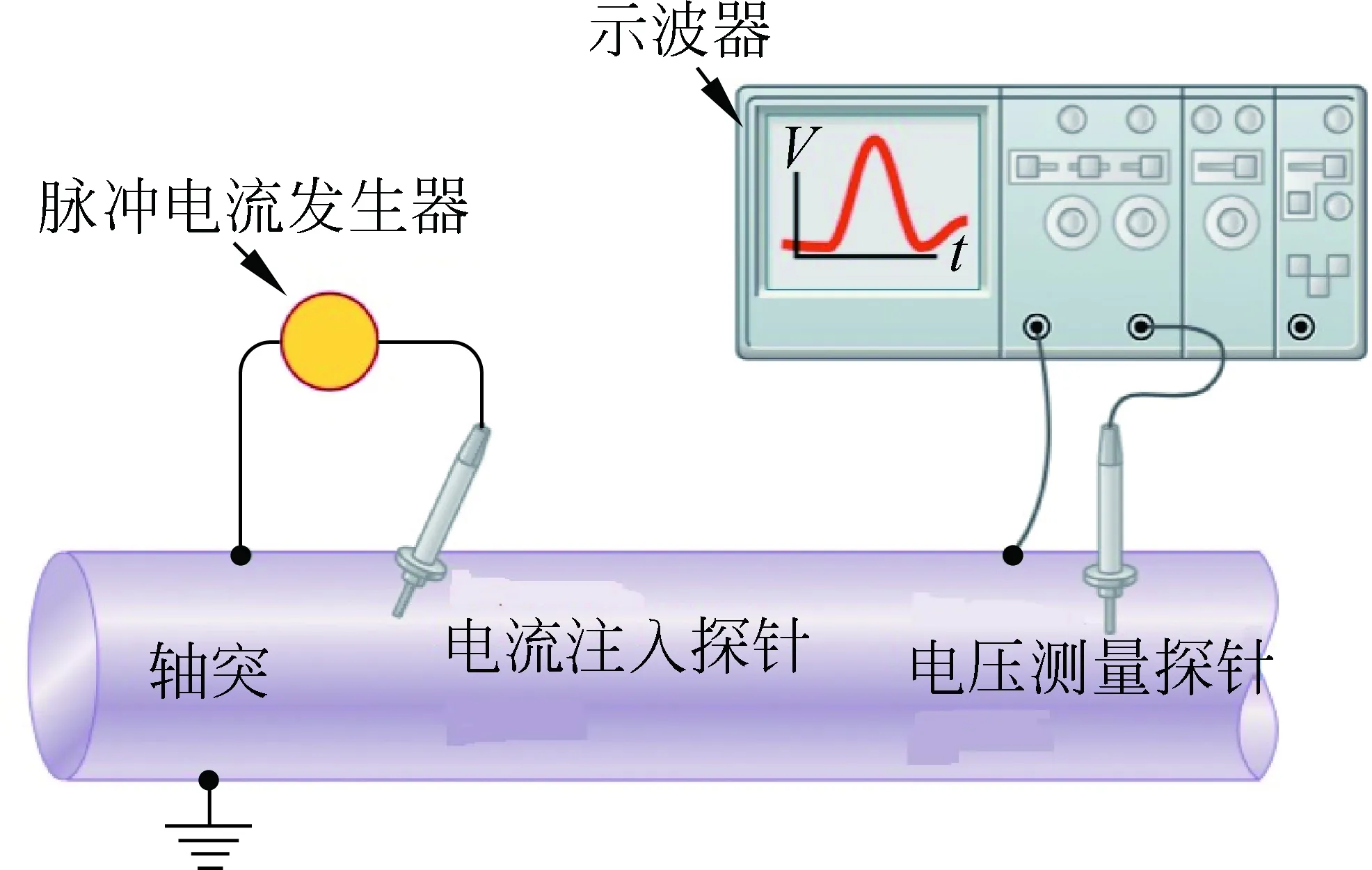
图4 将探针插入轴突内部测量电信号[4]示意图

在静息状态下，轴突不传导电脉冲，薄薄的轴突细胞膜两侧具有不同浓度的离子，其中最主要的是钠离子、钾离子和氯离子。细胞膜具有选择透过性，也就是说，部分离子可以透过细胞膜而其他离子不能。在静息状态下细胞膜阻碍钠离子流入细胞(甚至通过主动运输的方式将钠离子泵出细胞外)，但是它允许氯离子和少量钾离子的流入。因为细胞内部的钾离子浓度高于外部浓度，相比于扩散至细胞内，更多的钾离子趋向于扩散至细胞外；钾离子穿过细胞膜后附着在细胞膜外表面上，并留下等量的负电荷附着在细胞膜的内表面上，由于异号电荷相互吸引，离子在细胞膜上稳定存在。由于细胞外氯离子浓度较高易于扩散至细胞内，钾离子和氯离子的扩散行为都趋向于使细胞内膜呈负电性而外膜呈正电性。钾离子和氯离子的扩散会在细胞膜内外各产生一层正电荷和负电荷。然而，库仑力会阻碍离子继续扩散，随着电荷在细胞膜表面的积累，离子变得更难穿越细胞膜。当细胞膜两侧的离子浓度差和电势差正好达到平衡时，细胞就达到平衡状态。在扩散力和库仑力的平衡下，细胞膜两侧形成稳定的电荷层[5]。

细胞膜内与膜外之间存在着一定的电势差，称为跨膜电势差，也称为膜电位。膜电位是由于细胞膜内、外液中离子浓度不同及细胞膜对不同种类的离子通透性不同而引起的。细胞膜内外存在70～90mV的电势差，使仅有5～10nm厚的轴突细胞膜拥有大约106V/m的强电场，从而对其结构和渗透性产生了根本性影响。若神经元外侧电势为零，则内侧的静息电位大概为-90mV。当一个神经元不传导信号时，这个“静息电位”通常被表达为：V内-V外，数值一般从-60mV到-90mV，该电势差在任何一个动物细胞内都存在，在肌肉细胞和神经细胞内电势差最大。事实上，细胞消耗的所有能量的25%用来创造和保持该电势差[5]。

综上，跨膜电势差的形成是电场力和化学扩散力的一种相对平衡，于是我们用“能斯特(Nernst)方程”来定量描述。能斯特方程是定量描述离子在A、B两体系间扩散形成电势差的方程。 能斯特方程是关于分子热运动和电场力平衡时所需的电压。因此，温度越高，分子热运动的势能越大，膜两边浓度差越大，则所需的平衡电位越高[6]。由于在静息状态下，细胞膜对其他离子的通透性很小，但对钾离子通道处于开放状态，而静息电位也是由于钾离子顺浓度梯度扩散与阻碍钾离子扩散的电场力相互平衡得到的结果，所以静息电位就是钾离子的平衡电势差。由表1提供的数据，我们可以通过能斯特方程计算出细胞跨膜静息电位的大小，具体过程如下：

以轴突细胞为例，处于静息状态下细胞内外的离子浓度如表1所示。

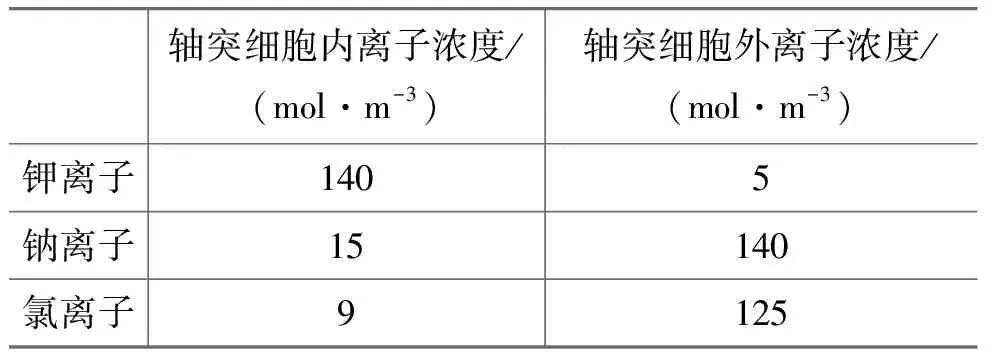
表1 轴突细胞内外的离子浓度

能斯特方程标准形式为

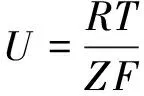
(1)

其中，ΔU为膜两侧的电势差；R是理想气体常数(8.31J/(K·mol-1))；T是热力学温度(可将体温视为37℃，换算得310.15K);Z是化合价，钾、钠、氯离子的Z分别为+1和-1;F是法拉第常数(96.487kJ·(V-1·mol-1))；[I]o和[I]i分别表示膜外和膜内的离子浓度(由表1可知膜外和膜内钾离子浓度分别为5mol·m-3和140mol·m-3)。将数据代入能斯特方程可得：

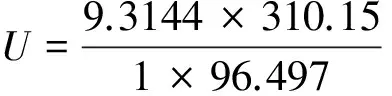
(2)

这说明，钾离子的静息电位大致为-90mV左右。

同理，将钠离子的离子浓度代入可得：

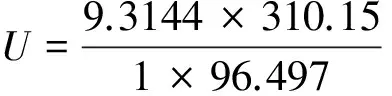
(3)

钠离子的平衡电位为60mV左右，在两个电位的影响下，静息电位应该在-90mV到+60mV之间。然而在静息状态下细胞膜对于钾离子是通透的，而对于钠离子通透性却很差，所以钠离子通道的电位只产生一个很小的影响，最后综合所有影响因素细胞的实际静息电位停留在-60mV～-70mV左右[6]。

2.2 动作电位

神经细胞最重要的特征并不是它有静息电位(大多数细胞都有)，而在于当刺激来临时它能产生一个电信号，并通过轴突传递出去来控制肌肉做出相应的反应。刺激可以来自各个方面，比如热刺激、化学刺激、压力、光线；也可以是来自大脑和脊髓的电信号刺激。如果刺激超过了一定的阈值，一个电压脉冲就会顺着轴突向前传导。这个脉冲电压的图像如图5所示。

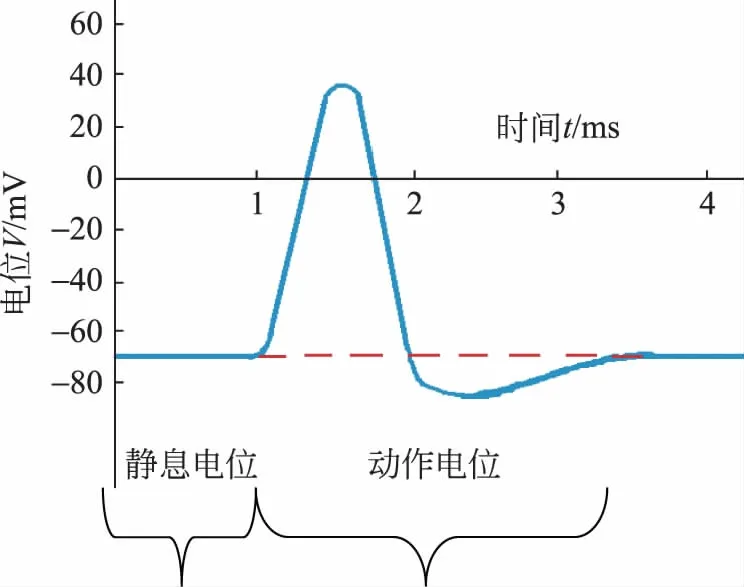
图5 动作电位的脉冲电压随时间变化图

由图5可知，电势差由静息电位-70mV增加到了+30mV或+40mV，动作电位持续大约1ms，在轴突上的传导速度约为30m/s到150m/s。是什么引起动作电位呢？在发生刺激的那一点，细胞膜将瞬间调整它的通透性，由静息状态下对钾离子具有通透性转变为对钠离子具有很大的通透性。当神经或肌肉细胞处于静息状态时，细胞膜外带正电，膜内带负电，这种状态又称极化。细胞受刺激所经历的去极化和复极化过程，伴随着电势差的波动过程。这种电势差波动称为动作电位。此时，钠离子通道会打开，由于静息状态下胞外钠离子浓度高于胞内浓度，在扩散作用和库仑力的作用下，大量钠离子涌入细胞内。这些钠离子首先中和了内部的负电荷，随着钠离子继续涌入使内膜电势变为高电势，这个过程我们称之为“去极化”。之后在很短的时间内，钠离子通道会迅速关闭，细胞膜上的钾离子通道随之打开，当钠离子通道关闭钾离子通道正好全部打开。由于胞内钾离子浓度大于胞外钾离子浓度，再加之库仑力的推动，此时大量的钾离子会涌入细胞外部，从而使细胞膜很快恢复到原来的静息状态，这个过程被称为“复极化”。整个过程可以看作一个电压脉冲，被称为动作电位[5]。

在钠通道打开时，钠离子迅速涌入细胞内，这样的离子定向流动的现象会导致电流的产生，而电流的大小可以用来衡量钠通道的开合情况。当电流很大的时候，钾通道处于完全打开的状态，而随着钠通道的关闭，电流也应随之减小。基于这个原理，英国科学家Hodgkin和Huxley通过测量动作电位发生时钠电流和钾电流随时间的变化来探究神经信号传导的原理。并通过数学拟合的方式用一组方程简明扼要地阐述了动作电位发生时钠钾通道的开合情况，这组方程被称为Hodgkin-Huxley方程[6]。

由欧姆定律可知，电流等于电压与电阻之比，而电导是电阻的倒数，所以电流可以用电导乘电压进行表示。以钾通道为例，即：Ik=gk(Vk-V)。其中，Ik为钾通道电流变化情况；gk为钾通道的电导；Vk为静息状态下钾通道产生的电势差(上文已通过能斯特方程计算约为-90mV)，而V为静息情况下细胞膜两侧的电势差。

Hodgkin-Huxley方程中有关描述钾电导的内容如下：

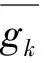
Hodgkin-Huxley中有关描述钠电导的内容如下：

根据Hodgkin-Huxley方程，我们可以用Matlab进行积分计算来仿真“动作电位发生”这个过程。将钠、钾两个方程组分步建立函数输入Matlab，利用迭代和对时间积分进行计算，并绘制10ms中钠钾电导的变化趋势图，其中常数的数值取自Hodgkin和Huxley于1952年发表的论文中表3中的原始数据[7]。仿真图如图6所示。

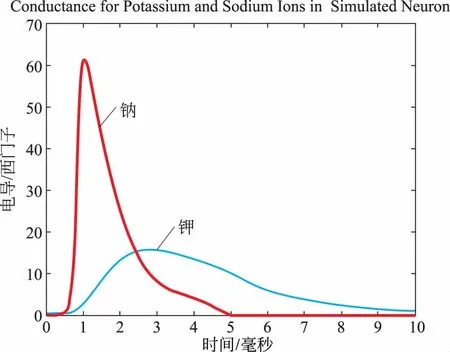
图6 Hodgkin-Huxley方程的Matlab仿真效果图

横轴代表时间(单位为ms)，纵轴代表电导(单位为西门子)，图上的二条曲线分别代表钠电导和钾电导的变化趋势。可以看出发生刺激时，钠电导先极速上升而后下降，即钠离子通道电阻先极速下降后上升，说明钠离子通道经过了一个先打开后关闭的过程；而钾电导在钠电导已经极速下降时还处于缓慢上升区，也就是说钾离子通道电阻逐渐下降，说明钾离子通道经过了一个从关闭到打开的过程，这与实验得到的结果完全相符。同时可以看到在大约2.5ms的时刻，当钠离子通道几乎关闭时钾离子通道正好完全打开。正如前文所论述的动作电位产生原理一样，去极化后极短时间内，钠通道会迅速关闭，细胞膜上的钾通道随之打开，当钠通道关闭时钾通道正好全部打开，此时大量钾离子涌出细胞，细胞膜很快恢复静息状态，完全符合复极化过程细胞膜的生理变化。用数学物理方法仿真出来的膜电位变化图像与实验测得的结果几乎完全吻合，说明我们的数学建模方法很好地模拟了神经动作电位的发生过程。

3 轴突的电容器模型

离子跨细胞膜流动时膜内外离子浓度会不会发生明显改变呢？下面我们视轴突为电容器进行分析。若轴突半径为10μm、长10cm，细胞膜的厚度为 10-8m，以钠离子为例计算其浓度变化情况。

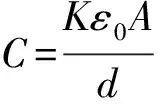
设圆柱形的表面积是A，半径为r，长度为l：

(15)

由上式可得：

(16)

电位由-70mV变为+30mV时，总变化量为100mV，则移动的总电荷量为

Q=CV≈(10-8F)×(0.1V)=10-9C

(17)

每个离子携带一个基本单位电荷e=1.6×10-19C，所以电位由-70mV变为+30mV时，移动的离子总量为

≈1010

(18)

轴突圆柱体的体积为

(19)

细胞内的钠离子的摩尔浓度由表1可知为15mol/m3，所以单位体积内钠离子数量为

15mol/m3=15×6.02×1023ions·m-3

(20)

因此，细胞内含有钠离子数为

(21)

一个动作电位之后，钠离子的数量改变为

×10-4

(22)

浓度改变非常微小，甚至将1000个动作电位叠加起来都不能显著改变钠离子浓度[8]。

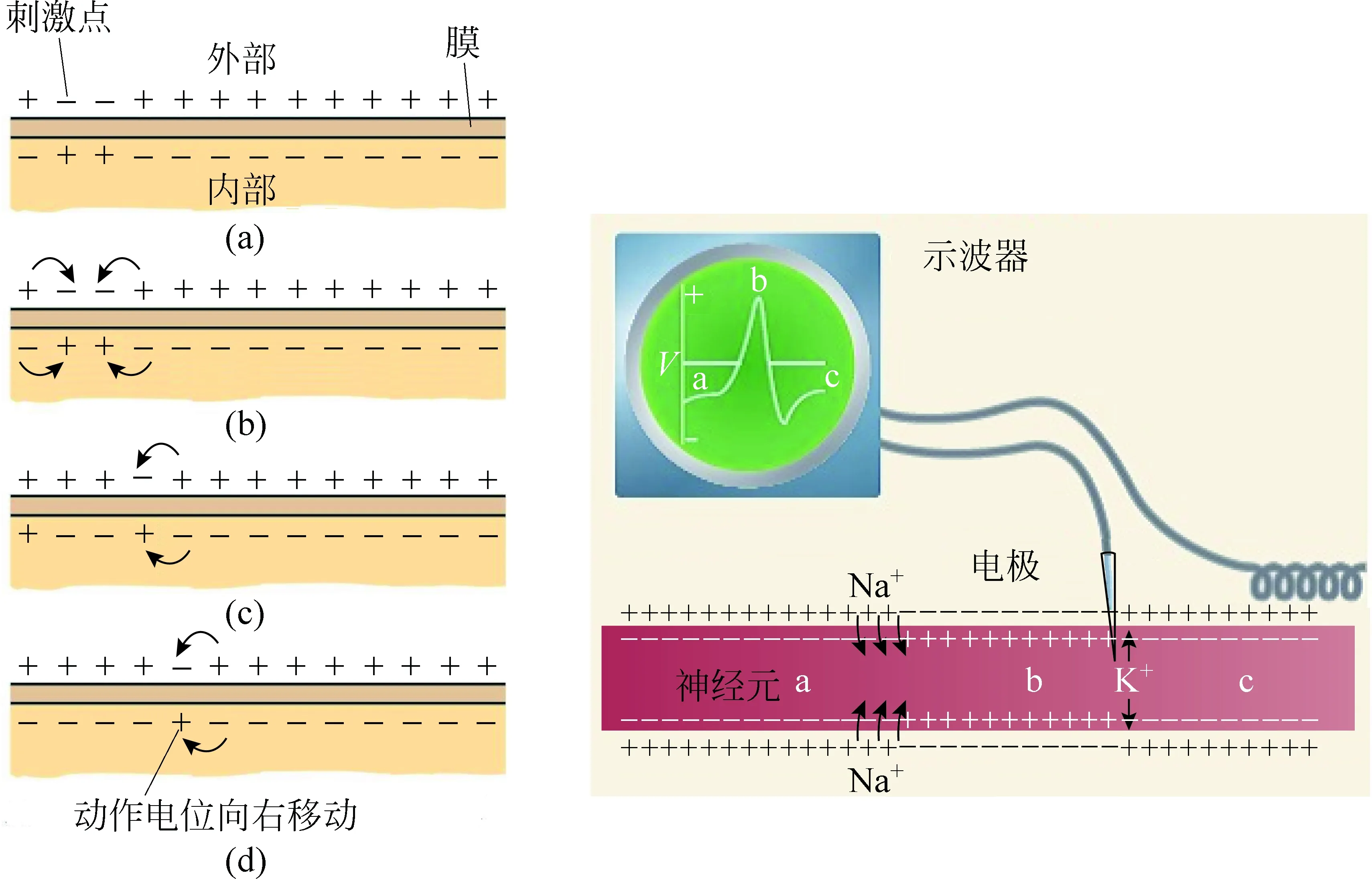
图7 神经传导电脉冲传导示意图[8,9]

4 神经系统电传导及其神经脉冲信号的传递

神经系统中的电流的产生和传导远比单纯的自由电子在导体中的移动要复杂得多，其中起关键作用的是库仑力和扩散作用。动作电位是细胞膜上的一个电脉冲，它如何在细胞膜，特别是沿着轴突，作为一个神经冲动而传导的呢？

变化着的电势差和电场使相邻的细胞膜的离子通透性发生改变，相同的过程重复发生，相邻的细胞膜被去极化，以此传递下去，从而影响更远处的细胞，动作电位在某个位置激发起一个神经冲动并沿着细胞膜缓慢传递。如图7所示，动作电位发生在刺激点，膜电位瞬间变为内正外负，附近的电荷被吸引到这个区域，这些相邻的位置电位差会下降，产生了一个动作电位。复极化后细胞膜上该点又恢复至原来的状态，而它附近的部分又去极化产生了一个动作电位，所以动作电位就沿着轴突传递下去了。

5 结语

本文从电学中基本概念电势差、电流、电容等出发，以人体神经系统为例，详细介绍神经系统中神经细胞内外的电势差(静息电位和动作电位)、轴突的电容器模型、神经脉冲信号的传递及其物理原理。旨在丰富读者关于电学中基本概念的理解和应用，体现了物理基本原理对其他交叉学科研究方法的重要指导意义。

[1] 张宪魁. 伽伐尼“动物电”的偶然发现[EB/OL][2003-11-03]. http://www.pep.com.cn/czwl/jszx/tbjx/tb8s/tb8s5/jc5/201008/t20100824_717367.htm.

[2] Serway R A, Faughn J S. College Physics[M]. 3 ed. Belmont, Calif.: Brook & Cole, Cengage Learning, 2006: 613-615, 623-625.

[3] Wikipedia. Neuron[EB/OL]. https://en.wikipedia.org/wiki/Neuron.

[4] Serway R A, Vuilly C. College Physics[M]. 9 ed. Brooks & Cole, Cengage Learning, 2012: 636.

[5] Urone P, Hinrichs R, Dirks K N. College Physics[M]. The Second Edition. OpenStax College, Connexions, Rice University, 2012: 494-497.

[6] 吴建永.鱿鱼巨大神镜与神经信号的秘密[J].物理,2013,42(8):580-588.

Wu J Y. The secrets of the sleeve-fish’s huge nerve and neural signals[J]. Physics, 2013， 42(8)： 580-588． ( in Chinese )

[7] Hodgkin A L, Huxley A F, A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve[M]//Physiological Laboratory, Cambridge: University of Cambridge, 1952-03-10.

[8] Giancoli D C. Physics[M]. The Sixth Edition. Pearson, 2014: 584-587.

[9] Gutkin B, Ermentrout G. Spikes too kinky in the cortex?[J]. Nature, 2006, 440: 999-1000.