基于GA-BP神经网络与敏感性分析的带钢厚度预测
2018-01-19唐秋华李维刚张利平
吴 倩,唐秋华,李维刚,张利平
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081;3.武汉科技大学信息科学与工程学院,湖北 武汉,430081)
带钢厚度合格率是衡量薄板带钢质量的重要指标,准确预测带钢厚度有利于适时调整轧制工艺参数,提高产品质量。传统方法通常是基于单品种单规格钢种进行带钢厚度预测,无法满足多品种多规格钢材同时生产的精度要求[1-2]。而合理利用钢材生产过程中的海量信息,探究产品质量、规格等数据与工艺参数之间的关系,能够为多品种钢材生产提供可靠的工艺调控方案。
利用人工神经网络进行钢铁产品各种性能指标的预测较为常见。Pouraliakbar等[3]采用人工神经网络对X70管线钢中热影响区的硬度进行预测。Singh等[4]建立了高磷钢的热变形模型,以温度、应变、应变率为神经网络输入来预测高磷钢流变应力。Tohidi等[5]利用人工神经网络预测受损钢件的弯曲强度。Chokshi等[6]建立了基于人工神经网络的相位分布预测模型,以研究热冲压下22MnB5硼钢的微观结构。常运合等[7]利用BP神经网络实现了对大方坯中间裂纹的在线预测。以上研究大多建立在传统神经网络的基础上,但传统神经网络存在收敛时间长、易陷入局部极值点等问题。将优化算法与神经网络进行融合可提高神经网络的预测精度,例如,利用遗传算法优化BP神经网络的方法已成功应用于主轴热误差的建模以及光伏输出功率的短期预测[8-9]。
另外,带钢生产工艺参数很多,而过多的输入参数会增加网络学习复杂度,影响预测精度,无法保证后续生产参数的快速、精准调控。因此在预测模型中引入敏感性分析,选出重要影响参数作为网络输入,这可能是一个有效的解决方案。
本文在研究遗传算法改进BP神经网络的原理基础上,结合企业实际生产数据,通过GA-BP神经网络实现对不同规格带钢的厚度预测,同时采用Tchaban算法[10]对工艺参数进行敏感性分析,筛选对带钢厚度影响较大的工艺参数作为网络输入,最后通过实验对所提出的带钢厚度预测方法的可行性和有效性进行验证。
1 融合GA-BP神经网络与敏感性分析的预测方法
1.1 GA-BP神经网络
传统BP神经网络在对数据样本进行训练时,其初始权值和阈值通常采用随机方法产生。若初始值选取不当,极易使神经网络的学习速率过慢而难以收敛,甚至陷入局部极值点。
遗传算法对神经网络的优化是在确定BP网络结构后,首先对网络各层间的初始权阈值进行实数编码,再经过选择、交叉、变异等遗传操作获取较优值,并将其作为神经网络的初始权阈值。遗传算法个体基因位数等于神经网络权阈值的个数,每位个体的适应度函数根据训练误差进行设计,计算公式如下:
∀i
(1)
式中:f(i)为第i个染色体的适应度值;p为神经网络训练样本数;yij表示第i个染色体对第j个样本的预测输出值;tij表示样本实际输出值。
1.2 基于Tchaban算法的敏感性分析
由于神经网络在自适应学习阶段主要是通过误差反馈来对权阈值进行调整,因此权值在一定程度上体现了输入对输出的影响和贡献。Tchaban算法的主要原理是通过神经网络各层之间权值相乘来进行敏感性分析,具体计算公式如下:
j=1,2,…,s;r=1,2,…,n
(2)
式中:Qir为输入参数xi对输出参数yr的敏感系数;wij为输入层与隐含层之间的连接权值;wjr为隐含层与输出层之间的连接权值;m、s和n分别表示输入层、隐含层和输出层的神经元节点数。利用式(2)可计算出不同输入参数对输出参数的影响贡献值。
1.3 预测方法的融合
首先通过GA算法优化BP神经网络权阈值,使BP神经网络有较好的预测性能。然后在训练好的GA-BP神经网络基础上,提取各层的连接权值,使用Tchaban算法对网络输入参数进行敏感性分析,判断各输入参数对输出参数的影响程度,可以为生产过程中的参数调控提供指导,同时用筛选出的重要工艺参数作为新的T-GA-BP神经网络输入,能有效降低网络复杂度,实现对产品性能指标的准确预测。
2 带钢厚度预测模型的设计
2.1 数据样本预处理
本文以某钢厂薄板坯连铸连轧生产线为研究对象建立带钢厚度预测模型。轧制过程中影响带钢厚度的因素较多,主要有连轧机组中F1~F7轧机的轧制力、活套张力、窜辊参数和轧辊磨损量以及出炉温度等29组工艺参数。经过对生产数据的分析发现,活套张力这7组参数均为标准值,故可将其从输入参数中剔除,以其余22组参数作为神经网络输入。
具有不同特征维度的样本数据,其表征含义和数量级也不同。而数据间相差太大的样本值在网络训练时会增加权值和阈值的调节难度。为使样本数据更具有典型性和优良的泛化能力,对其进行归一化处理,公式如下:
(3)
式中:x和x′分别表示数据归一化前后的值;xmin和xmax分别表示同一维度下参数的最小值和最大值。
考虑到带钢厚度数据的采集过程可能存在人为测量错误等异常情况,须对数据进行异常点检测。本文采用基于距离的异常点检测算法,其主要原理是通过衡量数据表中不同样本数据间的距离来判断数据点是否异常[11]。每一组训练样本视为效用点di={xi1,xi2,…,xib},i=1,2,…,a。针对a组b维的数据表而言,效用点B和C之间的距离公式为:
(4)
式中:k为任意正整数,k=1时计算距离为绝对值距离,k=2时计算距离为欧氏距离。
给定较小正数δ及经验临界值N,若Dk(dB,dC)<δ,则效用点B和C互为临近点。对于任意效用点,当其临近点个数小于N时记为异常点。采用该方法可对样本数据进行筛选,从而保证数据的准确性。
2.2 GA-BP神经网络结构参数设计
本文利用MATLAB工具箱进行神经网络结构参数设计,其关键是确定网络层数、隐含层神经元个数、激活函数、训练函数等内容。
(1)网络层数的选择。研究表明,当单隐含层无法达到预定效果时,可以通过适当增加隐含层数来提高精度,然而隐含层数目过多会导致网络的复杂度增加,因此隐含层一般不超过两层,即隐含层数目设为imin=1,imax=2。

(3)激活函数、训练函数。本文激活函数主要采用两种:S型正切函数tansig和线性函数purelin,训练函数采用trainlm。
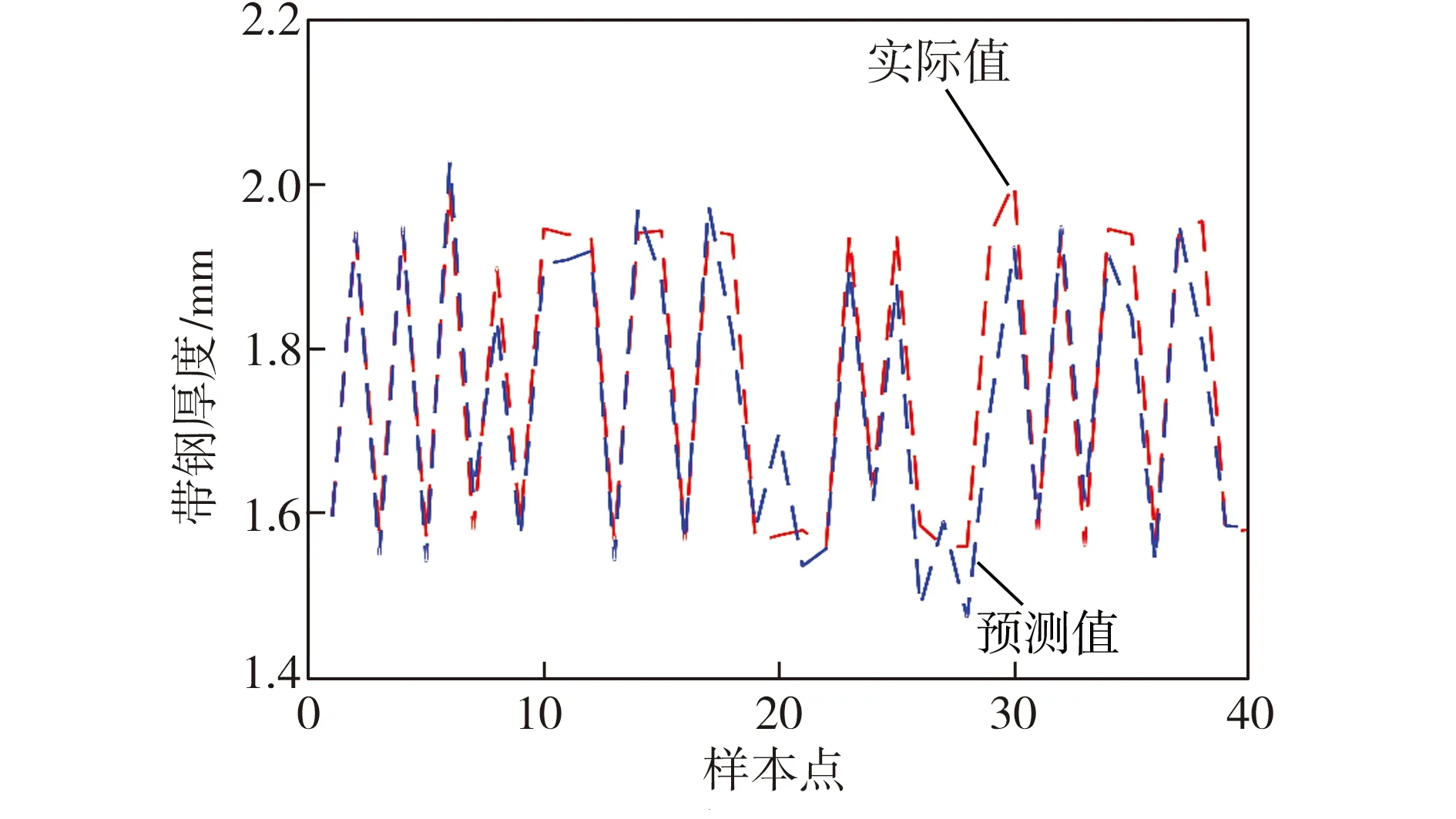
由于神经网络的层数及隐含层节点数有一定的取值范围,故通过如图1所示的循环迭代方式(最大迭代次数为100)确定为:采用单隐含层,隐含层神经元个数为10。

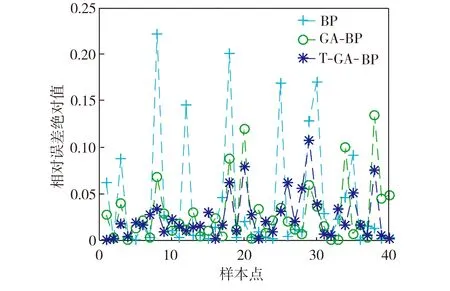
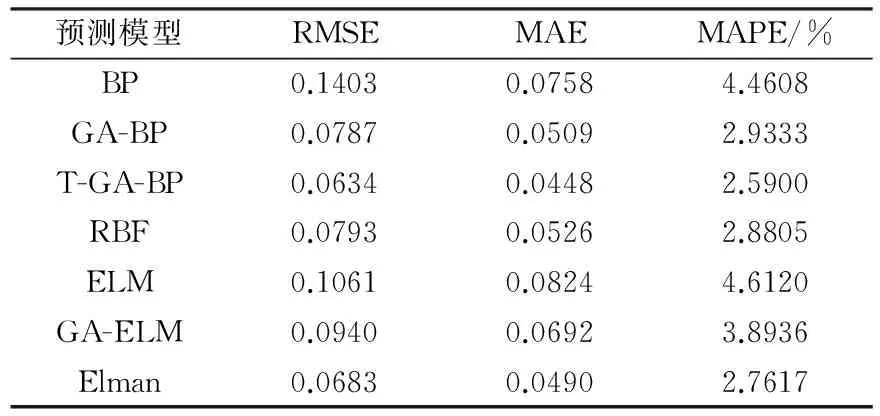
算法:BP神经网络隐含层结构的确定输入:训练样本输出:网络结构1:开始;2:读入训练样本;3:隐含层节点数s=smin,隐含层数目i=imin;4:网络训练;5:While(隐含层数目i 图1确定隐含层结构的流程 Fig.1Flowchartofdetermininghiddenlayerstructure 遗传算法的参数设置主要包括:遗传迭代次数maxgen=50,种群规模sizepop=10,交叉概率pcross=0.8,变异概率pmutation=0.1。遗传算子设计为:轮盘赌选择方法,双点交叉,单点变异。 图2所示为T-GA-BP神经网络建模流程,主要分为两阶段。第一阶段:首先对工艺参数进行数据筛选和归一化处理,获得22组输入参数,然后采用GA算法优化BP神经网络。第二阶段:从训练好的GA-BP神经网络中提取输入层、隐含层及输出层之间的连接权值,采用Tchaban算法计算轧制力等工艺参数对带钢轧制厚度的敏感系数,筛选出对带钢厚度影响较大的工艺参数,作为新的输入参数来训练T-GA-BP神经网络,并据此进行带钢厚度预测。 图2 T-GA-BP神经网络建模流程 本文实验采用的数据均来自带钢轧制生产现场。设置经过预处理后的500组数据作为训练样本,40组数据作为测试样本。 GA-BP神经网络权阈值的优化结果如图3所示。可以看出,最优个体的适应度函数值随迭代次数的增加而逐渐减小。由于GA算法的适应度函数表征BP网络训练样本误差的总和,因此最小适应度函数对应的个体即可作为BP神经网络的初始权阈值。 图3 适应度值迭代结果 采用Tchaban算法计算各输入工艺参数对带钢厚度的敏感系数,结果如表1所示。 表1 各工艺参数的敏感系数值 从表1可看出,敏感系数最大的两个工艺参数依次是F5和F3轧机的轧制力,这从带钢轧制工艺角度来分析是合理的,即影响带钢厚度的主要生产因素为轧制力。另外,对比其他轧机,F5轧机的轧制力和轧辊磨损量的敏感系数较大,因此F5轧机的性能对带钢厚度的轧制精度有重要影响。根据表1的分析结果,当生产计划发生变动时,可按各参数重要程度对轧机进行合理调整,从而满足带钢厚度的精度要求。 过多的输入参数会降低神经网络的泛化能力,从而影响其预测精度,因此根据敏感性分析结果,选取敏感系数大于4%的9个工艺参数作为神经网络的输入,通过训练得到T-GA-BP神经网络模型,将40组测试样本代入,得到带钢厚度预测值,如图4所示。 图4 基于T-GA-BP神经网络的带钢厚度预测值 Fig.4PredictedvaluesofstripthicknessbyT-GA-BPneuralnetwork 由图4可看出,带钢厚度预测值与实际值的拟合情况较优,表明本文方法具有较高的带钢厚度预测精度。 利用BP、GA-BP以及T-GA-BP三种神经网络预测模型分别对40组测试样本进行带钢厚度预测,各模型的预测误差如图5所示。 图5 三种神经网络模型的预测误差 分析图5可知,BP神经网络的预测误差值及波动性均最大;GA-BP神经网络预测误差值虽然较小,但整体波动较大;融合敏感性分析与GA算法的T-GA-BP神经网络预测误差值最小且波动较平稳。 为了进一步验证所提方法的有效性,下面再采用常用的径向基(RBF)神经网络、极限学习机ELM、GA算法改进后的极限学习机GA-ELM以及Elman神经网络预测模型对带钢厚度进行预测。为衡量预测精度,选用均方根误差RMSE、平均绝对误差MAE、平均绝对百分误差MAPE这3项指标对上述6种预测方法进行评价,具体数值见表2。 表2不同带钢厚度预测方法的评价指标 Table2Evaluationindexesofdifferentstripthicknesspredictionmethods 预测模型RMSEMAEMAPE/%BP0.14030.07584.4608GA-BP0.07870.05092.9333T-GA-BP0.06340.04482.5900RBF0.07930.05262.8805ELM0.10610.08244.6120GA-ELM0.09400.06923.8936Elman0.06830.04902.7617 一般认为MAPE<10%表明预测精度较高。由表2可知,上述预测方法的MAPE值均小于10%,其中MAPE<3%的预测模型有4种。 T-GA-BP的各项误差指标均低于其他预测方法对应值,表明该方法具有较好的学习拟合能力,可以通过各工艺参数对带钢厚度进行高精度预测。同时,经过GA算法优化后的BP神经网络和ELM神经网络模型的各项误差指标分别小于原始神经网络模型的对应值,表明遗传算法能在一定程度上提高神经网络的预测精度。总之,融合GA-BP神经网络与敏感性分析的T-GA-BP模型可有效预测带钢厚度,并且精度更高,同时基于Tchaban算法的参数敏感性分析结果能表明各参数对带钢轧制厚度的影响程度,可为后续生产参数的调整提供指导。 针对带钢厚度预测问题,本文在分析传统BP神经网络原理的基础上,采用遗传算法对网络权阈值进行优化,并根据Tchaban算法对带钢厚度影响因素进行敏感性分析,建立了融合GA-BP神经网络与敏感性分析的T-GA-BP带钢厚度预测模型。敏感性分析环节和遗传算法的加入不仅可以降低T-GA-BP神经网络的复杂度,还有效提高了其预测精度,对带钢厚度预控具有一定的参考价值。 [1] 彭开香,赖春山. 基于信息融合的带钢厚度预测控制[J].北京科技大学学报, 2011,33(3): 358-362. [2] 张飞,宗胜悦,谢新亮.基于KPLS的GM-AGC厚度预测方法[J].冶金设备, 2008(5): 8-12,7. [3] Pouraliakbar H, Khalaj M-j, Nazerfakhari M, et al. Artificial neural networks for hardness prediction of HAZ with chemical composition and tensile test of X70 pipeline steels[J]. Journal of Iron and Steel Research, International, 2015,22(5): 446-450. [4] Singh K, Rajput S K, Mehta Y. Modeling of the hot deformation behavior of a high phosphorus steel using artificial neural networks[J]. Materials Discovery, 2016,6: 1-8. [5] Tohidi S, Sharifi Y. Load-carrying capacity of locally corroded steel plate girder ends using artificial neural network[J]. Thin-walled Structures, 2016,100: 48-61. [6] Chokshi P, Dashwood R, Hughes D J. Artificial neural network (ANN) based microstructural prediction model for 22MnB5 boron steel during tailored hot stamping[J]. Computers and Structures, 2017,190: 162-172. [7] 常运合,曾智,张家泉,等.基于BP神经网络的大方坯质量在线预报模型[J].钢铁,2011,46(5): 33-37. [8] 马驰,杨军,梅雪松,等. 基于遗传算法及BP网络的主轴热误差建模[J]. 计算机集成制造系统, 2015,21(10): 2627-2636. [9] 许童羽,马艺铭,曹英丽,等.基于主成分分析和遗传优化BP神经网络的光伏输出功率短期预测[J]. 电力系统保护与控制, 2016,44(22): 90-95. [10] Tchaban T, Taylor M J, Griffin J P. Establishing impacts of the inputs in a feedforward neural network[J]. Neural Computing and Applications, 1998,7(4): 309-317. [11] 赵泽茂,何坤金,胡友进.基于距离的异常数据挖掘算法及其应用[J].计算机应用与软件,2005,22(9): 105-107.2.3 带钢厚度预测模型

3 实验分析


4 结语
