壁厚不均对平面内弯矩作用下P92钢管弯头蠕变寿命的影响

， ， ，

(华北电力大学,电站设备状态监测与控制教育部重点实验室，北京 102206)

0 引 言

管道弯头是电站高温蒸汽管道中的重要部件，由于特殊的结构和受力特征，使得其成为电站管道系统中最薄弱的环节之一。由于弯头长时间在高温高压环境下工作，因此蠕变失效成为其主要的失效形式。在管道制造过程中，弯头会存在一定的形状缺陷，如横截面壁厚不均等[1]。在设计过程中，弯头的寿命通常与直管的平均直径[2]有关，并未考虑壁厚不均的影响。因此，研究壁厚不均对弯头蠕变的影响，对电站弯头的寿命评估具有重要意义。

国内外学者对管道弯头蠕变的研究方法主要包括试验和有限元模拟两种。牛小驰等[3]利用损伤力学的方法分析了主蒸汽管道管线的损伤分布情况，发现弯头的损伤速率较直管的快，是整个管道的薄弱部位。李建等[4]对有局部减薄缺陷的P91钢管弯头的蠕变极限进行了有限元分析，提出了有局部减薄缺陷弯头的安全评定方法。ROUSE等[5]对壁厚不均的90°管弯头在内压载荷下的蠕变过程进行了数值模拟，结果表明壁厚不均导致的应力再分布对蠕变寿命有显著影响。HYDE等[6-7]对具有初始椭圆度和无初始椭圆度的90°弯头在内压载荷下的蠕变过程进行了有限元模拟，结果表明椭圆度引起弯头截面损伤位置发生变化，从而导致蠕变寿命缩短。GAMPE等[8]对带缺口的P91和P22钢管弯头进行了蠕变试验，分析了两种钢管弯头的蠕变裂纹萌生和扩展情况。NONAKA等[9]对9Cr1Mo钢再热弯头进行了全尺寸的内压蠕变试验，经超声波探伤仪检测发现蠕变裂纹最先出现在接近弯头内表面处，取平均直径处的应力所得到的单轴试验结果与全尺寸蠕变试验结果吻合。

军事英语的教学活动是一种创造性的建构活动，帮助学生习得语块就意味着向创造性的语言输出过渡。作为具有成熟分析能力的学习者，在这种创新性教学模式的引导下，通过对语块不断认知、总结和使用，学生一定能获得军事英语词汇生成规则并能创造性地产出和使用。

目前，国内外关于平面内弯矩载荷下弯头蠕变试验研究的相关报道较少。因此，为了研究壁厚不均对弯头蠕变寿命的影响，作者在平面内弯矩作用下P92钢管弯头高温蠕变试验的基础上，利用有限元方法模拟了不同壁厚不均度钢管弯头在平面内弯矩载荷下的高温蠕变过程，分析了弯头在不同位置处的应力和损伤情况，得到了弯头蠕变寿命与壁厚不均度之间的关系，为弯头蠕变寿命的评估提供了理论支持。

1 试样制备与试验方法

试验用管道为住友公司生产的P92钢直管和弯头，钢管平均直径168 mm，平均壁厚9 mm。采用氩弧焊在弯头两端焊接长度为300 mm的直管，焊接后进行高温热处理，保持焊口温度760 ℃，保温8 h，升温速率和冷却速率均小于100 ℃·h-1。P92钢的化学成分见表1，弯头的形状与尺寸见图1。

表1 P92钢的化学成分(质量分数)Tab.1 Chemical composition of P92 steel (mass) %

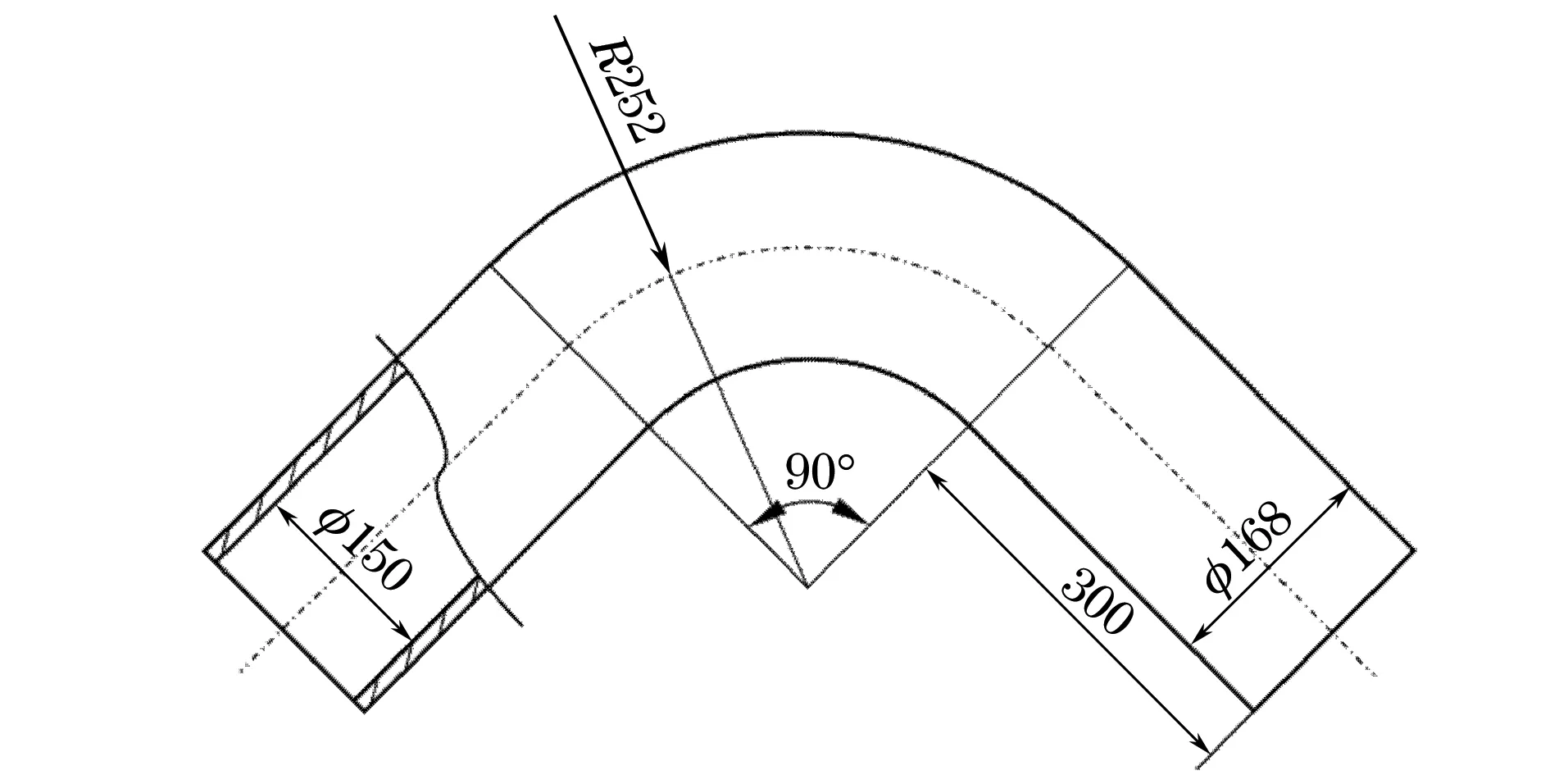
图1 P92钢管弯头的形状与尺寸Fig.1 Shape and dimension of P92 steel pipe bend

弯头的载荷是通过电机驱动丝杠来完成加载的，最大推力为300 kN，推力精度为±0.1 kN，能实现恒推力的持续加载，加载装置如图2所示。试验前为了预估所施加推力的大小，采用有限元软件ANSYS对不同推力条件下的应力分布进行模拟。对于壁厚均匀的弯头，弹性状态下的最大应力出现在侧弧内侧，当推力为50 kN时，最大应力为188 MPa，当进入蠕变阶段后，由于应力的再分布导致蠕变稳定阶段弯头的峰值应力降到135 MPa。因此，试验中采用的推力为50 kN，对弯头试样进行平面内弯矩作用下的高温蠕变试验，在试验过程中适当中断试验并进行相关数据的测试，直至试样被破坏，并与单轴蠕变试验结果[10]进行对比。采用履带式加热器，通过陶瓷绳包覆管道对其进行加热，如图3所示，取钢管中间截面为温度控制点，控制弯头部分温度为650 ℃。采用高温电阻应变片测弯头不同位置处的周向应变和轴向应变。

图2 加载装置示意Fig.2 Diagram of the loading device

图3 履带式加热器示意Fig.3 Diagram of the crawler heater

以弯头中心截面为对称面，沿弯头中心线选取5个截面，每个截面标记8个测试点，用于试验数据的测试，如图4所示。利用热电偶对试验过程中所有测试点的温度进行测试，采用高温电阻应变片对试验过程中管道OC截面上外弧、侧弧和内弧等3处(即图4中#1，#3或#3′，#1′位置)的应变进行测试。采用超声测厚仪测管道壁厚，测量精度为0.001 mm，分别在试验前、试验中断时(48%蠕变寿命)和试验后(100%蠕变寿命)测管道OC截面的壁厚。

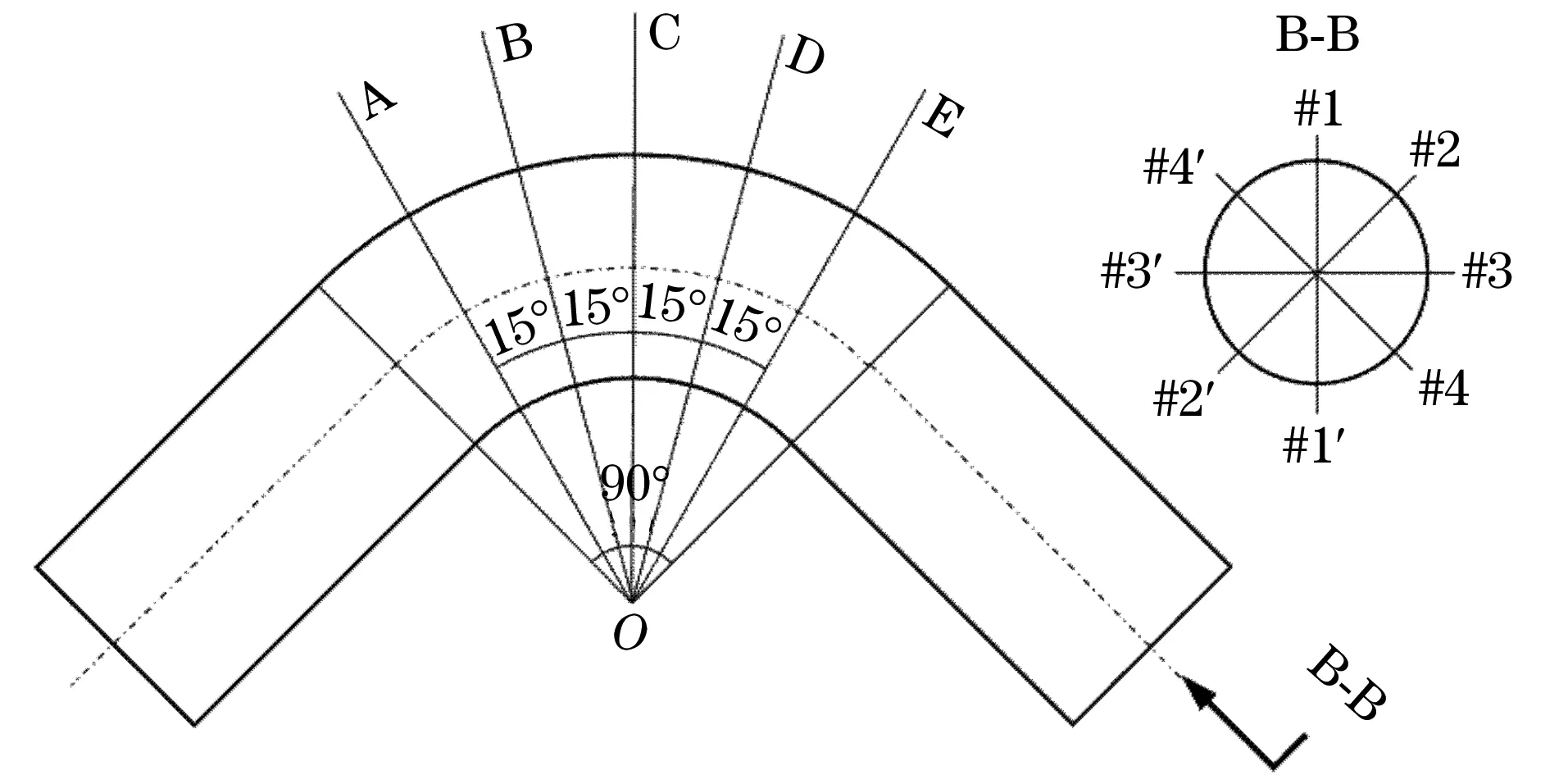
图4 测试点位置在钢管弯头上的分布Fig.4 Distribution of measurement positions on the steel pipe bend

2 试验结果

高温蠕变试验结果表明，弯头试样的蠕变寿命为278 h，而在其他试验条件相同的条件下，P92钢管弯头试样的单轴蠕变寿命为987 h[10]，这说明多轴应力加速了弯头的蠕变损伤速率，大大降低了弯头的蠕变寿命。

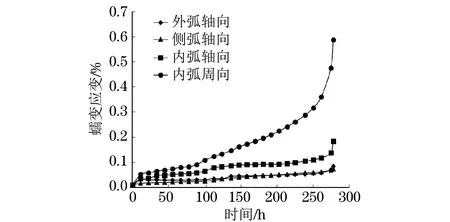
图5 钢管弯头OC截面处不同测试点的蠕变应变Fig.5 Creep strains of different measurement positions in OC section of the steel pipe bend

图6 钢管弯头壁厚在试验前和蠕变过程中的变化Fig.6 Changes of wall-thickness of the steel pipe bend before and during creep tests

由图5可知，在蠕变过程中，弯头内弧周向蠕变应变速率最大，最先发生失效，其次是侧弧和外弧位置。由图6可知：试验前弯头试样存在壁厚不均的情况，其中侧弧#3位置处的壁厚最小，侧弧#3′位置处的壁厚最大；在蠕变过程中，OC截面各处的壁厚均有所减小，试验前壁厚越小，试验后壁厚减小得越多，其中侧弧#3位置处壁厚减小得最多，这与管弯头因蠕变变形而导致应力再分布有关，说明壁厚不均会对弯头的蠕变寿命产生显著影响。

3 有限元分析

3.1 蠕变模型和弯头模型的建立

为了分析壁厚不均对在平面内弯矩作用下的弯头蠕变寿命的影响，对弯头的蠕变过程进行有限元模拟。由于弯头OC截面不同位置处的应力分布不均所形成的多轴应力状态会导致损伤分布不均，因此模拟中采用可描述非均匀蠕变过程的改进Kachanov-Robatnov模型[11-12]，该模型的表达式为

基于自调整因子模糊PID是在传统模糊PID的基础上改进模糊规则，实现控制规则的调整。仿真结果表明:基于自调整因子模糊PID在直流电机速度控制上具有更好的鲁棒性、抗干扰能力，能得到更好的控制效果。

σrep=ασI+(1-α)σe

(1)

将式(1)～(4)的蠕变模型嵌入到ANSYS软件的蠕变接口程序usercreep.f文件中进行二次开发，并对平面内弯矩作用下的弯头进行有限元分析。在计算过程中当损伤常数达到0.95时，认为蠕变寿命终结，自动停止有限元计算。由于弯头尺寸的对称性，对于外弧减薄的弯头，在进行有限元分析时只需对弯头1/4部分进行建模，弯头和直管段部分均采用扫略形式划分网格，其余部分采用自由网格划分，有限元网格划分及边界条件如图8所示。对于侧弧减薄的弯头，由于弯头两侧的壁厚不同，因此需要对弯头的1/2部分进行建模，有限元网格划分及边界条件与外弧减薄弯头的类似。为了模拟试验中的加载过程，在弯头端部连接孔的中心建立了一个节点，将其与孔壁设置为刚性接触，并在该节点上施加平面内的推力，使整个弯头受到平面内弯矩的作用，推力为50 kN。

(2)

该系统体积小，重量轻，成本低廉可应用于未来的光伏发电系统，只需依据光伏组件的实际数量做出具体调整即可.并且证明该系统使用的传感器测量的电流、电压信号的精度高、可靠性好.因为该传感器延时短可以即时发现光伏发电系统的故障节点，更加方便工作人员及时对光伏阵列进行维护与检修，进而在保证生产成本的基础上提高了光伏发电效率.

(3)

σI=max{|σ1|,|σ2|,|σ3|}

护理人员对患者未保持高度的重视和风险意识,常常忽略患者机体的细微变化[2],在患者出现突发状况时未及时给予有效的护理干预,导致患者的病情加重,延长住院时间,由于不能为患者提供良好的服务和帮助,常常会产生护理人员和患者之间的矛盾,同时在日常工作中护理人员未全面了解患者的文化水平等,导致护理人员与患者产生分歧和医嘱传达理解错误等情况发生,误认为护理工作者的技术素质与业务水平不过关[3],产生分歧,影响护患之间的关系,降低对护理的满意度。

(4)

外弧减薄的钢管弯头：

由图10可以看出：侧弧减薄钢管弯头的较高参考应力主要位于侧弧和内弧处。外弧减薄钢管弯头的参考应力分布与侧弧减薄的类似。由图11可知：在稳态蠕变阶段，外弧减薄钢管弯头的内弧和侧弧内表面的参考应力均与均匀壁厚钢管弯头的基本相同，而内弧和侧弧外表面的参考应力均明显低于均匀壁厚钢管弯头的；侧弧减薄钢管弯头的内弧和侧弧内表面和外表面的参考应力均高于均匀壁厚钢管弯头的，且管壁减薄侧的参考应力高于另一侧的。因此，钢管弯头不同位置处管壁的减薄导致了不同的应力分布，最大参考应力均位于侧弧内表面附近。

(5)

学生笔下的诗句比原诗更灵动，更有趣。有了范文引路，学生写起来言之有物，言之有序，既有仿效，又有创新，更重要的是通过仿写，学生掌握了作者的巧妙构思，为以后的写作打下了一定基础。

表2 650 ℃下P92钢的力学性能参数和蠕变模型参数Tab.2 Mechanical property parameters and creep model parameters of P92 steel at 650 ℃

图7 钢管弯头OC截面不同位置处的壁厚减薄示意Fig.7 Diagram of wall-thickness reduction in different locations in OC section of the steel pipe bend: (a) wall-thickness reduction in the extrados and (b) wall-thickness reduction in the flank

对不同管壁减薄形式和不同壁厚不均度的弯头在平面内弯矩作用下的蠕变过程进行了数值模拟，弯头OC截面的几何尺寸和壁厚不均度见表3。

式中：Ct为壁厚不均度；t为平均壁厚；tmin为最小壁厚。

污水的深度处理工艺的目的是进一步去除污水中经二级处理后剩余的污染物质，工艺的选择取决于二级处理出水的水质和所需达到的水质标准。二级处理出水中污染物质为有机物和无机物的混合体，有机物包括细菌、病菌、藻类及原始生物等。不论是有机物还是无机物，根据它们存在于污水中的颗粒的大小又可分 为 悬 浮 物 （＞1μm）、胶 体 （1μm ～1nm）和 溶 解 物 （<1nm），一般来说通过混凝沉淀等常规工艺可以去除悬浮物和胶体粒子。溶解性杂质必须通过某些非常规手段才能去除。

表3 不同壁厚不均度的钢管弯头截面尺寸Tab.3 Sectional dimension of the steel pipe bends withdifferent eccentricity

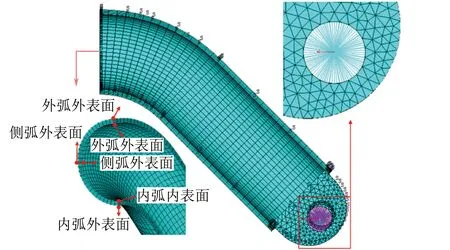
图8 钢管弯头的有限元网格划分和边界条件Fig.8 Finite element meshes generation and boundary conditions for the steel pipe bend

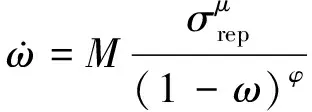
3.2 有限元模拟结果与分析

由图9可知：经过400 h蠕变试验后，壁厚均匀弯头的等效应力峰值从165 MPa减小为121 MPa，这说明在蠕变过程中，蠕变变形改变了应力的分布。结合式(2)和式(3)分析可知，等效应力决定着参考应力，从而影响损伤的分布。

文献[14]对热推和冷弯两种制造工艺得到的弯头进行研究，结果表明弯头的内弧、外弧和侧弧位置处(即图4中的#1′，#1，#3或#3′位置)均可能成为管壁减薄最严重的区域。结合文献[15]中对壁厚不均度的定义以及弯头的实际尺寸，将管壁减薄分为外弧减薄和侧弧减薄两种形式，如图7所示，图中R为钢管外径，r为钢管内径，h为偏心度。弯头的壁厚不均度可以采用式(5)进行描述。

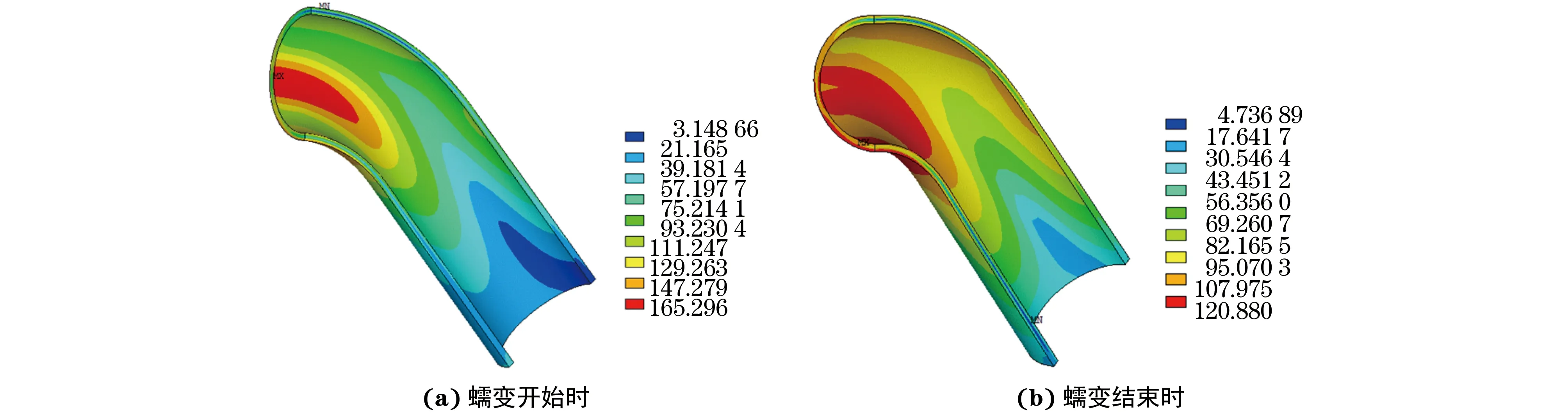
图9 均匀壁厚钢管弯头在蠕变开始和结束时的等效应力分布云图Fig.9 Effective stress distribution contours of the steel pipe bend with even wall-thickness at the beginning (a) and end (b) of creep

图10 侧弧减薄钢管弯头在稳态蠕变阶段的参考应力分布云图(50%蠕变寿命)Fig.10 Representative stress distribution contours of the steel pipe bend with wall-thickness reduction in the flank during stationary creep stage (50% creep lifetime)

由图12可知：对于均匀壁厚和外弧减薄的钢管弯头，在蠕变过程中最大参考应力均位于侧弧内表面；对于侧弧减薄的钢管弯头，在蠕变过程中侧弧减薄内表面和侧弧增厚内表面的参考应力最大，其次为内弧外表面。这与试验中测得的钢管弯头OC截面内弧处变形最大的结果一致。由图13可以看出，钢管弯头的最大损伤出现在侧弧内表面，这与最大参考应力的位置基本重合，说明钢管弯头首先从侧弧内表面开始失效。

图11 均匀壁厚和管壁减薄钢管弯头OC截面不同位置处内外表面的参考应力(50%蠕变寿命，h=2)Fig.11 Representative stresses at different positions in OC section of the steel pipe bend with even wall-thickness and different wall-thickness reduction (50% creep lifetime，h=2): (a)inner surface and (b)outer surface

4 试验验证

由模拟结果可以得到平面内弯矩作用下钢管弯头的蠕变寿命与壁厚不均度之间的关系，如图14所示。由图14可知：外弧减薄钢管弯头的蠕变寿命随壁厚不均度的增大而延长，且呈线性关系；侧弧减薄钢管弯头的蠕变寿命随壁厚不均度的增大而缩短，且缩短趋势逐渐减缓。由此建立壁厚不均度和钢管弯头蠕寿命tf之间的关系模型，关系式见式(6)～(7)。

对单轴蠕变试验数据进行处理可得到材料常数B，m，n0，n，A;采用蒙特-卡罗寻优法可求得材料常数M，μ和损伤常数φ;材料常数α可通过有限元模拟与缺口试样的蠕变试验来确定[13]。因此，650 ℃下P92钢的力学性能参数和蠕变模型参数见表2。

tf=302.4Ct+403.39

(6)

侧弧减薄的钢管弯头：

少先队员们在志愿活动中自主策划方案、自主践行活动、自主评价成果，不断促进自身主动地成长。自主，是少先队员当家做主的权利，是雏鹰日渐丰满羽翼的催化剂，是少先队员翱翔蓝天的力量源泉！

tf=479.24e-9.155Ct

(7)

由图14可知，试验得到侧弧减薄钢管弯头的蠕变寿命与壁厚不均度的关系满足式(7)。因此，试验结果验证了该关系模型的准确性，该关系模型可以准确地预测平面内弯矩作用下壁厚不均钢管弯头的蠕变寿命。

其中[α]是许用压力角。δmax、δmin的最大可取值区间是[0,180]，由式(12)前2式知α1、α2的最大可取值区间是[-90,90]，由式(13)、式(15)有

图12 均匀壁厚和管壁减薄钢管弯头不同位置处的参考应力在蠕变过程中的变化曲线(h=2)Fig.12 Change curves of the representative stress of different positions of the steel pipe bends with even wall-thickness (a) and different wall-thickness reduction (b-c) (h=2): (b) extrados reduction and (c) flank reduction

图13 均匀壁厚钢管弯头在蠕变后的损伤分布Fig.13 Damage distribution of the steel pipe bend with even wall-thickness after creep

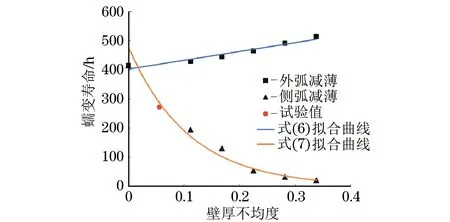
图14 平面内弯矩作用下钢管弯头的壁厚不均度与蠕变寿命的关系Fig.14 Relationship between eccentricity and creep lifetime of the steel pipe bend subjected to in-plane bending

5 结 论

(1) 壁厚不均的P92钢管弯头在平面内弯矩作用下的高温蠕变试验中，弯头内弧的蠕变应变速率较大，其次为侧弧和外弧位置的。

(2) 利用改进的Kachanov-Robatnov蠕变模型对不同壁厚不均度和不同管壁减薄钢管弯头的高温蠕变过程进行了有限元模拟，模拟结果与试验结果吻合，并得到了平面内弯矩作用下钢管弯头的蠕变寿命与壁厚不均度之间的关系。

(3) 外弧减薄钢管弯头的蠕变寿命随壁厚不均度的增大而延长，且呈线性关系；侧弧减薄钢管弯头的蠕变寿命随壁厚不均度的增大而缩短，且缩短趋势逐渐减缓。

(4) 建立了壁厚不均度和钢管弯头蠕变寿命之间的关系模型，试验结果验证了该关系模型的准确性，因此该关系模型可以准确地预测平面内弯矩作用下壁厚不均钢管弯头的蠕变寿命。

[1] CHERNIY V P. Effect of curved bar properties on bending of curved pipes[J]. ASME Journal of Applied Mechanics, 2001, 68(4): 650-655.

[2] YAGHI A H, HYDE T H, BECKER A A,etal. Parametric peak stress functions of 90° pipe bends with ovality under steady-state creep conditions[J]. International Journal of Pressure Vessels and Piping, 2009, 86(10): 684-692.

[3] 牛小驰, 巩建鸣, 姜勇, 等. 基于损伤力学的电厂主蒸汽管道蠕变损伤有限元分析[J]. 中国电机工程学报, 2008, 28(20): 32-37.

[4] 李建, 周昌玉, 薛吉林. 含内局部减薄缺陷高温弯管蠕变极限载荷及其安全评定[J]. 机械强度, 2015, 37(2): 348-354.

[5] ROUSE J P, LEOM M Z, SUN W,etal. Steady-state creep peak rupture stresses in 90° power plant pipe bends with manufacture induced cross-section dimension variations[J]. International Journal of Pressure Vessels and Piping, 2013, 105/106: 1-11.

[6] HYDE T H, SUN W, WILLIAMS J A. Life estimation of pressurised pipe bends using steady-state creep reference rupture stresses[J]. International Journal of Pressure Vessels and Piping, 2002, 79(12): 799-805.

[7] HYDE T H, YAGHI A, BECKER A A,etal. Finite element creep continuum damage mechanics analysis of pressurised pipe bends with ovality[J]. JSME International Journal Series A Solid Mechanics and Material Engineering,2002,45(1):84-89.

[8] GAMPE U, SELIGER P. Creep crack growth testing of P91 and P22 pipe bends[J]. International Journal of Pressure Vessels and Piping, 2001, 78(11): 859-864.

[9] NONAKA I, ITO T, TAKEMASA F,etal. Full size internal pressure creep test for welded P91 hot reheat elbow[J]. International Journal of Pressure Vessels and Piping,2007,84(1):97-103.

[10] 常愿, 徐鸿, 蓝翔. P92钢多轴蠕变本构模型的建立及验证[J]. 机械工程材料, 2017, 41(2):112-118.

[11] LECKIE F A, HAYHURST D R. Constitutive equations for creep rupture[J]. Acta Metallurgica, 1977, 25(9): 1059-1070.

[12] RABOTNOV Y N. Creep problems in structural members[M]. [S.l.]: North-Holland Publication Co., 1969.

[13] NI Y Z, LAN X, XU H,etal. Finite element analysis and experimental research on notched strengthening effect of P92 steel[J]. Materials at High Temperatures, 2014, 31(2): 185-190.

[14] 孙兰萍, 赵建平. 不等厚性对弯头应力分布影响的有限元研究[J]. 南京工业大学学报, 2006, 28(3): 49-52.

[15] MICHAEL T C, VEERAPPAN A R, SHANMUGAM S. Effect of ovality and variable wall thickness on collapse loads in pipe bends subjected to in-plane bending closing moment[J]. Engineering Fracture Mechanics, 2012, 79: 138-148.