单峰过载对2205双相不锈钢疲劳裂纹扩展速率的影响

，

(辽宁石油化工大学机械工程学院，抚顺 113001)

0 引 言

2205双相不锈钢是工业中应用最广的一种双相不锈钢，其组织中铁素体与奥氏体的体积各约占50%[1]。与铁素体不锈钢相比，2205双相不锈钢无室温脆性, 具有更好的塑性、韧性和耐晶间腐蚀性能;与奥氏体不锈钢相比，2205双相不锈钢具有更高的强度、更好的耐晶间腐蚀和耐氯化物应力腐蚀能力[2-3]。因此，2205双相不锈钢在石油化工、沿海建筑等领域[4-7]具有广阔的应用前景。疲劳交变载荷是这些领域中各种工程结构件和设备在服役过程中常见的载荷类型，也是使其发生失效的主要原因之一。工程结构件和设备在安装及运行过程中，常常会出现瞬时过载、超压等现象。过载对工程材料的影响很大，影响机制也非常复杂[8]。目前，学者对不同材料的过载效应进行了大量的研究[9-13]，但关于2205双相不锈钢的研究报道较少。为此，作者对2205双相不锈钢进行了不同过载比下的疲劳裂纹扩展试验，研究单峰过载对疲劳裂纹扩展速率的影响，这对2205双相不锈钢在具有瞬时过载环境中的工程安全应用具有一定意义。

1 试样制备与试验方法

试验材料为上海宝钢不锈钢有限公司生产的热轧态SAF 2205双相不锈钢钢板，厚度为12 mm，化学成分(质量分数/%)为0.02C，0.50Si，1.38Mn，0.026P，0.001S，22.30Cr，5.44Ni，3.13Mo，0.162N，余Fe，屈服强度为600 MPa，抗拉强度为790 MPa。在试验钢板上截取金相试样，经打磨、抛光后，用12 g K3Fe(CN)6，40 g NaOH，100 mL H2O配制的溶液沸腾后腐蚀40 s，在Leica Q500MW型正立式金相显微镜上观察显微组织。

按照GB/T 6398-2000《金属材料疲劳裂纹扩展速率试验方法》，在试验钢板上加工出标准三点弯曲(SEB)试样，其形状与尺寸如图1所示，试样的裂纹扩展方向与热轧钢板的轧制方向一致。在Instron8872型电液伺服疲劳试验机上进行疲劳裂纹扩展试验，采用恒幅载荷加载方式，波形为正弦波，频率为10 Hz，应力比为0.1。试验前采用较大的载荷预制疲劳裂纹，第一级力值范围为10 kN，三到四级逐级降力，每级降低10%～20%，最后一级降至力值范围4.5 kN，预制疲劳裂纹长约2 mm。预制完成后，开始试验并对试验数据进行采集，当裂纹扩展进入稳态阶段，且裂纹长度约为11 mm时施加单峰过载，然后继续循环加载。加载方式如图2所示，图中Pmax为循环加载的最大力，Pmin为循环加载的最小力，Poverload为单峰过载力。过载比γ的计算公式为

(1)

试验中γ分别取1.0,1.5，2.5和3.5。采用柔度法测裂纹长度，用七步递增多项式法拟合并计算稳态扩展阶段的疲劳裂纹扩展速率。采用NOVA NanoSEM430型扫描电镜(SEM)观察断口形貌。

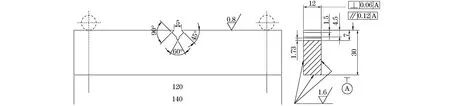
图1 三点弯曲试样的形状与尺寸Fig.1 Shape and dimension of three point bending specimen

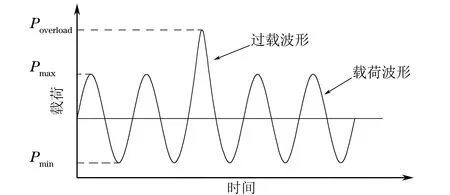
图2 加载方式示意Fig.2 Schematic of loading mode

2 试验结果与讨论

2.1 显微组织

由图3可知：试验钢的显微组织由铁素体和奥氏体组成；灰色组织为铁素体相，晶粒粗大且沿轧制方向被明显拉长；白色组织为奥氏体相，晶粒较细小且呈弥散分布；经图像分析发现，铁素体和奥氏体的体积比接近1∶1。

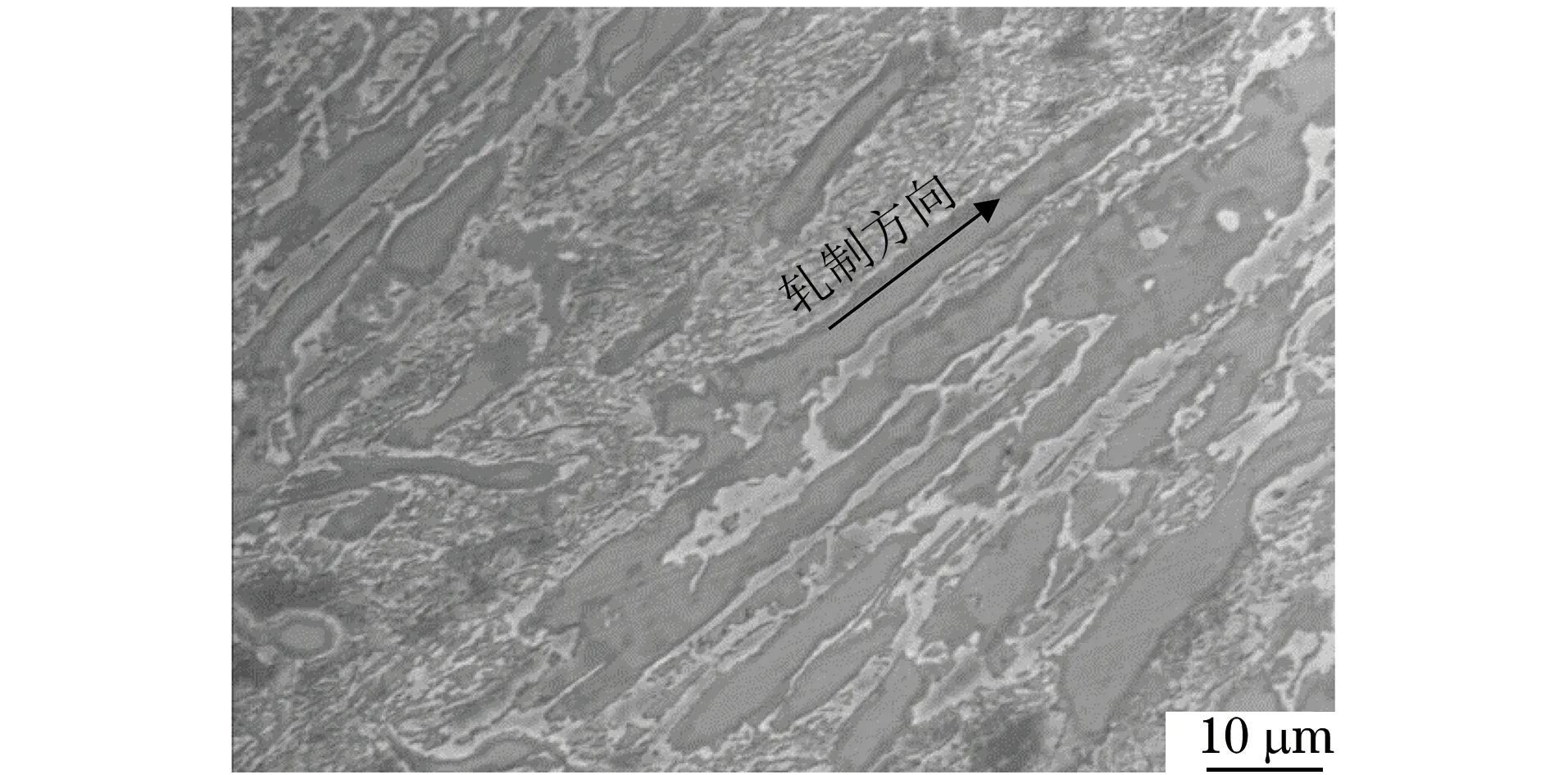
图3 试验钢的显微组织Fig.3 Microstructure of tested steel

2.2 疲劳裂纹扩展速率

图4中Nd为施加单峰过载后，裂纹继续扩展所需要的载荷循环次数。由图4可知：施加不同过载比的单峰过载后，试样的疲劳裂纹扩展曲线出现明显的“平台区”，此时裂纹长度出现停止增大甚至减小的现象，这表明裂纹扩展停滞甚至裂纹发生闭合；继续施加Nd周次循环载荷后，裂纹长度才继续增大；当γ为1.0，1.5，2.5时，Nd分别为0，14 363，218 743周次，即当γ<3.5时，随着γ的增大，Nd增加，裂纹扩展停滞的时间延长；当γ=3.5时，裂纹扩展完全停止，循环载荷继续加载至5×105周次时裂纹长度也未发生变化,这是由于单峰过载后，裂纹停止扩展，而试验机的数据采集系统以5×105次循环作为一个单点。由此可以看出，γ越大，试样的寿命越长。

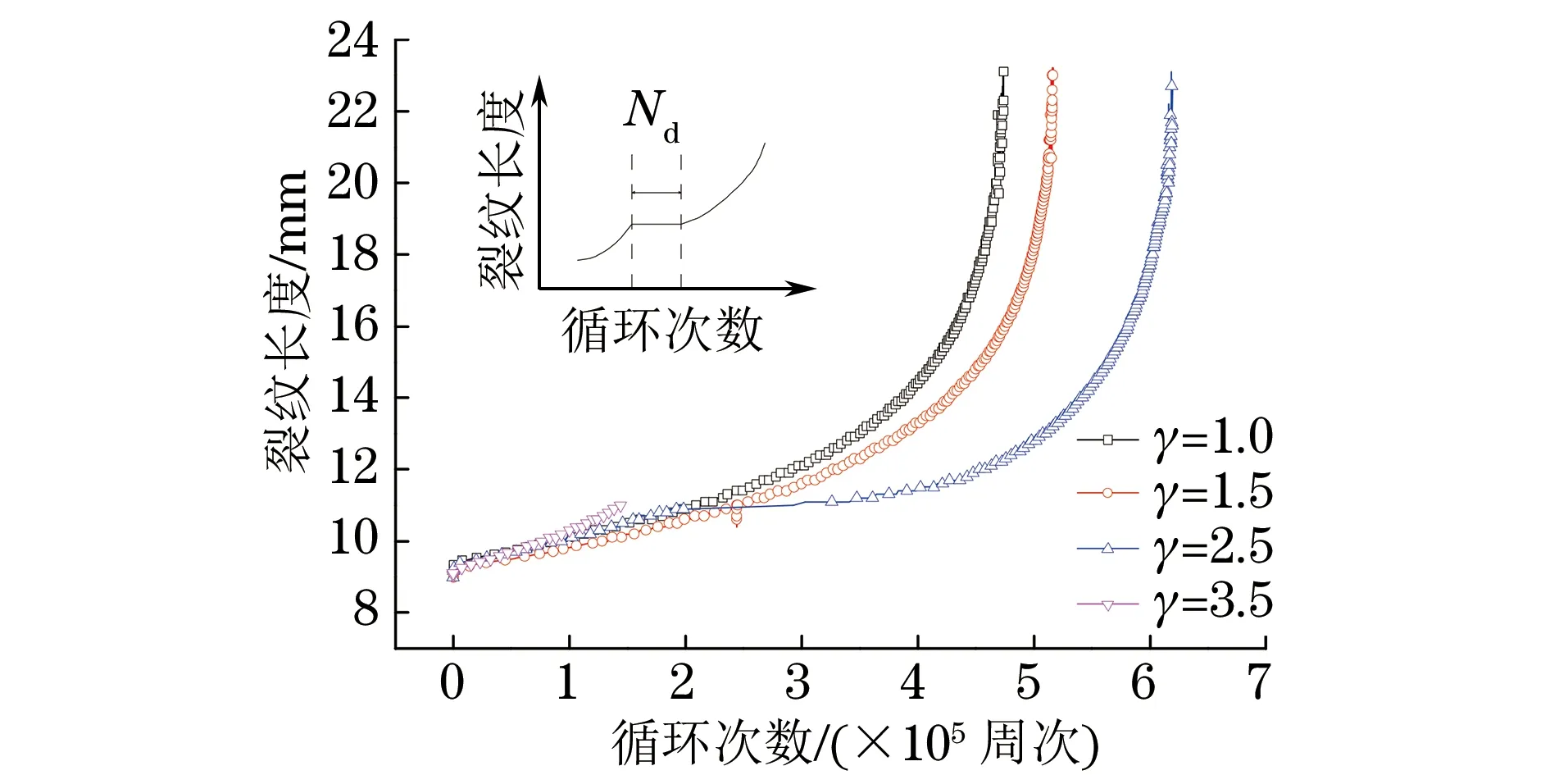
图4 不同过载比下试样的疲劳裂纹扩展曲线Fig.4 Fatigue crack propagation curves of samples at different overload ratios

由图5可知：当γ=1.0时，即未施加过载时试样的裂纹扩展速率曲线为一条直线；当施加单峰过载后，裂纹扩展速率显著下降，且γ越大，裂纹扩展速率下降的幅度越大；当γ=2.5时，裂纹扩展速率下降约一个数量级，继续加载一定周次后，裂纹扩展速率才逐渐恢复至稳态扩展时的速率；当γ=3.5时，施加单峰过载后裂纹扩展完全停止。

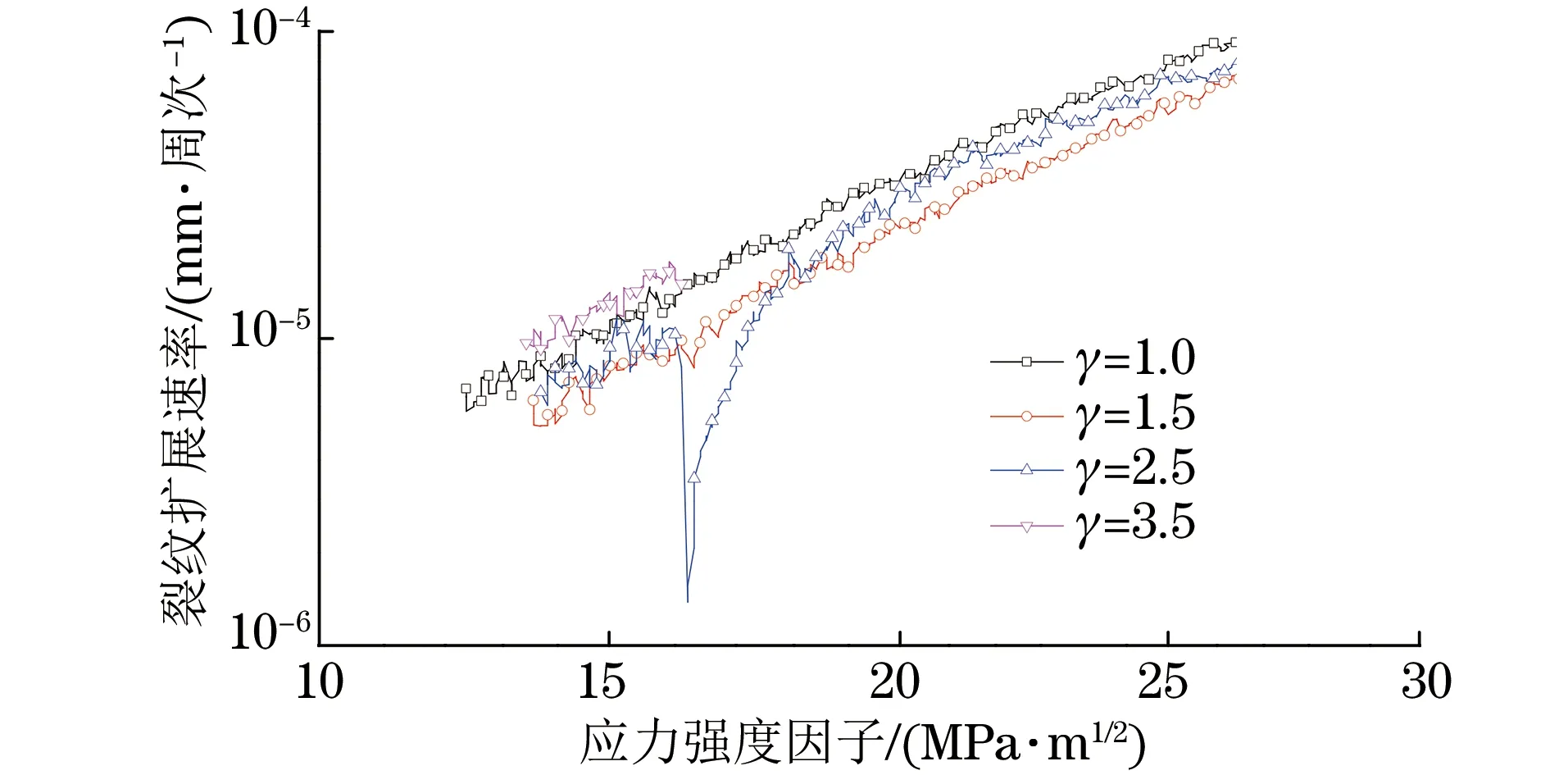
图5 不同过载比下试样的疲劳裂纹扩展速率曲线Fig.5 Fatigue crack propagation rate curves of samples at different overload ratios

表1中Δ(da/dN)为疲劳裂纹扩展速率的最大变化量，Ni为初始阶段裂纹扩展至0.25 mm所需要的循环次数[14]。由表1可以看出，Nd，Δ(da/dN)，Ni均随γ的增大而增大。

表1 不同过载比下试样的Nd，Δ(da/dN)和NiTab.1 Nd,Δ(da/dN), Ni of samples at differentoverload ratios

图6 不同过载比下试样疲劳裂纹尖端的表面形貌Fig.6 Surface morphology of the fatigue crack tips of samples at different overload ratios

由图6可知：当γ=2.5时，裂纹尖端明显钝化，裂纹仍保持在原有裂纹平面扩展；当γ=3.5时，裂纹尖端呈“Y”字型，裂纹尖端不再尖锐，出现裂纹偏折及开叉现象，裂纹不再沿原有裂纹平面扩展。

2.3 断口形貌

由图7可知：当裂纹扩展到11 mm时，在施加过载的位置出现了一条明显的分界线，该分界线为过载线，过载线左侧为未过载区域，右侧为过载塑性区；未过载区域的断裂形貌以准解理特征为主，河流花样明显，河流花样短而弯曲，且较密集；过载后，试样断口中出现较大的解理面和长而直的撕裂棱，断裂形式为解理断裂，河流花样变得稀疏，且长而直；过载线右侧出现了较多的微裂纹，推测是由于2205双相钢中的杂质在过载的作用下诱发而产生的；当裂纹穿过过载塑性区后，断口形貌又呈准解理特征。

2.4 分析与讨论

疲劳裂纹尖端因反向屈服而产生裂纹尖端塑性区及残余压应力场，在循环载荷的作用下，裂纹必须突破其尖端残余压应力场才能继续扩展[15]。JONES等[16]认为施加过载后，会在塑性材料裂纹尖端区域形成塑性强化区，当裂纹穿过塑性强化区时，会导致裂纹扩展速率下降。

图7 裂纹扩展到11 mm时试样的断口SEM形貌(γ=2.5)Fig.7 Fracture SEM morphology of sample with crack extended to 11 mm (γ=2.5): (a) at low magnification; (b) at relatively low magnification; (c) at relatively high magnification and (d) at high magnification

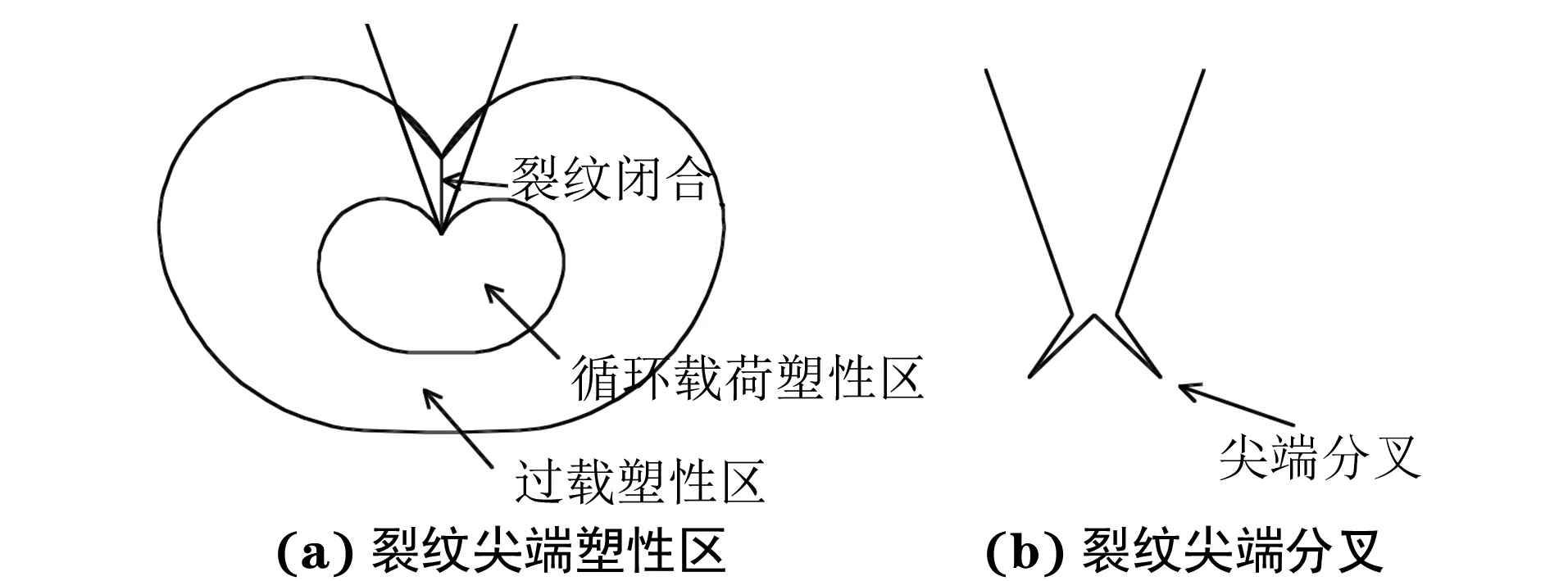
图8 裂纹尖端塑性区及分叉示意Fig.8 Schematic of plastic zone (a) and bifurcation at crack tip (b)

当γ<3.5时，裂纹在施加单峰过载后仍沿名义I型裂纹扩展平面扩展，但扩展速率明显下降甚至停滞，继续施加循环载荷Nd周次后，裂纹扩展速率才逐渐恢复至稳态扩展时的扩展速率，且随着γ的增大，Nd增加，裂纹恢复至稳态扩展的时间变长。裂纹扩展速率的下降甚至停滞是由过载导致裂纹尖端钝化或闭合引起的，如图8(a)所示。CHRISTENSEN[17]和RICE[18]提出，过载引起的裂纹尖端钝化犹如一个缺口，其应力集中比原来尖裂纹的小，该钝化甚至可以持续到过载后的裂纹扩展，从而导致裂纹扩展受到阻滞。ELBER[19-20]认为过载引起裂纹尖端形成超大塑性区，使裂纹尖端发生闭合，导致裂纹扩展停滞。随着γ的增大，裂纹尖端过载塑性区及残余压应力场范围增大，裂纹尖端钝化或闭合程度显著，裂纹穿过过载塑性区所需要的时间延长。裂纹一旦突破过载塑性区，裂纹扩展就会恢复到原来的稳态扩展阶段。

当γ=3.5时，施加单峰过载后，裂纹尖端发生明显偏折及分叉，裂纹扩展完全停止，继续循环加载至5×105周次后，裂纹扩展仍未见恢复。如图8(b)所示，过载引起裂纹尖端偏离名义I型裂纹扩展平面，发生分叉，使裂纹尖端有效应力强度因子范围大大降低，导致裂纹扩展完全停止，这符合TREBICKI等[21]和SOBCZYK等[22]提出的裂纹分叉机制。

3 结 论

(1) 单峰过载使得2205双相不锈钢中疲劳裂纹扩展出现明显的迟滞效应；过载比越大，裂纹扩展停滞的时间越长，疲劳裂纹扩展速率下降的幅度越大。

(2) 当γ<3.5时，单峰过载引起裂纹尖端发生钝化或闭合，导致疲劳裂纹扩展速率明显下降甚至停滞；当γ=3.5时，单峰过载引起裂纹尖端发生偏折及分叉，使裂纹尖端有效应力强度因子范围大幅度降低，疲劳裂纹扩展完全停止。

[1] 苏海滨.浅谈双相不锈钢及其应用[J].中国高新技术企业，2012(9)：62-63.

[2] 陆世英.不锈钢[M].北京：原子能出版社，1995.

[3] 吴玖.双相不锈钢[M].北京：冶金工业出版社，1999.

[4] 高娃，罗建民，杨建军，等.双相不锈钢的研究进展及其应用[J].兵器材料科学与工程，2005，29(3)：61-63.

[5] 张国信，李双权.双相不锈钢的性能及其在石化行业的应用[J].石油化工设备技术，2007，28(4)：55-59.

[6] 李京波，金学军.输油管道用316L和2205不锈钢低温蠕变模型的选择与验证[J].机械工程材料，2016，40(4)：55-57.

[7] 张文毓，侯世忠.国内外双相不锈钢的应用进展[J].装备机械，2015(3)：62-66.

[8] 郑修麟，王泓，鄢君辉，等.材料疲劳理论与工程应用[M].北京：科学出版社，2013：339-357.

[9] CREWS J H. Crack initiation at stress concentrations as influence by prior local plasticity[C]//Achievement of High Fatigue Resistance in Metals and Alloys. Philadelphia: ASTM, 1970: 37-52.

[10] BOISSONAT J. Fatigue of 7075-T6 aluminum alloy. Experimental research on the effects of static preloading on the fatigue life of structural components: ARL-64-55[R]. [S.l.]: Oxio, 1964.

[11] POTTER J M. Cyclic stress-strain behavior—Analysis, experimentation, and failure prediction[C]// American Society for Testing Materials. Philadelphia: ASTM, 1973: 109-132.

[12] SMITH I F C, HIRT M A. A review of fatigue strength improvement methods[J]. Canadian Journal of Civil Engineering, 1985, 12: 166-183.

[13] 郑修麟, 陈德广, 凌超. 疲劳裂纹起始的超载效应与新的寿命估算模型[J]. 西北工业大学学报, 1990, 8(2): 199-208.

[14] MADDOX S J. Fatigue analysis of welded joints using fracture mechanics[C]// Proceedings of International Conference and Exposition on Fatigue Corrosion Cracking，Fracture Mechanics and Failure Analysis. Salt Lake：ASM，1985：155-166.

[15] ALLISON J E.Measurement of crack-tip stress distribution by X-ray diffraction[J]. Fracture Mechanics，1979, 677:411-412.

[16] JONES R E. Fatigue crack growth retardation after single overload in Ti-6Al-4V titanium alloy [J]. Engineering Fracture Mechanics，1973，5(3)：589-604.

[17] CHRISTENSEN R H. Metal fatigue [M]. New York：McGraw-Hill，1959.

[18] RICE J R. Mechanics of crack tip deformation and extension by fatigue [C]//Fatigue Crack Propagation. [S.l.]：ASTM，1967:247-309.

[19] ELBER W. The significance of fatigue crack closure [C]// Damage Tolerance in Aircraft Structures. [S.l.]：ASTM，1971：230-242.

[20] ELBER W. Fatigue crack closure under cyclic tension [J]. Engineering Fracture Mechanics，1970，2(1)：37-44.

[21] TREBICKI J，SOBCZYK K. Curvilinear random fatigue crack growth: Effects of overloads[J].Fatigue and Fracture of Engineering Materials and Structures，2010, 19(2/3): 361-371.

[22] SOBCZYK K，TREBICKI J, SPENCER B F Jr. Modelling of the curvilinear random fatigue crack growth[J].Engineering Fracture Mechanics，1995,52(4): 703-715.