B4C陶瓷固-液协同烧结动力学和致密化模型

， ,， ，，，

(1.西北工业大学材料学系，西安 710072;2.中国兵器科学研究院宁波分院，宁波 315103; 3.西安航天复合材料研究所，西安 710000)

0 引 言

碳化硼(B4C)陶瓷是一种典型的结构陶瓷，具有密度低、耐磨和耐腐蚀性良好等优点，被广泛应用于航空航天、机械、核能、兵器等领域[1]。目前，国内外学者已经对陶瓷的烧结制备方法、微观组织和性能等进行了相关研究。随着研究的不断深入，涌现出了无压烧结、热压烧结、微波烧结等各种先进烧结工艺[2-6]。其中，无压烧结以其成本低、易于实现异形大尺寸产品的制备和工业化生产等优点而被认为是最具发展前途的一种烧结方法。在无压烧结过程中引入固液协同烧结助剂，如碳、金属氧化物(MgO、A12O3、Y2O3、TiO2等)[7-8]等，在烧结过程中形成一定比例的液相，通过固液协同作用加速传质过程，可以实现降低烧结温度、达到烧结致密化的目的。

陶瓷的烧结密度直接影响其微观组织和力学性能，并已成为陶瓷烧结工艺及其优化设计的主要评价指标[9-12]。文献[13-18]中分别研究了不同烧结方法、烧结助剂、烧结工艺参数等对碳化硼陶瓷烧结性能，尤其是对烧结密度的影响，但是烧结密度受到烧结方法、烧结温度、烧结时间、陶瓷压坯状态(配方和压坯密度)等的耦合作用，无法进行预测和精确控制。因此，如何通过众多因素的有效匹配、设计及控制来达到预期的烧结密度已成为该行业亟待解决的关键技术问题。为此，作者采用固-液协同烧结方法制备了不同原料配比和不同烧结参数下的碳化硼陶瓷，并计算和测试其理论密度、压坯密度和烧结密度。在此基础上，研究了烧结温度和烧结时间对碳化硼陶瓷线收缩率的影响、原料配比和烧结温度对表观活化能的影响，并进行了固-液协同烧结动力学分析；通过引入密度综合因子，建立了综合考虑烧结时间、烧结温度、原料配比、压坯密度的B4C陶瓷固-液协同烧结致密化模型，对该模型进行了精度分析，从而为实现碳化硼陶瓷烧结密度的有效控制提供预测方法，并为碳化硼陶瓷的工程应用奠定基础。

1 试样制备与试验方法

试验原料均为市售，包括：B4C粉，纯度大于97%，平均粒径不大于0.5 μm；化学纯Al2O3粉，粒径不大于0.5 μm；化学纯Y2O3粉，粒径不大于0.5 μm；SiC粉，纯度大于98%，粒径不大于0.5 μm；活性炭，比表面积不小于260 m2·g-1；酚醛树脂，固体质量分数约50%。按照表1中的配比将原料粉置于离心式喷雾干燥造粒机中进行碳化硼造粒，压力150 MPa，保压6 s，压成直径15 mm、高(20±0.1) mm的坯体。根据坯体的质量和体积，可计算出压坯密度ρ0分别为1.65，1.66，1.67，1.68 g·cm-3。

表1 B4C陶瓷试样的原料配比(质量分数)Tab.1 Raw powder ratios of B4C ceramicsamples (mass) %

将坯体置于ZSG-0.2-500W型真空无压烧结炉中进行烧结，该烧结炉的有效加热区尺寸为φ220 mm×500 mm，真空度为5×10-2Pa。当炉温低于1 873 K时，炉内真空度控制为10～600 Pa；当炉温达到1 873 K时，通入氩气保护气体。烧结温度分别为2 383，2 413,2 443，2 473 K，烧结时间分别为30，40,50，60 min。

采用阿基米德排水法测陶瓷的烧结密度ρ，采用混合法则[19-20]计算出不同配比的理论密度ρm，结果见表2。

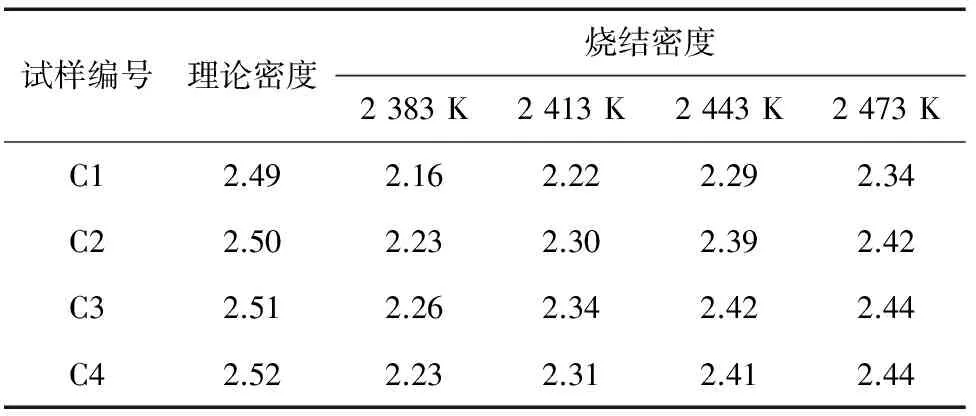
表2 B4C陶瓷试样的理论密度和烧结密度(烧结时间60 min)Tab.2 Theoretical density and sintering density of B4C ceramicsamples (sintering time of 60 min) g·cm-3

2 试验结果与讨论

2.1 B4C陶瓷固-液协同烧结的线收缩率

根据粉末烧结综合作用理论，对B4C陶瓷的线收缩率、烧结时间、密度、烧结温度之间的关系进行拟合，得到固-液协同烧结致密化模型，其中线收缩率、烧结温度、烧结时间之间的关系[21-22]为

(1)

两边取对数为

(2)

式中：ζ为线收缩率；A为与烧结温度有关的常数；t为烧结时间；n为特征指数；ΔL为试样长度的改变量；L为试样长度。

根据线收缩率测试结果和式(2)，得到不同B4C陶瓷试样在不同烧结温度下的线收缩率和烧结时间的关系，如图1所示。

由图1可以得到n和lnA的大小。因此，C1试样在不同烧结温度下的线收缩率与烧结时间之间的关系可以表示为：

当烧结温度为2 383 K时

lnζ=0.098 53lnt-2.159 66

(3)

当烧结温度为2 413 K时

lnζ=0.122 76lnt-2.198 93

(4)

图1 不同烧结温度下B4C陶瓷试样lnζ与lnt的拟合曲线Fig.1 Fitting curves of lnζ versus ln t of B4C ceramic samples at different sintering temperatures

当烧结温度为2 433 K时

lnζ=0.078 77lnt-1.974 87

(5)

当烧结温度为2 473 K时

lnζ=0.112 16lnt-2.091 18

(6)

同理，可以得到其他陶瓷试样在不同温度下的线收缩率和烧结时间之间的关系。

2.2 B4C陶瓷固-液协同烧结的表观活化能

阿伦尼乌斯最早提出了活化能概念，并认为化学反应的发生取决于活化分子之间的碰撞。活化能又称阈能，表示化学反应的能垒高度，是发生化学反应所需最小能量的度量。活化能越低，化学反应越易进行。阿伦尼乌斯提出的活化能表达式[23-24]为

(7)

K=1/t

(8)

式中：K为反应速率；T为烧结温度；R为气体常数；E为表观活化能；B为阿伦尼乌斯常数。

式(7)和式(8)忽视了温度对分子运动的影响，存在一定的局限性。联立式(7)和(8)，可获得烧结时间、烧结温度和活化能之间的关系，公式为

(9)

根据式(2)～(8)，得到n(lnζ-lnA)与1/T的线性关系拟合曲线(见图2)，从而得到E/R，并由此计算出表观活化能。由表3可知：相同烧结温度下，不同陶瓷试样的表观活化能不同；同一陶瓷试样在不同烧结温度下的表观活化能不同，烧结温度对表观活化能的影响比较明显。

表3 不同烧结温度下B4C陶瓷试样的表观活化能Tab.3 Apparent activation energy of B4C ceramic samples atdifferent sintering temperatures kJ·mol-1

陶瓷在烧结过程中的表观活化能很大程度上可以描述为生成中间络合物所消耗的能量。在烧结过程中，随着烧结时间的延长、烧结温度的升高，Al2O3和Y2O3等形成液相或固-液相的活化分子数量增多及分子运动碰撞的几率增大，使烧结过程中的传质更易于进行。与文献[19-23]中常压烧结方法下B4C陶瓷的烧结温度(2 173～2 473 K)和活化能(298.4 kJ·mol-1)相比，固-液协同烧结能够明显降低其烧结温度和表观活化能。

结合表3中的表观活化能，采用三次多项式研究了烧结温度对不同陶瓷试样表观活化能的影响，其表达式为

E=g0+g1T+g2T2+g3T3

(10)

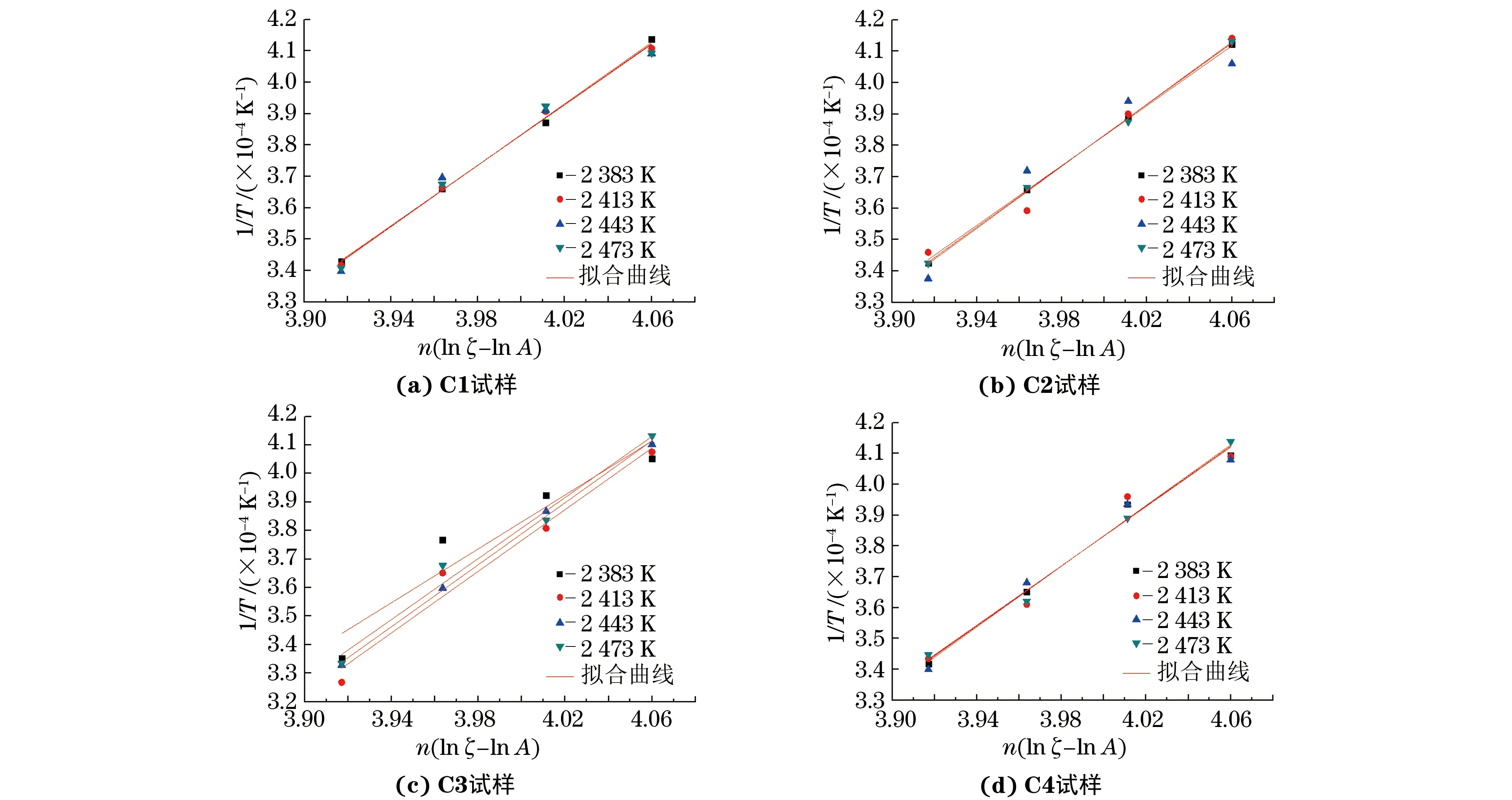
图2 不同烧结温度下B4C陶瓷试样n(lnζ-lnA)与1/T的线性关系拟合曲线Fig.2 Linear relationship fitting curves of n(lnζ-lnA) and 1/T of B4C ceramic samples at different sintering temperatures

式中：g0，g1，g2，g3为表观活化能的三次多项式拟合系数。不同B4C陶瓷试样表观活化能的三次多项式拟合系数见表4。

表4 不同B4C陶瓷试样表观活化能的三次多项式拟合系数Tab.4 Fitted coefficients of cubic polynomial for apparentactivation energy of different B4C ceramic samples

2.3 B4C陶瓷固-液协同烧结动力学

结合粉末烧结综合作用理论[25]，理论密度、烧结密度、压坯密度与烧结温度的关系为

(11)

式(11)可以表示为

(12)

式中：a和b分别为线性拟合曲线的斜率和截距。

结合式(9)，可获得不同B4C陶瓷试样的密度与表观活化能和烧结时间的关系，见式(13) 和(14)。

(13)

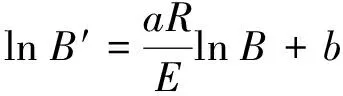
(14)

表5为C1试样的参数，由此可以得出，C1试样的固-液协同烧结动力学方程为

(15)

同理，可以获得其他试样的参数和固-液协同烧结动力学方程。

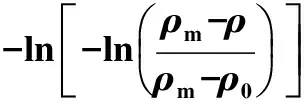
表5 C1试样的与lnt线性拟合参数Tab.5 Linear fitting coefficient of -lnand lnt of C1 sample

2.4 B4C陶瓷固-液协同烧结致密化模型

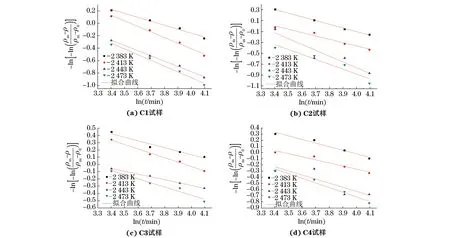
图3 不同陶瓷试样与lnt线性拟合曲线Fig.3 Linear fitting curves of -ln versus ln t of different ceramic samples

密度是陶瓷烧结效果评价的关键因素之一，直接决定着烧结体的力学、压电性等性能，因此实现密度控制烧结是陶瓷烧结领域中亟待解决的关键技术问题。影响烧结密度的主要因素有原料配比(C)、压坯密度，烧结温度、烧结时间等。因此，烧结密度可以表示为上述因素的函数。其中，原料配比直接决定着烧结体的理论密度，是理论密度的显函数，同时还对表观活化能有一定的影响，可以认为是表观活化能的隐函数，因此可以将烧结密度和表观活化能描述为

ρ=f[C(ρm，E),ρ0,t,T]

(16)

E=f(C,T)

(17)

引入密度综合因子γ，γ与烧结密度、理论密度和压坯密度的关系为

γ=(ρm-ρ0)/(ρm-ρ)

(18)

(19)

结合粉末烧结相互作用理论和动力学方程，致密化模型可以表示为综合考虑烧结温度、烧结时间和表观活化能的函数，其表达式为

(20)

在阿伦尼乌斯活化能的基础上，考虑烧结温度对拟合参数的补偿作用。采用三次多项式进行回归补偿拟合，E，a，b和lnB的烧结温度补偿多项式可以表示为

(21)

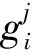
根据表5中C1试样的拟合参数a，b和lnB，分别拟合出烧结温度补偿多项式a(T)、b(T)和lnB(T)，C1试样的拟合曲线及拟合参数分别见图4和表6。

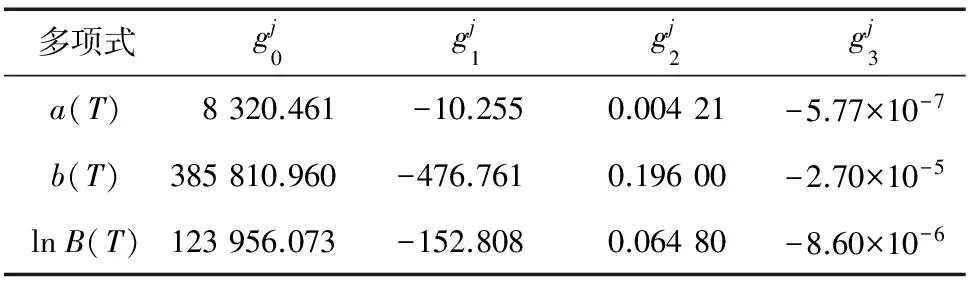
表6 C1试样的烧结温度补偿多项式的拟合系数Tab.6 Fitted coefficients of sintering temperaturecompensation polynomial of C1 sample

在此基础上，可建立综合考虑烧结时间、烧结温度、原料配比、压坯密度的B4C陶瓷固-液协同烧结致密化模型，其表达式为

(22)

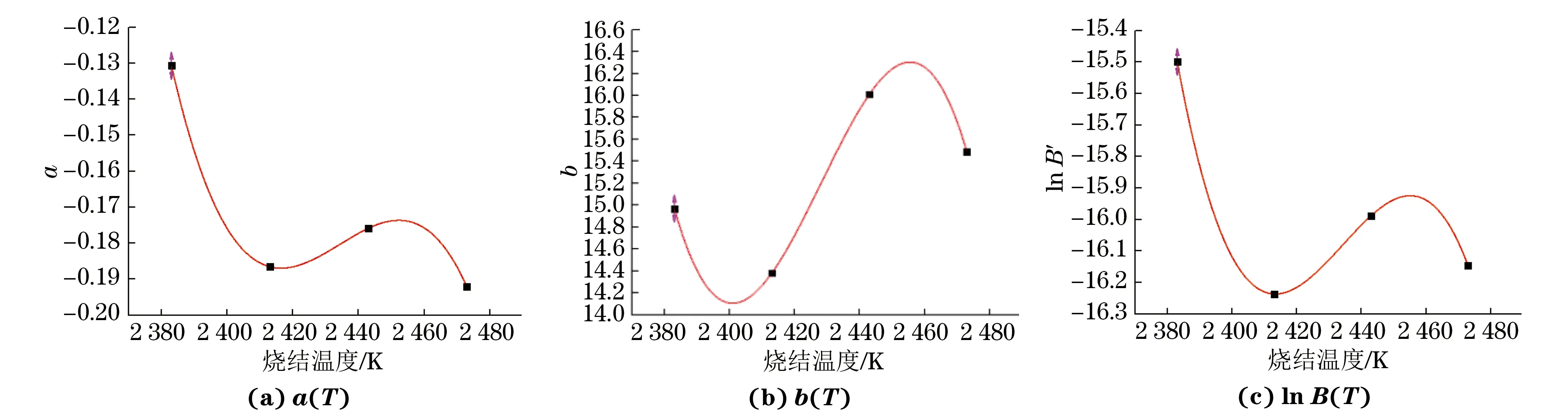
图4 C1试样不同拟合参数的烧结温度补偿拟合曲线Fig.4 Fitted curves of different fitting parameters considering temperature compensation of C1 sample

式中：f1=a(T)，f2=E(T)，f3=lnB(T)和f4=b(T)。

为了验证该致密化模型的准确性，采用数值统计方法，以平均相对误差绝对值(W)和相关系数(Re)作为模型精度评估的指标，对该模型进行了精度分析。

(23)

(24)

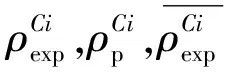
由图5可知：C1,C2,C3和C4试样的相关系数分别为0.968 7，0.935 3，0.936 3，0.905 6，这表明考虑烧结温度补偿的固-液协同烧结致密化模型的烧结密度预测值和烧结密度试验值之间具有较高的正相关性；平均相对误差绝对值分别为14.1%，18.2%，18.9%，18.3%，这表明该模型能够较好地描述B4C陶瓷固-液协同烧结过程中烧结密度与烧结时间、烧结温度及原料配比的关系。

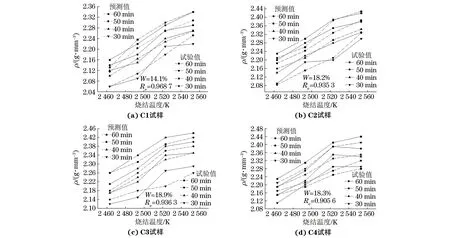
图5 B4C陶瓷烧结致密化模型的烧结密度预测值和烧结密度试验值的对比Fig.5 Comparison between predicted values by sintering densification model and tested values of sintered density of B4 ceramics

3 结 论

(1) 通过固-液协同烧结动力学研究，建立了不同烧结温度下B4C陶瓷的线收缩率与烧结时间之间的线性关系和烧结动力学方程；计算出了不同烧结温度下B4C陶瓷的表观活化能。

(2) 构建了综合考虑烧结温度、烧结时间、原料配比、压坯密度的B4C陶瓷固-液协同烧结致密化模型；考虑烧结温度补偿的固-液协同烧结致密化模型的烧结密度预测值和烧结密度实测值之间均具有较高的正相关性，且两者的平均相对误差绝对值小于20%，该模型能很好地描述B4C陶瓷固-液协同烧结过程中烧结密度与烧结时间、烧结温度、原料配比的关系。

[1] 黄培云，金展鹏，陈振华.粉末冶金基础理论与新技术[M].长沙:中南工业大学出版社，1997.

[2] 蒋国新,王声宏.碳化硼的低温热压[J].粉末冶金技术，1995,13(2):108-111.

[3] 祝宝军,肖汉宁.碳化硼陶瓷活化烧结技术进展[J].硬质合金，2004, 21(2):116-120.

[4] 王君.无压烧结碳化硼的研究进展[J].陶瓷，2008(1):13-20.

[5] LEE H, SPEYER R F. Pressureless sintering of boron carbide[J]. Journal of the American Ceramic Society, 2003,86(9):1468-1473.

[6] 印红羽，盛挺，汪海宽.硬质合金低压热等静压烧结工艺[J].粉末冶金技术,1997,15(4):299-303.

[7] 姚义俊,丘泰. Y2O3, La2O3, Sm2O3对氧化铝瓷烧结及力学性能的影响[J].中国稀土学报,2005,23(2):156-161.

[8] 杨秋红. La2O3对氧化铝透明陶瓷显微结构和透光性能的影响[J].中国稀土学报,2005，23 (6):713-715.

[9] 郑永挺, 韩杰才, 杜善义.燃烧合成AlN-TiC陶瓷及致密化机理分析[J]. 无机材料学报, 2000, 15(4):625-630.

[10] 孟范成, 张帆, 傅正义.燃烧反应加压法制备细晶氧化铝陶瓷的致密化机理[J]. 硅酸盐学报, 2010, 38(2):276-282.

[11] 黄晓巍. 液相烧结氧化铝陶瓷的致密化机理[J]. 材料导报, 2005, 19(增刊1):393-394.

[12] 张辉,穆柏春.影响碳化硼陶瓷致密化的因素[J].辽宁工学院学报，2005, 25(6):378-381.

[13] 王岭, 陈大明, 张虎,等. SPS制备致密碳化硼陶瓷的结构及性能[J]. 稀有金属材料与工程, 2009, 38(增刊2):529-532.

[14] 王零森, 尹邦跃, 方寅初. 成形剂对碳化硼压坯密度和烧结密度的影响[J]. 中南大学学报(自然科学版), 2002, 33(4):377-379.

[15] 袁义鹏, 姜宏伟, 郑友进. 葡萄糖助剂对无压烧结碳化硼性能的影响[J]. 牡丹江师范学院学报(自然科学版), 2016(3):36-38.

[16] 岳新艳, 应伟峰, 喻亮,等. B4C陶瓷材料的无压烧结与性能[J]. 东北大学学报(自然科学版), 2010, 31(1):56-59.

[17] 杜贤武. 聚碳硅烷及氧化锆对B4C热压致密化、结构及性能的影响[D]. 武汉：武汉理工大学, 2015.

[18] 穆柏春, 唐立丹, 张辉,等. Y2O3和La2O3对B4C基陶瓷烧结致密化及其结构和性能的影响[J]. 特种铸造及有色合金, 2009, 29(10):886-889.

[19] 刘琳.改性聚甲基硅烷系列SiC陶瓷先驱体的研究[D].长沙：国防科学技术大学，2008.

[20] EMIK C M, ZROLFGANG G. Precise nondestructive determination of density of porous ceramics[J]. Journal of the American Ceramic Society, 1989, 72(2)：1269-1270.

[21] 王零森,杨义斌,张金生,等.碳化硼烧结动力学和烧结机制[J].中南大学学报(自然科学版)，1999(5):505-508.

[22] 王零森,杨义斌.掺碳碳化硼活化烧结及其动力学[J].中国有色金属学报， 2000,10(1):37-42.

[23] HUANG Y H, JIANG D L, ZHANG J X,etal. Sintering kinetics of YAG ceramics[J]. Journal of Rare Earths, 2014, 32(5):416-422.

[24] 巴春秋. 硅酸铝锂组成的玻璃陶瓷烧结和结晶机理的研究[J]. 耐火与石灰，2004,29(5):50-53.

[25] 黄培云. 粉末冶金原理[M].北京: 冶金工业出版社,1981:251-274.