数学表达:学生数学核心素养发展的实践范式
2018-01-18席爱勇
席爱勇
摘要:数学表达是学生数学核心素养发展的重要的实践范式。数学表达可以改善学生的数学学习生态、教师的数学教学生态、课堂的教学相长生态和课程的动态发展生态,通过动作表达、口语表达和书面表达,帮助学生不断建构对数学知识的理解,强化数学技能的掌握,呈现数学观察、实验、猜想、运算、推理、验证等思维过程以及数学问题解决的思路方案,让学生的数学核心素养落地生根。
关键词:数学表达;实践范式;数学核心素养
中图分类号:623.5 文献标志码:A 文章编号:1673-9094(2017)11B-0020-04
当前,数学教育已聚焦于发展学生数学核心素养,让学生逐步学会用数学的眼光观察世界,用数学的思维分析世界,用数学的语言表达世界。如何让这样的数学教育目标落地生根,已成为一线教师思考和探索的热门话题。在教学实践中,笔者尝试以数学表达为突破口,着力于探索发展学生数学核心素养的实践范式。
一、数学表达的内涵和价值
所谓数学表达,就是用动作、口语或书面(图像、符号、文字等)的形式描述展示数学知识技能、思维过程、思想方法、问题解决等的一种行为。数学表达以数学交流和传播为目的,以数量关系和空间形式为内容,以数学语言(图像语言、符号语言、文字语言)为工具,以动作、口语、神情或书写为媒介。
数学表达是学生数学学习的重要环节。通过数学表达,可以帮助学生不断建构数学知识的理解,强化数学技能的掌握,呈现数学观察、实验、猜想、运算、推理、验证等思维过程以及数学问题解决的思路方案,是聚焦学生数学核心素养发展的有效实践范式。
数学表达,可以改善学生的数学学习生态,让学生从被动的听讲、做题、订正、大量做题,到主动的观察、操作、思维、表达、交流与反思,把数学学习从知识技能训练上升到数学文化交流的层面。这个过程有助于学生自我反思、自我完善、自我评价和自我提升,在比较轻松的环境氛围中深刻理解数学知识,灵活掌握数学技能,不断提升数学思维能力和品质,提高数学表达和交流能力。
数学表达,可以改善教师的数学教学生态,让教师从繁重琐碎的讲解、练习、批改和辅导中解脱出来,更具智慧地倾听、点拨、激励和指导,真正地以学生为主体。这个过程有助于教师更多地从学生视角思考教学,及时把握学生的思维状态、生成状态,及时了解学生,读懂学生,研究学生,及时采取有效措施进行有针对性的教学,锤炼更灵活的动态调整和即时应答的教学智慧,有利于促进学生数学核心素养的更好发展。
数学表达,可以改善课堂的教学相长生态。数学课堂是师生积极参与、交往互动、共同发展的教学相长的重要载体,通过重建“数学问题情境—个体尝试性表达—集体完善性表达—实践应用性表达—总结拓展性表达”的数学表达课堂,可以让数学课堂更具智慧生成性和互动发展性。
数学表达,可以改善课程的动态发展生态,让数学课程从国家规定、教材编定、师生执行的固定不变状态,变成师生共同开发、不断进行资源整合的多元化动态发展状态,为促进学生数学核心素养的发展搭建更有利的平台。
二、数学表达的实践策略
(一)动作表达:在直观中发展学生的数学核心素养
动作表達,可以通过运动、动手操作或数学实验,积累感性经验,发展学生直观想象能力,融通感性和理性的通道,达到认识和理解数学的目的,让学生有一种豁然开朗的感觉。
1.动作演示,直观认识数学
在数学教学中,教师可以有意识地将数学书面表达的内容转换成动作表达,转换成生动有趣的动作表演或演示,让学生在积极体验中认识和理解数学。
例如在《平移和旋转》的教学中,学生在观察生活中的平移和旋转现象后不仅要学会用口语来描述,还应该学会用手势来表达平移和旋转现象。在《认识方向》的教学中,笔者让学生来到学校操场,站立,面向早晨冉冉升起的太阳,一边做动作操一边说:“前面是东,后面是西,左面是北,右面是南。”然后随意变换方向,让学生继续边做动作操边说。学生在轻松愉悦的自编自做的动作操中认识了生活中的东南西北,理解了东南西北方向的稳定性和前后左右的相对性。
2.数学实验,直观理解数学
学生受认知水平的限制,在一定年龄阶段很难从理性上深刻认识和理解某些数学知识,通过数学实验,从感性层面让学生进行直观的认识和理解可能会更好。例如,让小学六年级学生从理性层面理解“在周长一定的情况下,圆的面积最大”比较困难,这时就可以做一个数学实验。让学生用同一根绳子先后围成一个三角形、一个长方形、一个正方形、一个五边形、一个六边形、一个圆形,学生一边围一边观察,就会直观感受到围的面积越来越大,围成圆后,再也无法围成面积更大的图形了,较轻松地理解了“在周长一定的情况下,圆的面积最大。”再如,利用天平做数学实验可以让学生直观理解1千克铁和1千克棉花一样重。在天平左边放1千克铁,在天平右边放1千克棉花,观察天平是否仍然保持平衡。类似的,还可以利用天平做数学实验,引领学生直观理解等式的性质,天平平衡后在两边加入或拿走同样重的砝码,观察天平是否仍然保持平衡,从而直观理解等式的性质:在等式的两边同时加上或减去同一个数,结果仍然是等式。
(二)口语表达:在言说中发展学生的数学核心素养
让学生讲给别人听,往往比听别人讲更高效,学生能言说到什么程度,常常说明了他们的理解程度。因此,让学生用口语来表达对数学的认识和理解,是重要的数学学习方法和策略。
1.动作口语化表达
在《轴对称图形》的教学中,笔者让学生先观察生活中的对称现象,折线两边一模一样,然后把轴对称图形进行对折,在动手操作中发现折线两边都能完全重合。这时,最好让学生用口语把操作过程表达出来:“通过对折,折线两边能够完全重合,这样的图形就是轴对称图形。”
2.图像口语化表达endprint
在《认识方程》的教学中,笔者让学生看图1进行说话,把每一幅图的意思用口语表达出来:第1幅图表示在天平的左边放了x克正方体木块和50克砝码,在天平的右边放了100克砝码,发现天平向左边倾斜,说明x克正方体木块和50克砝码的和,比100克砝码重。第二幅图表示把天平右边的100克砝码换成200克砝码,结果发现天平向右边倾斜,说明x克正方体木块和50克砝码的和,比100克砝码轻。第三幅图表示把天平右边的200克砝码换成100克砝码和50克砝码,结果发现天平平衡了,说明x克正方体木块和50克砝码的和,与右边150克砝码一样重。学生能用口语表达出来下面三幅图的意思,说明初步看懂并认识了不等式和等式的本质。在此基础上,教师引导学生分别用式子表示出三幅图表达的意思,学生就能很快写出:x+50>100,x+50<200,x+50=150。
3.符号口语化表达
数学教材中很多符号表达式需要通过口语化表达来解读,才能被更多学生所理解和接受。在数学教学中,教师要适时引导学生对教材中的数学符号表达式进行解读,让他们明白蕴含其中的本质内涵。例如,s=vt表示“路程=速度×时间”,还表示“路程一定,速度和时间成反比;速度一定,路程和时间成正比;时间一定,路程和速度成正比。”a+b=b+a表示加法交换律,即“交换两个加数的位置,和不变。”
(三)书面表达:在表征中发展学生的数学核心素养
教学实践中,引导学生把生活现象数学化,用图像、符号或文字表达出来,有助于学生在多元表征中认识、理解和应用数学。
1.图像表达,在直观表征中发展学生的数学核心素养
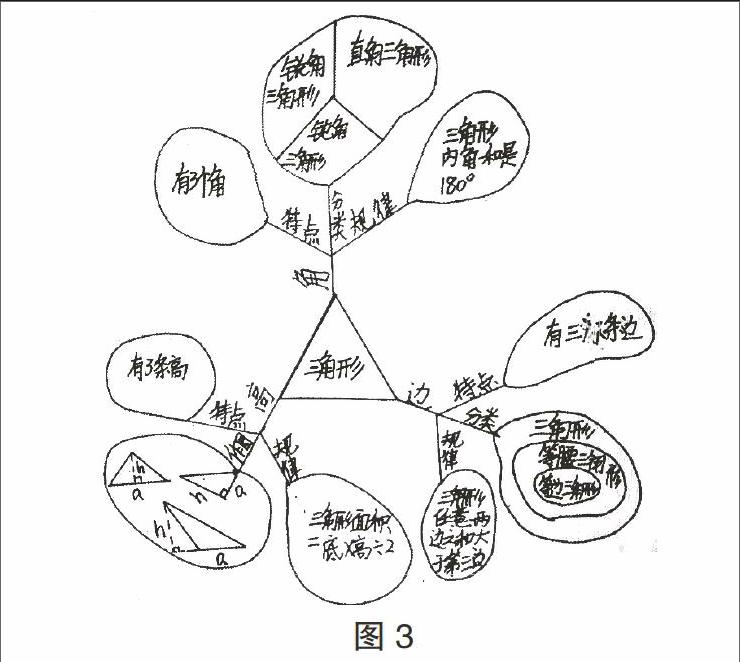
用图像表达可以把抽象的数学直观形象化,易于理解和掌握。这里的图像既可以是实物图,也可以是示意图、统计图、流程图、网络结构图或思维导图等等。我们可以根据实际需要,灵活选择合适的表达方式,如算理可以选择实物图或示意图表达。图2即是用实物图和计数器两种图像表示45+3。
我们还可以选择网络结构图对数学知识实现连点成线,连线成面,连面成体。在这个过程中,学生的数学思维逐步从零散走向联系,从碎片走向系统,从而打通数学知识的内在联系,实现系统化建构,便于他们在以后相关的数学学习和生活实践中灵活提取和综合应用。
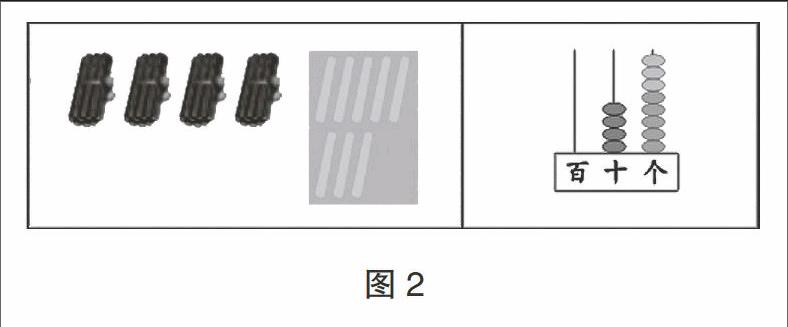
例如,学生学完“三角形”以后,笔者引导他们作一些梳理。图3可以清晰看出,学生从三角形的角、边、高三个纬度出发,每一个纬度又可分成“特点、规律、分类、作图” 等多个方面,多维度、网络化、立体式建构三角形的知识结构体系。学生以后再学习三角形的相关知识(如初中学习全等三角形和相似三角形、三角函数等)也会自然从这些纬度进行数学思维,不断充实完善三角形的知识结构体系。同时,学生在遇到三角形方面的实际问题时,也会自然从这些纬度灵活提取相关数学知识,综合运用相关数学知识分析解决实际问题。可见,图3不仅仅是三角形知识结构的全面整理,更是学生对三角形全面再认识的数学思维的系统整理。
2.符号表达,在符号表征中发展学生的数学核心素养
数学是一个符号系统,符号既是数学的语言,也是数学的工具,更是数学的方法。符号的认识和使用贯穿于学生数学学习的始终,学生从认识数学符号开始,经历表征数学符号的意义和结构,使用数学符号解决数学和生活实际问题,建构数学模型,进行数学思考和表达交流,形成数学符号意识的过程。
用符号表达可以分为三个阶段。
第一阶段:符号认知阶段。具体表现为能认识符号,理解符号所表示的数学含义和结构;能使用符号表示数、数量关系和变化规律,建构数学模型;能解释符号所表示的数学含义和结构。
义务教育阶段,学生需要认识和理解的数学符号主要有:(1)数字符号:0、1、2、3、4、5、6、7、8、9。(2)字母符号:S(面积)、h(高)、s(路程)、v(速度)t(时间)等等。(3)关系符号:>、<、=、≈、≠、≥、≤、⊥、∥、≌、∽等等。(4)运算符号:+、-、×、÷ 等等。(5)分类符号:( )、[ ]、{ }等等。(6)单位符号:km、m、dm、cm、mm、㎡、t、kg、g、℃、%等等。(7)定义符号:∠1、△ABC、∣-3∣、(1,2)等等。
每种数学符号都有它特定的数学含义、使用规则和结构特点,学生首先要逐步认识各种类型的数学符号,理解并能解释各种数学符号所表示的数学含义,符号与符号之间的内在联系,符号的使用规则和结构特点,为正确使用符号做好准备。使用符号表示数,这里的数,既可以是某个未知数,也可以是某个区间内的数,还可以是不断变化的数;用符号表示数量关系和变化规律,可以是代数式、方程、不等式,也可以是数学公式、函数关系式等数学模型。
符号表征不仅表现在能正确认识、理解和使用数学符号,还表现在能正确解释符号所表示的数学含义和结构。如x在方程中表示未知数,在函数中则表示自变量;(4,6)既可以表示点的坐标,也可以表示求4和6的最大公因数;a+b=b+a表示加法交换律等等。学生要能够根据数学背景正确解释符号所表示的数学含义和结构。
第二阶段:符号操作阶段。具体表现为掌握符号的使用规则和操作程序,使用符号进行形式运算和推理,作出判断,知道得到的结论具有一般性。如根据等式的性质解方程或进行公式变形等等。使用符号进行数学证明的过程,就是一个推理过程,最简单的如a>b,b>c,则a>c。
第三阶段:符号思维阶段。具体表现为能自觉主动、自动化使用符号和表达式进行思考和交流,把符号作为发现和解决问题的工具,用“代数”的眼光看待社會生活现象,进行综合实践与创新,形成符号的思维方式和表达交流意识。
3.文字表达,在文字表征中发展学生的数学核心素养
数学要通过对数量和数量关系、图形和图形关系的抽象而抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并且用数学符号或者数学术语予以表征,形成数学概念、命题、结构和系统。因此,学生能够科学规范地使用数学术语,表达数与代数、图形与几何、概率与统计等领域的数学内容,是数学核心素养高的重要标志。endprint
4.綜合表达,在多元表征中发展学生的数学核心素养
综合运用图像、符号、文字进行多元化灵活性的数学表达,有利于帮助学生实现各种表达方式之间的灵活转换,逐步学会根据实际情况和需要选择运用合适的表达方式,发展学生开放灵活的综合性思维。
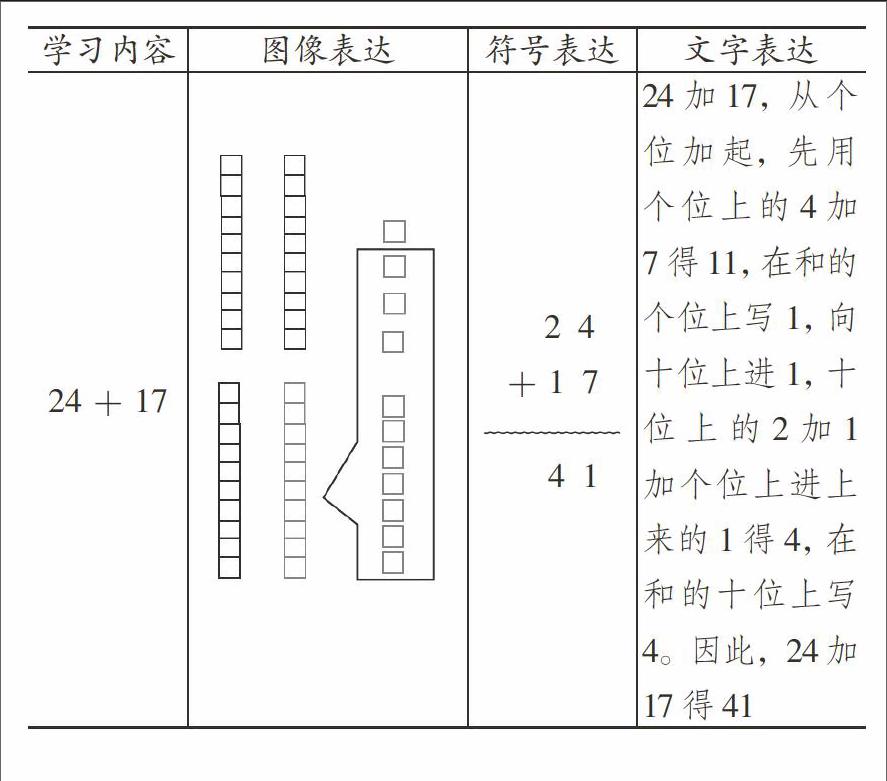
例如24+18的计算过程可以用三种表征方式,表达如下:
数学表达,从内容层面,聚焦于数学运算、直观想象和数据分析;从思想层面,聚焦于数学抽象、逻辑推理和数学模型;从文化层面,聚焦于数学作为科学语言的文化交流和推动人类社会发展进步的功能。数学表达,真正让学生的数学核心素养落地生根。
责任编辑:宣丽华
Abstract: Mathematics expression is an important practical paradigm for the development of students mathematics core accomplishments, and it can improve students learning ecology, teachers teaching ecology, classroom teaching ecology and curriculum dynamic developmental ecology. Action, oral and written expressions can help students constantly construct their understanding of mathematics knowledge and reinforce their mastery of mathematics skills. Meanwhile, presentation of such thinking process as mathematics observation, experiment, guess, operation, reasoning and testing can help them form and develop their mathematics core accomplishments.
Key words: mathematics expression; practical paradigm; mathematics core accomplishmentendprint
