移相全桥DC/DC变换器分数阶PIλDµ控制的研究

任旭亮，易灵芝,2，陈 宇，李青平，朱和潇

（1.湘潭大学 信息工程学院，湘潭 411105；2.湖南省“风电装备与电能变换”2011协同创新中心，湘潭 411101）

0 引言

近年来，移相全桥DC-DC变换器损耗小，效率高且可以实现软开关，在中大功率场合应用广泛。由于存在非线性特征，传统整数阶PID控制方式在快速性、稳定性和抗干扰性均难以达到某些场合的特殊要求。相对于传统整数阶PID，智能控制虽然性能较好，但在实际应用中难以实现。分数阶理论的发展，为解决这种问题提供了可行性，可用来提高变换器控制效果[1,2]。

基于传统PID控制器，I.Podlubny教授提出分数阶PID控制[3]。分数阶PID控制是对传统整数阶的概括和补充，相比传统PID多了两个可调参数积分阶次λ和微分阶次µ，PIλDµ控制器的参数整定范围变大，其控制更加灵活，使系统具有更好的鲁棒性和控制效果[4]。本文以移相全桥DC-DC变换器为对象设计其分数阶控制器与整数阶比较，提高稳定性和抗干扰能力。

1 移相全桥变换器建模

移相全桥变换器拓扑如图1所示，开关管Q1和Q3组成超前桥臂，Q2和Q4组成滞后桥臂。通过调节前后桥臂导通角之间的相位差（即移相角），来调节输出电压的大小。文献[5]以Buck变换器作为移相全桥变换器为基础，考虑两者之间明显区别，即移相全桥变换器谐振电感Lr与开关管并联电容产生谐振，使开关管工作于软开关状态时造成占空比丢失。在移相全桥变换器中，变压器副边有效占空比不仅与原边占空比d相关，还与输出电感电流IL，谐振电感Lr，输入电压Vin和开关频率fs有关。将以上影响加到图2所示的Buck电路小信号等效模型中。

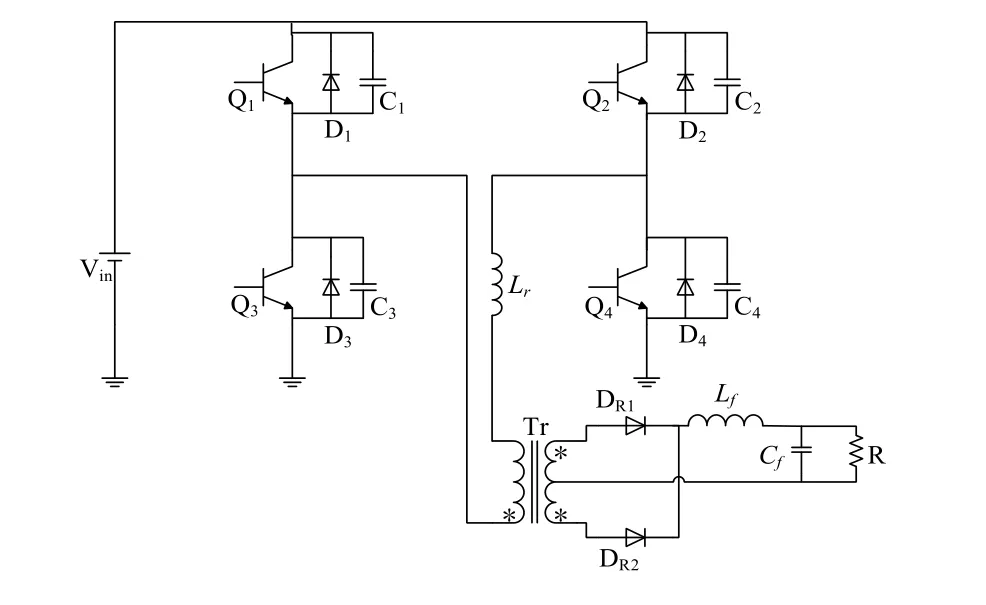
图1 移相全桥变换器电路拓扑

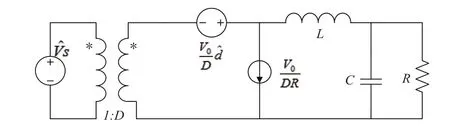
图2 Buck电路小信号等效模型

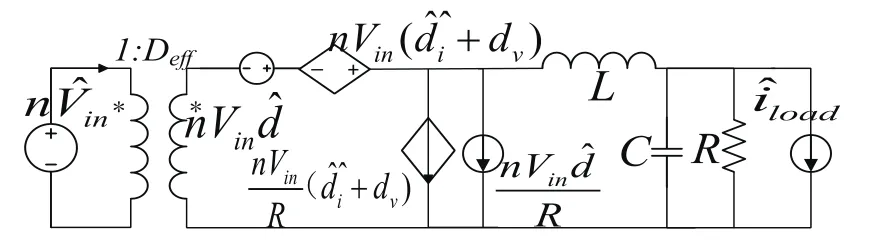
图3 移相全桥变换器小信号模型

用Deff替换替换占空比扰动，且代替直流输入电压扰动得到图3所示的移相全桥变换器的小信号模型。由图3，得到移相全桥DC-DC变换器传递函数，即：

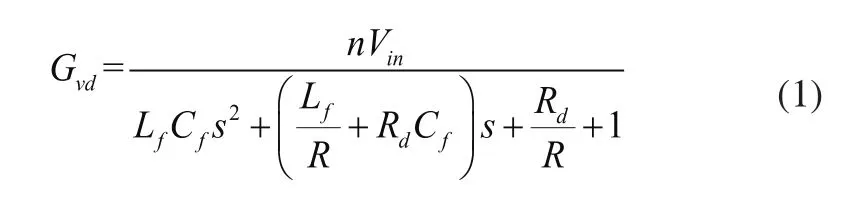
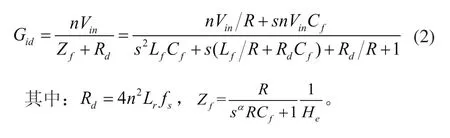
2 分数阶微积分控制器

2.1 分数阶微积分（FOPID）

在分数阶微积分的发展历程中，不同的领域，分数阶微积分的定义是不完全相同的。在控制领域，常用的定义有Grünwald-Letnikov(GL)、Riemann-Liouville(RL)和Caputo定义[6,7]。不同的定义应用范围、特点和优势均不同。Caputo定义的分数阶微分在其初始条件的导数为0，具有明确的物理意义，其Laplace变换在控制领域应用广泛[8]。

Caputo分数阶定义如式(3)所示：

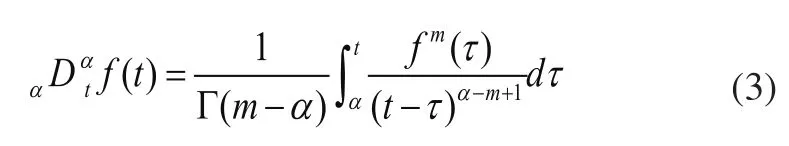
式(3)中：Г为伽马函数，m-1＜ɑ＜m，m取整数。

对式(3)表示的Caputo分数阶微积分函数进行Laplace变换为：

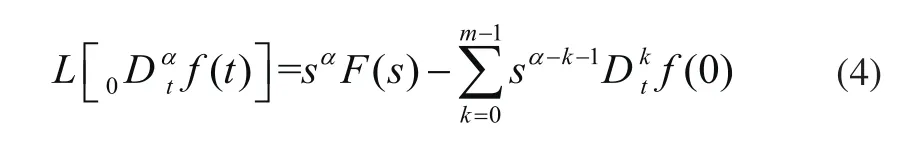
其中：n−1≤α≤n，α∈N。

式(4)在零初始条件下，其求和项为零，因此得到分数阶PIλDµ控制器传递函数为：

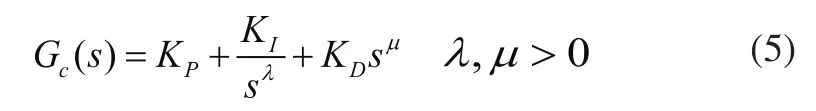
其中，λ为积分阶数，μ为微分阶数。

2.2 分数阶PIλDµ控制器数字实现

由于分数阶控制系统的传递函数是无限维的，实际中难以实现。因此需要对分数阶控制系统进行有理化的近似。分数阶PIλDµ控制器离散化方法主要有直接离散化方法和间接离散化方法。通过采用Oustaloup间接近似化方法[9]，来近似实现分数阶PIλDµ控制器。假设给定频段建立连续的滤波器传递函数为：

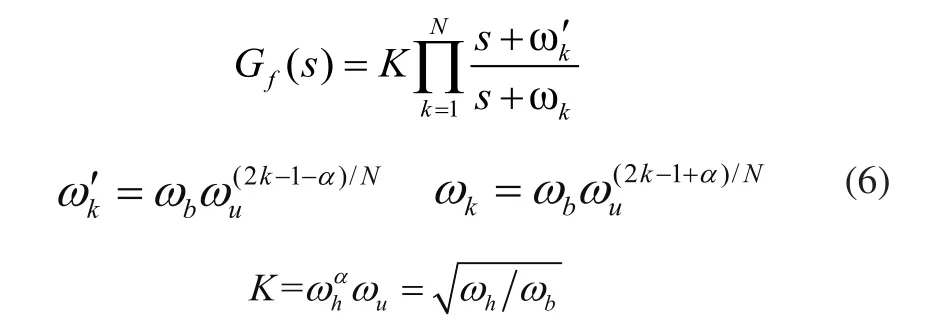
2.3 分数阶PIλDµ控制器设计

分数阶PIλDµ控制器可以对KP，KI，KD，λ，μ这个5个参数调整，引入了积分阶次λ和微分阶次μ使得系统的鲁棒性，稳定性和整体的控制性能等方面提高，其控制结构框图如图4所示。由于分数阶PIλDµ控制器需要对5个参数调整，在参数优化上比传统PID困难。

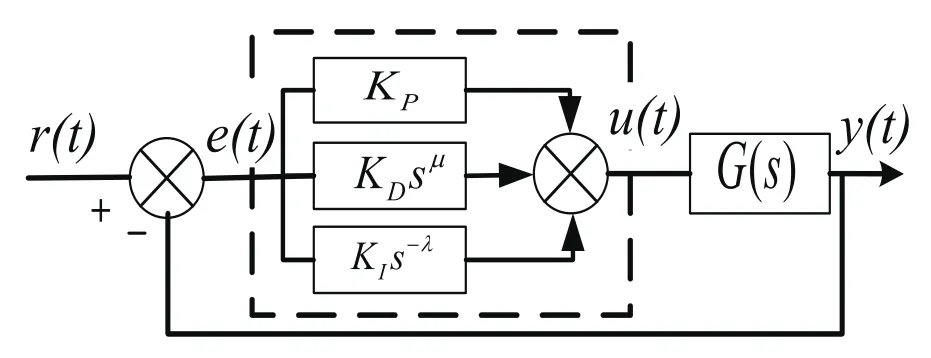
图4 分数阶PIλDµ控制框图

因此，本文采用粒子群优化算法（PSO），从而快速有效的调整分数阶PIλDµ控制器参数，为了满足系统动态特性，以ITAE作为性能指标，定义如下：

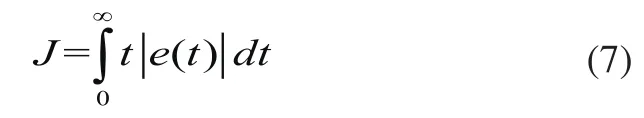
其中，t为时间，e(t)表示误差。

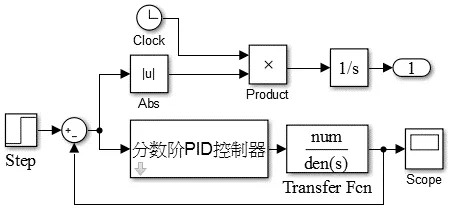
图5 以ITAE为指标的分数阶参数整定Simulink框图

如图5所示，根据Oustaloup滤波算法在Simulink中建立的分数阶微积分仿真模块，对式(1)移相全桥DC-DC变换器分数阶传递函数，基于PSO算法进行参数整定。经过参数寻优，得到相关的控制器参数KP，KI，KD，λ和μ。

3 实验验证

3.1 仿真实验

为了验证移相全桥变换器分数阶控制方法的控制效果，分别基于分数阶PIλDµ控制和传统整数阶PID控制方法下进行仿真实验。移相全桥DC-DC变换器主电路参数如表1所示。

基于图5所示的仿真模型，将表1参数代入式(1)的传递函数，基于粒子群算法以ITAE指标对其进行参数优化。设种群维数为50，最大迭代次数为50，惯性因子w为0.6，加速度常数c1=2，c2=2，粒子最小适应值为0.1。在λ=0.75，μ=0.5，分数阶PIλDµ参数优化曲线如图6所示。

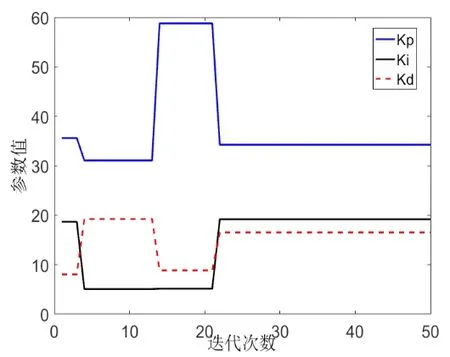
图6 分数阶PIλDµ参数优化曲线

由图6得到优化后的分数阶PIλDµ控制函数为：

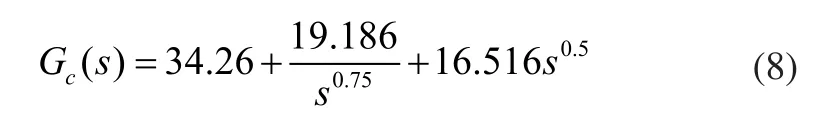
在相同条件下，PSO算法优化后的整数阶PID优化曲线如图7所示。

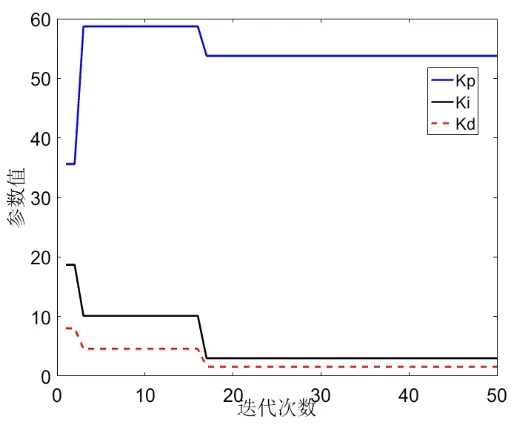
图7 整数阶PID参数优化曲线

由图7得到优化后的整数阶PID控制函数为：

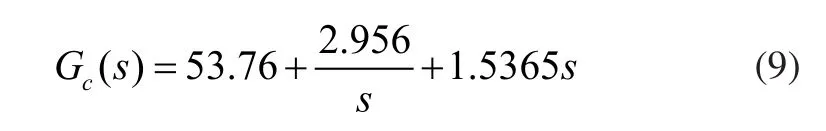
优化后分数阶PIλDµ控制器和整数阶PID控制器的单位阶跃响应曲线，如图8所示。

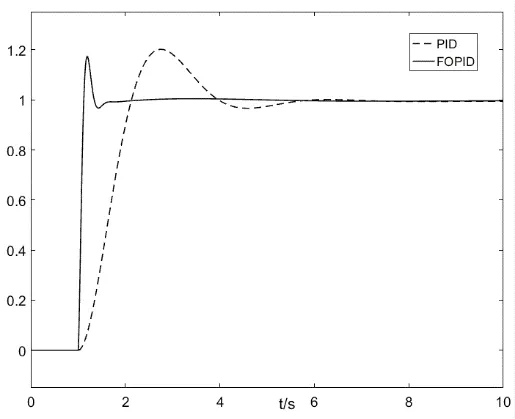
图8 FOPID与PID控制阶跃响应

由图8可以看出：相比传统整数阶PID控制器，移相全桥DC-DC变换器分数阶PIλDµ控制器快速性更优、调节时间更短、且能更快趋于稳态。

根据图1的移相全桥变换器电路拓扑和表1的仿真参数，基于Simulink平台搭建仿真模型。其他条件保持不变，分别以式(9)的传统PID函数与式(8)的分数阶PIλDµ函数进行闭环仿真实验。

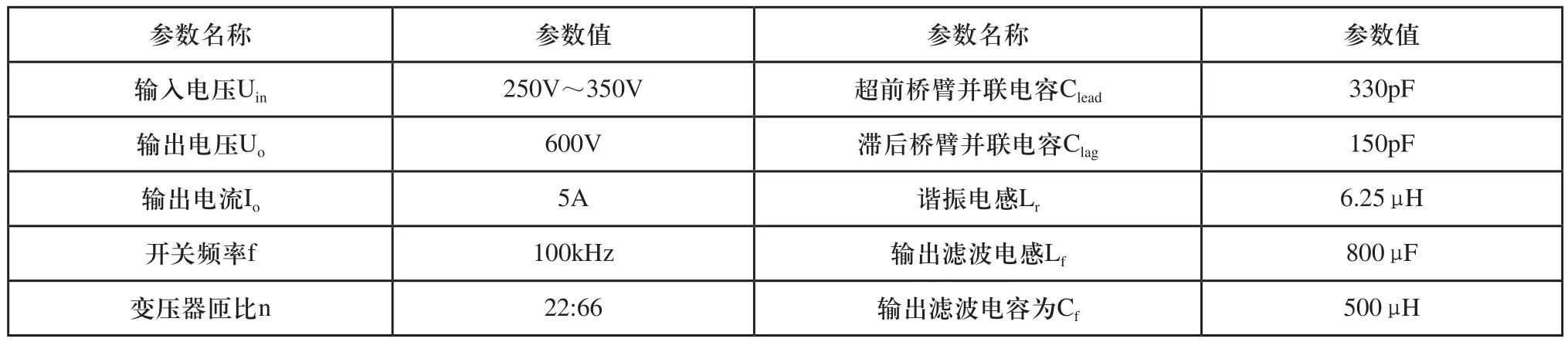
表1 移相全桥变换器主电路仿真参数

当负载由120Ω跳变为300Ω时，整数阶PID控制方式与分数阶PIλDµ控制方式下输出电压Uo和负载电流Io波形如图9与图10所示。

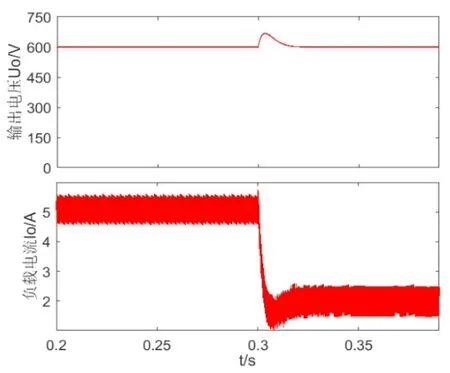
图9 整数阶PID负载变化瞬态响应

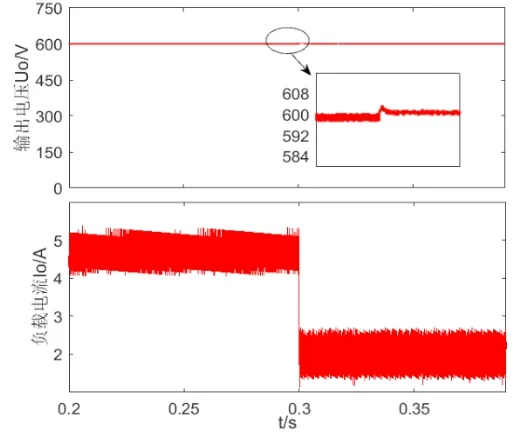
图10 分数阶PIλDµ负载变化瞬态响应

当负载在0.3s变化时，使用整数阶PID控制时，输出电压过冲约为70V，调节时间约25ms。分数阶PIλDµ控制方式下，输出电压过冲不到10V，调节时间约5ms。

因此对比可知，分数阶PIλDµ的控制器比整数阶PID电业恢复快，过冲小。

3.2 样机实验

本文采用TMS320F28335PTPQ作为主控制器在实验室搭建3kW的移相全桥DC-DC变换器实验样机。变压器原边主开关管MOSFET采用SPW47N60C3，副边整流二极管采用DESC30-12A。如图11所示。

在实验中，分数阶PIλDµ控制器采用直接离散化方法Tustin+CFE的方法对分数阶微积分算子进行有理化[10]。对式(8)中微积分算子有理化，积分算子1/s0.75与微分算子s0.5的有理近似表达式：

图11 3kW移相全桥DC-DC变换器样机

样机参数与表1一致，波形如图12与图13所示。

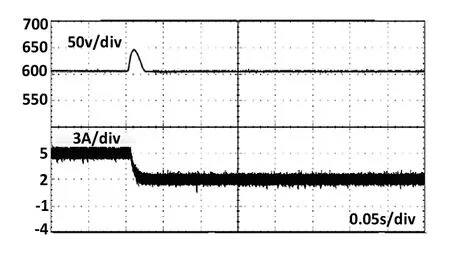
图12 整数阶PID控制下负载变化输出电压电流

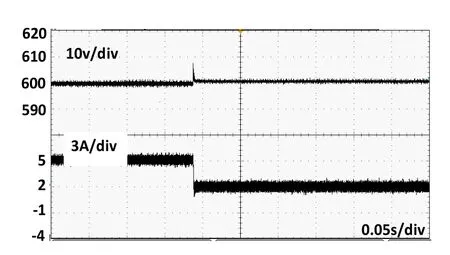
图13 分数阶PIλDµ控制下负载变化输出电压电

由图12与图13波形对比可知，样机实验结果与仿真波形基本保持一致。采用分数阶PIλDµ控制方式的移相全桥变换器，当负载发生变化时，副边输出直流电压上冲幅度小，动态调节时间短和更强的鲁棒性。硬件实验结果与仿真基本一致。

4 结论

将分数阶PIλDµ控制器应用在移相全桥变换器中代替传统的PID控制器，基于粒子群优化算法对分数阶PIλDµ和传统PID控制器进行参数整定。通过仿真和样机实验结果对比分析，表明了对于移相全桥DC-DC变换器，分数阶PIλDµ控制器优于传统PID控制器，提高系统的动态性能和使系统具有更强的稳定性。

[1]Rabia Nazir, Keliang Zhou, Neville Watson, Alan Wood.Analysis and synthesis of fractional order repetitive control for power converters[J].Electric Power Systems Research,2015,124(7):110-119.

[2]Swapnil Khubalkar, Amit Chopade,Anjali Junghare.Design and Realization of Stand-Alone Digital Fractional Order PID Controlle[J].Circuits Systems and Signal Process,2016,35(6):2189-2211.

[3]I.Podlubny. Fractional-order systems and PIλDµcontrollers[J].IEEE Transactions on Automatic Control,1999,44(1):208-214.

[4]D.Zhu, L. Liu and C. Liu.Optimal fractional-order PID control of chaos in the fractional-order BUCK converter[A].2014 9th IEEE Conference on Industrial Electronics and Applications,Hangzhou[C].2014:787-791.

[5]V. Vlatkovic, J. A.Sabate, R. B. Ridley, F. C. Lee and B. H. Cho.Small-signal analysis of the phase-shifted PWM converter[J].IEEE Transactions on Power Electronics,1992,7(1):128-135.

[6]赵春娜,李英顺,陆涛.分数阶系统分析与设计[M].北京:国防工业出版社,2011.

[7]OSHI S D, TALANGE D B. Integer& Fractional Order PID Controller for Fractional Order Subsystems of UAV[A].2013 IEEE Symposium on Industrial Electronics and Applications[C].2013:21-26.

[8]马霄.分数阶PID控制器数字实现及应用研究[D].河北大学,2014.

[9]OUSTALOUP A, LEVRON F, MATHIEU B, et al. Frequency band complex no integer differentiator. Characterization and synthesis[J].IEEE Transactions on Circuit and Systems-I:Fundamental Theory and Applications,2000,47(1):25-39.

[10]赵慧敏.分数阶控制器数字实现方法及其振动抑制性能研究[D].大连交通大学,2013:26-28.