基于Scheimpflug定律的线结构光系统摄像机标定方法
2018-01-18
(华中科技大学 机械科学与工程学院国家数控系统工程技术研究中心,武汉 430000)
0 引言
在光电检测领域,激光三角法以其快速、非接触、高精度的特点,被广泛使用,其中市场上出现最多的是基于线结构光的激光三角测量系统,已经有相应的产品,如北京大恒公司代理国外厂商LMI Technologies INC的Gocator智能传感器系列产品,通过投射线结构光达到测距、测截面轮廓等目的。线结构光三维测量系统的标定是获取三维信息的关键步骤,有许多学者都对其进行了研究,但是多数都不是恒聚焦光路,对摄像机的标定采用传统的线性模型与非线性模型,有如学者周富强、张广军[1],提出了一种新的基于自由移动平面参照物的表面视觉传感器全部参数的高精度简易标定方法;学者陈新禹等[2]提出的提出了一种基于单一圆形标靶标定线结构光视觉传感器的方法,他们的系统都是基于摄像机和透镜平行放置来建立的。
本文以线结构光三维测量系统为支撑,为达到高精度测量,设计了满足恒聚焦光路条件的硬件系统,由于光路条件的改变,原有的摄像机标定的线性模型以及非线性模型不足以描述本系统摄像机模型,因此本文深入研究了恒聚焦光路的数学模型,并建立了基于倾斜镜头的摄像机标定模型。
1 线结构光系统恒聚焦光路
线结构光传感器原理如图1所示,线激光照射到被测物表面,激光在表面上会发生漫反射,反射的光线由光学透镜汇聚在光敏接收单元上,如果被测表面有位移变化,通过检测光敏单元上激光位置变化,就能得到物体位移的变化,这就是激光三角法的测量原理。传统的三角测量过程都保证透镜主平面与成像元件光敏面平行,一旦系统调试好,准确聚焦的位置只有一个,其余都处于离焦状态,为使被测表面上任一点都能在透镜上清晰成像,提高系统检测精度,系统需要满足Scheimpflug定律,也称沙姆定律,该定律物理意义上描述为激光轴线光束、成像透镜主平面、光敏单元三者延长线必须相交与一点[3]。为此,光敏单元相对于透镜必须有一个夹角。该定律的证明如下:

图1 线结构光传感器原理

图2 恒聚焦光路图
图2中,α是激光轴线与透镜光轴的夹角;β是感光元件平面与光轴的夹角;物点A在感光面上的像点是A'点,a是该点的物距,b是该点像距;同理B点。ρ是BB'与光轴之间的夹角;f是透镜的焦距。已知透镜成像公式:
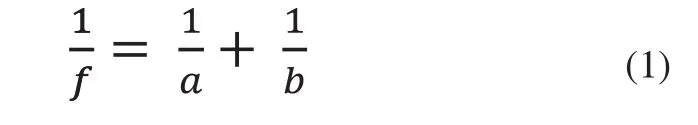
只要满足公式(1)的都可以在光敏元件上清晰成像,为此当物点从A移到B点时,也要满足清晰成像公式,即:


联立式(1)~式(3)得:

式(4)是沙姆定律的数学表达式。即为保证成像系统满足Scheimpflug定律,透镜与光敏单元之间的夹角必须存在。由此满足恒聚焦光路条件的摄像机系统中镜头是倾斜的。
2 倾斜镜头摄像机模型建立
倾斜镜头摄像机模型是建立在摄像机线性模型和非线性模型基础之上的。
2.1 摄像机线性模型
摄像机的线性模型是一种理想的模型,又可称作针孔模型[4]。是在透视投影基础上加上刚体变换(刚体的旋转与平移)得到的摄像机模型[5]。为了了解线性模型,先要了解几个常用坐标系之间的变换关系,建立的坐标系如图3所示。

图3 摄像机常用坐标系
摄像机常用坐标系主要有图像坐标系O0uv,成像平面坐标系O1xy,摄像机坐标系OcXcYcZc以及世界坐标系OwXwYwZw,其中图像坐标系建立在图像平面内,原点在图像的左上角,以像素单位为量纲。成像平面坐标系建立在CMOS平面内,原点建立在光轴与CMOS平面的交点位置上,一般为中心,成像平面坐标属于物理坐标系。摄像机坐标系建立在摄像机上,坐标原点OC与透镜中心重合,ZC轴与光轴重合,XC和YC轴分别与成像平面坐标系的x轴和y轴平行,如图3所示,对于理想的针孔模型,要求物点P、光心OC和像点p这三点须在同一直线上[6]。
为了建立各个坐标系之间的关系,假设成像坐标系原点O1在图像坐标系中的坐标为(u0,v0),每个像素在x方向的实际物理尺寸设为SX,在y方向的物理尺寸记为Sy,量纲为mm,镜头焦距设为f,在图像坐标系中取点(u,v),可得图像坐标系与成像坐标系之间的变化关系式:
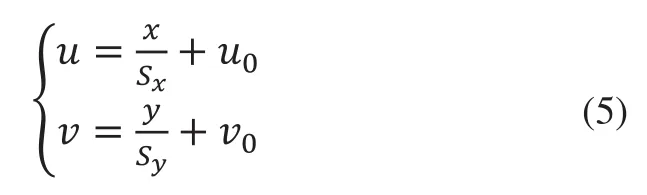
用齐次坐标表示为:
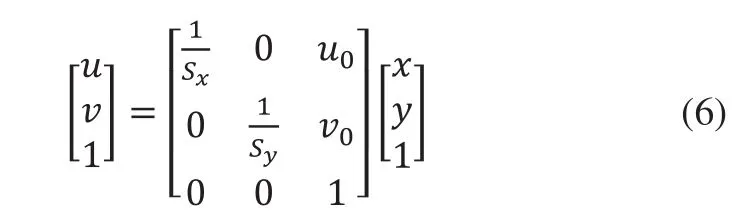
成像平面坐标系中的点(x,y)与摄像机坐标系中的点(Xc,Yc,Zc)之间的关系为:

同理写成齐次坐标形式为:

摄像机坐标系中的点(Xc,Yc,Zc)与世界坐标系中的点(Xw,Yw,Zw)变换属于空间坐标坐标变换范畴,变换关系为:

式(3)~式(9)中,R是旋转矩阵,表示相机坐标系在世界坐标系中的方向矢量,T为三维平移向量,T=[Tx,Ty,Tz]T。
综上,从图像坐标系到世界坐标系之间的齐次变换为:
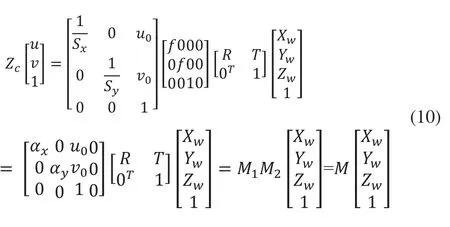
式(10)中,αx=f/Sx,αy=f/Sy,αx、αy、u0、v0只与摄像机内部参数有关,因此M1称为摄像机内部参数矩阵,而M2表征摄像机坐标系与世界坐标系的齐次变换,称之为摄像机外部参数,M=M1.M2,它表示了图像坐标系中的点与世界坐标系中点之间的关系,称之为投影矩阵。
2.2 摄像机畸变模型
采用理想的针孔模型,由于每次只有少量的光线通过针孔,这导致实际情况下曝光不足,图像生成很慢,摄像机为了快速生成图像,必须采用大面积而且弯曲的透镜,让足够的光线能够聚焦到投影点上,迅速生成图像,而这样做的代价就是引入了透镜的畸变[7]。透镜的畸变主要包含两方面,径向畸变与切向畸变。
径向畸变主要来自于透镜的形状,是由制造误差产生的。它的效应主要有两种:枕形失真和桶形失真,在CMOS中心(光学中心)的畸变为0,随着向边缘移动,畸变越来越严重。切向畸变来自于透镜安装的整个过程,因为安装时很难保证透镜和成像平面平行。
本文通过引入三个径向畸变参数k1,k2,k3和两个切向畸变参数p1,p2描述透镜畸变模型:
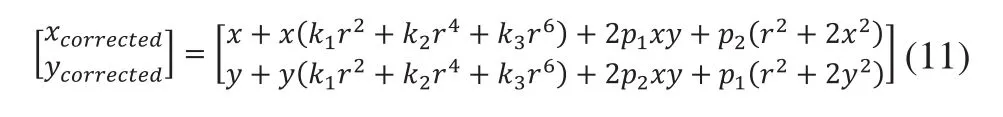
式(11)中(x,y)为实际成像坐标系中的点,(xcorrected,ycorrected)为校正之后的新位置。
2.3 倾斜透镜模型
为了使光学系统满足沙姆定律,透镜与光敏元件必须成一个夹角,因此要重新建立符合本系统的摄像机数学模型。
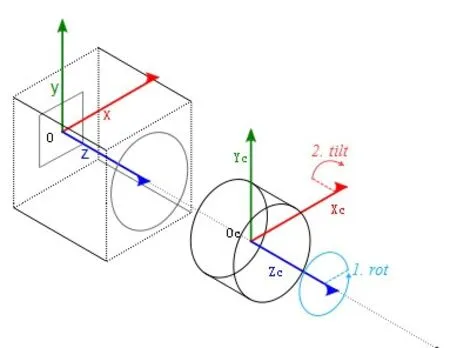
图4 倾斜透镜模型
如图4所示,为了描述CMOS相对于透镜倾斜的位置,在CMOS平面建立空间坐标系OXYZ,并引入两个旋转角度tilt和rot。tilt描述光轴相对于CMOS平面法线的倾斜角度,取值范围为[0,90°],在图中表示为YcOcZc绕x轴旋转角度的大小,也可以有其他的表示方式,这里只是描述角度大小的度量值。rot描述光轴倾斜的方向,取值范围为[0°,360°],在图中表示为ZC轴在XOY平面内的投影相对于X轴的旋转角度。从图像坐标系变换到世界坐标系的过程描述如下:

Step1:设在图像坐标系下一点的坐标为qi=(u,v)T,这时图像坐标系是建立在倾斜的CMOS面上的,映射到成像平面坐标系下的点为qt=(xt,yt)T,两者之间的变化关系如式(6)所示。
Step2:为了使用摄像机的线性模型求得最终世界坐标系下的坐标,必须将倾斜的成像平面上的点qt变换到与透镜平行的虚拟成像平面上的点去,它们之间的变换关系由透视变换(也称投影映射)描述:
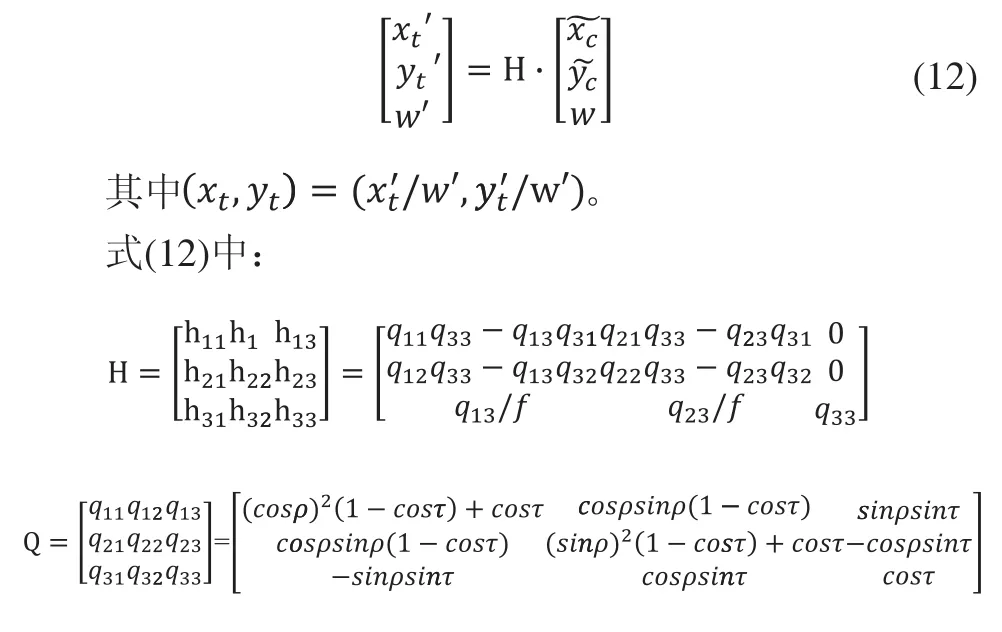
Step4:由理想的无失真的虚拟成像平面上的点qc变换到摄像坐标系下的点pc=(Xc,Yc,Zc)T,如式(8)所示。
Step5:由摄像坐标系下的点pc变换到世界坐标系下的点pw=(Xw,YwZw)T,如式(9)所示。
上述模型的建立,本文主要参考了HALCON机器视觉软件中对calibrate_cameras算子描述的英文文档,该模型为area_scan_tilt_polynomial(面扫描的多项式模型),有描述不当的地方可以查看原文。
倾斜镜头的摄像机模型的内部参数总共包含14个未知量:[f,k1,k2,k3,p1,p2,tilt,rot,Sx,Sy,Cx,Cy,ImageWidth,ImageHeight],其中Sx,Sy为像元尺寸,Cx,Cy是图像中心的坐标,也即(u0,v0)。标定的最终目的就是求出这14个未知量。
3 倾斜镜头摄像机的标定实验
本文使用标定辅助工具是德国MVTec公司开发的HALCON图像处理软件,其中有专门针对摄像机标定集成的一个标定助手,本文倾斜镜头模型的建立正是通过学习HALCON标定助手中area_scan_tilt_polynomial标定模型得到的。标定实验的硬件示意图如图5所示。
依据本系统的视野,选择HALCON30mm的标定板,结构如图6中所示,是一种包含黑色圆点的标定板。在系统满足了沙姆定律后,摄像机只能在激光所在的光平面附近清晰成像,在高度测量的方向上,反应在图像上就是一条清晰的光带。如图6所示,经观察,清晰成像区域大概在光平面前后3mm的范围内,因此使用标定板标定时,标定板只能放置在光平面附近,且前后改变姿态的位置不能超过3mm,否则无法清晰成像,提取不到标记点。
对于倾斜镜头模型的相机标定,HALCON也有一些特殊的说明:
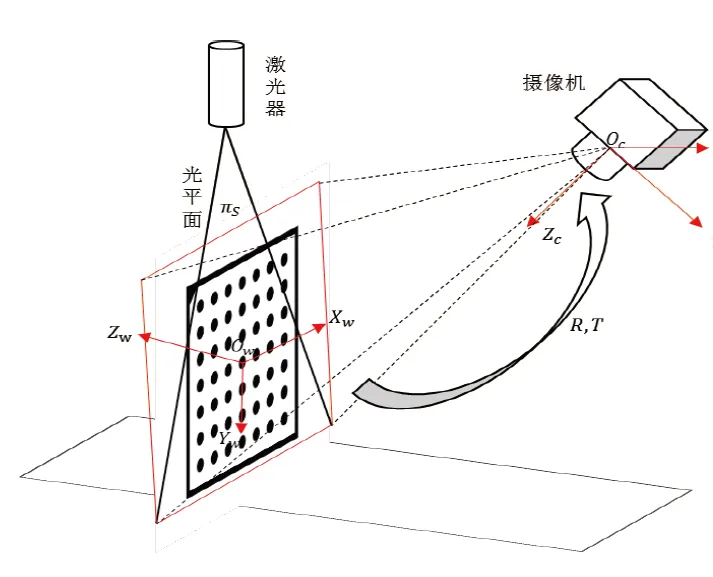
图5 标定实验的硬件结构图

图6 清晰光带

图7 标定图片
对于倾斜透镜,透镜失真越大,标定出的倾斜角度越准确。对于具有小失真的镜头,无法稳定地标定出倾斜角度,因此,标定出的角度可能与初始给定的角度显著不同,如果是这种情况,就要检查标定误差,如果误差小,则所得到的相机参数可用于精确测量。area_scan_tilt_polynomial模型的切向失真参数p1和p2在一定程度上能够对倾斜透镜进行建模。相反,倾斜参数能够在一定程度对p1和p2建模。因此,当使用多项式模型时,可能发生一些倾斜参数由p1和p2建模,另一些倾斜参数由tilt和rot建模。在这种情况下,所产生的倾斜参数可能会偏离初始设置的标准值。同样地,如果误差很小,优化得到的相机参数与实际参数一致性地描述了图像的几何成像,是可以使用的。如果使用area_scan_tilt_polynomial模型获取倾斜参数的实际值很重要,则应将参数p1和p2排除,即忽略切向畸变。
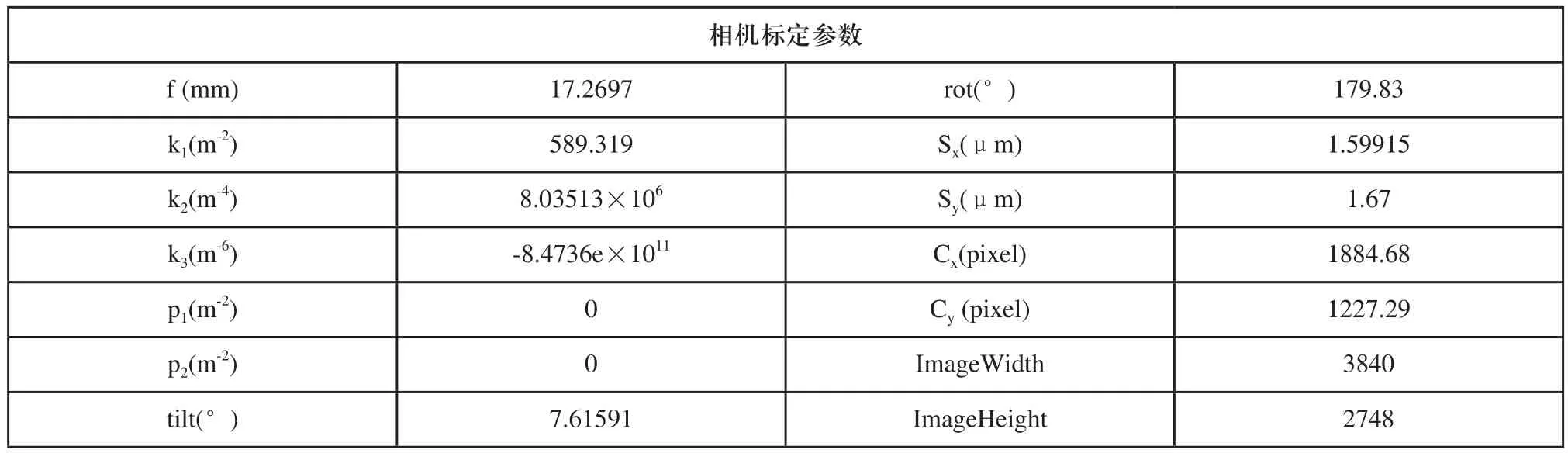
表1 HALCON标定相机结果
【】【】
根据上述要求,使用HALCON标定助手,拍摄如图7所示图片,并在标定过程中不勾选切向畸变的参数,以最后一幅图像为参考位姿,得到相机的标定结果如表1所示。标定的平均误差约为0.357368个像素。本系统硬件设计的光敏元件与透镜之间的理论夹角为6°,标定的结果为7.61591°,是相对接近的,而且标定的平均误差较小,说明标定结果可以使用。
至此,对于包含倾斜镜头的摄像机标定也有了一般的方法,有助于Scheimpflug定律在激光三角测量系统中的应用,有助于提高系统的精度。
4 结束语
激光三角测量法的应用虽然较多,但是沙姆定律的应用却不多,主要一部分原因是倾斜镜头的标定还没有流程化的步骤,鲜有学者对倾斜镜头的标定做深入的研究,本文发现了HALCON机器视觉软件可用来标定倾斜镜头,并对包含的模型进行了深入的学习,才建立了本文倾斜镜头的摄像机数学模型,倾斜镜头的摄像机标定也因此有了流程化的步骤,这对未来沙姆定律在三维测量系统中的应用有重要作用。
[1]周富强,张广军.表面视觉传感器模型参数的简易标定方法[J].机械工程学报,2005.41(3):175-179.
[2]陈新禹,马孜,陈天飞.线结构光传感器模型的简易标定[J].光学精密工程,2012.20(11):2345-2352.
[3]唐朝伟,梁锡昌,邹昌平.三维曲面激光精密测量技术[J].计量学报,1994.15(2):65-69.
[4]吴文琪,孙增圻.机器视觉中的摄像机定标方法综述[J].计算机应用研究,2004(2):4-6.
[5]谭晓波.摄像机标定及相关技术研究[D].长沙:国防科技大学,2004.
[6]张铖伟,王彪,徐贵力.摄像机标定方法研究[J].计算机技术与发展,2010.20(11):175-176.
[7]于仕琪,刘瑞祯.学习OpenCV中文版[M].北京:清华大学出版社,2009.
