商用航空发动机稳态控制误差分析方法研究
2018-01-18
(中国航发商用航空发动机有限责任公司,上海 201108)
0 引言
航空发动机控制系统设计中,稳态控制误差是系统的重要性能指标,被控量包括高压转子转速(N2)、高压压气机可调静子叶片(VSV)角度等。在进行系统设计时,要根据调节计划和稳态控制误差要求,将控制误差分配到控制回路的各个误差环节。若根据现有技术水平,各环节误差合成后无法满足控制回路误差要求,则需要改变调节计划、降低回路误差要求,或者提高各误差项的精度,这是一个迭代的过程。其中,误差项的确定及合成是其中的关键。
现有的闭环稳态控制误差分析存在理论分析与实际不对应的问题,理论计算结果难以支撑系统验证。因此,需对闭环回路误差模型做进一步分析,优化误差合成算法。
本文提出一种考虑随机误差的闭环稳态控制误差分析合成方法,对误差项的误差传递系数进行了近似推导,从而使得误差合成结果更加贴近实际情况。通过系统全数字仿真以及半物理试验,证明本文方法正确有效。
以N2控制回路为例,第1章对回路进行建模,明确回路中的各误差项;第2章介绍了现有的两种误差分析方法及其存在的问题;第3章提出了考虑误差传递系数的误差分析方法;第4章是对第3章提出算法的仿真及验证;第5章是全文小结。
1 控制回路建模
1.1 误差由来
稳态下对于输出量的期望值与输出量的实际值之间的差,称为稳态误差或静态误差。根据相关自控原理,对于开环传递函数中含有积分环节的系统(1型以上系统),在阶跃输入信号作用下没有静差,称作无静差系统[1]。
发动机的控制回路中通常含有积分环节,因此在理论上是无静差系统。以N2控制回路为例,该回路为内外双环结构,外环为转速控制闭环,内环为燃油计量控制闭环,内外环中PI控制器均含有积分环节,因此理论上内外环稳态控制误差均为0,即N2稳态误差为0。
但实际控制回路中各环节均存在误差,因此在稳态时总会存在误差。误差分析的目的,就是在系统设计阶段提前预估系统稳态误差,尽量从设计角度满足系统性能指标。
1.2 回路建模
在误差分析时,应首先搞清回路中误差项的来源。对N2控制回路建模如图1所示,其中虚框部分是燃油计量小闭环,如图2所示。
对于图1的N2控制回路,误差来源包括:传感器误差、控制器A/D转换误差、控制器D/A转换误差、计量活门标定误差、伺服油压波动误差等。根据注入位置将误差归并为以下误差项:
1)ΔPLA:PLA信号误差,包括传感器误差ΔPLAsensor与A/D转换误差ΔPLAAD;
2)ΔT25:T25信号误差,包括传感器误差ΔT25_sensor与A/D转换误差ΔT25_AD;
3)ΔN2:N2反馈信号误差,包括N2传感器误差ΔN2_sensor与F/D转换误差ΔN2_FD;
4)ΔWf:计量燃油流量误差,包括(各误差项如图2所示)。
(1)计量活门位置解算器误差与A/D转换误差ΔLfmv_f;
(2)D/A转换误差ΔIfmv;
(3)计量活门标定及伺服油压波动造成的计量活门位置给定误差ΔLfmv_d。
N2控制回路的各环节近似线性传递函数如下:
PI控制器:
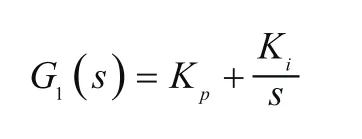
燃油计量环节:
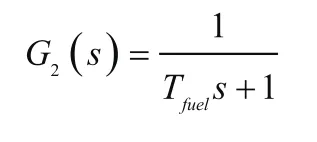
发动机模型:
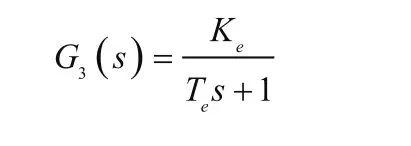
信号滤波:
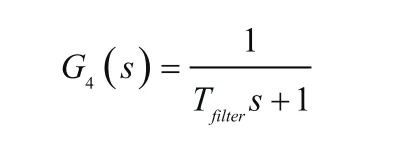
图中,PLAtrue、T25_true代表PLA、T25信号的真值,相应地,代表N2给定值的真值。
2 研究现状
2.1 方法介绍
2.1.1 方法一
该方法[2~4]考察N2给定值真值与N2输出值之间的误差,即且假设各误差项ΔPLA、ΔT25、ΔN2_f、ΔWf为系统误差。
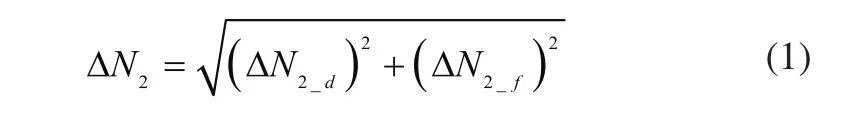
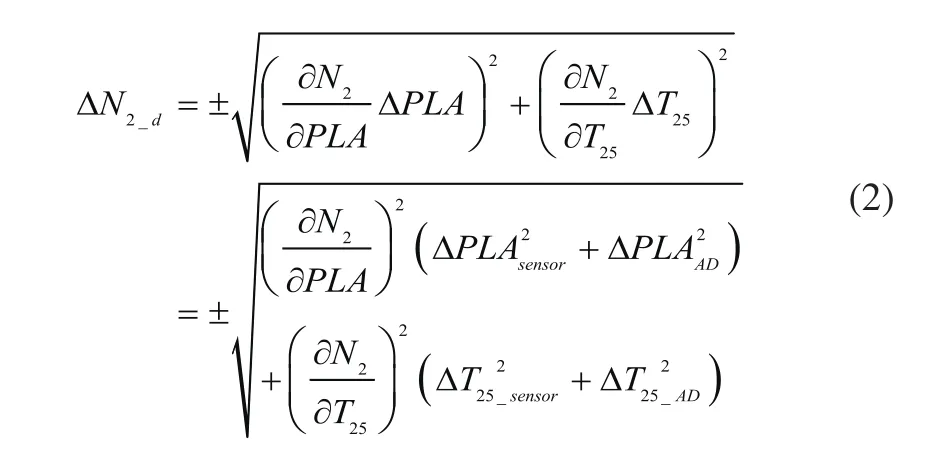
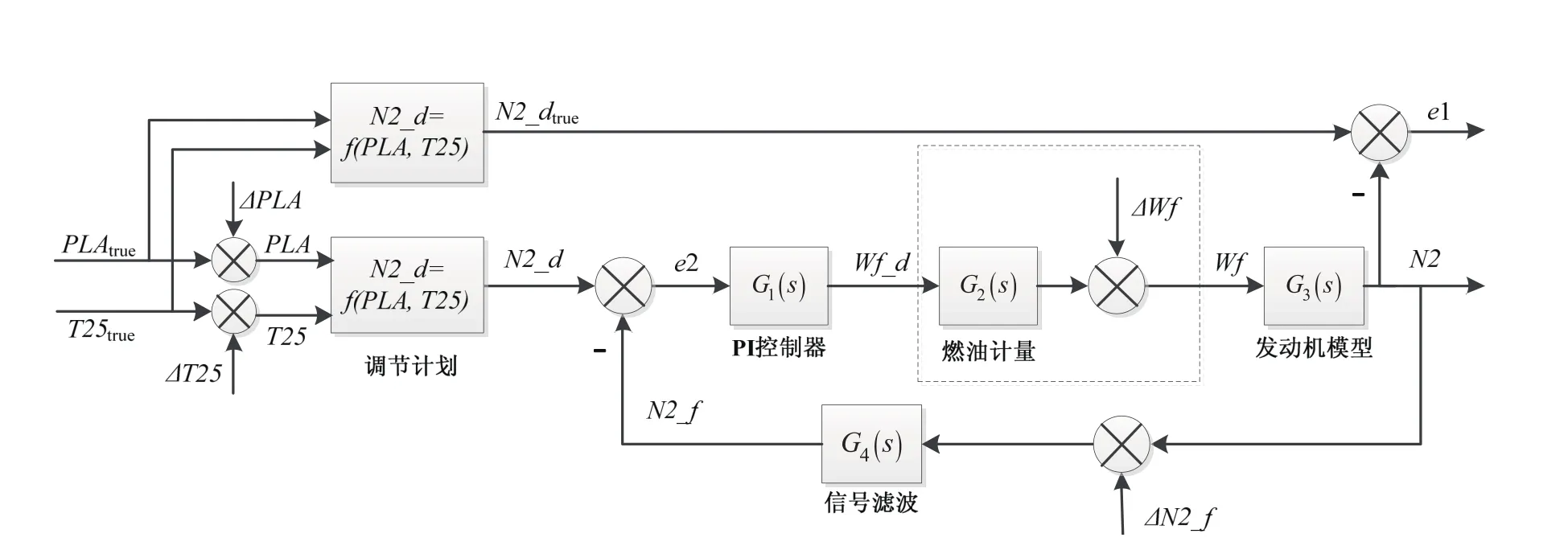
图1 N2控制回路示意图

图2 燃油计量控制回路示意图
N2反馈误差亦由传感器误差和转换误差两部分组成,即:

将式(2)、式(3)代入式(1)即可。
2.1.2 方法二
该方法[5]考察的误差为且假设误差项均为随机误差,所有误差传递系数为1,则:
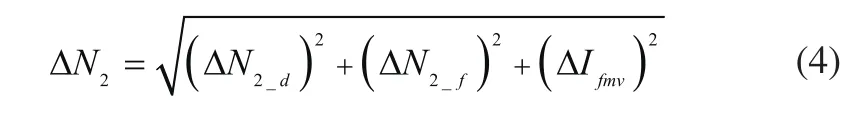
ΔN2_d和ΔN2_f参照式(2)、式(3)计算。
2.2 当前方法分析
2.2.1 方法一
该误差合成方法只合成了给定误差ΔN2_d和反馈误差ΔN2_f,而忽略了回路中的燃油流量误差项ΔWf,原因在于假设误差项为系统误差,在这种情况下,积分环节(PI控制器G1(s))后的燃油流量误差项ΔWf对总误差e1不产生影响。
图1中:
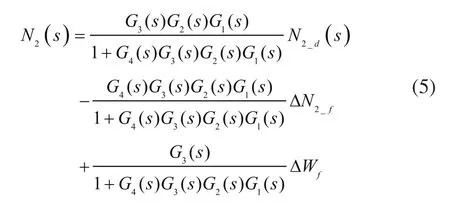
因为ΔPLA、ΔT25、ΔN2_f、ΔWf为不随时间变化的常数,将G1(s)~G4(s)依次代入,当系统处于稳态时:
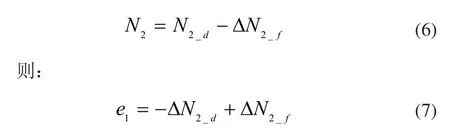
从而,回路控制误差e1由给定误差ΔN2_d和反馈误差ΔN2_f两部分构成。
在误差合成时,将各误差项看成是未定系统误差,参照随机误差的合成方法进行合成。
从误差的大小来看,各环节的误差项可看成是各测量值的极限误差,N2回路误差ΔN2可用e1的极限误差表征,即:

在实际研制中,通常不直接对e1进行考察,因为真实的给定值和反馈值都难以获取,所以实际通常考察的误差为其中:
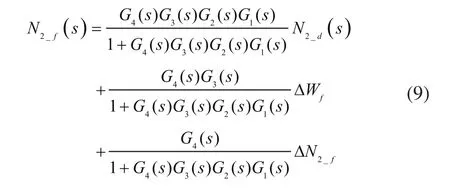
若仍假设ΔPLA、ΔT25、ΔN2_f、ΔWf为系统误差,即ΔPLA、ΔT25、ΔN2_f、ΔWf为不随时间变化的常数,将G1(s)~G4(s)依次代入,当系统处于稳态时:
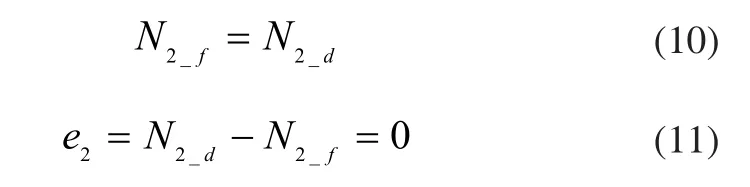
从而:
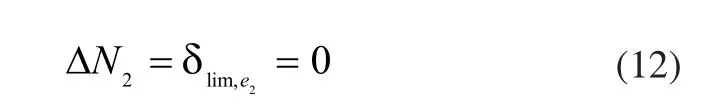
即若考察误差e2,则ΔPLA、ΔT25、ΔN2_f、ΔWf这些系统误差均不对其产生影响。但实际上,显然ΔN2>0,从而理论计算结果与实际不符。
2.2.2 方法二
该方法假设各误差项为随机误差,因此将外环积分环节(PI控制器G1(s))后的燃油计量闭环中控制器D/A转换误差ΔIfmv包含在被合成的误差项中。
该方法的问题在于,对燃油计量环节的误差考虑不够,只计算了其中D/A转换产生的误差ΔIfmv,而实际上ΔWf还包括计量活门位置给定误差ΔLfmv_d和计量活门位置反馈误差ΔLfmv_f,且因为伺服油压波动、计量活门标定误差等因素,最主要的部分是计量活门位置给定误差ΔLfmv_d。一般而言,合成后的燃油计量误差ΔWf通常远大于N2回路的误差ΔN2。此时若直接在式(4)中将ΔIfmv替换为ΔWf,合成后的误差ΔN2将大大超出N2回路误差要求。
2.3 小结
当前两种方法是基于不同的闭环控制回路误差模型建立的误差合成方法,但两种方法都存在一定的问题。
若采用方法一,该方法假设各误差项均为系统误差,考察的是理想的误差e1;但对于实际考察的误差e2,根据理论分析ΔN2=0,与实际误差ΔN2不为0矛盾,即实际误差ΔN2来源在该误差模型下无法给出合理的解释;
若采用方法二,该方法考察的误差为e2,与实际一致,假设各误差项均为随机误差,且假设所有误差传递系数为1,但少算了误差项ΔWf中的一大部分,若加入该部分误差,则合成误差将远大于N2转速回路的误差要求。
综上,方法二的误差模型与实际更为接近,但需对各误差项的误差传递系数进行研究,使得理论计算值尽量符合实际情况。
3 考虑误差传递系数的控制误差分析方法
对图1中的燃油计量、发动机模型以及传感器滤波环节进行线性化处理,得到图3,其中:
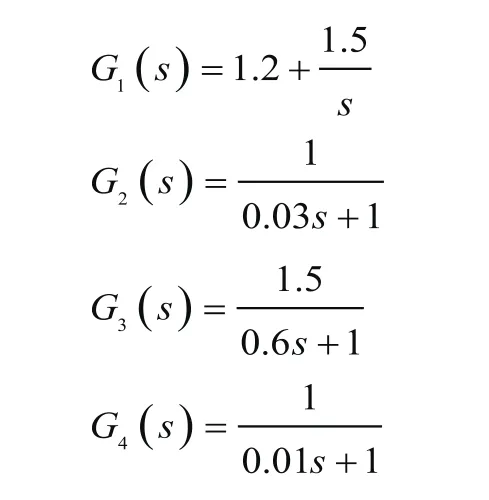
图中为简洁起见,将ΔPLA、ΔT25合并为ΔN2_d,从而N2控制误差ΔN2主要来自三个环节:给定值误差ΔN2_d、计量燃油流量误差ΔWf、N2反馈信号的误差ΔN2_f。令回路误差需要分析和计算各个误差对ΔN2的影响。
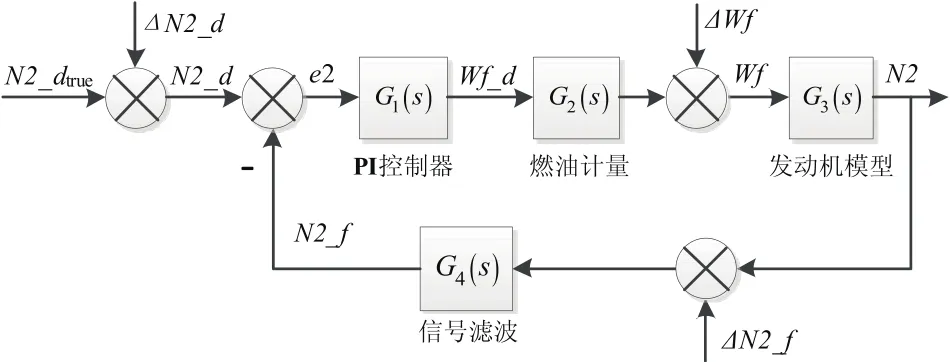
图3 N2控制回路示意图(合并误差项后)
假设这些误差均为服从正态分布的随机量,即:
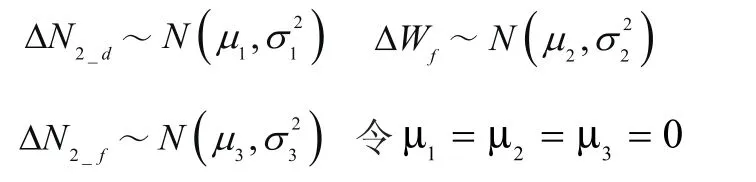
根据线性原理,反馈量N2_f也是服从正态分布的随机量,。因回路误差:
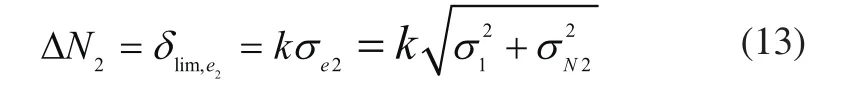
其中,k为极限误差的置信系数,通常取值范围为2~3,本文中统一取值为3。因此问题即为根据σ1、σ2、σ3计算σN2。
3.1 单个误差分析
此处以ΔN2_d为例,分析N2_d处加入随机误差ΔN2_d后对N2_f的影响。即令σ2=σ3=0,根据σ1计算σN2。设N2控制回路运行周期为Ts=0.02s。
1)设ΔN2_d0(t)为宽度为Ts=0.02s的脉冲(如图4(a)所示),即:

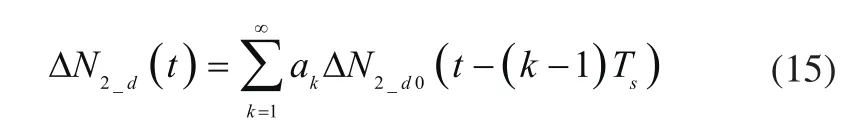
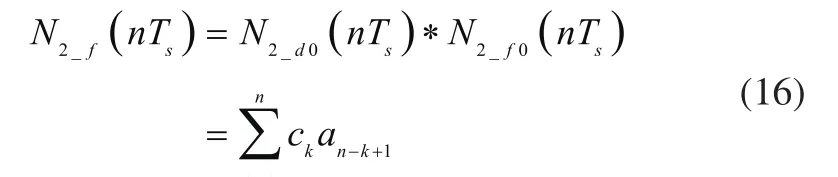
从而:
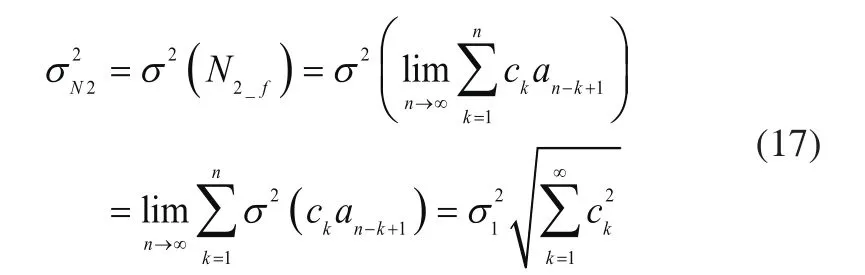
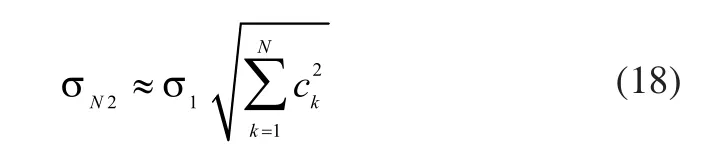
N2_d和N2_f在某次运行后的结果如图5所示,可见给定处的误差ΔN2_d经过回路的传递,在N2_f处误差幅值变小,振荡变缓。因此针对方法二存在的问题就能给出合理的解释,即燃油计量环节误差确实存在,且幅值远大于回路误差,但经过回路的衰减,在N2_f处误差幅值变小,符合实际情况。
3.2 多误差合成
一般地,设闭环中有q个单项随机误差,各单项随机误差的标准差为σi,相应的误差传递系数为αi,第i和j个误差的相关系数为ρij,则合成的闭环反馈量y的标准差为:
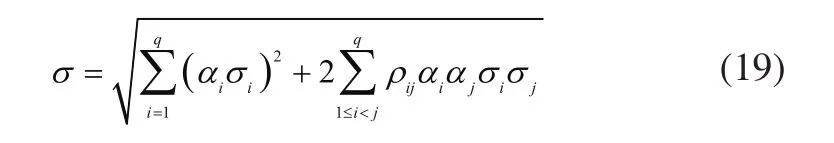
对于误差传递系数αi,可在第i个随机误差处注入宽度为Ts的脉冲记录反馈值各周期的值从而:
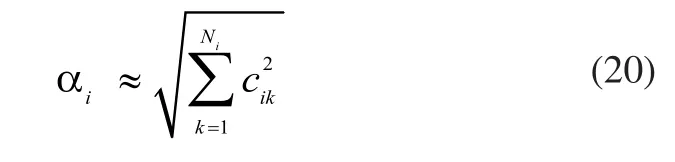
一般情况下各个误差互不相关,ρij=0,则:
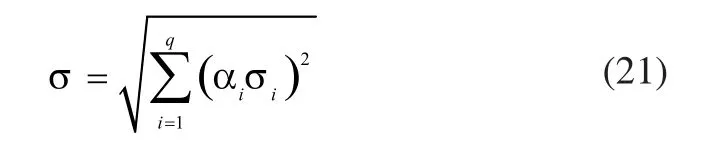
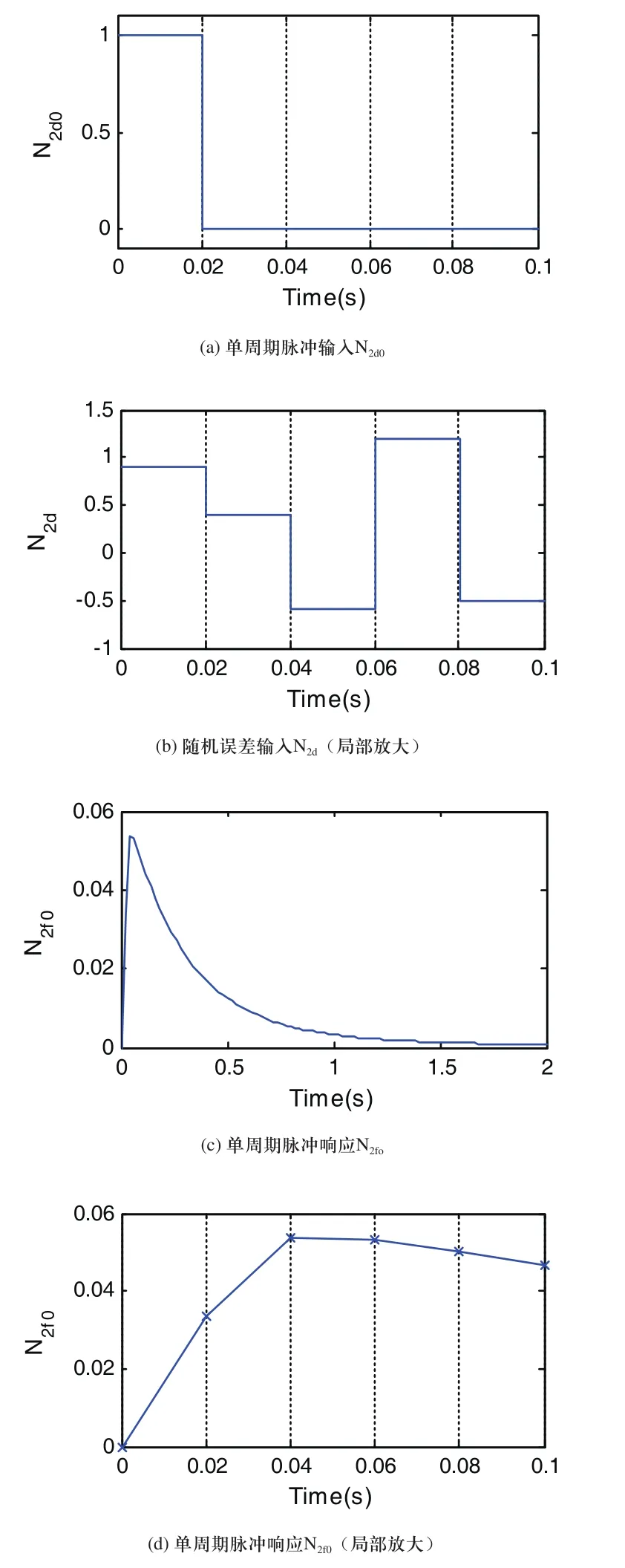
图4 单个误差分析输入、输出图示
在实际中,通常误差项和合成结果均以极限误差的形式表示。设各单项极限误差分别为记闭环反馈量y的极限误差为从而:
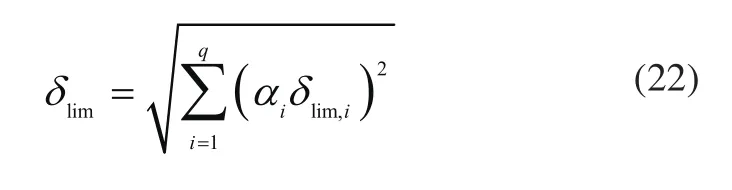
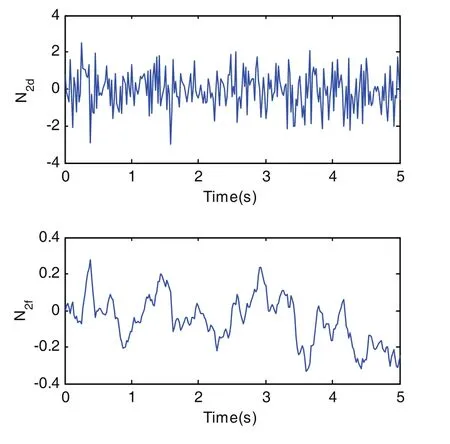
图5 随机误差输入N2_d和响应N2_f
对于图3的回路,ΔN2_d、ΔWf、ΔN2_f三者共同作用,三者之间互不相关,可得N2_f标准差为:
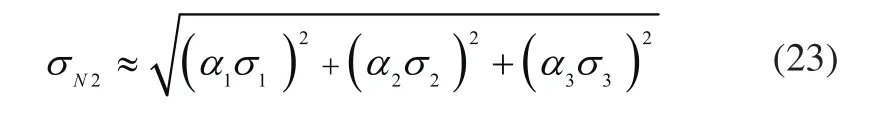
与上文类似,各误差项ΔN2_d、ΔWf、ΔN2_f可看成是测量值的极限误差,从而回路误差ΔN2为:
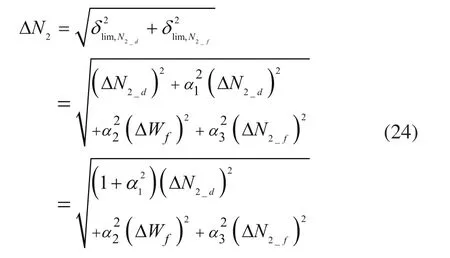
4 误差分析方法仿真及试验验证
4.1 全数字仿真
下面对于第3章提出的算法进行全数字仿真验证。对于图3的回路,分别设置随机误差ΔN2_d、ΔWf、ΔN2_f的方差,取运行周期为Ts=0.02s,运行时长T=5000s,读取误差e2的标准差,根据式(13)计算结果作为绝对误差ΔN2实测值,并根据式(24)算出计算值。相对误差(相对于100%N2值)δN2为全数字仿真验证结果如表1所示。
全数字仿真结果表明误差合成算法正确有效,ΔN2误差最大不超过0.1%,δN2误差可忽略不计。
4.2 半物理试验
根据稳态半物理试验数据,读取ΔN2_d、ΔWf、ΔN2_f处的方差,计算N2反馈值的标准差σN2、绝对误差ΔN2、相对于100% N2值的N2稳态控制误差δN2,并与实测值进行对比,结果如表2所示。根据结果可知,绝对误差ΔN2相差约20%,δN2误差不超过0.02%。因半物理环境中误差项较理论情况多,因此实际值比计算值略大较为合理。
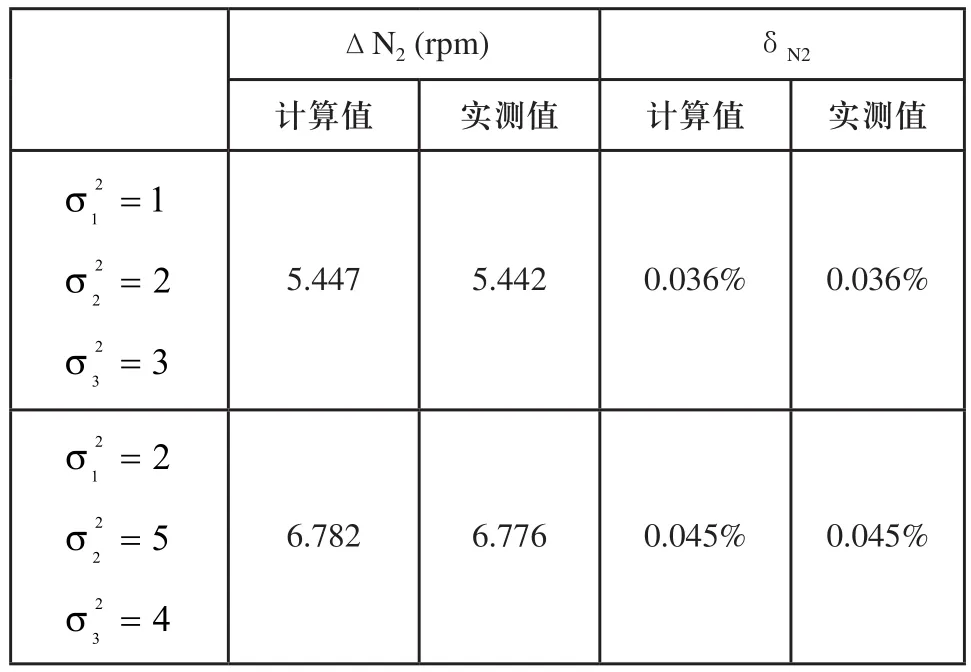
表1 全数字仿真结果
5 结论
本文针对商用航空发动机稳态下控制回路的误差分析问题,分析了现有两种误差分析方法存在的问题,提出了一种闭环控制随机误差的合成方法,该方法给出了误差项的误差传递系数的近似算法。通过系统全数字仿真证明误差合成算法正确有效。由于回路各环节的线性化近似、误差项的波动特性偏差、误差项与实际情况不完全一致等因素,误差合成计算结果与半物理试验结果还有一定的差距,后续应对误差项的来源和性质做进一步的梳理和研究,从而更好地用理论指导实际工作。
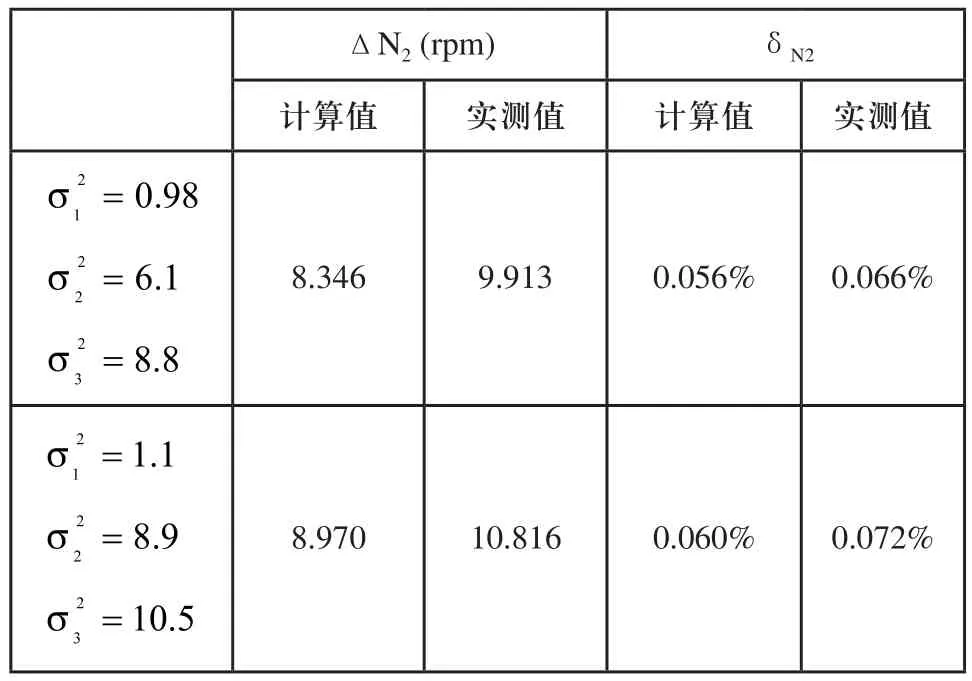
表2 半物理试验结果
[1]吴麒,王诗宓.自动控制原理[M].2版.北京:清华大学出版社,2006.
[2]钱政,王中宇,刘桂礼.测试误差分析与数据处理[M].北京:北京航空航天大学出版社,2008.
[3]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2004.
[4]殷锴,陶金伟,王鸿钧,等.民用航空发动机控制系统回路设计与仿真[J].航空计算技术,2012,42(6):107-110.
[5]姚华.航空发动机全权限数字电子控制系统[M].北京:航空工业出版社,2014.
