发动机台架试验特性曲线拟合算法研究与实现
2018-01-18尹宪栋谢中朝
杨 扬,尹宪栋,谢中朝
(1.武汉理工大学 自动化学院,武汉430070;2.中国地质大学(武汉)自动化学院,武汉430074)
发动机台架试验是发动机性能测试的主要方法[1],目的是尽量模拟发动机实际运转时的各种工况,精确测量发动机的性能指标,获得发动机的试验特性曲线,以研究发动机性能[2]。发动机特性主要包括外特性和负荷特性[3]。通过研究发动机特性曲线,衡量发动机的最高动力性能,确定发动机在不同负荷和不同转速时的燃油经济性及最有利的工作转速范围[4]。
本文以某型号柴油发动机为例,设计发动机台架试验数据采集系统,研究发动机外特性和负荷特性曲线拟合算法及程序实现,精确绘制特性曲线,并保证曲线光滑且符合实际。对比几种曲线拟合算法,建立适合处理发动机外特性和负荷特性试验数据的算法模型,用C++编写算法程序,实现发动机特性曲线绘制,为绘制发动机万有特性曲线提供依据,为发动机性能分析提供准确基础[5]。
1 发动机台架试验数据采集
1.1 发动机特性
发动机外特性曲线是指在发动机全负荷(汽油机为节气门全开)时测得的功率或扭矩随转速变化的曲线[6]。当燃料供给机构位置达到最大时,得到的是总功率特性,也称发动机外特性。发动机的外特性是衡量发动机具有的最高动力性能的依据[7]。
发动机的负荷特性是指当发动机转速一定时,有效比燃油消耗量随发动机负荷的变化关系。利用发动机的负荷特性曲线,可以全面地确定发动机在不同负荷和转速时的燃油经济性[8]。
1.2 试验数据采集系统
发动机台架试验数据采集系统结构如图1所示,采用CAN总线完成数据采集。工控机采集发动机台架试验过程的燃油消耗率、油耗量、温度和压力等参数,并存储在文件中,能够进行数据处理、试验特性曲线绘制和实时参数显示等。STM32作为下位机,负责测量励磁、油门、转速和扭矩,再通过CAN总线传送给工控机。

图1 发动机台架试验数据采集系统Fig.1 Engine bench test data acquisition system
在发动机油门全开时,测量转速与扭矩,获得如表1所示的14组外特性试验数据。采集负荷特性试验数据的方法为在50%~80%的额定转速下,保持发动机转速不变,从小负荷开始,逐步加大油门开度直至全负荷,适当分布8个以上测量点,获得发动机功率、燃油消耗率和油耗量。表2所示为发动机转速为2400 r/min时测量的9组负荷特性试验数据。

表1 外特性试验数据Tab.1 Test data of external characteristics

表2 负荷特性试验数据Tab.2 Test data of load characteristics
2 曲线拟合算法
为了通过有限的试验数据精准拟合出光滑的曲线,必须采取插值或拟合算法进行函数逼近。常用的曲线拟合算法有最小二乘法、多项式拟合、三次样条插值算法和折线法等。采用折线法绘制的发动机负荷特性曲线不光滑,无法真实反映变化规律。
2.1 最小二乘法多项式拟合
运用多元线性回归理论进行多项式曲线拟合,给定数据点(xi,yi)(i=0,1,2,…,N),利用多项式(1)拟合出x与y的关系曲线,拟合的原则是使式(2)所示的偏差的平方和最小[9]。
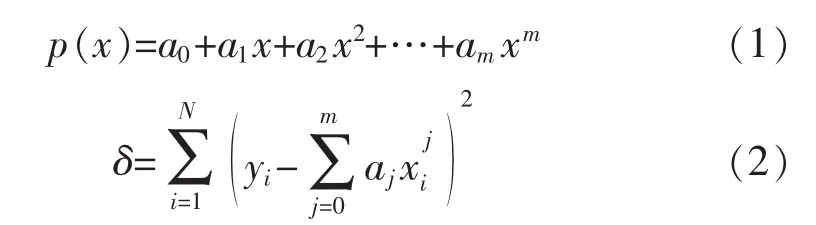
以二次多项式拟合为例,多项式函数拟合的法方程如式(3)所示,求解法方程,得到二次多项式的系数,从而求得二次多项式函数。

本文采用最小二乘法多项式拟合绘制发动机外特性曲线,曲线与试验数据点的偏差平方和最小,且能够通过试验数据点之间。
2.2 三次样条插值算法
由于发动机负荷特性曲线连续一阶可导,具有二阶导数且二阶导数不为零,因此,由试验数据拟合的曲线也必须一阶、二阶可导。同时,要求曲线与试验数据点间的偏差最小,曲线通过试验数据点。因此,本文采用三次样条插值算法绘制发动机负荷特性曲线。
三次样条插值可以使插值函数既是低阶分段函数,又是光滑的函数。给定区间[a,b]上的一个划分:a=x0 给定 n+1 个数据节点(x0,y0),(x1,y1),(x2,y2),…,(xn,yn),则三次样条插值函数的求解方法为①计算步长 hi=xi+1-xi(i=0,1,…,n-1);②确定边界条件下首尾端点条件,本设计中采用自然边界,首尾端点的二次微分值满足式(5); ③由数据节点和首尾端点条件得到式(6)所示的矩阵方程,式中 mi(i=0,1,…,n)表示各数据节点的二次微分值;④解式(6)所示的3对角矩阵方程,求解二次微分值mi;⑤依式(7)计算三次样条曲线的系数,其中 i=0,1,…,n-1; ⑥在每个子区间[xi,xi+1](i=0,1,…,n-1)上创建如式(8)所示的三次多项式方程,由此方程得出三次样条插值曲线。 用三次样条插值算法绘制的曲线不仅光滑度好,而且当节点逐渐加密时,其函数值在整体上非常逼近被插值函数,相应的导数值也收敛于被插值函数的导数,能够保证曲线一阶和二阶导数连续,不会发生龙格现象[10],拟合方法简单易行,便于编程实现。因此,本文采用三次样条插值算法绘制发动机特性曲线。 在发动机台架试验数据采集系统的上位机软件中实现拟合算法,采用C++和MFC编写试验数据处理和特性曲线绘制程序的流程如图2所示。 若选择绘制外特性曲线,则采用最小二乘法多项式拟合程序。程序步骤为①从文件中读取外特性试验数据,求得转速和扭矩的最大值和最小值,确定绘制曲线的坐标;②去掉横坐标相同的数据点,得到有效数据点;③定义数组和法方程矩阵;④求解法方程矩阵,求解多项式系数,得到多项式拟合函数;⑤设置多个等间隔样点,依样点的x坐标计算样点的y坐标值;⑥从第一个样点到最后一个样点依次画线,从而绘制出外特性曲线。 图2 特性曲线绘制程序流程Fig.2 Program flow chart of drawing characteristics curves 若绘制负荷特性曲线,则采用三次样条插值算法程序。程序步骤为①从文件中读取负荷特性试验数据,绘制坐标系;②数据处理,去掉横坐标相同的数据点,得到用于插值算法的有效数据节点;③定义数组,用于存放步长、三次样条曲线的系数、节点二次微分值等,并定义对三角矩阵;④计算步长,求解对三角矩阵,得出节点二次微分值;⑤计算三次样条曲线函数的系数,得出每个节点区间上的三次多项式方程;⑥画曲线。 调用最小二乘法多项式拟合程序绘制的外特性曲线如图3所示,曲线反映了发动机油门全开时扭矩与转速的关系,曲线光滑且准确通过试验数据点之间,与试验数据点之间的偏差平方和最小,因此,最小二乘法多项式拟合是一种比较理想的发动机外特性曲线绘制方法。 图3 最小二乘法多项式拟合外特性曲线Fig.3 External characteristics curve drew by using the least squares polynomial fitting method 调用三次样条插值算法程序和最小二乘法多项式拟合程序绘制的负荷特性曲线分别如图4和图5所示。曲线表示的是转速为2400 r/min时,燃油消耗率及油耗量与功率之间的关系。从图中可以看出,通过三次样条插值算法绘制的负荷特性曲线光滑,具有一阶和二阶连续导数,曲线精确地通过所有试验数据点,稳定性和收敛性较好,符合发动机负荷特性的实际情况;采用最小二乘法多项式拟合法绘制的曲线光滑,但是误差较大,高次多项式拟合时容易出现振动,与实际不符,不能采用。 图4 三次样条插值算法拟合负荷特性曲线Fig.4 Load characteristics curve drew by using cubic spline interpolation algorithm 图5 最小二乘法多项式拟合负荷特性曲线Fig.5 Load characteristics curve drew by using the least squares polynomial fitting method 本文设计了发动机台架试验数据采集系统,对比了几种曲线拟合算法,建立适合处理发动机外特性和负荷特性试验数据的算法模型,采用C++编写算法程序,绘制的特性曲线光滑且符合实际。采用最小二乘法多项式拟合绘制的发动机外特性曲线比较理想。针对负荷特性曲线的特点,采用三次样条插值算法绘制曲线,并与最小二乘法多项式拟合结果进行对比。结果表明,三次样条插值算法是一种比较理想的发动机负荷特性曲线绘制方法。 [1]姜鲲昌,张明.汽车整车和发动机可靠性道路试验分析[J].中国机械,2014(24):133-134. [2]王东星.基于虚拟仪器和CAN总线的发动机测控系统[D].南京:南京理工大学,2012. [3]王峰.发动机台架试验实时监测技术的研究与软件实现[D].武汉:武汉理工大学,2010. [4]赵小辉,张明柱,白东洋,等.柴油发动机特性曲线分析与建模[J].中国农机化学报,2016,37(7):112-114. [5]杨永存,辛庆伟.一种基于试验数据的发动机特性曲线拟合[J].海军航空工程学院学报,2016,31(3):312-113. [6]林学东.发动机原理[M].北京:机械工业出版社,2008:202-205. [7]任宇翔,徐璐.发动机性能试验的概论与分析[J].装备制造技术,2013(8):179-182. [8]Andrlanir,Gammaf,Ghezzilu.Numericalanalysisofintercooled and recuperated turbofan engine[J].International Journal of Turbo and Jet-Engines,2011,28(2):139-146. [9]Snow K.Topics in total least-squares adjustment within the errors-in-variablesmode:singularcofactormatricesand prior information[D].American:The ohio State University,2012. [10]Samsul A A K,Kong V P.Shape preserving interpolation using rational cubic spline[J].Research Journal of Applied Sciences,Engineering and Technology,2014,2(8):167-178.



3 拟合算法的程序实现




4 结语
